中考数学几何模型决胜88招模型53 正方形之脚拉脚模型(含解析)
文档属性
| 名称 | 中考数学几何模型决胜88招模型53 正方形之脚拉脚模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 21:18:22 | ||
图片预览



文档简介
模型53 正方形之脚拉脚模型
跟踪练习
1. 如图, 正方形ABCD中, 点E是边CD上的动点(不与点 C,D重合),以CE为边向右作正方形CEFG, 连接AF交CD于点I, 点H是AF的中点, 连接DH, CH.给出下列结论:
①△ADH≌△CDH; ②AF 平分∠DFE ; ③若BC=4 , CG=3, 则 ④若 则 其中正确的有 ( )
A.1 B.2 C.3 D.4
2. 如图1,在线段AB上取一点C(BC>AC),如果以AC,BC为边在同一侧作正方形ACDG与正方形CBEF,连接EG,取EG的中点M,连接DM, FM, DM的延长线交EF于点N.
(1)请探究DM与FM的数量关系和位置关系,并加以证明.
(2) 如图2,将正方形CBEF 绕点C顺时针旋转,使得A,C,E在同一条直线上,其余条件不变.
①∠FEC 的度数是 ,∠DCF的度数是 .
②探究(1)中的结论是否成立 并说明理由.
3. 已 知 正方形 ABCD与正方形AEFG, 正方形AEFG绕点A 旋转.
(1)当正方形AEFG 旋转至图1的位置时,连接BG ,CF,求 的值;
(2)当正方形AEFG 旋转至图2的位置时,连接CF,BE,分别取CF,BE 的中点 M,N,连接MN,试探究:MN与BE 的数量关系和位置关系,并说明理由.
中小学教育资源及组卷应用平台
模型进阶
跟踪练习
1.如图, △ABC为等边三角形, 以AB为边向△ABC外侧作△ABD,使得∠ADB=120°, 再以点 C为旋转中心,把△CBD顺时针旋转至△CAE,给出下列结论:
①D, A, E三点共线; ②△CDE为等边三角形; ③DC平分∠BDA;④DC=DB+DA.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
2.如图, 将n个边长都为1cm的正方形按如图所示摆放,点A ,A ,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 .
3.如图, 在正方形ABCD中,O为对角线AC, BD的交点, E, F分别为边BC, CD上一点, 且OE⊥OF, 连接EF. 若∠AOE=150°,DF= 求EF的长.
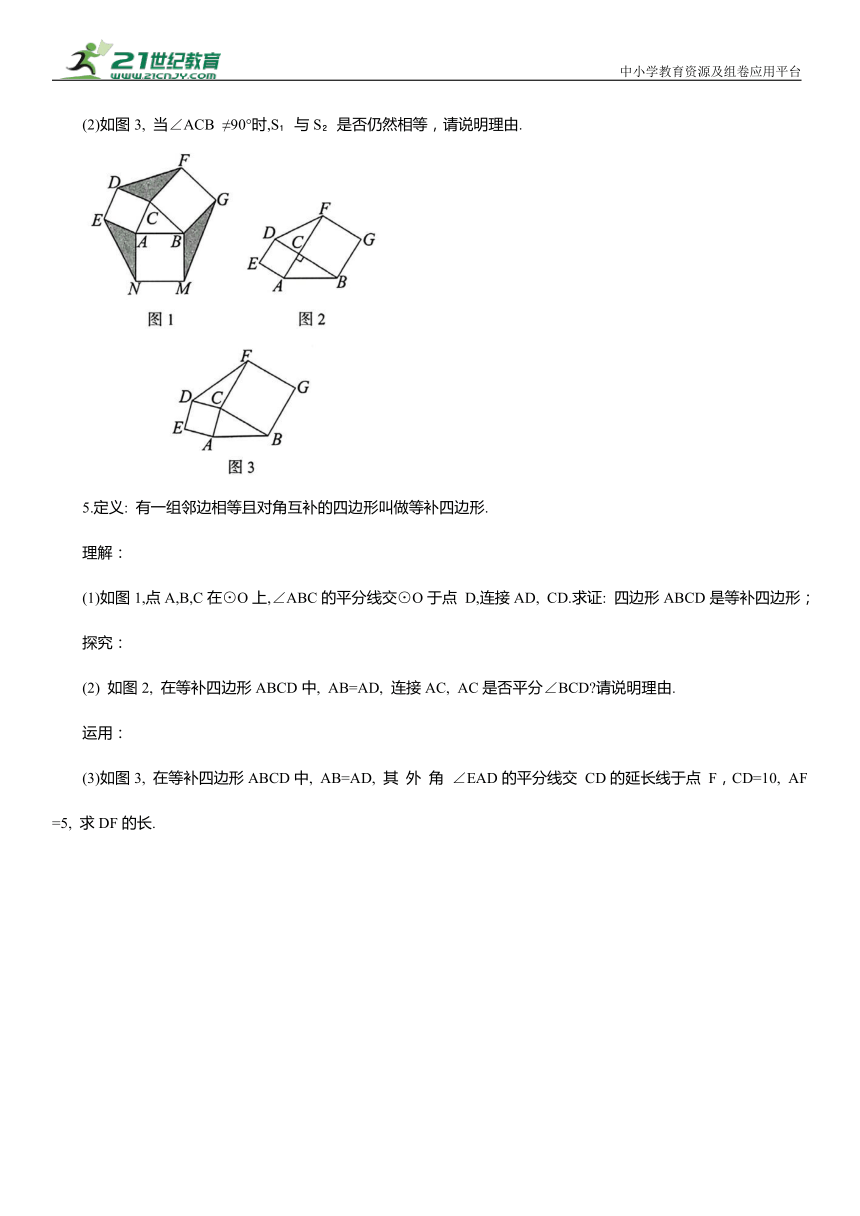
4.定义: 如图1, 若分别以△ABC的三边AC,BC,AB为边向三角形外 侧作 正方 形 ACDE, BCFG 和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形.作△ABC 的外展双叶正方形ACDE和BCFG, 记△ABC, △DCF的面积分别为S 和S .
(1) 如图2, 当∠ACB=90°时,求证:
(2)如图3, 当∠ACB ≠90°时,S 与S 是否仍然相等,请说明理由.
5.定义: 有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
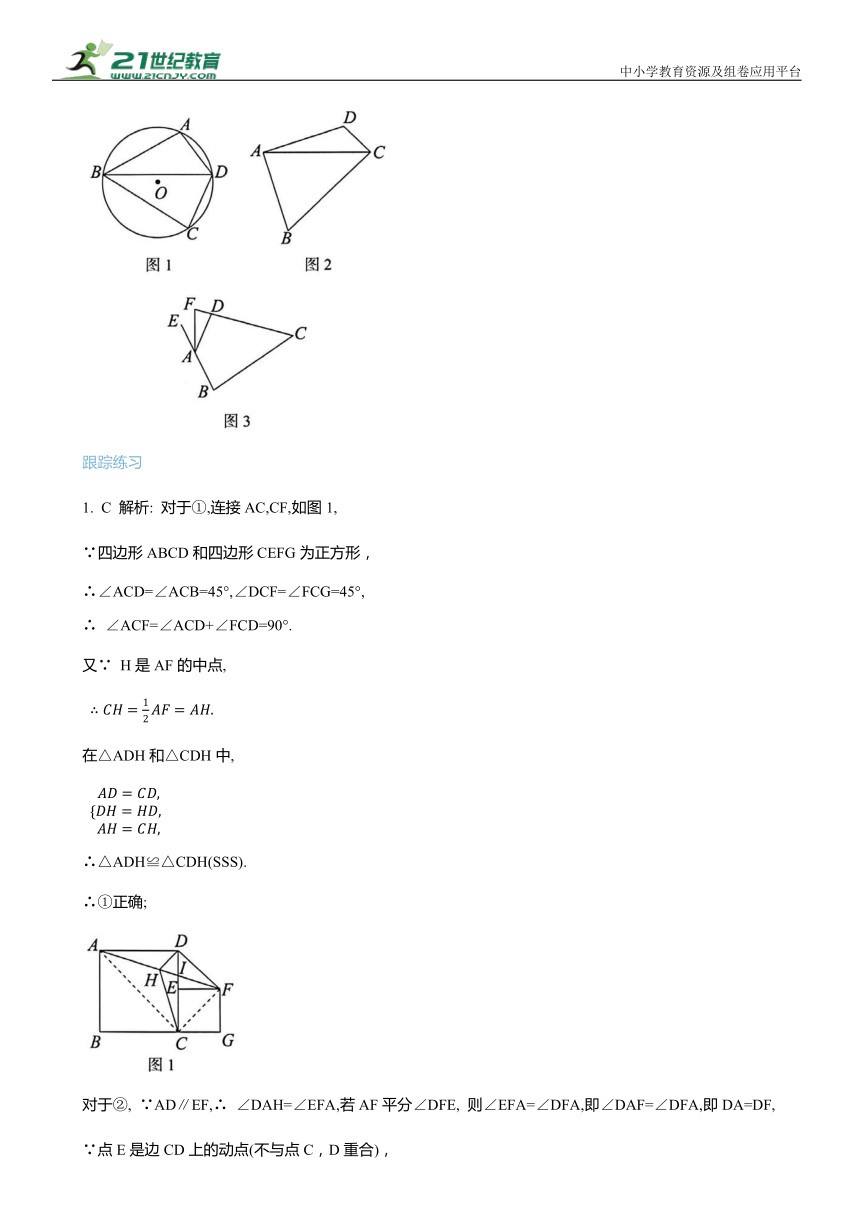
(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点 D,连接AD, CD.求证: 四边形ABCD是等补四边形;
探究:
(2) 如图2, 在等补四边形ABCD中, AB=AD, 连接AC, AC是否平分∠BCD 请说明理由.
运用:
(3)如图3, 在等补四边形ABCD中, AB=AD, 其 外 角 ∠EAD的平分线交 CD的延长线于点 F,CD=10, AF=5, 求DF的长.
跟踪练习
1. C 解析: 对于①,连接AC,CF,如图1,
∵四边形ABCD和四边形CEFG为正方形,
∴∠ACD=∠ACB=45°,∠DCF=∠FCG=45°,
∴ ∠ACF=∠ACD+∠FCD=90°.
又∵ H是AF的中点,
在△ADH和△CDH中,
∴△ADH≌△CDH(SSS).
∴①正确;
对于②, ∵AD∥EF,∴ ∠DAH=∠EFA,若AF平分∠DFE, 则∠EFA=∠DFA,即∠DAF=∠DFA,即DA=DF,
∵点E是边CD上的动点(不与点C,D重合),
∴ DA与DF 不一定相等,
∴∠DAF=∠DFA不一定成立,
∴ AF 平分∠DFE 不一定成立,
∴②不正确;
对于③,延长FE 交 AB 于点 J,如图2,
则JE=BC=AB=4,EF=CG=EC=BJ=3,
∴ FJ=EJ+EF=7, AJ=AB-BJ=4-3=1,
∴③正确;
对于④,∵AD∥EF ,∴△ADI∽△FEI .
∴④正确.
综上所述,①③④正确,故选C.
2. 解析: (1) DM=FM且DM⊥FM.
证明如下:
∵以AC, BC为边在同一侧作正方形ACDG与正方形CBEF ,
∴ EF∥GD, ∴∠NEM=∠DGM ,
∵ M为EG的中点, ∴ MG=ME,在△MGD和△MEN中,
∴△MGD≌△MEN(ASA),
∴ DM=NM, GD=NE,
∵CD=GD,
∴NE=CD, ∴ FN=FD,
∴△FDN 是等腰直角三角形,
∵ DM=NM ,
(2) ①45° 45° 提示: ∵A, C, E在同一条直线上, FE=FC, ∠CFE=90°,
∵∠DCE=90°,
②成立. 理由如下:
如图, 延长DM交CE于 N, 连接DF, FN.同(1) 可证得△MGD≌△MEN,
∴ DM=NM , NE=DG=DC,
∵∠FCE =∠FEN=45°,
∴∠DCF=∠FEN =45°.
在△DCF和△NEF中,
∴△DCF≌△NEF(SAS),
∴ DF =FN , ∠DFC=∠NFE,
∴∠DFN=∠DFC+∠CFN=∠NFE+∠CFN=90°,∴△FDN是等腰直角三角形,∵ DM=NM, ∴FM=DM=NM= DN,DM⊥FM.
3. 解析: (1)如图1, 连接AF, AC.∵四边形ABCD和四边形AEFG 都是正方形, ∠CAB=∠GAF=45°,
∴△CAF ∽△BAG,
(2) BE=2MN, MN⊥BE.
理由如下:如图2,连接ME,过点C作CH∥EF,交直线 ME于点 H,连接BH,设CF与AD的交点为P,CF与AG的交点为R,
∵ CH∥EF, ∴∠FCH=∠CFE,
∵点M 是CF的中点, ∴ CM=MF,
又∵∠CMH=∠FME,
∴△CMH≌△FME(ASA),
∴ CH=EF, ME=HM, ∴ AE=CH.
∵CH∥EF, AG∥EF,
∴CH∥AG,
∴ ∠HCF=∠CRA,
∵ AD∥BC, ∴∠BCF=∠APR,
∴∠BCH=∠BCF+∠HCF=∠APR+∠ARC,
∵ ∠DAG+∠APR+∠ARC=180°,
∠BAE+∠DAG=180°, ∴ ∠BAE=∠BCH,
又∵ BC=AB, CH=AE,
∴△BCH≌△BAE(SAS),
∴ BH=BE, ∠CBH=∠ABE,
∴ ∠HBE=∠CBA=90°,
∵ MH=ME, 点N是BE的中点,
∴ BH=2MN, MN∥BH,
∴BE=2MN, MN⊥BE.
模型进阶
跟踪练习
1. A 解析: 如图, ∵△ABC为等边三角形,∴ ∠ABC=∠BAC=∠ACB=60°, ∵ ∠ADB=120°, ∴∠1+∠2=60°, ∵以点 C 为 旋转中心把△CBD沿着顺时针方向旋转至△CAE,∴ 旋 转 角 等 于 60°, CD=CE, ∠CAE=∠CBD=∠1+∠CBA=∠1+60°, ∵∠CAE+ 即∠DAE=180°, ∴ D, A, E 三 点 共 线,∴①正确; ∵ ∠DCE=∠ACB=60°,CD=CE, ∴△CDE为等边三角形, ∴②正确; ∵△CDE为等边三角形, ∴∠3=60°,∴ ∠4=60°, ∴ DC平分∠BDA, ∴③正确;∵△CDE为等边三角形, ∴ CD=DE,∵ AE=DB, ∴ DE=DA+AE=DA+BD,∴ DC=DB+DA, ∴④正确. 故选 A.
解析:由题意可得2个正方形重叠阴影部分的面积等于正方形面积的 ,5个这样的正方形重叠部分(阴影部分)的面积和为 n个这样的正方形重叠部分(阴影部分)的面积和为
3. 解析: 在正方形ABCD中, AC和BD为对角 线, ∴ ∠AOB=∠BOC=90°, ∠OBC=∠OCD=45°, OB=OC, ∵∠AOE=150°,∴ ∠BOE=60°. ∵ OE⊥OF, ∴ ∠EOF=∠BOC=90°, ∴∠BOE=∠COF=60°,
∴△BOE ≌△COF(ASA), ∴ OE=OF,
∴△OEF 是等腰直角三角形.过点 F作FG⊥OD于点G, 如图, 则∠OGF=∠DGF=90°, ∵∠ODC=45°, ∴△DGF是等腰直角三角形, ∵ ∠BOE=60°, ∠EOF=90°,∴∠DOF=30°, ∴ OF=2GF= , ∴ EF=
4. 解析: (1) 证明: ∵四边形ACDE和BCFG都是正方形,
∴ AC=DC, BC=FC, ∠ACD=∠BCF=90°,
∵ ∠ACB=90°, ∴ ∠DCF=90°,
∴ ∠ACB=∠DCF=90°.
在△ABC和△DFC中,
∴△ABC≌△DFC(SAS).
理由如下:
如图, 过点A作AP⊥BC 于点 P, 过点D 作DQ⊥FC 交 FC 的延长线于点 Q.
∴∠APC=∠DQC=90°.
∵四边形ACDE 和四边形 BCFG均为正方形,
∴ AC=CD, BC=CF,
∵ ∠ACP+∠ACQ=90°, ∠DCQ+∠ACQ=90°.
∴∠ACP=∠DCQ.
在△APC和△DQC中,
∴△APC ≌△DQC(AAS),
∴AP=DQ.
∴BC×AP=DQ×FC,
5. 解析: (1) 证明: ∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,∠ABC+∠ADC=180°,
∵ BD平分∠ABC,
∴ ∠ABD=∠CBD,
∴AD=CD,
∴四边形ABCD是等补四边形.
(2) AC平分∠BCD, 理由如下:
如图1, 过点A分别作AE⊥BC于点E,AF⊥CD, 垂足为F,
则∠AEB=∠AFD=90°,
∵四边形ABCD 是等补四边形,
∴ ∠B+∠ADC=180°,
又∵∠ADC+∠ADF=180°,
∴∠B=∠ADF,
又∵AB=AD,
∴△ABE≌△ADF(AAS),
∴ AE=AF,
∴ AC是∠BCF 的平分线,即AC平分∠BCD.
(3)如图2, 连接AC,
∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180°,
又∵∠BAD+∠EAD=180°,
∴∠EAD=∠BCD.
∵AF平分∠EAD 由(2)知, CA平分∠BCD,
∴∠FCA=∠FAD,
又∵∠AFC=∠DFA,∴△ACF∽△DAF,
即
跟踪练习
1. 如图, 正方形ABCD中, 点E是边CD上的动点(不与点 C,D重合),以CE为边向右作正方形CEFG, 连接AF交CD于点I, 点H是AF的中点, 连接DH, CH.给出下列结论:
①△ADH≌△CDH; ②AF 平分∠DFE ; ③若BC=4 , CG=3, 则 ④若 则 其中正确的有 ( )
A.1 B.2 C.3 D.4
2. 如图1,在线段AB上取一点C(BC>AC),如果以AC,BC为边在同一侧作正方形ACDG与正方形CBEF,连接EG,取EG的中点M,连接DM, FM, DM的延长线交EF于点N.
(1)请探究DM与FM的数量关系和位置关系,并加以证明.
(2) 如图2,将正方形CBEF 绕点C顺时针旋转,使得A,C,E在同一条直线上,其余条件不变.
①∠FEC 的度数是 ,∠DCF的度数是 .
②探究(1)中的结论是否成立 并说明理由.
3. 已 知 正方形 ABCD与正方形AEFG, 正方形AEFG绕点A 旋转.
(1)当正方形AEFG 旋转至图1的位置时,连接BG ,CF,求 的值;
(2)当正方形AEFG 旋转至图2的位置时,连接CF,BE,分别取CF,BE 的中点 M,N,连接MN,试探究:MN与BE 的数量关系和位置关系,并说明理由.
中小学教育资源及组卷应用平台
模型进阶
跟踪练习
1.如图, △ABC为等边三角形, 以AB为边向△ABC外侧作△ABD,使得∠ADB=120°, 再以点 C为旋转中心,把△CBD顺时针旋转至△CAE,给出下列结论:
①D, A, E三点共线; ②△CDE为等边三角形; ③DC平分∠BDA;④DC=DB+DA.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
2.如图, 将n个边长都为1cm的正方形按如图所示摆放,点A ,A ,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 .
3.如图, 在正方形ABCD中,O为对角线AC, BD的交点, E, F分别为边BC, CD上一点, 且OE⊥OF, 连接EF. 若∠AOE=150°,DF= 求EF的长.
4.定义: 如图1, 若分别以△ABC的三边AC,BC,AB为边向三角形外 侧作 正方 形 ACDE, BCFG 和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形.作△ABC 的外展双叶正方形ACDE和BCFG, 记△ABC, △DCF的面积分别为S 和S .
(1) 如图2, 当∠ACB=90°时,求证:
(2)如图3, 当∠ACB ≠90°时,S 与S 是否仍然相等,请说明理由.
5.定义: 有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点 D,连接AD, CD.求证: 四边形ABCD是等补四边形;
探究:
(2) 如图2, 在等补四边形ABCD中, AB=AD, 连接AC, AC是否平分∠BCD 请说明理由.
运用:
(3)如图3, 在等补四边形ABCD中, AB=AD, 其 外 角 ∠EAD的平分线交 CD的延长线于点 F,CD=10, AF=5, 求DF的长.
跟踪练习
1. C 解析: 对于①,连接AC,CF,如图1,
∵四边形ABCD和四边形CEFG为正方形,
∴∠ACD=∠ACB=45°,∠DCF=∠FCG=45°,
∴ ∠ACF=∠ACD+∠FCD=90°.
又∵ H是AF的中点,
在△ADH和△CDH中,
∴△ADH≌△CDH(SSS).
∴①正确;
对于②, ∵AD∥EF,∴ ∠DAH=∠EFA,若AF平分∠DFE, 则∠EFA=∠DFA,即∠DAF=∠DFA,即DA=DF,
∵点E是边CD上的动点(不与点C,D重合),
∴ DA与DF 不一定相等,
∴∠DAF=∠DFA不一定成立,
∴ AF 平分∠DFE 不一定成立,
∴②不正确;
对于③,延长FE 交 AB 于点 J,如图2,
则JE=BC=AB=4,EF=CG=EC=BJ=3,
∴ FJ=EJ+EF=7, AJ=AB-BJ=4-3=1,
∴③正确;
对于④,∵AD∥EF ,∴△ADI∽△FEI .
∴④正确.
综上所述,①③④正确,故选C.
2. 解析: (1) DM=FM且DM⊥FM.
证明如下:
∵以AC, BC为边在同一侧作正方形ACDG与正方形CBEF ,
∴ EF∥GD, ∴∠NEM=∠DGM ,
∵ M为EG的中点, ∴ MG=ME,在△MGD和△MEN中,
∴△MGD≌△MEN(ASA),
∴ DM=NM, GD=NE,
∵CD=GD,
∴NE=CD, ∴ FN=FD,
∴△FDN 是等腰直角三角形,
∵ DM=NM ,
(2) ①45° 45° 提示: ∵A, C, E在同一条直线上, FE=FC, ∠CFE=90°,
∵∠DCE=90°,
②成立. 理由如下:
如图, 延长DM交CE于 N, 连接DF, FN.同(1) 可证得△MGD≌△MEN,
∴ DM=NM , NE=DG=DC,
∵∠FCE =∠FEN=45°,
∴∠DCF=∠FEN =45°.
在△DCF和△NEF中,
∴△DCF≌△NEF(SAS),
∴ DF =FN , ∠DFC=∠NFE,
∴∠DFN=∠DFC+∠CFN=∠NFE+∠CFN=90°,∴△FDN是等腰直角三角形,∵ DM=NM, ∴FM=DM=NM= DN,DM⊥FM.
3. 解析: (1)如图1, 连接AF, AC.∵四边形ABCD和四边形AEFG 都是正方形, ∠CAB=∠GAF=45°,
∴△CAF ∽△BAG,
(2) BE=2MN, MN⊥BE.
理由如下:如图2,连接ME,过点C作CH∥EF,交直线 ME于点 H,连接BH,设CF与AD的交点为P,CF与AG的交点为R,
∵ CH∥EF, ∴∠FCH=∠CFE,
∵点M 是CF的中点, ∴ CM=MF,
又∵∠CMH=∠FME,
∴△CMH≌△FME(ASA),
∴ CH=EF, ME=HM, ∴ AE=CH.
∵CH∥EF, AG∥EF,
∴CH∥AG,
∴ ∠HCF=∠CRA,
∵ AD∥BC, ∴∠BCF=∠APR,
∴∠BCH=∠BCF+∠HCF=∠APR+∠ARC,
∵ ∠DAG+∠APR+∠ARC=180°,
∠BAE+∠DAG=180°, ∴ ∠BAE=∠BCH,
又∵ BC=AB, CH=AE,
∴△BCH≌△BAE(SAS),
∴ BH=BE, ∠CBH=∠ABE,
∴ ∠HBE=∠CBA=90°,
∵ MH=ME, 点N是BE的中点,
∴ BH=2MN, MN∥BH,
∴BE=2MN, MN⊥BE.
模型进阶
跟踪练习
1. A 解析: 如图, ∵△ABC为等边三角形,∴ ∠ABC=∠BAC=∠ACB=60°, ∵ ∠ADB=120°, ∴∠1+∠2=60°, ∵以点 C 为 旋转中心把△CBD沿着顺时针方向旋转至△CAE,∴ 旋 转 角 等 于 60°, CD=CE, ∠CAE=∠CBD=∠1+∠CBA=∠1+60°, ∵∠CAE+ 即∠DAE=180°, ∴ D, A, E 三 点 共 线,∴①正确; ∵ ∠DCE=∠ACB=60°,CD=CE, ∴△CDE为等边三角形, ∴②正确; ∵△CDE为等边三角形, ∴∠3=60°,∴ ∠4=60°, ∴ DC平分∠BDA, ∴③正确;∵△CDE为等边三角形, ∴ CD=DE,∵ AE=DB, ∴ DE=DA+AE=DA+BD,∴ DC=DB+DA, ∴④正确. 故选 A.
解析:由题意可得2个正方形重叠阴影部分的面积等于正方形面积的 ,5个这样的正方形重叠部分(阴影部分)的面积和为 n个这样的正方形重叠部分(阴影部分)的面积和为
3. 解析: 在正方形ABCD中, AC和BD为对角 线, ∴ ∠AOB=∠BOC=90°, ∠OBC=∠OCD=45°, OB=OC, ∵∠AOE=150°,∴ ∠BOE=60°. ∵ OE⊥OF, ∴ ∠EOF=∠BOC=90°, ∴∠BOE=∠COF=60°,
∴△BOE ≌△COF(ASA), ∴ OE=OF,
∴△OEF 是等腰直角三角形.过点 F作FG⊥OD于点G, 如图, 则∠OGF=∠DGF=90°, ∵∠ODC=45°, ∴△DGF是等腰直角三角形, ∵ ∠BOE=60°, ∠EOF=90°,∴∠DOF=30°, ∴ OF=2GF= , ∴ EF=
4. 解析: (1) 证明: ∵四边形ACDE和BCFG都是正方形,
∴ AC=DC, BC=FC, ∠ACD=∠BCF=90°,
∵ ∠ACB=90°, ∴ ∠DCF=90°,
∴ ∠ACB=∠DCF=90°.
在△ABC和△DFC中,
∴△ABC≌△DFC(SAS).
理由如下:
如图, 过点A作AP⊥BC 于点 P, 过点D 作DQ⊥FC 交 FC 的延长线于点 Q.
∴∠APC=∠DQC=90°.
∵四边形ACDE 和四边形 BCFG均为正方形,
∴ AC=CD, BC=CF,
∵ ∠ACP+∠ACQ=90°, ∠DCQ+∠ACQ=90°.
∴∠ACP=∠DCQ.
在△APC和△DQC中,
∴△APC ≌△DQC(AAS),
∴AP=DQ.
∴BC×AP=DQ×FC,
5. 解析: (1) 证明: ∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,∠ABC+∠ADC=180°,
∵ BD平分∠ABC,
∴ ∠ABD=∠CBD,
∴AD=CD,
∴四边形ABCD是等补四边形.
(2) AC平分∠BCD, 理由如下:
如图1, 过点A分别作AE⊥BC于点E,AF⊥CD, 垂足为F,
则∠AEB=∠AFD=90°,
∵四边形ABCD 是等补四边形,
∴ ∠B+∠ADC=180°,
又∵∠ADC+∠ADF=180°,
∴∠B=∠ADF,
又∵AB=AD,
∴△ABE≌△ADF(AAS),
∴ AE=AF,
∴ AC是∠BCF 的平分线,即AC平分∠BCD.
(3)如图2, 连接AC,
∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180°,
又∵∠BAD+∠EAD=180°,
∴∠EAD=∠BCD.
∵AF平分∠EAD 由(2)知, CA平分∠BCD,
∴∠FCA=∠FAD,
又∵∠AFC=∠DFA,∴△ACF∽△DAF,
即
同课章节目录
