中考数学几何模型决胜88招模型35 角平分线+平行线出等腰模型(含解析)
文档属性
| 名称 | 中考数学几何模型决胜88招模型35 角平分线+平行线出等腰模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 144.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 21:25:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型35 角平分线+平行线出等腰模型
跟踪练习
1.如图, 已知 OC 平 分 ∠AOB, CD ∥ OB,若OD=3cm, 则CD等于( )
A.3cm B.4cm C.1.5cm D.2cm
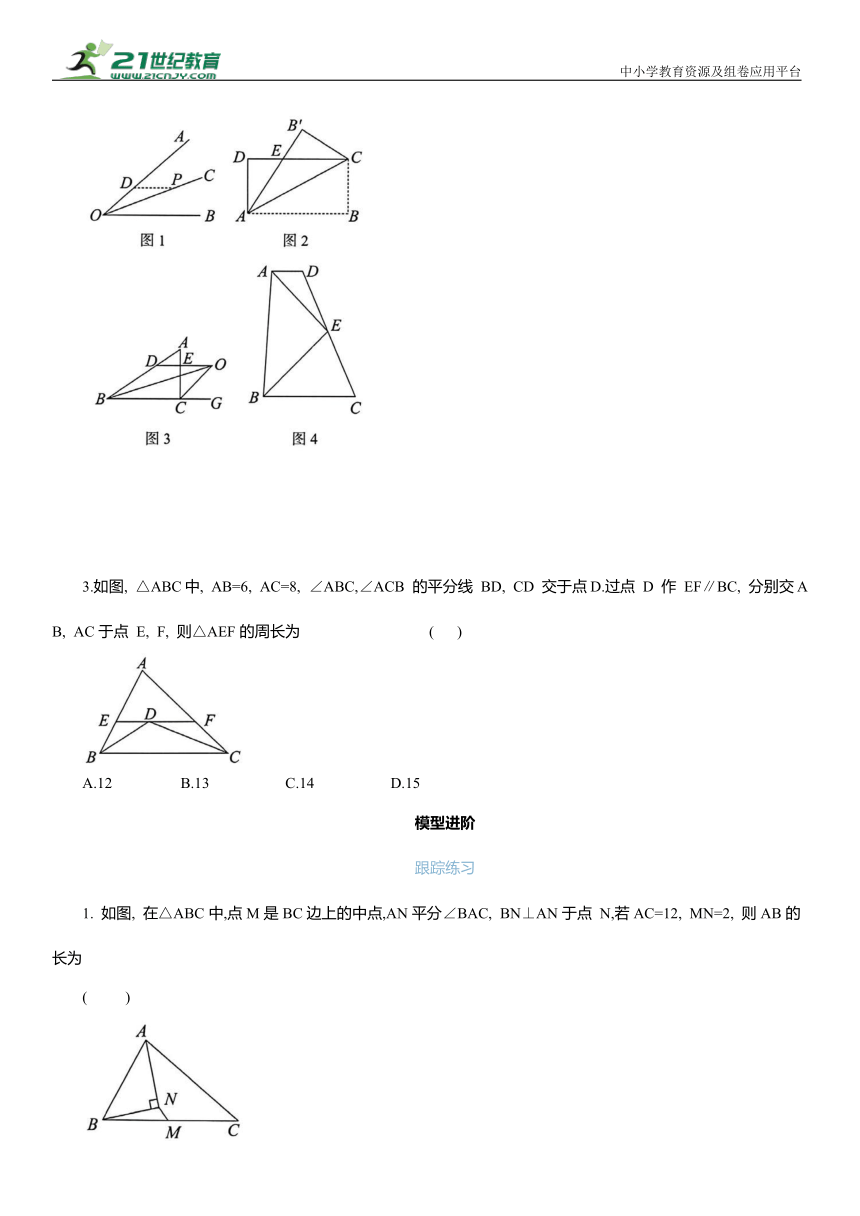
2.【问题背景】在学习了等腰三角形等有关知识后,某数学活动小组对课本上的一道例题进行了深入探究,发现:当角平分线遇上平行线时,一般可得等腰三角形,即有角平分线时,常过角平分线上一点作角的一边的平行线构造等腰三角形.如图1,P为∠AOB的平分线OC上一点,过点P作PD∥OB交OA于点 D,易证得△POD为等腰三角形.
【基本运用】如图2,把矩形纸片ABCD沿对角线AC折叠,点 B 落在点 B'处,重合部分即△ACE是等腰三角形吗 为什么
【类比探究】如图3,在△ABC中,∠ABC与外角∠ACG的平分线交于点O, 过点 O作 DE∥BC, 分别交AB, AC于点D, E, 试探究线段BD, DE, CE之间的数量关系,并说明理由.
【拓展提升】如图4,在四边形ABCD 中, AD ∥ BC, E 为 CD边的中点,且AE平分∠BAD,连接BE, 求证: AE⊥BE.
3.如图, △ABC中, AB=6, AC=8, ∠ABC,∠ACB 的平分线 BD, CD 交于点D.过点 D 作 EF∥BC, 分别交AB, AC于点 E, F, 则△AEF的周长为 ( )
A.12 B.13 C.14 D.15
模型进阶
跟踪练习
1. 如图, 在△ABC中,点M是BC边上的中点,AN平分∠BAC, BN⊥AN于点 N,若AC=12, MN=2, 则AB的长为
( )
A.4 B.6 C.7 D.8
2. 如图, 在∠MON中,以点O为圆心,任意长为半径作弧,交射线 OM 于点A,交射线 ON于点 B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点 C,作射线OC. 若OA=5, AB=6, 则点 B到AC的距离为 ( )
A.5 B. C.4 D.
3. 如图1,图2, 图3, 在△ABC中, 分别以AB, AC为边, 向△ABC外作正三角形、正四边形、正五边形,BE,CD 相交于点 O.
(1)如图1,求证:△ABE≌△ADC;
(2)探究:如图1,∠BOC= ;如图2, ∠BOC= ;如图3, ∠BOC= ;
(3) 如图4,已知:AB,AD是以AB为边向△ABC外所作正 n边形的一组邻边;AC,AE是以AC为边向△ABC外所作正n边形的一组邻边,BE,CD的延长线相交于点 O.
①猜想: 如图4, ∠BOC= (用含 n的式子表示);
②根据图4证明你的猜想.
模型35 角平分线+平行线出等腰模型
跟踪练习
1. A 解析: ∵OC平分∠AOB, ∴∠AOC=∠BOC.又∵ CD∥OB, ∴ ∠C=∠BOC,∴∠C=∠AOC,∴CD=OD=3cm,故选A.
2.解析: 【基本运用】△ACE是等腰三角形. 理由如下:
在矩形ABCD中, DC∥AB,
∴∠ACD=∠BAC,
由折叠性质可知∠B'AC=∠BAC,
∴ ∠ACD=∠B'AC, ∴ AE=CE,
∴△ACE是等腰三角形.
【类比探究】BD=DE+CE.理由如下:
∵ OB 平分∠ABC, ∴ ∠ABO=∠CBO.
∵ DE∥BC, ∴∠CBO=∠BOD,
∴ ∠ABO=∠BOD, ∴ BD=OD.
同理可得CE=OE.
又∵ OD=DE+OE, ∴ BD=DE+CE.
【拓展提升】证明:如图,延长AE,BC交于点F,
∵ AD∥BC, ∴ ∠D=∠DCF, ∠DAF=∠F.
∵ AE平分∠BAD, ∴ ∠DAF=∠BAF,
∴∠F=∠BAF,∴AB=BF.
∵ E为 CD边的中点, ∴ DE=CE.
在△ADE和△FCE中,
∴△ADE≌△FCE(AAS),
∴ AE=FE.
又∵AB=BF, ∴AE⊥BE.
3. C 解析: ∵ BD 平分∠ABC, CD平分∠ACB,∴∠ABD=∠DBC,∠ACD=∠DCB.∵ EF∥BC, ∴∠EDB=∠DBC,∠FDC=∠DCB, ∴∠ABD=∠EDB,∠ACD=∠FDC, ∴ EB=ED, FD=FC.
∵AB=6, AC=8,
∴△AEF的周长为AE+EF+AF=AE+ED+DF+AF=AE+EB+FC+AF=AB+AC=14.故选C.
模型进阶
跟踪练习
1. D
延长BN交AC于D, 证明△ANB≌△AND,根据全等三角形的性质、三角形中位线定理即可计算出AB的长.
解析:如图,延长BN交AC于 D,
∵AN平分∠BAC, ∴∠NAB=∠NAD,
又∵ AN=AN, ∠ANB=∠AND=90°,
∴△ANB≌△AND(ASA),
∴AD=AB, BN=ND,
又∵M是BC的中点,
∴ MN是△BCD的中位线,
∴ DC=2MN=4,
∵AC=AD+CD=AB+DC=12, 即AB+4=12, ∴ AB=8. 故选D.
B 解析: 由题意可得, OC为∠MON的平分线, ∵OA=OB, OC平分∠AOB,∴OC⊥AB.如图,设OC与AB交于点D,作BE⊥AC于点E, 则BE即为所求.易得AC=OA,∵AB=6, OA=5, OC⊥AB,
∴ AC=5, ∠ADC=90°, AD=3,
∴ CD=4.
解得 故选B.
3. 解析: (1) 证明: 方法一: ∵△ABD与△ACE均为等边三角形, ∴AD=AB,AC=AE, 且 ∠BAD=∠CAE=60°,∴ ∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,∴△ABE≌△ADC(SAS).
方法二: ∵△ABD与△ACE均为等边三角形, ∴AD=AB, AC=AE, 且∠BAD=∠CAE=60°,
∴可将△ADC看作由△ABE绕着点A按顺时针方向旋转60°得到,
∴△ABE≌△ADC.
(2) 120° 90° 72°
②方法一: 依题意知, ∠BAD和∠CAE都是正n边形的内角, AB=AD, AE=AC,
∴ ∠BAD-∠DAE=∠CAE-∠DAE, 即∠BAE=∠DAC, ∴△ABE≌△ADC(SAS),
∴ ∠ABE=∠ADC. ∵ ∠ADC+∠ODA=180°,
∴ ∠ABO+∠ODA=180°, ∵∠ABO+∠ODA+∠DAB+∠BOC=360°, ∴ ∠BOC+∠DAB=180°, ∴∠BOC=180°-∠DAB=180°-
方法二: 同方法一可证△ABE≌△ADC.∴ ∠ABE=∠ADC, 如图1, 延长BA交CO于 F.
∵ ∠AFD+∠ABE+∠BOC=180°, ∠AFD+∠ADC+∠DAF=180°, ∴∠BOC=∠DAF=
方法三: 同方法一可证△ABE≌△ADC.
∴ ∠ABE=∠ADC.
∠ACD)=180°-(∠ADC+∠ABC+∠ACB+∠ACD),
∠ADC+∠ACD=180°-∠DAC,
方法四: 同方法一可证△ABE≌△ADC.∴ ∠AEB=∠ACD. 如图2, 连接CE,∵ ∠BEC=∠BOC+∠OCE, ∴∠AEB+∠AEC=∠BOC+∠ACD-∠ACE, ∴∠BOC=
模型35 角平分线+平行线出等腰模型
跟踪练习
1.如图, 已知 OC 平 分 ∠AOB, CD ∥ OB,若OD=3cm, 则CD等于( )
A.3cm B.4cm C.1.5cm D.2cm
2.【问题背景】在学习了等腰三角形等有关知识后,某数学活动小组对课本上的一道例题进行了深入探究,发现:当角平分线遇上平行线时,一般可得等腰三角形,即有角平分线时,常过角平分线上一点作角的一边的平行线构造等腰三角形.如图1,P为∠AOB的平分线OC上一点,过点P作PD∥OB交OA于点 D,易证得△POD为等腰三角形.
【基本运用】如图2,把矩形纸片ABCD沿对角线AC折叠,点 B 落在点 B'处,重合部分即△ACE是等腰三角形吗 为什么
【类比探究】如图3,在△ABC中,∠ABC与外角∠ACG的平分线交于点O, 过点 O作 DE∥BC, 分别交AB, AC于点D, E, 试探究线段BD, DE, CE之间的数量关系,并说明理由.
【拓展提升】如图4,在四边形ABCD 中, AD ∥ BC, E 为 CD边的中点,且AE平分∠BAD,连接BE, 求证: AE⊥BE.
3.如图, △ABC中, AB=6, AC=8, ∠ABC,∠ACB 的平分线 BD, CD 交于点D.过点 D 作 EF∥BC, 分别交AB, AC于点 E, F, 则△AEF的周长为 ( )
A.12 B.13 C.14 D.15
模型进阶
跟踪练习
1. 如图, 在△ABC中,点M是BC边上的中点,AN平分∠BAC, BN⊥AN于点 N,若AC=12, MN=2, 则AB的长为
( )
A.4 B.6 C.7 D.8
2. 如图, 在∠MON中,以点O为圆心,任意长为半径作弧,交射线 OM 于点A,交射线 ON于点 B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点 C,作射线OC. 若OA=5, AB=6, 则点 B到AC的距离为 ( )
A.5 B. C.4 D.
3. 如图1,图2, 图3, 在△ABC中, 分别以AB, AC为边, 向△ABC外作正三角形、正四边形、正五边形,BE,CD 相交于点 O.
(1)如图1,求证:△ABE≌△ADC;
(2)探究:如图1,∠BOC= ;如图2, ∠BOC= ;如图3, ∠BOC= ;
(3) 如图4,已知:AB,AD是以AB为边向△ABC外所作正 n边形的一组邻边;AC,AE是以AC为边向△ABC外所作正n边形的一组邻边,BE,CD的延长线相交于点 O.
①猜想: 如图4, ∠BOC= (用含 n的式子表示);
②根据图4证明你的猜想.
模型35 角平分线+平行线出等腰模型
跟踪练习
1. A 解析: ∵OC平分∠AOB, ∴∠AOC=∠BOC.又∵ CD∥OB, ∴ ∠C=∠BOC,∴∠C=∠AOC,∴CD=OD=3cm,故选A.
2.解析: 【基本运用】△ACE是等腰三角形. 理由如下:
在矩形ABCD中, DC∥AB,
∴∠ACD=∠BAC,
由折叠性质可知∠B'AC=∠BAC,
∴ ∠ACD=∠B'AC, ∴ AE=CE,
∴△ACE是等腰三角形.
【类比探究】BD=DE+CE.理由如下:
∵ OB 平分∠ABC, ∴ ∠ABO=∠CBO.
∵ DE∥BC, ∴∠CBO=∠BOD,
∴ ∠ABO=∠BOD, ∴ BD=OD.
同理可得CE=OE.
又∵ OD=DE+OE, ∴ BD=DE+CE.
【拓展提升】证明:如图,延长AE,BC交于点F,
∵ AD∥BC, ∴ ∠D=∠DCF, ∠DAF=∠F.
∵ AE平分∠BAD, ∴ ∠DAF=∠BAF,
∴∠F=∠BAF,∴AB=BF.
∵ E为 CD边的中点, ∴ DE=CE.
在△ADE和△FCE中,
∴△ADE≌△FCE(AAS),
∴ AE=FE.
又∵AB=BF, ∴AE⊥BE.
3. C 解析: ∵ BD 平分∠ABC, CD平分∠ACB,∴∠ABD=∠DBC,∠ACD=∠DCB.∵ EF∥BC, ∴∠EDB=∠DBC,∠FDC=∠DCB, ∴∠ABD=∠EDB,∠ACD=∠FDC, ∴ EB=ED, FD=FC.
∵AB=6, AC=8,
∴△AEF的周长为AE+EF+AF=AE+ED+DF+AF=AE+EB+FC+AF=AB+AC=14.故选C.
模型进阶
跟踪练习
1. D
延长BN交AC于D, 证明△ANB≌△AND,根据全等三角形的性质、三角形中位线定理即可计算出AB的长.
解析:如图,延长BN交AC于 D,
∵AN平分∠BAC, ∴∠NAB=∠NAD,
又∵ AN=AN, ∠ANB=∠AND=90°,
∴△ANB≌△AND(ASA),
∴AD=AB, BN=ND,
又∵M是BC的中点,
∴ MN是△BCD的中位线,
∴ DC=2MN=4,
∵AC=AD+CD=AB+DC=12, 即AB+4=12, ∴ AB=8. 故选D.
B 解析: 由题意可得, OC为∠MON的平分线, ∵OA=OB, OC平分∠AOB,∴OC⊥AB.如图,设OC与AB交于点D,作BE⊥AC于点E, 则BE即为所求.易得AC=OA,∵AB=6, OA=5, OC⊥AB,
∴ AC=5, ∠ADC=90°, AD=3,
∴ CD=4.
解得 故选B.
3. 解析: (1) 证明: 方法一: ∵△ABD与△ACE均为等边三角形, ∴AD=AB,AC=AE, 且 ∠BAD=∠CAE=60°,∴ ∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,∴△ABE≌△ADC(SAS).
方法二: ∵△ABD与△ACE均为等边三角形, ∴AD=AB, AC=AE, 且∠BAD=∠CAE=60°,
∴可将△ADC看作由△ABE绕着点A按顺时针方向旋转60°得到,
∴△ABE≌△ADC.
(2) 120° 90° 72°
②方法一: 依题意知, ∠BAD和∠CAE都是正n边形的内角, AB=AD, AE=AC,
∴ ∠BAD-∠DAE=∠CAE-∠DAE, 即∠BAE=∠DAC, ∴△ABE≌△ADC(SAS),
∴ ∠ABE=∠ADC. ∵ ∠ADC+∠ODA=180°,
∴ ∠ABO+∠ODA=180°, ∵∠ABO+∠ODA+∠DAB+∠BOC=360°, ∴ ∠BOC+∠DAB=180°, ∴∠BOC=180°-∠DAB=180°-
方法二: 同方法一可证△ABE≌△ADC.∴ ∠ABE=∠ADC, 如图1, 延长BA交CO于 F.
∵ ∠AFD+∠ABE+∠BOC=180°, ∠AFD+∠ADC+∠DAF=180°, ∴∠BOC=∠DAF=
方法三: 同方法一可证△ABE≌△ADC.
∴ ∠ABE=∠ADC.
∠ACD)=180°-(∠ADC+∠ABC+∠ACB+∠ACD),
∠ADC+∠ACD=180°-∠DAC,
方法四: 同方法一可证△ABE≌△ADC.∴ ∠AEB=∠ACD. 如图2, 连接CE,∵ ∠BEC=∠BOC+∠OCE, ∴∠AEB+∠AEC=∠BOC+∠ACD-∠ACE, ∴∠BOC=
同课章节目录
