九年级数学上册人教版第二十二章 二次函数 单元提高测试题(含答案)
文档属性
| 名称 | 九年级数学上册人教版第二十二章 二次函数 单元提高测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 07:46:04 | ||
图片预览




文档简介
九年级数学上册人教版第二十二章《二次函数》单元测试题
一、单选题
1.如图,抛物线顶点为,经过点,下列结论正确的是( )
A. B.
C. D.关于的方程无实数解
2.将抛物线向左平移2个单位,再向上平移2个单位后所得抛物线的表达式是( )
A. B.
C. D.
3.已知、两点的坐标分别为、,抛物线与线段只有一个交点,则的取值范围( )
A. B.
C. D.或
4.已知二次函数的自变量与函数的几组对应值如下表:
… 0 2 3 …
… 0 4 3 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当时,的值随值的增大而减小
C.若是抛物线上不同的两点,则
D.关于的一元二次方程有两个相等的实数根
5.在平面直角坐标系中,定义:已知是的函数,如果对于任意两个不相等的自变量,,当时,的取值范围是,那么将称为这个函数的“级封闭定义域”.例如:函数,当时,,所以是函数的“3级封闭定义域”.下列结论:①是函数的“1级封闭定义域”;②若是函数的“2级封闭定义域”,则;③若函数存在“3级封闭定义域”,则;④函数不存在“4级封闭定义域”.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.关于二次函数,有如下说法:
①图象的开口向上;②图象最低点到x轴的距离为k;
③图象的对称轴为直线;
④一次函数与二次函数的图象分别交于点,则关于x的方程的解为.
其中所有正确说法的序号是( )
A.①④ B.②④ C.①③ D.③④
7.如图,已知一次函数()的图象与二次函数()的图象交于,两点,当时,x的取值范围是( )
A. B.
C.或 D.
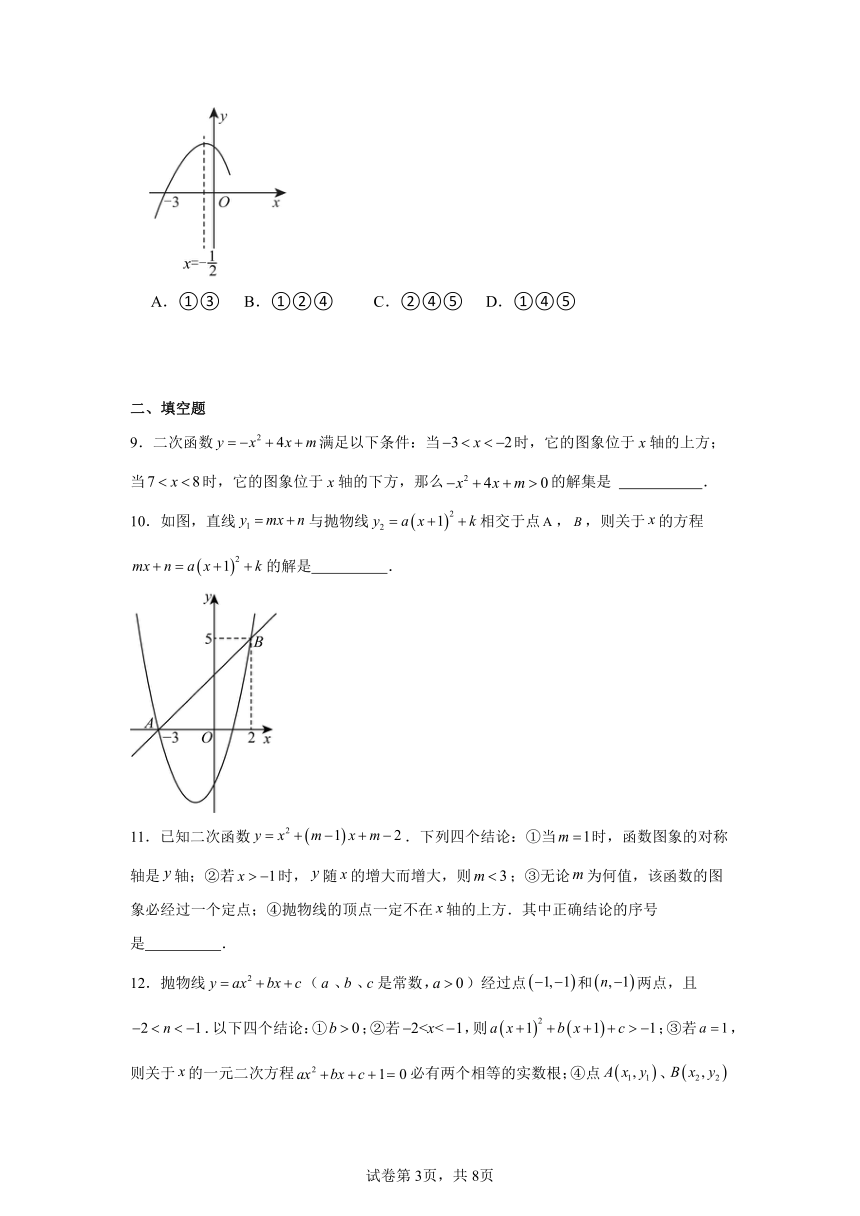
8.如图,抛物线与x轴交于点,其对称轴为直线,结合图象分析下列结论:①,②,③当时,y随x的增大而增大,④,⑤若m,n()为方程的两个根,则且.其中正确的结论有( )
A.①③ B.①②④ C.②④⑤ D.①④⑤
二、填空题
9.二次函数满足以下条件:当时,它的图象位于x轴的上方;当时,它的图象位于x轴的下方,那么的解集是 .
10.如图,直线与抛物线相交于点,,则关于的方程的解是 .
11.已知二次函数.下列四个结论:①当时,函数图象的对称轴是轴;②若时,随的增大而增大,则;③无论为何值,该函数的图象必经过一个定点;④抛物线的顶点一定不在轴的上方.其中正确结论的序号是 .
12.抛物线(是常数)经过点和两点,且.以下四个结论:①;②若,则;③若,则关于的一元二次方程必有两个相等的实数根;④点、在抛物线上,若,,总有,则.其中正确的是 (填写序号).
13.如图,已知点和,平移得到,顶点、分别与顶点对应.如果点都在抛物线上,那么点到点的距离是 .
14.如图,⊙O的半径为2,C1是函数y=2x2的图象,C2是函数y=-2x2的图象,则图中阴影部分的面积为 .
15.在平面直角坐标系中,已知抛物线.当时,该抛物线的顶点坐标是 ;若和是抛物线上的两点对于,,都有,则的取值范围是 .
16.已知抛物线的顶点为,、、、是抛物线上的四点,且线段、都垂直于抛物线的对称轴.如果,,那么的值等于 .
三、解答题
17.已知抛物线(a为常数)的顶点横坐标比抛物线的顶点横坐标小1.
(1)求a的值;
(2)设点在抛物线上,点在抛物线上.
①若,且,求n的值;
②若,求n的最大值.
18.九年级某班成立了数学学习兴趣小组,该数学兴趣小组对函数的图象和性质进行探究,过程如下,请你补充完整.
(1)①列表:如表是x,y的几组对应值,其中________,______;
x … 0 1 2 3 4 …
y … 9 0 3 0 9 …
②描点:根据表中的数值描点,请补充描出点,;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整;
(2)写出该函数的两条性质:
_________________________________________________________________________;
________________________________________________________________________;
(3)若有两个实数解,则k的取值范围是:_____________________.
19.已知二次函数,(为常数,且)图象经过点.
(1)求二次函数图象的对称轴;
(2)若,当时,的最大值为,求的值;
(3)已知,是该二次函数图象上的两点.若对于,,总有,求的取值范围.
20.如图,在平面直角坐标系中,点在直线上,已知抛物线(为常数),抛物线与轴的两个交点为点、点(其中点在点左侧),顶点为.
(1)若抛物线经过点,求抛物线的表达式;
(2)求证:的面积是一个定值,并求出这个值;
(3)已知点,抛物线的顶点恰好落在的平分线上,点在抛物线上,若四边形为梯形,求点的坐标.
21.如图,在平面直角坐标系中,抛物线 (、c是常数)的对称轴是直线 ,且经过点 ,点P 在该抛物线上,横坐标为m,设点 A 的坐标为 .
(1)求抛物线的解析式;
(2)连接、、,当的面积被x轴平分时,求m的值;
(3)将此抛物线上 P、Q两点之间的部分(包括 P、Q两点)记为图象G,过点A作x轴的平行线,交y轴于点 B,当图象G与直线只有一个公共点时,直接写出m的取值范围;
(4)以为对角线作矩形,轴,当抛物线在矩形内部y随x的增大而减小时,直接写出m的取值范围.
22.某数学兴趣小组进行项目式学习成果的展示,他们利用“杠杆原理”制作出一种投石机,如图,为检验投石机的性能,进行如下操作:将石头用投石机从处投出,石头的运动轨迹是抛物线的一部分,最终石头落在斜坡上的点C处,以水平地面为轴,为轴建立平面直角坐标系如图.已知抛物线的函数表达式为,直线的函数表达式为,米,点为抛物线的顶点,过点作轴于点,点到轴的水平距离米.
(1)请求出抛物线的函数表达式;
(2)求点的坐标.
(3)点是点左侧抛物线上一点,过点作轴交坡面于点,若石头运动到点时到坡面的铅直高度为米,求此时石头(点)到轴的距离.
23.如果直线经过抛物线的顶点,那么称直线为抛物线的准切线.如,直线经过抛物线的顶点,所以直线是抛物线的准切线.
(1)若直线为抛物线的准切线,试求的值;
(2)已知直线是抛物线()的准切线,将直线向下平移个单位,得到新直线恰好也是抛物线的准切线.
①请求出直线的解析式;
②若当时,的最小值为,试求出的值.
24.如图,二次函数的图象与x轴交于点A,B,与y轴交于点C,且图象经过点,,连接.
(1)求a,b的值.
(2)P是抛物线上的一点,且位于x轴上方,是否存在点P,使得的面积恰好为4?若存在,求出点P的坐标;若不存在,说明理由.
(3)M(不与点A,C重合)是线段上的一个动点,过点M作轴,垂足为D.延长,交抛物线于点E,过点E作,垂足为F,求周长的最大值.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十二章《二次函数》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D C C D C C C D
9./
10.
11.①③④
12.①②
13.
14.2π
15. 或
16.
17.(1)解:∵,
∴抛物线的顶点坐标为,
∵抛物线(a为常数)的顶点横坐标比抛物线的顶点横坐标小1,
∴,
解得:;
(2)①由(1)知:,
∵点在抛物线上,
∴,
∵,,
∴,
∴,
整理,得:,
∴,
∴,
∵,
∴,
∴,
∴,
∴;
②∵,,
∴,
∴,
∴,
∵,
∴,
∴当时,有最大值为:4.
18.(1)解:①当时,,即,
当时,,即,
故答案为:,;
②如图:A、B即为所描.
③补全图像如图所示.
(2)解:观察函数图形可知:
该函数关于y轴对称;
当或时,y随x的增大而减小,当或时,值y随x的增大而增大;
故答案为:该函数图象关于y轴对称;当或时,y随x的增大而减小,当或时,值y随x的增大而增大;
(3)由图象可知,当时,有3个解,
∴当时,有两个实数解,
故答案为:或.
19.(1)解:二次函数,则对称轴直线为,
由题意知,二次函数的图象过,
,则,
,
二次函数图象的对称轴是;
(2)解:二次函数图象的对称轴是,
,
,
当时,二次函数的图象草图如图1,
由图象可以看出:在范围内,点的位置最高,
∴当时,的值最大,
此时,.
解得;
(3)解:当时,函数图象草图如图2,
点在,之间的抛物线上,此时当点在点的位置时的值最小,
点关于直线的对称点为点,由于,
点在直线下方的抛物线上,
,
又,
,
解得,
又,
,
当时,函数图象的草图如图3,
点在之间的抛物线上,此时点在点处的值最小,
点关于直线的对称点为点,由于,
点在直线下方的抛物线上,
或,
又,
或,
解得或(不合题意舍去),
综上所述,的取值范围是或.
20.(1)解:将点的坐标代入一次函数表达式得:,
则,即点,
将点的坐标代入抛物线表达式得:,则,
则抛物线的表达式为:;
(2)证明:设点的横坐标分别为,
令,
则为上述方程的两个根,
则,
则点,
则,
则,
则的面积为定值;
(3)解:如图,∵恰好落在的平分线上,则,
∵点的纵坐标相同,则,
则,
则,
则,
即,
解得:( 不合题意的值已舍去),
则抛物线的表达式为:,
则点的坐标分别为:;
四边形为梯形,
当时,
设直线表达式为,
由点的坐标得,解得:,
直线表达式为,
设直线的表达式为:,代入,得:,解得:,
则直线的表达式为:,
当时,
设直线表达式为,
由点的坐标得,解得:,
直线表达式为,
设直线的表达式为:,代入,得:,解得:,
则直线的表达式为:,
分别联立和抛物线的表达式得:或,
解得:或(不合题意的值已舍去),
即点或.
21.(1)解:∵,
∴,
即,
∵抛物线 (、c是常数)的对称轴是直线 ,
∴,
∴,
∴;
(2)解:如图:
∵点P 在该抛物线上,横坐标为m,
∴,
∵的面积被x轴平分,
∴是的中线,
∵点A的坐标为.
∴,
整理得,
,
∴,
故;
(3)解:∵设点 A 的坐标为,过点A作x轴的平行线,交y轴于点 B,
∴直线的解析式为,
依题意,,
∴顶点坐标为,
则关于对称轴对称的点为,
∵将此抛物线上 P、Q两点之间的部分(包括 P、Q两点)记为图象G,且图象G与直线只有一个公共点时,
当经过点,得,
解得;
当经过点,得,
解得,
当点P在直线的下方,
则,
解得,
当经过点,得,
整理得,
解得或,
当直线在点的上方,点Q的下方(或经过点Q)时,
则;
∵,
∴,
综上:故图象G与直线只有一个公共点时,则或或或;
(4)解:∵以为对角线作矩形,轴,
∴当时,如图所示:
此时抛物线在矩形内部y随x的增大而减小,符合题意;
当时,如图所示:
此时抛物线在矩形内部y随x的增大而减小,符合题意;
当时,
则整理得,
解得或,
当时,如图所示:
此时抛物线在矩形内部y随x的增大而减小,符合题意;
当时,如图所示:
此时抛物线在矩形内部y随x的增大而增大,不符合题意;
综上:抛物线在矩形内部y随x的增大而减小时, m的取值范围为或或.
22.(1)解:由题可得,将代入,得,
∴,
∵抛物线的顶点横坐标为,
∴,
∴,
∴抛物线的函数表达式为;
(2)解:联立,
得(负值舍去),
∴;
(3)解:由题意可得,,
解得,(舍去),
∴此时石头到轴的距离为米.
23.(1)解:,
顶点为,
直线为抛物线的准切线,
,
解得,;
(2)①,
顶点为,
直线向下平移个单位,得到直线:,
直线、都是抛物线的准切线,
∴方程的解是,
即,
∵
即直线的解析式为:,
②顶点为在直线:上,
∴,
,
∴抛物线的表达式为:,
当时,,
当时,,
∵,顶点为,
i)当,即时,在,取得最小值,
∴,
解得,或(舍去),
ii)当,即时,在顶点处,取得最小值,
∴
,
iii)当,即时,在,取得最小值,
∴,
方程无解,
综上所述,或;
24.(1)∵二次函数的图象经过点,,
∴
解得
(2)存在.由(1),得,,
∴二次函数的解析式为.
令,得,
解得,.
∵二次函数的图象与x轴交于点A,B,
∴点,,
∴.
设点,
∴,
∴,
解得,,
∴点,.
(3)令,得,
∴点,
设直线AC的解析式为
解得
∴直线的解析式为.
设点,则点,
∴.
∵点,
∴.
∵,
∴.
∵轴,
∴∥轴,
∴,
∴,
∴,
∴的周长
.
∵
∴当时,的周长有最大值,最大值为,
∴的周长的最大值为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,抛物线顶点为,经过点,下列结论正确的是( )
A. B.
C. D.关于的方程无实数解
2.将抛物线向左平移2个单位,再向上平移2个单位后所得抛物线的表达式是( )
A. B.
C. D.
3.已知、两点的坐标分别为、,抛物线与线段只有一个交点,则的取值范围( )
A. B.
C. D.或
4.已知二次函数的自变量与函数的几组对应值如下表:
… 0 2 3 …
… 0 4 3 …
则下列关于这个二次函数的结论正确的是( )
A.图象的开口向上
B.当时,的值随值的增大而减小
C.若是抛物线上不同的两点,则
D.关于的一元二次方程有两个相等的实数根
5.在平面直角坐标系中,定义:已知是的函数,如果对于任意两个不相等的自变量,,当时,的取值范围是,那么将称为这个函数的“级封闭定义域”.例如:函数,当时,,所以是函数的“3级封闭定义域”.下列结论:①是函数的“1级封闭定义域”;②若是函数的“2级封闭定义域”,则;③若函数存在“3级封闭定义域”,则;④函数不存在“4级封闭定义域”.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.关于二次函数,有如下说法:
①图象的开口向上;②图象最低点到x轴的距离为k;
③图象的对称轴为直线;
④一次函数与二次函数的图象分别交于点,则关于x的方程的解为.
其中所有正确说法的序号是( )
A.①④ B.②④ C.①③ D.③④
7.如图,已知一次函数()的图象与二次函数()的图象交于,两点,当时,x的取值范围是( )
A. B.
C.或 D.
8.如图,抛物线与x轴交于点,其对称轴为直线,结合图象分析下列结论:①,②,③当时,y随x的增大而增大,④,⑤若m,n()为方程的两个根,则且.其中正确的结论有( )
A.①③ B.①②④ C.②④⑤ D.①④⑤
二、填空题
9.二次函数满足以下条件:当时,它的图象位于x轴的上方;当时,它的图象位于x轴的下方,那么的解集是 .
10.如图,直线与抛物线相交于点,,则关于的方程的解是 .
11.已知二次函数.下列四个结论:①当时,函数图象的对称轴是轴;②若时,随的增大而增大,则;③无论为何值,该函数的图象必经过一个定点;④抛物线的顶点一定不在轴的上方.其中正确结论的序号是 .
12.抛物线(是常数)经过点和两点,且.以下四个结论:①;②若,则;③若,则关于的一元二次方程必有两个相等的实数根;④点、在抛物线上,若,,总有,则.其中正确的是 (填写序号).
13.如图,已知点和,平移得到,顶点、分别与顶点对应.如果点都在抛物线上,那么点到点的距离是 .
14.如图,⊙O的半径为2,C1是函数y=2x2的图象,C2是函数y=-2x2的图象,则图中阴影部分的面积为 .
15.在平面直角坐标系中,已知抛物线.当时,该抛物线的顶点坐标是 ;若和是抛物线上的两点对于,,都有,则的取值范围是 .
16.已知抛物线的顶点为,、、、是抛物线上的四点,且线段、都垂直于抛物线的对称轴.如果,,那么的值等于 .
三、解答题
17.已知抛物线(a为常数)的顶点横坐标比抛物线的顶点横坐标小1.
(1)求a的值;
(2)设点在抛物线上,点在抛物线上.
①若,且,求n的值;
②若,求n的最大值.
18.九年级某班成立了数学学习兴趣小组,该数学兴趣小组对函数的图象和性质进行探究,过程如下,请你补充完整.
(1)①列表:如表是x,y的几组对应值,其中________,______;
x … 0 1 2 3 4 …
y … 9 0 3 0 9 …
②描点:根据表中的数值描点,请补充描出点,;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整;
(2)写出该函数的两条性质:
_________________________________________________________________________;
________________________________________________________________________;
(3)若有两个实数解,则k的取值范围是:_____________________.
19.已知二次函数,(为常数,且)图象经过点.
(1)求二次函数图象的对称轴;
(2)若,当时,的最大值为,求的值;
(3)已知,是该二次函数图象上的两点.若对于,,总有,求的取值范围.
20.如图,在平面直角坐标系中,点在直线上,已知抛物线(为常数),抛物线与轴的两个交点为点、点(其中点在点左侧),顶点为.
(1)若抛物线经过点,求抛物线的表达式;
(2)求证:的面积是一个定值,并求出这个值;
(3)已知点,抛物线的顶点恰好落在的平分线上,点在抛物线上,若四边形为梯形,求点的坐标.
21.如图,在平面直角坐标系中,抛物线 (、c是常数)的对称轴是直线 ,且经过点 ,点P 在该抛物线上,横坐标为m,设点 A 的坐标为 .
(1)求抛物线的解析式;
(2)连接、、,当的面积被x轴平分时,求m的值;
(3)将此抛物线上 P、Q两点之间的部分(包括 P、Q两点)记为图象G,过点A作x轴的平行线,交y轴于点 B,当图象G与直线只有一个公共点时,直接写出m的取值范围;
(4)以为对角线作矩形,轴,当抛物线在矩形内部y随x的增大而减小时,直接写出m的取值范围.
22.某数学兴趣小组进行项目式学习成果的展示,他们利用“杠杆原理”制作出一种投石机,如图,为检验投石机的性能,进行如下操作:将石头用投石机从处投出,石头的运动轨迹是抛物线的一部分,最终石头落在斜坡上的点C处,以水平地面为轴,为轴建立平面直角坐标系如图.已知抛物线的函数表达式为,直线的函数表达式为,米,点为抛物线的顶点,过点作轴于点,点到轴的水平距离米.
(1)请求出抛物线的函数表达式;
(2)求点的坐标.
(3)点是点左侧抛物线上一点,过点作轴交坡面于点,若石头运动到点时到坡面的铅直高度为米,求此时石头(点)到轴的距离.
23.如果直线经过抛物线的顶点,那么称直线为抛物线的准切线.如,直线经过抛物线的顶点,所以直线是抛物线的准切线.
(1)若直线为抛物线的准切线,试求的值;
(2)已知直线是抛物线()的准切线,将直线向下平移个单位,得到新直线恰好也是抛物线的准切线.
①请求出直线的解析式;
②若当时,的最小值为,试求出的值.
24.如图,二次函数的图象与x轴交于点A,B,与y轴交于点C,且图象经过点,,连接.
(1)求a,b的值.
(2)P是抛物线上的一点,且位于x轴上方,是否存在点P,使得的面积恰好为4?若存在,求出点P的坐标;若不存在,说明理由.
(3)M(不与点A,C重合)是线段上的一个动点,过点M作轴,垂足为D.延长,交抛物线于点E,过点E作,垂足为F,求周长的最大值.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十二章《二次函数》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D C C D C C C D
9./
10.
11.①③④
12.①②
13.
14.2π
15. 或
16.
17.(1)解:∵,
∴抛物线的顶点坐标为,
∵抛物线(a为常数)的顶点横坐标比抛物线的顶点横坐标小1,
∴,
解得:;
(2)①由(1)知:,
∵点在抛物线上,
∴,
∵,,
∴,
∴,
整理,得:,
∴,
∴,
∵,
∴,
∴,
∴,
∴;
②∵,,
∴,
∴,
∴,
∵,
∴,
∴当时,有最大值为:4.
18.(1)解:①当时,,即,
当时,,即,
故答案为:,;
②如图:A、B即为所描.
③补全图像如图所示.
(2)解:观察函数图形可知:
该函数关于y轴对称;
当或时,y随x的增大而减小,当或时,值y随x的增大而增大;
故答案为:该函数图象关于y轴对称;当或时,y随x的增大而减小,当或时,值y随x的增大而增大;
(3)由图象可知,当时,有3个解,
∴当时,有两个实数解,
故答案为:或.
19.(1)解:二次函数,则对称轴直线为,
由题意知,二次函数的图象过,
,则,
,
二次函数图象的对称轴是;
(2)解:二次函数图象的对称轴是,
,
,
当时,二次函数的图象草图如图1,
由图象可以看出:在范围内,点的位置最高,
∴当时,的值最大,
此时,.
解得;
(3)解:当时,函数图象草图如图2,
点在,之间的抛物线上,此时当点在点的位置时的值最小,
点关于直线的对称点为点,由于,
点在直线下方的抛物线上,
,
又,
,
解得,
又,
,
当时,函数图象的草图如图3,
点在之间的抛物线上,此时点在点处的值最小,
点关于直线的对称点为点,由于,
点在直线下方的抛物线上,
或,
又,
或,
解得或(不合题意舍去),
综上所述,的取值范围是或.
20.(1)解:将点的坐标代入一次函数表达式得:,
则,即点,
将点的坐标代入抛物线表达式得:,则,
则抛物线的表达式为:;
(2)证明:设点的横坐标分别为,
令,
则为上述方程的两个根,
则,
则点,
则,
则,
则的面积为定值;
(3)解:如图,∵恰好落在的平分线上,则,
∵点的纵坐标相同,则,
则,
则,
则,
即,
解得:( 不合题意的值已舍去),
则抛物线的表达式为:,
则点的坐标分别为:;
四边形为梯形,
当时,
设直线表达式为,
由点的坐标得,解得:,
直线表达式为,
设直线的表达式为:,代入,得:,解得:,
则直线的表达式为:,
当时,
设直线表达式为,
由点的坐标得,解得:,
直线表达式为,
设直线的表达式为:,代入,得:,解得:,
则直线的表达式为:,
分别联立和抛物线的表达式得:或,
解得:或(不合题意的值已舍去),
即点或.
21.(1)解:∵,
∴,
即,
∵抛物线 (、c是常数)的对称轴是直线 ,
∴,
∴,
∴;
(2)解:如图:
∵点P 在该抛物线上,横坐标为m,
∴,
∵的面积被x轴平分,
∴是的中线,
∵点A的坐标为.
∴,
整理得,
,
∴,
故;
(3)解:∵设点 A 的坐标为,过点A作x轴的平行线,交y轴于点 B,
∴直线的解析式为,
依题意,,
∴顶点坐标为,
则关于对称轴对称的点为,
∵将此抛物线上 P、Q两点之间的部分(包括 P、Q两点)记为图象G,且图象G与直线只有一个公共点时,
当经过点,得,
解得;
当经过点,得,
解得,
当点P在直线的下方,
则,
解得,
当经过点,得,
整理得,
解得或,
当直线在点的上方,点Q的下方(或经过点Q)时,
则;
∵,
∴,
综上:故图象G与直线只有一个公共点时,则或或或;
(4)解:∵以为对角线作矩形,轴,
∴当时,如图所示:
此时抛物线在矩形内部y随x的增大而减小,符合题意;
当时,如图所示:
此时抛物线在矩形内部y随x的增大而减小,符合题意;
当时,
则整理得,
解得或,
当时,如图所示:
此时抛物线在矩形内部y随x的增大而减小,符合题意;
当时,如图所示:
此时抛物线在矩形内部y随x的增大而增大,不符合题意;
综上:抛物线在矩形内部y随x的增大而减小时, m的取值范围为或或.
22.(1)解:由题可得,将代入,得,
∴,
∵抛物线的顶点横坐标为,
∴,
∴,
∴抛物线的函数表达式为;
(2)解:联立,
得(负值舍去),
∴;
(3)解:由题意可得,,
解得,(舍去),
∴此时石头到轴的距离为米.
23.(1)解:,
顶点为,
直线为抛物线的准切线,
,
解得,;
(2)①,
顶点为,
直线向下平移个单位,得到直线:,
直线、都是抛物线的准切线,
∴方程的解是,
即,
∵
即直线的解析式为:,
②顶点为在直线:上,
∴,
,
∴抛物线的表达式为:,
当时,,
当时,,
∵,顶点为,
i)当,即时,在,取得最小值,
∴,
解得,或(舍去),
ii)当,即时,在顶点处,取得最小值,
∴
,
iii)当,即时,在,取得最小值,
∴,
方程无解,
综上所述,或;
24.(1)∵二次函数的图象经过点,,
∴
解得
(2)存在.由(1),得,,
∴二次函数的解析式为.
令,得,
解得,.
∵二次函数的图象与x轴交于点A,B,
∴点,,
∴.
设点,
∴,
∴,
解得,,
∴点,.
(3)令,得,
∴点,
设直线AC的解析式为
解得
∴直线的解析式为.
设点,则点,
∴.
∵点,
∴.
∵,
∴.
∵轴,
∴∥轴,
∴,
∴,
∴,
∴的周长
.
∵
∴当时,的周长有最大值,最大值为,
∴的周长的最大值为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
