人教版2024-2025学年八年级数学下册《二次根式》专项训练专题03二次根式的加减(10大题型+过关训练)(原卷版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学下册《二次根式》专项训练专题03二次根式的加减(10大题型+过关训练)(原卷版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 16:40:19 | ||
图片预览




文档简介
专题 二次根式的加减
目录
【题型一 同类二次根式】 1
【题型二 分母有理化】 1
【题型三 二次根式的加减】 2
【题型四 比较二次根式的大小】 2
【题型五 二次根式的混合运算】 2
【题型六 已知字母的值对二次根式进行化简求值】 3
【题型七 已知条件式对二次根式进行化简求值】 3
【题型八 二次根式混合运算的实际应用】 4
【题型九 二次根式中的新定义类问题】 4
【题型十 二次根式中的阅读理解类问题】 5
【题型一 同类二次根式】
例题:下列各式中,与是同类二次根式的是( )
A. B. C. D.
【变式训练】
1.如果最简二次根式与是同类二次根式,那么的值是( )
A.3 B. C.1 D.0
2.若最简二次根式与是同类二次根式,则 .
【题型二 分母有理化】
例题:化简的结果是( )
A. B. C. D.
【变式训练】
1.如果,,那么、的关系是( )
A. B. C. D.
2.化简: .
【题型三 二次根式的加减】
例题:下列计算正确的是( )
A. B.
C. D.
【变式训练】
1.计算: .
2.已知实数m,n满足,则 .
【题型四 比较二次根式的大小】
例题:下列选项中的无理数位于7和8中间的是( )
A. B. C. D.
【变式训练】
1.已知,,,则,,的大小关系是( )
A. B. C. D.
2.比较大小: (填“>”或“<”或“=”).
【题型五 二次根式的混合运算】
例题:计算:结果为 .
【变式训练】
1.计算:
(1);
(2)
2.计算
(1)
(2)
(3)
(4)
【题型六 已知字母的值对二次根式进行化简求值】
例题:已知,则代数式的值为( )
A.2 B.4 C. D.
【变式训练】
1.若,.则代数式的值是( )
A. B. C. D.3
2.已知,,则 .
【题型七 已知条件式对二次根式进行化简求值】
例题:已知,,则的值为( )
A. B. C. D.
【变式训练】
1.已知,,则的值为( )
A. B. C.4 D.
2.已知,则的值为 .
【题型八 二次根式混合运算的实际应用】
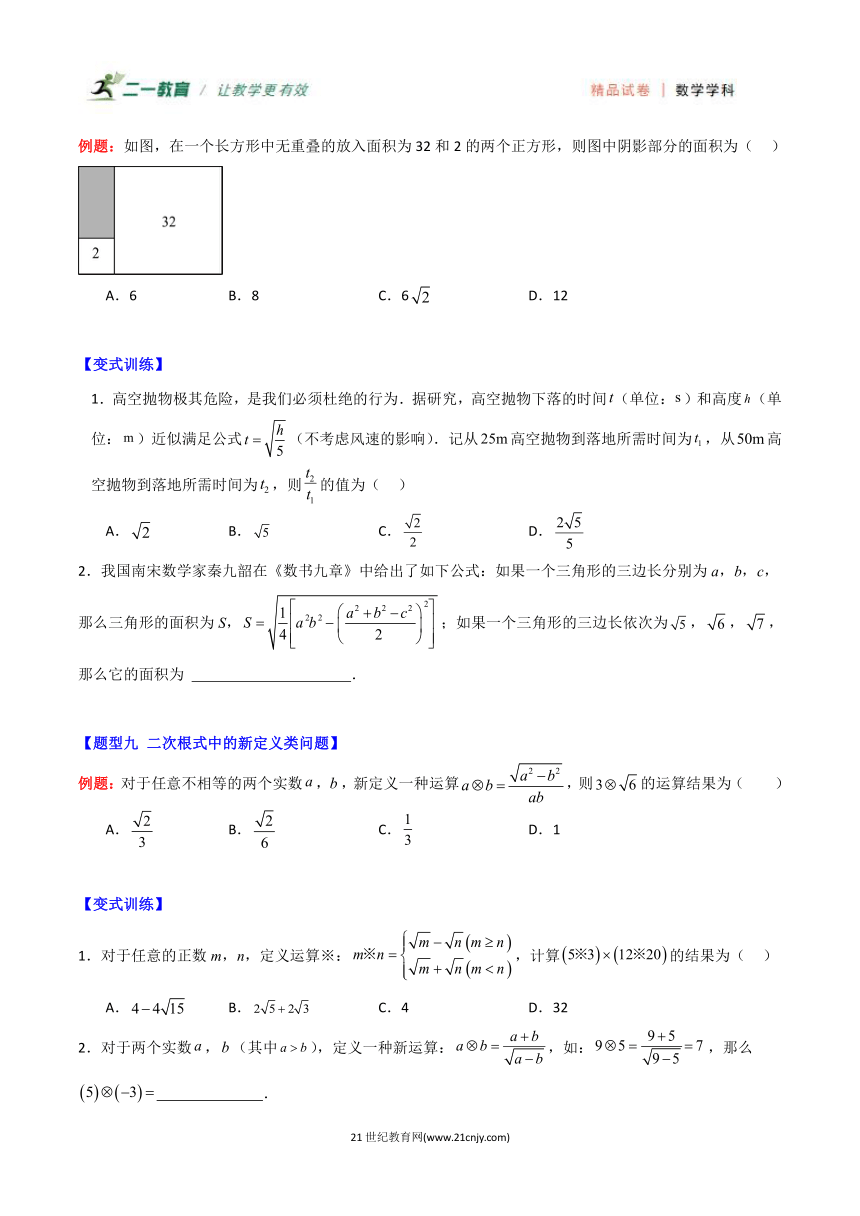
例题:如图,在一个长方形中无重叠的放入面积为32和2的两个正方形,则图中阴影部分的面积为( )
A.6 B.8 C.6 D.12
【变式训练】
1.高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间(单位:)和高度(单位:)近似满足公式(不考虑风速的影响).记从高空抛物到落地所需时间为,从高空抛物到落地所需时间为,则的值为( )
A. B. C. D.
2.我国南宋数学家秦九韶在《数书九章》中给出了如下公式:如果一个三角形的三边长分别为a,b,c,那么三角形的面积为S,;如果一个三角形的三边长依次为,,,那么它的面积为 .
【题型九 二次根式中的新定义类问题】
例题:对于任意不相等的两个实数,,新定义一种运算,则的运算结果为( )
A. B. C. D.1
【变式训练】
1.对于任意的正数m,n,定义运算※:,计算的结果为( )
A. B. C.4 D.32
2.对于两个实数,(其中),定义一种新运算:,如:,那么 .
【题型十 二次根式中的阅读理解类问题】
例题:阅读下面内容:
;
;
.
试求:
(1);
(2);
(3);(为正整数)
(4).
【变式训练】
1.阅读下面的文字,解答问题.
例如:,即,
的整数部分为2,小数部分为,
请解答:已知的整数部分是,小数部分是,且,求的值.
2.阅读下列材料,然后回答问题:
在进行类似于二次根式的运算时,通常有如下两种方法将其进一步化简:
方法一:;
方法二:.
(1)请用两种不同的方法化简:;
(2)化简:.
一、单选题
1.下列计算结果为的是( )
A. B. C. D.
2.对于任意的正数m,n定义运算“*”为:,计算的结果为( )
A. B.2 C. D.20
3.估计的值应在( )
A.和之间 B.7和8之间 C.1和2之间 D.2和3之间
4.下列计算正确的是()
A. B. C. D.
5.下列各式与是同类二次根式的是( )
A. B. C. D.
二、填空题
6.李老师在正方形中放入面积分别为27和18的正方形和正方形,重叠部分的面积为3,则剩余部分(阴影部分)的面积为 .
7.比较大小: .(填“”、“”、“”).
8.计算: .
9.分母有理化: .
10.若,那么的值为 .
三、解答题
11.高空抛物是一种不文明的危险行为,据研究,物品从离地面为h米的高处自由落下,落到地面的时间为t,经过实验,发现(不考虑阻力的影响).
(1)求物体从的高空落到地面的时间;
(2)已知从高空坠落的物体所带能量(单位:J)物体质量高度,一串质量为的钥匙经过落在地上,这串钥匙在下落过程中所带能量有多大?
(3)在(2)的结果中,你能得到什么启示?(注:杀伤无防护人体只需要的能量)
12.阅读与思考
配方思想,是初中数学重要的思想方法之一,用配方思想方法,可以简化数学运算,常用的配方公式有:,.用配方思想方法,解答下面问题:
(1)已知:,求的值;
(2)已知:,,求的值;
(3)已知:,,(,),求的值.
13.先化简,再求值:,其中.
14.计算:
(1)
(2)
15.阅读下面的材料,解决下面的问题.
;
;
;
……
(1)填空:______;
(2)猜想:当n是正整数时,______;(用含n的式子表示)
(3)计算:.
21世纪教育网(www.21cnjy.com)
专题 二次根式的加减
目录
【题型一 同类二次根式】 1
【题型二 分母有理化】 2
【题型三 二次根式的加减】 3
【题型四 比较二次根式的大小】 4
【题型五 二次根式的混合运算】 6
【题型六 已知字母的值对二次根式进行化简求值】 8
【题型七 已知条件式对二次根式进行化简求值】 9
【题型八 二次根式混合运算的实际应用】 10
【题型九 二次根式中的新定义类问题】 12
【题型十 二次根式中的阅读理解类问题】 13
【题型一 同类二次根式】
例题:下列各式中,与是同类二次根式的是( )
A. B. C. D.
【答案】B
【分析】本题考查了二次根式的化简、同类二次根式的定义,熟练掌握以上知识点是解题关键,根据同类二次根式的定义“化为最简二次根式后被开方数相同的二次根式是同类二次根式”逐项判断即可求解.
【详解】解:由题意可得,
,,,,
∴与是同类二次根式,
故选:B.
【变式训练】
1.如果最简二次根式与是同类二次根式,那么的值是( )
A.3 B. C.1 D.0
【答案】C
【分析】本题考查的是同类二次根式的概念,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.根据同类二次根式的概念列出方程,解方程求的值.
【详解】解:最简二次根式与是同类二次根式,
,
解得:,
故选:C.
2.若最简二次根式与是同类二次根式,则 .
【答案】7
【分析】本题考查了同类二次根式和最简二次根式.根据同类二次根式的定义得出,再求出答案即可.
【详解】解:∵最简二次根式与是同类二次根式,
∴,
∴.
故答案为:7.
【题型二 分母有理化】
例题:化简的结果是( )
A. B. C. D.
【答案】D
【分析】本题考查了二次根式的性质,分母有理化,二次根式的乘法,先根据二次根式的性质化简,然后分母有理化即可求解,熟练掌握运算法则是解题的关键.
【详解】解:,
故选:.
【变式训练】
1.如果,,那么、的关系是( )
A. B. C. D.
【答案】B
【分析】本题主要考查了分母有理数化,先把分母有理数化即可得出答案.
【详解】解:。
∵,
∴,
故选:B.
2.化简: .
【答案】
【分析】本题考查了二次根式的分母有理化,熟练掌握二次根式的运算法则是解题关键.分母分子同乘以,计算二次根式的乘法即可得.
【详解】解:原式
,
故答案为:.
【题型三 二次根式的加减】
例题:下列计算正确的是( )
A. B.
C. D.
【答案】A
【分析】本题考查了二次根式的加减运算,掌握二次根式加减运算法则是解题的关键.
根据合并同类二次根式的计算方法进行判定即可.
【详解】解:A、,正确,符合题意;
B、与不是同类二次根式,不能合并,故原选项错误,不符合题意;
C、,故原选项错误,不符合题意;
D、与不是同类二次根式,不能合并,故原选项错误,不符合题意;
故选:A .
【变式训练】
1.计算: .
【答案】
【分析】本题考查了二次根式的加减运算,根据二次根式的性质化简,进而根据二次根式的加减进行计算即可,掌握二次根式的性质是解题的关键.
【详解】解:,
故答案为:.
2.已知实数m,n满足,则 .
【答案】
【分析】本题考查了平方和二次根式的非负性,二次根式的化简和加减运算,根据题意求出和的值是解题的关键.根据绝对值和平方的非负性求出和的值,然后代入化简求值即可.
【详解】解:∵,
∴,
解得,
∴,
故答案为:.
【题型四 比较二次根式的大小】
例题:下列选项中的无理数位于7和8中间的是( )
A. B. C. D.
【答案】C
【分析】本题主要考查了二次根式比较大小,二次根式的化简,根据二次根式比较大小的方法可得,据此可得答案.
【详解】解:∵,
∴只有在7和8中间,
故选:C.
【变式训练】
1.已知,,,则,,的大小关系是( )
A. B. C. D.
【答案】A
【分析】此题主要考查了实数大小比较的方法,二次根式大小比较,首先分别求出的平方,并比较出它们的平方的大小关系,然后根据两个正实数,平方大的这个数也大,判断出的大小关系即可,解答此题的关键是要明确:正实数负实数,两个正实数,平方大的这个数也大.
【详解】解: ,,,
∵,
∴,
∴,
故选:A.
2.比较大小: (填“>”或“<”或“=”).
【答案】
【分析】本题考查比较实数的大小,二次根式值的大小比较,根据作差法和平方法进行比较即可.
【详解】解:,
∵,
∴,
∴,
∴;
故答案为:.
【题型五 二次根式的混合运算】
例题:计算:结果为 .
【答案】/
【分析】本题考查了二次根式的混合运算,先根据二次根式的乘除法法则和二次根式的性质化简,再算加减即可.
【详解】解:
.
故答案为:.
【变式训练】
1.计算:
(1);
(2)
【答案】(1)
(2)
【分析】本题考查的是二次根式的加减运算,二次根式的混合运算;
(1)先化简各二次根式,再合并同类二次根式即可;
(2)先计算二次根式的除法运算,乘法运算,再合并即可.
【详解】(1)解:
;
(2)解:
.
2.计算
(1)
(2)
(3)
(4)
【答案】(1)
(2)
(3)
(4)
【分析】本题考查了二次根式的混合运算和完全平方公式,先把各二次根式化简为最简二次根式,然后进行二次根式的乘除加减运算,再合并即可.掌握以上知识是解答本题的关键;
(1)先利用完全平方公式化简,在通过积的乘方和二次根式的加减运算即可求解;
(2)把分子分母中的二次根式化简为最简二次根式,即可求解;
(3)先把二次根式化简为最简二次根式,然后进行二次根式的加减运算即可求解;
(4)先把二次根式化简为最简二次根式,然后进行二次根式的乘除加减运算即可求解;
【详解】(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
【题型六 已知字母的值对二次根式进行化简求值】
例题:已知,则代数式的值为( )
A.2 B.4 C. D.
【答案】A
【分析】此题考查了二次根式的运算,熟练掌握完全平方公式,二次根式的运算法则是解题的关键.
先把化成,再把代入计算即可.
【详解】解:,
当时,原式.
故选:A.
【变式训练】
1.若,.则代数式的值是( )
A. B. C. D.3
【答案】B
【分析】本题考查了二次根式的化简求值.先根据,求出,,再用因式分解法分解,最后整体代入求值即可.
【详解】解:,,
∴,
,
∴
,
故选:B.
2.已知,,则 .
【答案】10
【分析】本题主要考查二次根式的化简求值,先根据完全平方公式将原式整理成,再代入求解即可.
【详解】解:
故答案为:10.
【题型七 已知条件式对二次根式进行化简求值】
例题:已知,,则的值为( )
A. B. C. D.
【答案】B
【分析】本题主要考查完全平方公式,二次根式的混合运算,根据完全平方公式变形,即可求解.
【详解】解:∵
∴
∴,
故选:B.
【变式训练】
1.已知,,则的值为( )
A. B. C.4 D.
【答案】D
【分析】利用已知,代入求值即可.
【详解】解:,
当,时,
,,
原式.
故选:D.
【点睛】本题考查了分式化简求值,二次根式的加减.
2.已知,则的值为 .
【答案】15
【分析】本题主要考查了分母有理化、完全平方公式等知识点,掌握分母有理化成为解题的关键.
先分母有理化可得、,则、,再运用完全平方公式可得,然后整体代入即可解答.
【详解】解:∵,,
∴,,
∴.
故答案为:15.
【题型八 二次根式混合运算的实际应用】
例题:如图,在一个长方形中无重叠的放入面积为32和2的两个正方形,则图中阴影部分的面积为( )
A.6 B.8 C.6 D.12
【答案】A
【分析】本题考查了二次根式的运算,解题关键是求出阴影部分的长和宽,准确运用二次根式乘法法则进行计算.
根据正方形面积求出阴影部分的长和宽,再求面积即可.
【详解】解:由图可知,阴影部分的长为,宽为,
∴阴影部分的面积为.
故选:A.
【变式训练】
1.高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间(单位:)和高度(单位:)近似满足公式(不考虑风速的影响).记从高空抛物到落地所需时间为,从高空抛物到落地所需时间为,则的值为( )
A. B. C. D.
【答案】A
【分析】本题考查了二次根式的应用,根据题意求出、,再计算与的比值即可得解,正确进行计算是解此题的关键.
【详解】解:由题意得:,,
∴,
故选:A.
2.我国南宋数学家秦九韶在《数书九章》中给出了如下公式:如果一个三角形的三边长分别为a,b,c,那么三角形的面积为S,;如果一个三角形的三边长依次为,,,那么它的面积为 .
【答案】
【分析】本题考查二次根式的应用,解答本题的关键是明确题意,利用题目中的面积公式解答.根据题目中的面积公式,可以将的三条边长代入公式中,从而可以解答本题.
【详解】解:∵,
三边长为:,,,不妨令,,,
∴,,,
∴,
故答案为:.
【题型九 二次根式中的新定义类问题】
例题:对于任意不相等的两个实数,,新定义一种运算,则的运算结果为( )
A. B. C. D.1
【答案】B
【分析】根据题意所给新运算的运算法则进行计算即可.
【详解】解:,
故选:B.
【点睛】本题主要考查了二次根式的混合运算,解题的关键是理解题目所给新运算,熟练掌握二次根式混合运算的运算顺序和运算法则.
【变式训练】
1.对于任意的正数m,n,定义运算※:,计算的结果为( )
A. B. C.4 D.32
【答案】C
【分析】本题考查了二次根式的混合运算,理解定义的新运算是解题的关键.根据定义的新运算列出算式,然后利用二次根式的乘法和减法法则进行计算即可解答.
【详解】解:由题意得:
,
故选:C.
2.对于两个实数,(其中),定义一种新运算:,如:,那么 .
【答案】/
【分析】本题考查了实数运算,结合已知条件列出正确的算式是解题关键.
根据题意列式后利用二次根式运算法则计算即可.
【详解】解:,
,
故答案为:.
【题型十 二次根式中的阅读理解类问题】
例题:阅读下面内容:
;
;
.
试求:
(1);
(2);
(3);(为正整数)
(4).
【答案】(1)
(2)
(3)
(4)
【分析】本题考查二次根式的混合运算和分母有理化的应用,关键是掌握二次根式的运算法则.
(1)分子分母同乘以分母的有理化因式,化简即可;
(2)分子分母乘以,化简计算即可;
(3)分子分母乘以,化简计算即可;
(4)根据(3)的运算规律化简计算即可.
【详解】(1)解:;
(2)解:;
(3)解:;
(4)解:原式
.
【变式训练】
1.阅读下面的文字,解答问题.
例如:,即,
的整数部分为2,小数部分为,
请解答:已知的整数部分是,小数部分是,且,求的值.
【答案】
【分析】本题主要考查了无理数的估算,解一元一次方程,分母有理化,先仿照题意得到,则可求出m、n的值,再代值并解方程即可得到答案.
【详解】解:∵,
∴,
∴的整数部分是,小数部分是,
∴,
∵,
∴,
∴.
2.阅读下列材料,然后回答问题:
在进行类似于二次根式的运算时,通常有如下两种方法将其进一步化简:
方法一:;
方法二:.
(1)请用两种不同的方法化简:;
(2)化简:.
【答案】(1)
(2)4
【分析】本题主要考查了二次根式的混合运算,平方差公式,分母有理化等知识点,熟练掌握题中所给的两种化简方法是解题的关键.
(1)按照题中所给的两种化简方法进行化简即可;
(2)先进行分母有理化,再进行二次根式的加减混合运算即可.
【详解】(1)解:,
;
(2)解:
一、单选题
1.下列计算结果为的是( )
A. B. C. D.
【答案】C
【分析】本题考查了二次根式的加、减、乘、除运算,根据选项化简得到的结果即可作答.
【详解】A、原式,不符合题意;
B、原式,不符合题意;
C、原式,符合题意;
D、原式,不符合题意.
故选:C.
2.对于任意的正数m,n定义运算“*”为:,计算的结果为( )
A. B.2 C. D.20
【答案】B
【分析】本题主要考查了新定义下的实数运算,二次根式的混合运算,平方差公式等知识点,根据题中的新定义正确列式计算是解题的关键.
根据新定义分别求出和,然后利用平方差公式结合二次根式的混合运算法则进行计算即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
故选:B.
3.估计的值应在( )
A.和之间 B.7和8之间 C.1和2之间 D.2和3之间
【答案】D
【分析】本题主要考查了二次根式的运算,及无理数的估算,先根据二次根式的混合运算得出结果,再估计无理数的值即可.
【详解】解:原式.
∵,
∴,
所以这个值在2和3之间.
故选:D.
4.下列计算正确的是()
A. B. C. D.
【答案】B
【分析】本题考查了二次根式的混合运算,熟练掌握二次根式的性质、二次根式的乘法法则和除法法则是解决问题的关键.根据二次根式的减法运算对A选项进行判断;根据二次根式的加法运算对B选项进行判断;根据二次根式的乘法法则对C选项进行判断;根据二次根式的性质对D选项进行判断.
【详解】解:A.,所以A选项不符合题意;
B.,所以B选项符合题意;
C.,所以C选项不符合题意;
D.,所以D选项不符合题意.
故选:B.
5.下列各式与是同类二次根式的是( )
A. B. C. D.
【答案】C
【分析】此题主要考查了同类二次根式的定义,利用同类二次根式的性质与定义分别化简二次根式进而判断得出即可.
【详解】解:,
A、,与不是同类二次根式,故此选项不符合题意;
B、,与不是同类二次根式,故此选项不符合题意;
C、,与是同类二次根式,故此选项符合题意;
D、,与不是同类二次根式,故此选项不符合题意.
故选:C.
二、填空题
6.李老师在正方形中放入面积分别为27和18的正方形和正方形,重叠部分的面积为3,则剩余部分(阴影部分)的面积为 .
【答案】/
【分析】本题考查了二次根式的混合运算的应用,结合图形求出阴影部分的长和宽是解题的关键.根据题中条件分别计算阴影部分的长和宽,再根据面积公式计算即可.
【详解】解:正方形和正方形的面积分别为27和18,
,
由题意得: 正方形和正方形重叠部分为正方形,面积为3,
则重叠部分边长为,
则正方形的边长为,
剩余部分(阴影部分)的面积等于正方形的面积减去两个小正方形的面积,再加上重叠部分的面积,
剩余部分(阴影部分)的面积为,
故答案为:.
7.比较大小: .(填“”、“”、“”).
【答案】
【分析】本题考查了比较二次根式的大小,掌握二次根式的性质是解题的关键.先把化成,再进行比较即可.
【详解】解:,
,
,
故答案为:.
8.计算: .
【答案】9
【分析】本题考查了二次根式的计算,掌握二次根式运算法则以及分母有理化是解题的关键.
先分母有理化,然后合并同类二次根式即可.
【详解】解:原式
.
故答案为:9.
9.分母有理化: .
【答案】
【分析】本题考查分母有理化,分子分母同乘计算即可.
【详解】解:
,
故答案为:.
10.若,那么的值为 .
【答案】
【分析】本题考查了二次根式的混合运算、完全平方公式,熟练掌握并灵活运用完全平方公式是解题关键.利用完全平方公式将变形为,再代入的值进行运算求值即可得.
【详解】解:,
故答案为:.
三、解答题
11.高空抛物是一种不文明的危险行为,据研究,物品从离地面为h米的高处自由落下,落到地面的时间为t,经过实验,发现(不考虑阻力的影响).
(1)求物体从的高空落到地面的时间;
(2)已知从高空坠落的物体所带能量(单位:J)物体质量高度,一串质量为的钥匙经过落在地上,这串钥匙在下落过程中所带能量有多大?
(3)在(2)的结果中,你能得到什么启示?(注:杀伤无防护人体只需要的能量)
【答案】(1)
(2)
(3)严禁高空抛物
【分析】本题考查了代数式的求值,二次根式的应用,正确理解题意是解题的关键.
(1)把代入计算即可;
(2)代入求得h,进而计算即可;
(3)由于,故会对人体造成伤害,则应该禁止高空抛物
【详解】(1)解:把代入得:,
答:物体从的高空落到地面的时间为;
(2)解:代入得:,
解得:,
则从高空坠落的物体所带能量为,
答:这串钥匙在下落过程中所带能量有;
(3)解:∵,
∴对人构成伤害,
故严禁高空抛物.
12.阅读与思考
配方思想,是初中数学重要的思想方法之一,用配方思想方法,可以简化数学运算,常用的配方公式有:,.用配方思想方法,解答下面问题:
(1)已知:,求的值;
(2)已知:,,求的值;
(3)已知:,,(,),求的值.
【答案】(1)
(2)
(3)
【分析】本题主要考查完全平方公式的变形以及二次根式的混合运算,熟练掌握公式解答本题的关键.
(1)运用完全平方公式的变形求解即可;
(2)分别求出的值,再将所要求的式子变形,最后整体代入计算即可;
(3)将变形为,最后整体代入计算即可.
【详解】(1)解:∵,
∴;
(2)解:
(3)解:∵,,
∴.
13.先化简,再求值:,其中.
【答案】,原式
【分析】本题主要考查了分式的化简求值,分母有理化,先把小括号内的式子通分化简,再把除法乘法后约分化简,最后代值计算即可得到答案.
【详解】解:
,
当时,原式.
14.计算:
(1)
(2)
【答案】(1)
(2)
【分析】本题考查了实数的混合运算,二次根式的混合运算,完全平方公式,平方差公式的应用,熟练掌握相关运算法则为解题关键.
(1)根据平方根,立方根,绝对值的性质进行计算即可;
(2)利用平方差公式,完全平方公式展开计算即可.
【详解】(1)解:
;
(2)
.
15.阅读下面的材料,解决下面的问题.
;
;
;
……
(1)填空:______;
(2)猜想:当n是正整数时,______;(用含n的式子表示)
(3)计算:.
【答案】(1)
(2)
(3)44
【分析】本题主要考查了二次根式的化简,
对于(1),先通分,得,再计算即可;
对于(2),先通分,得,再计算即可;
对于(3),根据材料可得原式
,再计算.
【详解】(1)解:原式;
故答案为:;
(2)解:原式;
故答案为:;
(3)解:原式
.
21世纪教育网(www.21cnjy.com)
目录
【题型一 同类二次根式】 1
【题型二 分母有理化】 1
【题型三 二次根式的加减】 2
【题型四 比较二次根式的大小】 2
【题型五 二次根式的混合运算】 2
【题型六 已知字母的值对二次根式进行化简求值】 3
【题型七 已知条件式对二次根式进行化简求值】 3
【题型八 二次根式混合运算的实际应用】 4
【题型九 二次根式中的新定义类问题】 4
【题型十 二次根式中的阅读理解类问题】 5
【题型一 同类二次根式】
例题:下列各式中,与是同类二次根式的是( )
A. B. C. D.
【变式训练】
1.如果最简二次根式与是同类二次根式,那么的值是( )
A.3 B. C.1 D.0
2.若最简二次根式与是同类二次根式,则 .
【题型二 分母有理化】
例题:化简的结果是( )
A. B. C. D.
【变式训练】
1.如果,,那么、的关系是( )
A. B. C. D.
2.化简: .
【题型三 二次根式的加减】
例题:下列计算正确的是( )
A. B.
C. D.
【变式训练】
1.计算: .
2.已知实数m,n满足,则 .
【题型四 比较二次根式的大小】
例题:下列选项中的无理数位于7和8中间的是( )
A. B. C. D.
【变式训练】
1.已知,,,则,,的大小关系是( )
A. B. C. D.
2.比较大小: (填“>”或“<”或“=”).
【题型五 二次根式的混合运算】
例题:计算:结果为 .
【变式训练】
1.计算:
(1);
(2)
2.计算
(1)
(2)
(3)
(4)
【题型六 已知字母的值对二次根式进行化简求值】
例题:已知,则代数式的值为( )
A.2 B.4 C. D.
【变式训练】
1.若,.则代数式的值是( )
A. B. C. D.3
2.已知,,则 .
【题型七 已知条件式对二次根式进行化简求值】
例题:已知,,则的值为( )
A. B. C. D.
【变式训练】
1.已知,,则的值为( )
A. B. C.4 D.
2.已知,则的值为 .
【题型八 二次根式混合运算的实际应用】
例题:如图,在一个长方形中无重叠的放入面积为32和2的两个正方形,则图中阴影部分的面积为( )
A.6 B.8 C.6 D.12
【变式训练】
1.高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间(单位:)和高度(单位:)近似满足公式(不考虑风速的影响).记从高空抛物到落地所需时间为,从高空抛物到落地所需时间为,则的值为( )
A. B. C. D.
2.我国南宋数学家秦九韶在《数书九章》中给出了如下公式:如果一个三角形的三边长分别为a,b,c,那么三角形的面积为S,;如果一个三角形的三边长依次为,,,那么它的面积为 .
【题型九 二次根式中的新定义类问题】
例题:对于任意不相等的两个实数,,新定义一种运算,则的运算结果为( )
A. B. C. D.1
【变式训练】
1.对于任意的正数m,n,定义运算※:,计算的结果为( )
A. B. C.4 D.32
2.对于两个实数,(其中),定义一种新运算:,如:,那么 .
【题型十 二次根式中的阅读理解类问题】
例题:阅读下面内容:
;
;
.
试求:
(1);
(2);
(3);(为正整数)
(4).
【变式训练】
1.阅读下面的文字,解答问题.
例如:,即,
的整数部分为2,小数部分为,
请解答:已知的整数部分是,小数部分是,且,求的值.
2.阅读下列材料,然后回答问题:
在进行类似于二次根式的运算时,通常有如下两种方法将其进一步化简:
方法一:;
方法二:.
(1)请用两种不同的方法化简:;
(2)化简:.
一、单选题
1.下列计算结果为的是( )
A. B. C. D.
2.对于任意的正数m,n定义运算“*”为:,计算的结果为( )
A. B.2 C. D.20
3.估计的值应在( )
A.和之间 B.7和8之间 C.1和2之间 D.2和3之间
4.下列计算正确的是()
A. B. C. D.
5.下列各式与是同类二次根式的是( )
A. B. C. D.
二、填空题
6.李老师在正方形中放入面积分别为27和18的正方形和正方形,重叠部分的面积为3,则剩余部分(阴影部分)的面积为 .
7.比较大小: .(填“”、“”、“”).
8.计算: .
9.分母有理化: .
10.若,那么的值为 .
三、解答题
11.高空抛物是一种不文明的危险行为,据研究,物品从离地面为h米的高处自由落下,落到地面的时间为t,经过实验,发现(不考虑阻力的影响).
(1)求物体从的高空落到地面的时间;
(2)已知从高空坠落的物体所带能量(单位:J)物体质量高度,一串质量为的钥匙经过落在地上,这串钥匙在下落过程中所带能量有多大?
(3)在(2)的结果中,你能得到什么启示?(注:杀伤无防护人体只需要的能量)
12.阅读与思考
配方思想,是初中数学重要的思想方法之一,用配方思想方法,可以简化数学运算,常用的配方公式有:,.用配方思想方法,解答下面问题:
(1)已知:,求的值;
(2)已知:,,求的值;
(3)已知:,,(,),求的值.
13.先化简,再求值:,其中.
14.计算:
(1)
(2)
15.阅读下面的材料,解决下面的问题.
;
;
;
……
(1)填空:______;
(2)猜想:当n是正整数时,______;(用含n的式子表示)
(3)计算:.
21世纪教育网(www.21cnjy.com)
专题 二次根式的加减
目录
【题型一 同类二次根式】 1
【题型二 分母有理化】 2
【题型三 二次根式的加减】 3
【题型四 比较二次根式的大小】 4
【题型五 二次根式的混合运算】 6
【题型六 已知字母的值对二次根式进行化简求值】 8
【题型七 已知条件式对二次根式进行化简求值】 9
【题型八 二次根式混合运算的实际应用】 10
【题型九 二次根式中的新定义类问题】 12
【题型十 二次根式中的阅读理解类问题】 13
【题型一 同类二次根式】
例题:下列各式中,与是同类二次根式的是( )
A. B. C. D.
【答案】B
【分析】本题考查了二次根式的化简、同类二次根式的定义,熟练掌握以上知识点是解题关键,根据同类二次根式的定义“化为最简二次根式后被开方数相同的二次根式是同类二次根式”逐项判断即可求解.
【详解】解:由题意可得,
,,,,
∴与是同类二次根式,
故选:B.
【变式训练】
1.如果最简二次根式与是同类二次根式,那么的值是( )
A.3 B. C.1 D.0
【答案】C
【分析】本题考查的是同类二次根式的概念,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.根据同类二次根式的概念列出方程,解方程求的值.
【详解】解:最简二次根式与是同类二次根式,
,
解得:,
故选:C.
2.若最简二次根式与是同类二次根式,则 .
【答案】7
【分析】本题考查了同类二次根式和最简二次根式.根据同类二次根式的定义得出,再求出答案即可.
【详解】解:∵最简二次根式与是同类二次根式,
∴,
∴.
故答案为:7.
【题型二 分母有理化】
例题:化简的结果是( )
A. B. C. D.
【答案】D
【分析】本题考查了二次根式的性质,分母有理化,二次根式的乘法,先根据二次根式的性质化简,然后分母有理化即可求解,熟练掌握运算法则是解题的关键.
【详解】解:,
故选:.
【变式训练】
1.如果,,那么、的关系是( )
A. B. C. D.
【答案】B
【分析】本题主要考查了分母有理数化,先把分母有理数化即可得出答案.
【详解】解:。
∵,
∴,
故选:B.
2.化简: .
【答案】
【分析】本题考查了二次根式的分母有理化,熟练掌握二次根式的运算法则是解题关键.分母分子同乘以,计算二次根式的乘法即可得.
【详解】解:原式
,
故答案为:.
【题型三 二次根式的加减】
例题:下列计算正确的是( )
A. B.
C. D.
【答案】A
【分析】本题考查了二次根式的加减运算,掌握二次根式加减运算法则是解题的关键.
根据合并同类二次根式的计算方法进行判定即可.
【详解】解:A、,正确,符合题意;
B、与不是同类二次根式,不能合并,故原选项错误,不符合题意;
C、,故原选项错误,不符合题意;
D、与不是同类二次根式,不能合并,故原选项错误,不符合题意;
故选:A .
【变式训练】
1.计算: .
【答案】
【分析】本题考查了二次根式的加减运算,根据二次根式的性质化简,进而根据二次根式的加减进行计算即可,掌握二次根式的性质是解题的关键.
【详解】解:,
故答案为:.
2.已知实数m,n满足,则 .
【答案】
【分析】本题考查了平方和二次根式的非负性,二次根式的化简和加减运算,根据题意求出和的值是解题的关键.根据绝对值和平方的非负性求出和的值,然后代入化简求值即可.
【详解】解:∵,
∴,
解得,
∴,
故答案为:.
【题型四 比较二次根式的大小】
例题:下列选项中的无理数位于7和8中间的是( )
A. B. C. D.
【答案】C
【分析】本题主要考查了二次根式比较大小,二次根式的化简,根据二次根式比较大小的方法可得,据此可得答案.
【详解】解:∵,
∴只有在7和8中间,
故选:C.
【变式训练】
1.已知,,,则,,的大小关系是( )
A. B. C. D.
【答案】A
【分析】此题主要考查了实数大小比较的方法,二次根式大小比较,首先分别求出的平方,并比较出它们的平方的大小关系,然后根据两个正实数,平方大的这个数也大,判断出的大小关系即可,解答此题的关键是要明确:正实数负实数,两个正实数,平方大的这个数也大.
【详解】解: ,,,
∵,
∴,
∴,
故选:A.
2.比较大小: (填“>”或“<”或“=”).
【答案】
【分析】本题考查比较实数的大小,二次根式值的大小比较,根据作差法和平方法进行比较即可.
【详解】解:,
∵,
∴,
∴,
∴;
故答案为:.
【题型五 二次根式的混合运算】
例题:计算:结果为 .
【答案】/
【分析】本题考查了二次根式的混合运算,先根据二次根式的乘除法法则和二次根式的性质化简,再算加减即可.
【详解】解:
.
故答案为:.
【变式训练】
1.计算:
(1);
(2)
【答案】(1)
(2)
【分析】本题考查的是二次根式的加减运算,二次根式的混合运算;
(1)先化简各二次根式,再合并同类二次根式即可;
(2)先计算二次根式的除法运算,乘法运算,再合并即可.
【详解】(1)解:
;
(2)解:
.
2.计算
(1)
(2)
(3)
(4)
【答案】(1)
(2)
(3)
(4)
【分析】本题考查了二次根式的混合运算和完全平方公式,先把各二次根式化简为最简二次根式,然后进行二次根式的乘除加减运算,再合并即可.掌握以上知识是解答本题的关键;
(1)先利用完全平方公式化简,在通过积的乘方和二次根式的加减运算即可求解;
(2)把分子分母中的二次根式化简为最简二次根式,即可求解;
(3)先把二次根式化简为最简二次根式,然后进行二次根式的加减运算即可求解;
(4)先把二次根式化简为最简二次根式,然后进行二次根式的乘除加减运算即可求解;
【详解】(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
【题型六 已知字母的值对二次根式进行化简求值】
例题:已知,则代数式的值为( )
A.2 B.4 C. D.
【答案】A
【分析】此题考查了二次根式的运算,熟练掌握完全平方公式,二次根式的运算法则是解题的关键.
先把化成,再把代入计算即可.
【详解】解:,
当时,原式.
故选:A.
【变式训练】
1.若,.则代数式的值是( )
A. B. C. D.3
【答案】B
【分析】本题考查了二次根式的化简求值.先根据,求出,,再用因式分解法分解,最后整体代入求值即可.
【详解】解:,,
∴,
,
∴
,
故选:B.
2.已知,,则 .
【答案】10
【分析】本题主要考查二次根式的化简求值,先根据完全平方公式将原式整理成,再代入求解即可.
【详解】解:
故答案为:10.
【题型七 已知条件式对二次根式进行化简求值】
例题:已知,,则的值为( )
A. B. C. D.
【答案】B
【分析】本题主要考查完全平方公式,二次根式的混合运算,根据完全平方公式变形,即可求解.
【详解】解:∵
∴
∴,
故选:B.
【变式训练】
1.已知,,则的值为( )
A. B. C.4 D.
【答案】D
【分析】利用已知,代入求值即可.
【详解】解:,
当,时,
,,
原式.
故选:D.
【点睛】本题考查了分式化简求值,二次根式的加减.
2.已知,则的值为 .
【答案】15
【分析】本题主要考查了分母有理化、完全平方公式等知识点,掌握分母有理化成为解题的关键.
先分母有理化可得、,则、,再运用完全平方公式可得,然后整体代入即可解答.
【详解】解:∵,,
∴,,
∴.
故答案为:15.
【题型八 二次根式混合运算的实际应用】
例题:如图,在一个长方形中无重叠的放入面积为32和2的两个正方形,则图中阴影部分的面积为( )
A.6 B.8 C.6 D.12
【答案】A
【分析】本题考查了二次根式的运算,解题关键是求出阴影部分的长和宽,准确运用二次根式乘法法则进行计算.
根据正方形面积求出阴影部分的长和宽,再求面积即可.
【详解】解:由图可知,阴影部分的长为,宽为,
∴阴影部分的面积为.
故选:A.
【变式训练】
1.高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间(单位:)和高度(单位:)近似满足公式(不考虑风速的影响).记从高空抛物到落地所需时间为,从高空抛物到落地所需时间为,则的值为( )
A. B. C. D.
【答案】A
【分析】本题考查了二次根式的应用,根据题意求出、,再计算与的比值即可得解,正确进行计算是解此题的关键.
【详解】解:由题意得:,,
∴,
故选:A.
2.我国南宋数学家秦九韶在《数书九章》中给出了如下公式:如果一个三角形的三边长分别为a,b,c,那么三角形的面积为S,;如果一个三角形的三边长依次为,,,那么它的面积为 .
【答案】
【分析】本题考查二次根式的应用,解答本题的关键是明确题意,利用题目中的面积公式解答.根据题目中的面积公式,可以将的三条边长代入公式中,从而可以解答本题.
【详解】解:∵,
三边长为:,,,不妨令,,,
∴,,,
∴,
故答案为:.
【题型九 二次根式中的新定义类问题】
例题:对于任意不相等的两个实数,,新定义一种运算,则的运算结果为( )
A. B. C. D.1
【答案】B
【分析】根据题意所给新运算的运算法则进行计算即可.
【详解】解:,
故选:B.
【点睛】本题主要考查了二次根式的混合运算,解题的关键是理解题目所给新运算,熟练掌握二次根式混合运算的运算顺序和运算法则.
【变式训练】
1.对于任意的正数m,n,定义运算※:,计算的结果为( )
A. B. C.4 D.32
【答案】C
【分析】本题考查了二次根式的混合运算,理解定义的新运算是解题的关键.根据定义的新运算列出算式,然后利用二次根式的乘法和减法法则进行计算即可解答.
【详解】解:由题意得:
,
故选:C.
2.对于两个实数,(其中),定义一种新运算:,如:,那么 .
【答案】/
【分析】本题考查了实数运算,结合已知条件列出正确的算式是解题关键.
根据题意列式后利用二次根式运算法则计算即可.
【详解】解:,
,
故答案为:.
【题型十 二次根式中的阅读理解类问题】
例题:阅读下面内容:
;
;
.
试求:
(1);
(2);
(3);(为正整数)
(4).
【答案】(1)
(2)
(3)
(4)
【分析】本题考查二次根式的混合运算和分母有理化的应用,关键是掌握二次根式的运算法则.
(1)分子分母同乘以分母的有理化因式,化简即可;
(2)分子分母乘以,化简计算即可;
(3)分子分母乘以,化简计算即可;
(4)根据(3)的运算规律化简计算即可.
【详解】(1)解:;
(2)解:;
(3)解:;
(4)解:原式
.
【变式训练】
1.阅读下面的文字,解答问题.
例如:,即,
的整数部分为2,小数部分为,
请解答:已知的整数部分是,小数部分是,且,求的值.
【答案】
【分析】本题主要考查了无理数的估算,解一元一次方程,分母有理化,先仿照题意得到,则可求出m、n的值,再代值并解方程即可得到答案.
【详解】解:∵,
∴,
∴的整数部分是,小数部分是,
∴,
∵,
∴,
∴.
2.阅读下列材料,然后回答问题:
在进行类似于二次根式的运算时,通常有如下两种方法将其进一步化简:
方法一:;
方法二:.
(1)请用两种不同的方法化简:;
(2)化简:.
【答案】(1)
(2)4
【分析】本题主要考查了二次根式的混合运算,平方差公式,分母有理化等知识点,熟练掌握题中所给的两种化简方法是解题的关键.
(1)按照题中所给的两种化简方法进行化简即可;
(2)先进行分母有理化,再进行二次根式的加减混合运算即可.
【详解】(1)解:,
;
(2)解:
一、单选题
1.下列计算结果为的是( )
A. B. C. D.
【答案】C
【分析】本题考查了二次根式的加、减、乘、除运算,根据选项化简得到的结果即可作答.
【详解】A、原式,不符合题意;
B、原式,不符合题意;
C、原式,符合题意;
D、原式,不符合题意.
故选:C.
2.对于任意的正数m,n定义运算“*”为:,计算的结果为( )
A. B.2 C. D.20
【答案】B
【分析】本题主要考查了新定义下的实数运算,二次根式的混合运算,平方差公式等知识点,根据题中的新定义正确列式计算是解题的关键.
根据新定义分别求出和,然后利用平方差公式结合二次根式的混合运算法则进行计算即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
故选:B.
3.估计的值应在( )
A.和之间 B.7和8之间 C.1和2之间 D.2和3之间
【答案】D
【分析】本题主要考查了二次根式的运算,及无理数的估算,先根据二次根式的混合运算得出结果,再估计无理数的值即可.
【详解】解:原式.
∵,
∴,
所以这个值在2和3之间.
故选:D.
4.下列计算正确的是()
A. B. C. D.
【答案】B
【分析】本题考查了二次根式的混合运算,熟练掌握二次根式的性质、二次根式的乘法法则和除法法则是解决问题的关键.根据二次根式的减法运算对A选项进行判断;根据二次根式的加法运算对B选项进行判断;根据二次根式的乘法法则对C选项进行判断;根据二次根式的性质对D选项进行判断.
【详解】解:A.,所以A选项不符合题意;
B.,所以B选项符合题意;
C.,所以C选项不符合题意;
D.,所以D选项不符合题意.
故选:B.
5.下列各式与是同类二次根式的是( )
A. B. C. D.
【答案】C
【分析】此题主要考查了同类二次根式的定义,利用同类二次根式的性质与定义分别化简二次根式进而判断得出即可.
【详解】解:,
A、,与不是同类二次根式,故此选项不符合题意;
B、,与不是同类二次根式,故此选项不符合题意;
C、,与是同类二次根式,故此选项符合题意;
D、,与不是同类二次根式,故此选项不符合题意.
故选:C.
二、填空题
6.李老师在正方形中放入面积分别为27和18的正方形和正方形,重叠部分的面积为3,则剩余部分(阴影部分)的面积为 .
【答案】/
【分析】本题考查了二次根式的混合运算的应用,结合图形求出阴影部分的长和宽是解题的关键.根据题中条件分别计算阴影部分的长和宽,再根据面积公式计算即可.
【详解】解:正方形和正方形的面积分别为27和18,
,
由题意得: 正方形和正方形重叠部分为正方形,面积为3,
则重叠部分边长为,
则正方形的边长为,
剩余部分(阴影部分)的面积等于正方形的面积减去两个小正方形的面积,再加上重叠部分的面积,
剩余部分(阴影部分)的面积为,
故答案为:.
7.比较大小: .(填“”、“”、“”).
【答案】
【分析】本题考查了比较二次根式的大小,掌握二次根式的性质是解题的关键.先把化成,再进行比较即可.
【详解】解:,
,
,
故答案为:.
8.计算: .
【答案】9
【分析】本题考查了二次根式的计算,掌握二次根式运算法则以及分母有理化是解题的关键.
先分母有理化,然后合并同类二次根式即可.
【详解】解:原式
.
故答案为:9.
9.分母有理化: .
【答案】
【分析】本题考查分母有理化,分子分母同乘计算即可.
【详解】解:
,
故答案为:.
10.若,那么的值为 .
【答案】
【分析】本题考查了二次根式的混合运算、完全平方公式,熟练掌握并灵活运用完全平方公式是解题关键.利用完全平方公式将变形为,再代入的值进行运算求值即可得.
【详解】解:,
故答案为:.
三、解答题
11.高空抛物是一种不文明的危险行为,据研究,物品从离地面为h米的高处自由落下,落到地面的时间为t,经过实验,发现(不考虑阻力的影响).
(1)求物体从的高空落到地面的时间;
(2)已知从高空坠落的物体所带能量(单位:J)物体质量高度,一串质量为的钥匙经过落在地上,这串钥匙在下落过程中所带能量有多大?
(3)在(2)的结果中,你能得到什么启示?(注:杀伤无防护人体只需要的能量)
【答案】(1)
(2)
(3)严禁高空抛物
【分析】本题考查了代数式的求值,二次根式的应用,正确理解题意是解题的关键.
(1)把代入计算即可;
(2)代入求得h,进而计算即可;
(3)由于,故会对人体造成伤害,则应该禁止高空抛物
【详解】(1)解:把代入得:,
答:物体从的高空落到地面的时间为;
(2)解:代入得:,
解得:,
则从高空坠落的物体所带能量为,
答:这串钥匙在下落过程中所带能量有;
(3)解:∵,
∴对人构成伤害,
故严禁高空抛物.
12.阅读与思考
配方思想,是初中数学重要的思想方法之一,用配方思想方法,可以简化数学运算,常用的配方公式有:,.用配方思想方法,解答下面问题:
(1)已知:,求的值;
(2)已知:,,求的值;
(3)已知:,,(,),求的值.
【答案】(1)
(2)
(3)
【分析】本题主要考查完全平方公式的变形以及二次根式的混合运算,熟练掌握公式解答本题的关键.
(1)运用完全平方公式的变形求解即可;
(2)分别求出的值,再将所要求的式子变形,最后整体代入计算即可;
(3)将变形为,最后整体代入计算即可.
【详解】(1)解:∵,
∴;
(2)解:
(3)解:∵,,
∴.
13.先化简,再求值:,其中.
【答案】,原式
【分析】本题主要考查了分式的化简求值,分母有理化,先把小括号内的式子通分化简,再把除法乘法后约分化简,最后代值计算即可得到答案.
【详解】解:
,
当时,原式.
14.计算:
(1)
(2)
【答案】(1)
(2)
【分析】本题考查了实数的混合运算,二次根式的混合运算,完全平方公式,平方差公式的应用,熟练掌握相关运算法则为解题关键.
(1)根据平方根,立方根,绝对值的性质进行计算即可;
(2)利用平方差公式,完全平方公式展开计算即可.
【详解】(1)解:
;
(2)
.
15.阅读下面的材料,解决下面的问题.
;
;
;
……
(1)填空:______;
(2)猜想:当n是正整数时,______;(用含n的式子表示)
(3)计算:.
【答案】(1)
(2)
(3)44
【分析】本题主要考查了二次根式的化简,
对于(1),先通分,得,再计算即可;
对于(2),先通分,得,再计算即可;
对于(3),根据材料可得原式
,再计算.
【详解】(1)解:原式;
故答案为:;
(2)解:原式;
故答案为:;
(3)解:原式
.
21世纪教育网(www.21cnjy.com)
