江苏省镇江市2024-2025学年七年级(下)期中数学试卷(PDF版,含答案)
文档属性
| 名称 | 江苏省镇江市2024-2025学年七年级(下)期中数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 22:47:09 | ||
图片预览



文档简介
2024-2025学年江苏省镇江市七年级(下)期中数学试卷
一、选择题:本题共 10小题,每小题 3分,共 30分。在每小题给出的选项中,只有一项是符合题目要求
的。
1.剪纸是中国独特的民间艺术,如图是我国传统文化中的“福禄寿喜”剪纸图,其中是中心对称图形的是
( )
A. B. C. D.
2.下列运算,结果正确的是( )
A. 3 2 = B. ( + )2 = 2 + 2
C. (3 3)2 = 9 6 D. ( 4)3 = 7
3 1.在方程2 = + 1,2 + 3 = 5,2 1 = , + = 0 中二元一次方程的个数为( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
4.下列四组数值是二元一次方程 2 + = 10 的解是( )
A. = 1 = 4 = 2 = 2 = 5 B. = 2 C. = 4 D. = 3
5.已知 = 8, = 16,则 的值为( )
A. 12 B. 6 C. 8 D. 2
6.已知 + = 5, = 3,则( + 1)( + 1) =( )
A. 3 B. 2 C. 3 D. 9
7.如( + )与( + 4)的乘积中不含 的一次项,则 的值为( )
A. 4 B. 4 C. 0 D. 1
8 1.计算( )20242 × 2
2025 × 3 的值等于( )
A. 3 B. 3 C. 6 D. 6
9.小芳和小明在手工课上各自制作楼梯模型(中间是空的),如下图,则他们所用的材料( )
A.一样长 B.小明的长 C.小芳的长 D.不能确定
第 1页,共 10页
10.如图,格点三角形甲逆时针旋转 90°后得到格点三角形乙,则其旋转中心是( )
A.点 B.点 C.点 D.点
二、填空题:本题共 6小题,每小题 3分,共 18分。
11.某微生物细胞直径为 0.000035 米,将 0.000035 用科学记数法表示为______.
12 = 2.已知 = 1是方程 + = 3 的解,则代数式 2 + 3 的值为______.
13.若 2 + 4 = 0,则22 × 2 = ______.
14.如图,等腰△ 中, = , = 14 ,点 是 的中点, = 5 ,将
线段 沿 方向平移 7 得到线段 ,点 、 分别落在边 、 上,则△
的周长是______ .
15.如图,在直角△ 中,∠ = 90°,分别以两直角边为腰作等腰直角三角形,
记 1 = △ , 2 = △ ,其中 1 + 2 = 9, = 6,则图中阴影部分面积为______.
16.有许多非常复杂的几何图形可以由简单的数学规则创造出来.比如谢尔宾斯基三角形,它的构造方法是:
以一个等边三角形为初始图形,每次将等边三角形分割成 4 个边长为原来一半的小三角形,并去掉其中间
的小三角形,将这个过程反复进行下去,就可以得到无限细节的谢尔宾斯基三角形,如图所示,按此规律,
第 个图形中剩余的三角形(黑色三角形)的个数为______.
三、解答题:本题共 8小题,共 72分。解答应写出文字说明,证明过程或演算步骤。
第 2页,共 10页
17.(本小题 8 分)
计算:
(1)( 1)2024 + (2025 )0 ( 1 ) 12 ;
(2)2024 × 2026 20252.
18.(本小题 10 分)
计算:
(1)8 5 ( )3 + ( 3 4)2;
(2)( )( + 3 ) ( + )2.
19.(本小题 10 分)
解二元一次方程组:
= 3
(1) 3 8 = 4;
3 + 2 = 12
(2) 5 6 = 8.
20.(本小题 8 分)
如图,在正方形网格中,每个小正方形的边长都是 1 个单位长度,△ 的三个顶点都在格点上.
(1)平移图中的△ ,使点 移到点 1的位置,画出平移后的△ 1 1 1;画出△ 关于点 成中心对称的
△ 2 2 2;
(2) △ 1 1 1与△ 2 2 2是否成中心对称?若是,画出其对称中心点 的位置;
(3)在直线 上找一点 ,使△ 的周长最小,请在图中标出点 的位置.
21.(本小题 8 分)
如图,是相同的小正方形拼成的正方形网格,其中的两个小正方形已涂色,请你在图中再涂两个小正方形,
并满足:①4 个涂色的小正方形中,每个小正方形至少与其余 3 个小正方形中的 1 个有公共点;②连同空
第 3页,共 10页
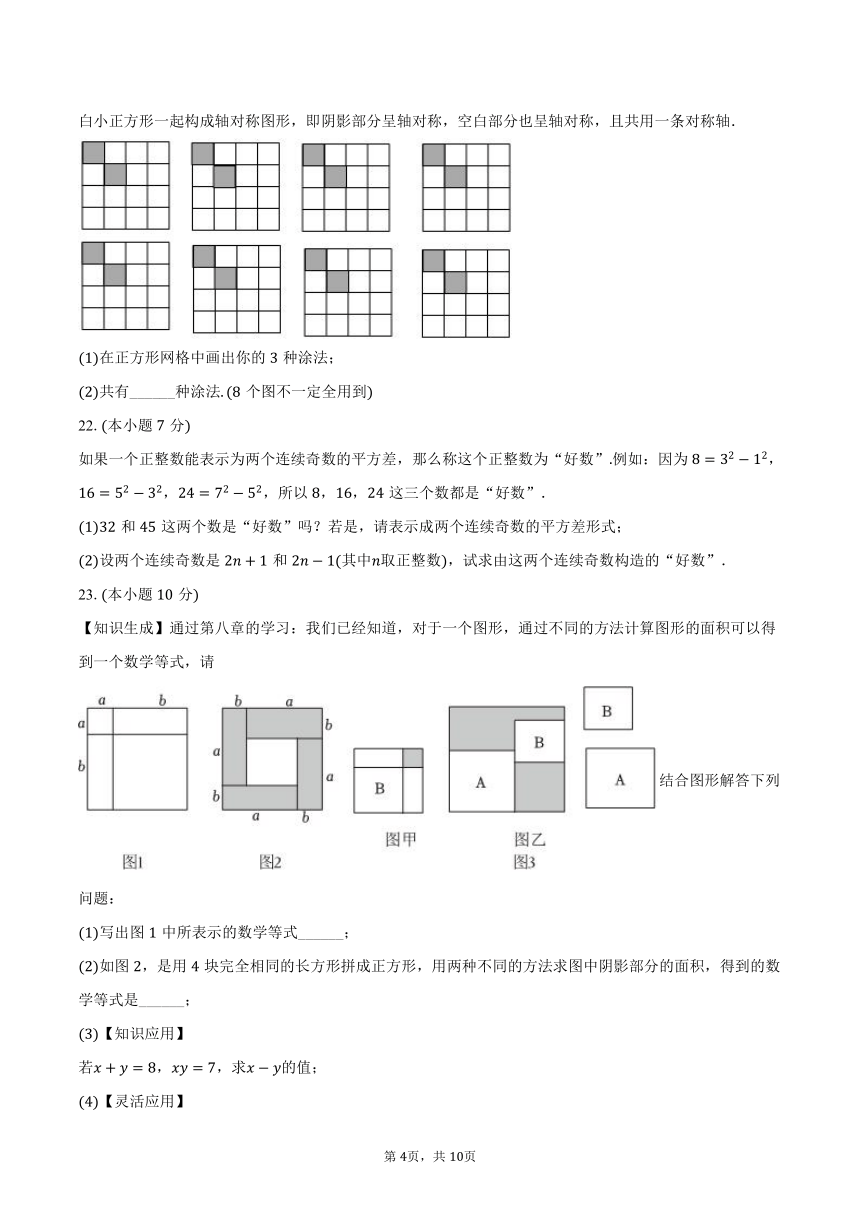
白小正方形一起构成轴对称图形,即阴影部分呈轴对称,空白部分也呈轴对称,且共用一条对称轴.
(1)在正方形网格中画出你的 3 种涂法;
(2)共有______种涂法. (8 个图不一定全用到)
22.(本小题 7 分)
如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“好数”.例如:因为 8 = 32 12,
16 = 52 32,24 = 72 52,所以 8,16,24 这三个数都是“好数”.
(1)32 和 45 这两个数是“好数”吗?若是,请表示成两个连续奇数的平方差形式;
(2)设两个连续奇数是 2 + 1 和 2 1(其中 取正整数),试求由这两个连续奇数构造的“好数”.
23.(本小题 10 分)
【知识生成】通过第八章的学习:我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得
到一个数学等式,请
结合图形解答下列
问题:
(1)写出图 1 中所表示的数学等式______;
(2)如图 2,是用 4 块完全相同的长方形拼成正方形,用两种不同的方法求图中阴影部分的面积,得到的数
学等式是______;
(3)【知识应用】
若 + = 8, = 7,求 的值;
(4)【灵活应用】
第 4页,共 10页
图 3 中有两个正方形 、 ,现将 放在 的内部得到图甲,将 、 并列放置后构造新的正方形得到图乙.若
图甲和图乙中阴影部分的面积分别为 3 和 12,则正方形 , 的面积之和是______.
24.(本小题 11 分)
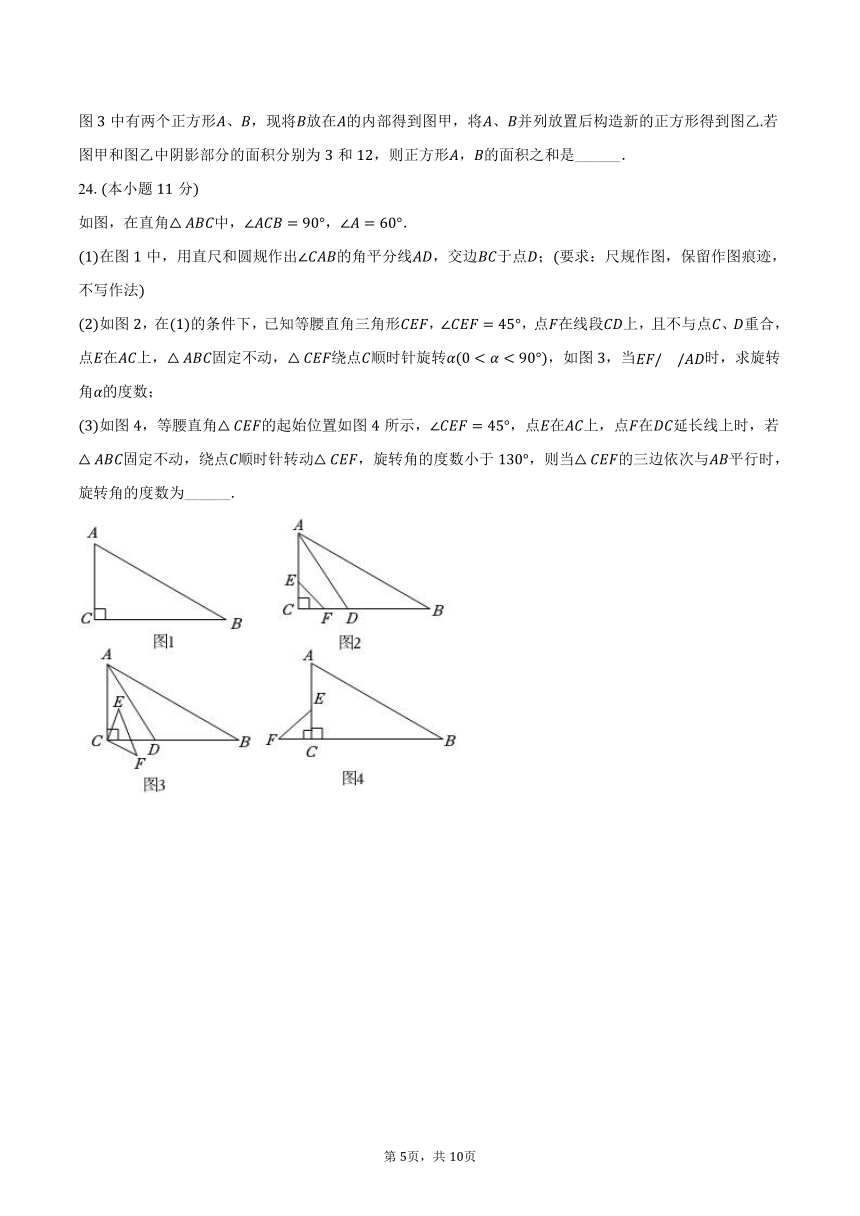
如图,在直角△ 中,∠ = 90°,∠ = 60°.
(1)在图 1 中,用直尺和圆规作出∠ 的角平分线 ,交边 于点 ;(要求:尺规作图,保留作图痕迹,
不写作法)
(2)如图 2,在(1)的条件下,已知等腰直角三角形 ,∠ = 45°,点 在线段 上,且不与点 、 重合,
点 在 上,△ 固定不动,△ 绕点 顺时针旋转 (0 < < 90°),如图 3,当 / / 时,求旋转
角 的度数;
(3)如图 4,等腰直角△ 的起始位置如图 4 所示,∠ = 45°,点 在 上,点 在 延长线上时,若
△ 固定不动,绕点 顺时针转动△ ,旋转角的度数小于 130°,则当△ 的三边依次与 平行时,
旋转角的度数为______.
第 5页,共 10页
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.3.5 × 10 5
12.0
13.16
14.17
15.92
16.3
17.解:(1)( 1)2024 + (2025 )0 ( 12 )
1
= 1 + 1 2
= 0;
(2)2024 × 2026 20252
= (2025 1) × (2025 + 1) 20252
= 20252 1 20252
= 1.
18.解:(1)8 5 ( )3 + ( 3 4)2
= 8 5 ( 3) + 9 8
= 8 8 + 9 8
= 8;
(2)( )( + 3 ) ( + )2
= 2 + 3 3 2 2 2 2
第 6页,共 10页
= 4 2.
19.解:(1) = 3① ,3 8 = 4②
由①,得 = 3 + ③,
把③代入②,得 3(3 + ) 8 = 4,
去括号,得 9 + 3 8 = 4,
解得: = 1,
把 = 1 代入③,得 = 3 + 1 = 4,
∴ = 4方程组的解为 = 1;
(2) 3 + 2 = 12①,
5 6 = 8②
① × 3,得 9 + 6 = 36③,
② +③,得 14 = 28,
解得: = 2,
把 = 2 代入①,得 3 × 2 + 2 = 12,
解得: = 3,
∴ = 2方程组的解为 = 3.
20.解:(1)由题意得,△ 向右平移 4 个单位长度,向上平移 1 个单位长度得到△ 1 1 1,
如图,△ 1 1 1和△ 2 2 2即为所求.
(2) △ 1 1 1与△ 2 2 2成中心对称.
如图,连接 1 2, 1 2, 1 2相交于点 ,
则点 即为所求.
(3)如图,取点 关于直线 的对称点 ′,连接 ′交直线 于点 ,连接 ,
此时△ 的周长为 + + = + + ′ = + ′,为最小值,
则点 即为所求.
第 7页,共 10页
21.解:(1)图形如图所示:
(2)共有 7 种涂法.
故答案为:7.
22.解:(1)设两个连续奇数是 2 + 1 和 2 1(其中 取正整数),
(2 + 1)2 (2 1)2
= 4 2 + 4 + 1 (4 2 4 + 1)
= 4 2 + 4 + 1 4 2 + 4 1
= 8 ,
当 8 = 32 时,
= 4,
2 + 1 = 9,
2 1 = 7,
32 = 92 72,32 是“好数”.
当 8 = 45 时,
= 5.625,(不符合题意,舍去).
答:32 是“好数”,32 = 92 72,45 不是好数.
(2)设两个连续奇数是 2 + 1 和 2 1(其中 取正整数),
(2 + 1)2 (2 1)2
= 4 2 + 4 + 1 (4 2 4 + 1)
= 4 2 + 4 + 1 4 2 + 4 1
= 8 .
答:由这两个连续奇数构造的“好数”是 8 .
23.解:(1)图 1 整体上是边长为 + 的正方形,因此面积为( + )2,拼成图 1 的四个部分的面积和为 2 +
2 + 2,
第 8页,共 10页
所以有( + )2 = 2 + 2 + 2,
故答案为:( + )2 = 2 + 2 + 2;
(2)图 2 中间小正方形的边长为 ,因此面积为( )2,中间小正方形的面积也可以看作大正方形面积
与四个长方形的面积差,即( + )2 4 ,
所以有( )2 = ( + )2 4 ,
故答案为:( )2 = ( + )2 4 ;
(3) ∵ + = 8, = 7,
∴ ( )2 = ( + )2 4 = 64 28 = 36,
∴ = 6 或 = 6;
(4)设正方形 的边长为 ,正方形 的边长为 ,
∵图甲和图乙中阴影部分的面积分别为 3 和 12,
∴ ( )2 = 3,( + )2 ( 2 + 2) = 12,即 = 6,
∴正方形 , 的面积之和为 2 + 2 = ( )2 + 2 = 3 + 12 = 15,
故答案为:15. .
24.解:(1)如图,
(2)如图, 与 交于点 ,
∵ ∠ = 60°, 平分∠ ,
∴ ∠ = 30°,
∴ ∠ = 60°,
∵ // ,
∴ ∠ = ∠ = 60°,
∵ ∠ = 45°,
第 9页,共 10页
∴ ∠ = 180° 45° 60° = 75°,
∴ ∠ = 90° 75° = 15°.
即旋转角 的度数为 15°;
(3)分三种情况:
当 // ,如图,
∵ // ,
∴ ∠ = ∠ = 30°,
即旋转角为 30°;
当 // 时,如图,
∵ ∠ = ∠ = 60°,∠ = ∠ = 45°,
∴ ∠ = 180° ∠ ∠ = 180° 45° 60° = 75°;
当 // 时,如图,
∴ ∠ = ∠ = 90° ∠ = 30°,
∴ ∠ = ∠ + ∠ = 90° + 30° = 120°;
综上所述,旋转角为 30°或 75°或 120°.
故答案为:30°或 75°或 120°
第 10页,共 10页
一、选择题:本题共 10小题,每小题 3分,共 30分。在每小题给出的选项中,只有一项是符合题目要求
的。
1.剪纸是中国独特的民间艺术,如图是我国传统文化中的“福禄寿喜”剪纸图,其中是中心对称图形的是
( )
A. B. C. D.
2.下列运算,结果正确的是( )
A. 3 2 = B. ( + )2 = 2 + 2
C. (3 3)2 = 9 6 D. ( 4)3 = 7
3 1.在方程2 = + 1,2 + 3 = 5,2 1 = , + = 0 中二元一次方程的个数为( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
4.下列四组数值是二元一次方程 2 + = 10 的解是( )
A. = 1 = 4 = 2 = 2 = 5 B. = 2 C. = 4 D. = 3
5.已知 = 8, = 16,则 的值为( )
A. 12 B. 6 C. 8 D. 2
6.已知 + = 5, = 3,则( + 1)( + 1) =( )
A. 3 B. 2 C. 3 D. 9
7.如( + )与( + 4)的乘积中不含 的一次项,则 的值为( )
A. 4 B. 4 C. 0 D. 1
8 1.计算( )20242 × 2
2025 × 3 的值等于( )
A. 3 B. 3 C. 6 D. 6
9.小芳和小明在手工课上各自制作楼梯模型(中间是空的),如下图,则他们所用的材料( )
A.一样长 B.小明的长 C.小芳的长 D.不能确定
第 1页,共 10页
10.如图,格点三角形甲逆时针旋转 90°后得到格点三角形乙,则其旋转中心是( )
A.点 B.点 C.点 D.点
二、填空题:本题共 6小题,每小题 3分,共 18分。
11.某微生物细胞直径为 0.000035 米,将 0.000035 用科学记数法表示为______.
12 = 2.已知 = 1是方程 + = 3 的解,则代数式 2 + 3 的值为______.
13.若 2 + 4 = 0,则22 × 2 = ______.
14.如图,等腰△ 中, = , = 14 ,点 是 的中点, = 5 ,将
线段 沿 方向平移 7 得到线段 ,点 、 分别落在边 、 上,则△
的周长是______ .
15.如图,在直角△ 中,∠ = 90°,分别以两直角边为腰作等腰直角三角形,
记 1 = △ , 2 = △ ,其中 1 + 2 = 9, = 6,则图中阴影部分面积为______.
16.有许多非常复杂的几何图形可以由简单的数学规则创造出来.比如谢尔宾斯基三角形,它的构造方法是:
以一个等边三角形为初始图形,每次将等边三角形分割成 4 个边长为原来一半的小三角形,并去掉其中间
的小三角形,将这个过程反复进行下去,就可以得到无限细节的谢尔宾斯基三角形,如图所示,按此规律,
第 个图形中剩余的三角形(黑色三角形)的个数为______.
三、解答题:本题共 8小题,共 72分。解答应写出文字说明,证明过程或演算步骤。
第 2页,共 10页
17.(本小题 8 分)
计算:
(1)( 1)2024 + (2025 )0 ( 1 ) 12 ;
(2)2024 × 2026 20252.
18.(本小题 10 分)
计算:
(1)8 5 ( )3 + ( 3 4)2;
(2)( )( + 3 ) ( + )2.
19.(本小题 10 分)
解二元一次方程组:
= 3
(1) 3 8 = 4;
3 + 2 = 12
(2) 5 6 = 8.
20.(本小题 8 分)
如图,在正方形网格中,每个小正方形的边长都是 1 个单位长度,△ 的三个顶点都在格点上.
(1)平移图中的△ ,使点 移到点 1的位置,画出平移后的△ 1 1 1;画出△ 关于点 成中心对称的
△ 2 2 2;
(2) △ 1 1 1与△ 2 2 2是否成中心对称?若是,画出其对称中心点 的位置;
(3)在直线 上找一点 ,使△ 的周长最小,请在图中标出点 的位置.
21.(本小题 8 分)
如图,是相同的小正方形拼成的正方形网格,其中的两个小正方形已涂色,请你在图中再涂两个小正方形,
并满足:①4 个涂色的小正方形中,每个小正方形至少与其余 3 个小正方形中的 1 个有公共点;②连同空
第 3页,共 10页
白小正方形一起构成轴对称图形,即阴影部分呈轴对称,空白部分也呈轴对称,且共用一条对称轴.
(1)在正方形网格中画出你的 3 种涂法;
(2)共有______种涂法. (8 个图不一定全用到)
22.(本小题 7 分)
如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“好数”.例如:因为 8 = 32 12,
16 = 52 32,24 = 72 52,所以 8,16,24 这三个数都是“好数”.
(1)32 和 45 这两个数是“好数”吗?若是,请表示成两个连续奇数的平方差形式;
(2)设两个连续奇数是 2 + 1 和 2 1(其中 取正整数),试求由这两个连续奇数构造的“好数”.
23.(本小题 10 分)
【知识生成】通过第八章的学习:我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得
到一个数学等式,请
结合图形解答下列
问题:
(1)写出图 1 中所表示的数学等式______;
(2)如图 2,是用 4 块完全相同的长方形拼成正方形,用两种不同的方法求图中阴影部分的面积,得到的数
学等式是______;
(3)【知识应用】
若 + = 8, = 7,求 的值;
(4)【灵活应用】
第 4页,共 10页
图 3 中有两个正方形 、 ,现将 放在 的内部得到图甲,将 、 并列放置后构造新的正方形得到图乙.若
图甲和图乙中阴影部分的面积分别为 3 和 12,则正方形 , 的面积之和是______.
24.(本小题 11 分)
如图,在直角△ 中,∠ = 90°,∠ = 60°.
(1)在图 1 中,用直尺和圆规作出∠ 的角平分线 ,交边 于点 ;(要求:尺规作图,保留作图痕迹,
不写作法)
(2)如图 2,在(1)的条件下,已知等腰直角三角形 ,∠ = 45°,点 在线段 上,且不与点 、 重合,
点 在 上,△ 固定不动,△ 绕点 顺时针旋转 (0 < < 90°),如图 3,当 / / 时,求旋转
角 的度数;
(3)如图 4,等腰直角△ 的起始位置如图 4 所示,∠ = 45°,点 在 上,点 在 延长线上时,若
△ 固定不动,绕点 顺时针转动△ ,旋转角的度数小于 130°,则当△ 的三边依次与 平行时,
旋转角的度数为______.
第 5页,共 10页
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.3.5 × 10 5
12.0
13.16
14.17
15.92
16.3
17.解:(1)( 1)2024 + (2025 )0 ( 12 )
1
= 1 + 1 2
= 0;
(2)2024 × 2026 20252
= (2025 1) × (2025 + 1) 20252
= 20252 1 20252
= 1.
18.解:(1)8 5 ( )3 + ( 3 4)2
= 8 5 ( 3) + 9 8
= 8 8 + 9 8
= 8;
(2)( )( + 3 ) ( + )2
= 2 + 3 3 2 2 2 2
第 6页,共 10页
= 4 2.
19.解:(1) = 3① ,3 8 = 4②
由①,得 = 3 + ③,
把③代入②,得 3(3 + ) 8 = 4,
去括号,得 9 + 3 8 = 4,
解得: = 1,
把 = 1 代入③,得 = 3 + 1 = 4,
∴ = 4方程组的解为 = 1;
(2) 3 + 2 = 12①,
5 6 = 8②
① × 3,得 9 + 6 = 36③,
② +③,得 14 = 28,
解得: = 2,
把 = 2 代入①,得 3 × 2 + 2 = 12,
解得: = 3,
∴ = 2方程组的解为 = 3.
20.解:(1)由题意得,△ 向右平移 4 个单位长度,向上平移 1 个单位长度得到△ 1 1 1,
如图,△ 1 1 1和△ 2 2 2即为所求.
(2) △ 1 1 1与△ 2 2 2成中心对称.
如图,连接 1 2, 1 2, 1 2相交于点 ,
则点 即为所求.
(3)如图,取点 关于直线 的对称点 ′,连接 ′交直线 于点 ,连接 ,
此时△ 的周长为 + + = + + ′ = + ′,为最小值,
则点 即为所求.
第 7页,共 10页
21.解:(1)图形如图所示:
(2)共有 7 种涂法.
故答案为:7.
22.解:(1)设两个连续奇数是 2 + 1 和 2 1(其中 取正整数),
(2 + 1)2 (2 1)2
= 4 2 + 4 + 1 (4 2 4 + 1)
= 4 2 + 4 + 1 4 2 + 4 1
= 8 ,
当 8 = 32 时,
= 4,
2 + 1 = 9,
2 1 = 7,
32 = 92 72,32 是“好数”.
当 8 = 45 时,
= 5.625,(不符合题意,舍去).
答:32 是“好数”,32 = 92 72,45 不是好数.
(2)设两个连续奇数是 2 + 1 和 2 1(其中 取正整数),
(2 + 1)2 (2 1)2
= 4 2 + 4 + 1 (4 2 4 + 1)
= 4 2 + 4 + 1 4 2 + 4 1
= 8 .
答:由这两个连续奇数构造的“好数”是 8 .
23.解:(1)图 1 整体上是边长为 + 的正方形,因此面积为( + )2,拼成图 1 的四个部分的面积和为 2 +
2 + 2,
第 8页,共 10页
所以有( + )2 = 2 + 2 + 2,
故答案为:( + )2 = 2 + 2 + 2;
(2)图 2 中间小正方形的边长为 ,因此面积为( )2,中间小正方形的面积也可以看作大正方形面积
与四个长方形的面积差,即( + )2 4 ,
所以有( )2 = ( + )2 4 ,
故答案为:( )2 = ( + )2 4 ;
(3) ∵ + = 8, = 7,
∴ ( )2 = ( + )2 4 = 64 28 = 36,
∴ = 6 或 = 6;
(4)设正方形 的边长为 ,正方形 的边长为 ,
∵图甲和图乙中阴影部分的面积分别为 3 和 12,
∴ ( )2 = 3,( + )2 ( 2 + 2) = 12,即 = 6,
∴正方形 , 的面积之和为 2 + 2 = ( )2 + 2 = 3 + 12 = 15,
故答案为:15. .
24.解:(1)如图,
(2)如图, 与 交于点 ,
∵ ∠ = 60°, 平分∠ ,
∴ ∠ = 30°,
∴ ∠ = 60°,
∵ // ,
∴ ∠ = ∠ = 60°,
∵ ∠ = 45°,
第 9页,共 10页
∴ ∠ = 180° 45° 60° = 75°,
∴ ∠ = 90° 75° = 15°.
即旋转角 的度数为 15°;
(3)分三种情况:
当 // ,如图,
∵ // ,
∴ ∠ = ∠ = 30°,
即旋转角为 30°;
当 // 时,如图,
∵ ∠ = ∠ = 60°,∠ = ∠ = 45°,
∴ ∠ = 180° ∠ ∠ = 180° 45° 60° = 75°;
当 // 时,如图,
∴ ∠ = ∠ = 90° ∠ = 30°,
∴ ∠ = ∠ + ∠ = 90° + 30° = 120°;
综上所述,旋转角为 30°或 75°或 120°.
故答案为:30°或 75°或 120°
第 10页,共 10页
同课章节目录
