10.1 课时2 垂线 课件(共19张PPT)2024-2025学年数学沪科版七年级下册
文档属性
| 名称 | 10.1 课时2 垂线 课件(共19张PPT)2024-2025学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 23:10:59 | ||
图片预览




文档简介
(共19张PPT)
10.1 相交线
课时2 垂线
1.理解垂线的有关概念及画法.
2.经历观察、操作、想象、概括、交流等过程,进一步发展空间观念. (重点、难点)
学习目标
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
课堂导入
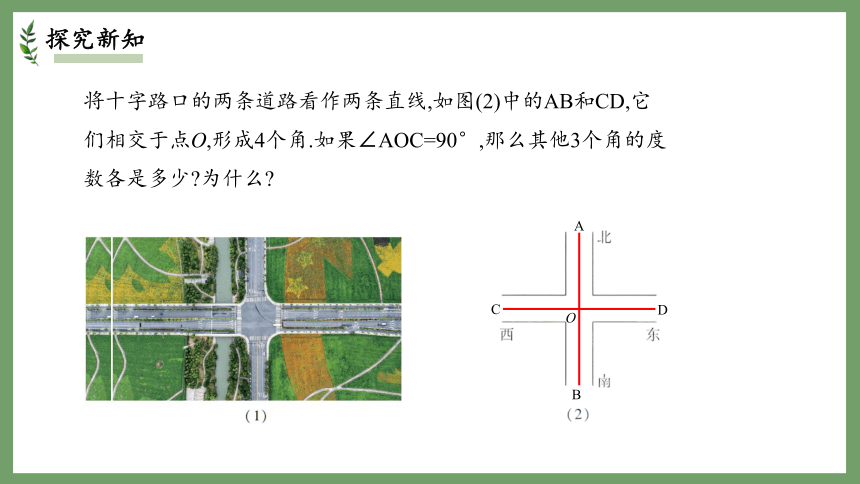
将十字路口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他3个角的度数各是多少 为什么
A
B
C
D
O
探究新知
A
B
C
D
O
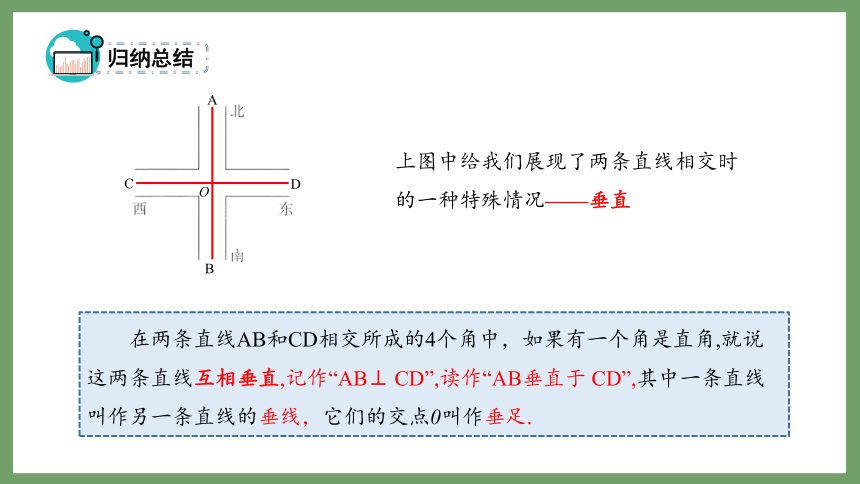
上图中给我们展现了两条直线相交时
的一种特殊情况——垂直
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥ CD”,读作“AB垂直于 CD”,其中一条直线叫作另一条直线的垂线,它们的交点0叫作垂足.
归纳总结
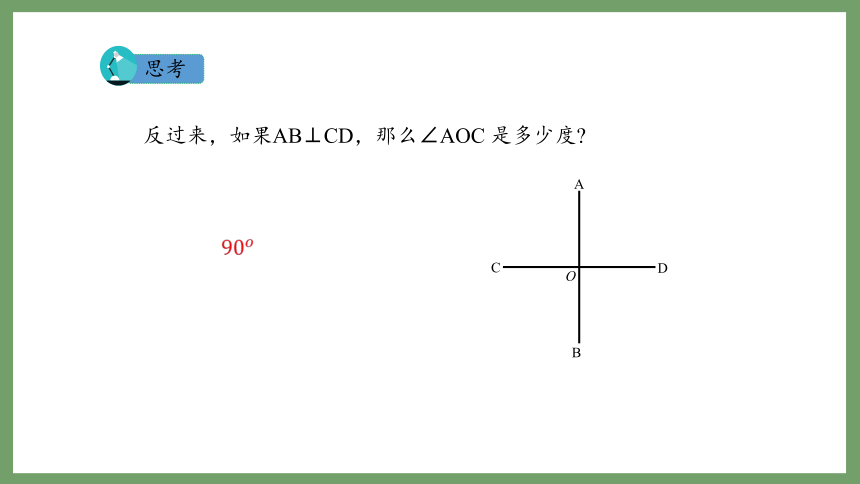
思考
反过来,如果AB⊥CD,那么∠AOC 是多少度
A
B
C
D
O
如图,当直线AB与CD相交于O点,
∠AOC=AB⊥CD,垂足为O.
几何语言:
因为∠AOC=
所以AB⊥CD(垂直的定义)
垂直的书写形式:
A
B
C
D
O
反之,若直线AB与CD垂直,垂足为O.∠AOC=
几何语言:
因为AB⊥CD(已知)
所以∠AOC=(垂直的定义)
∠BOC=∠AOD=∠BOD=
垂直的书写形式:
A
B
C
D
O
生活中两条直线垂直图形:
你能再举出生活中一些两条直线互相垂直的例子吗
思考
1.如图1,若直线m、n相交于点O,∠1=,则 ;
2.若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD =______;
O
m
n
1
图1
C
m⊥n
练一练
3.如图,直线AB与CD相交于点O,且∠AOC =∠BOC.那么直线AB与 CD有什么位置关系 为什么
A
B
C
D
O
解:AB⊥CD
因为∠AOC ∠BOC=
∠AOC =∠BOC
所以2∠AOC= 即∠AOC=
所以AB⊥CD
1.用折纸方法画垂线
如图中所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线
动手操作
l
P
2.用三角板画垂线
如图,过已知直线l上(或外)的一点P画直线,使它与直线l垂直.
1.点P在直线l上
一靠:把三角尺的一条直角边靠着已知直线
二移:沿着直线移动三角尺,让另一条直角边靠住已知点P
三画:沿这条直角边画直线
四标:标上直角符号
2.点P在直线l外
l
P
通过上面的操作,你知道过一点画已知直线的垂线,能画几条吗
能作一条,而且只能作一条.
关于直线的垂线,有如下基本事实:
同一平面内,过一点有且只有一条直线与己知直线垂直.
归纳总结
1.如图,在三角形ABC中,D是BC 中点,连接AD,请分别画出自点B, 点C向AD 所作的垂线(垂足为点E,F)
A
B
C
D
练一练
1.两条直线相交所成的四个角中,下列条件中能判定
两条直线垂直的是( )
A. 有两个角相等
B.有两对角相等
C. 有三个角相等
D.有四对邻补角
C
当堂检测
2.如图,O是直线AB上的一点,∠AOC= ∠BOC,OC是∠AOD的平分线.判断OD与AB的位置关系,并说明理由.
解:OD⊥AB 理由如下:
因为∠COD =∠AOC=
所以∠AOD=∠AOC∠COD=
所以OD⊥AB
A
B
D
O
C
3.如图,分别过点P作直线AB的垂线.
P
P
A
B
A
B
P
A
B
垂线
概念
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直
课堂小结
画法
用折纸方法画垂线
用三角板画垂线
记作“AB⊥ CD”,读作“AB垂直于 CD”
关于直线的垂线,基本事实:
同一平面内,过一点有且只有一条直线与己知直线垂直.
10.1 相交线
课时2 垂线
1.理解垂线的有关概念及画法.
2.经历观察、操作、想象、概括、交流等过程,进一步发展空间观念. (重点、难点)
学习目标
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
课堂导入
将十字路口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他3个角的度数各是多少 为什么
A
B
C
D
O
探究新知
A
B
C
D
O
上图中给我们展现了两条直线相交时
的一种特殊情况——垂直
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥ CD”,读作“AB垂直于 CD”,其中一条直线叫作另一条直线的垂线,它们的交点0叫作垂足.
归纳总结
思考
反过来,如果AB⊥CD,那么∠AOC 是多少度
A
B
C
D
O
如图,当直线AB与CD相交于O点,
∠AOC=AB⊥CD,垂足为O.
几何语言:
因为∠AOC=
所以AB⊥CD(垂直的定义)
垂直的书写形式:
A
B
C
D
O
反之,若直线AB与CD垂直,垂足为O.∠AOC=
几何语言:
因为AB⊥CD(已知)
所以∠AOC=(垂直的定义)
∠BOC=∠AOD=∠BOD=
垂直的书写形式:
A
B
C
D
O
生活中两条直线垂直图形:
你能再举出生活中一些两条直线互相垂直的例子吗
思考
1.如图1,若直线m、n相交于点O,∠1=,则 ;
2.若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD =______;
O
m
n
1
图1
C
m⊥n
练一练
3.如图,直线AB与CD相交于点O,且∠AOC =∠BOC.那么直线AB与 CD有什么位置关系 为什么
A
B
C
D
O
解:AB⊥CD
因为∠AOC ∠BOC=
∠AOC =∠BOC
所以2∠AOC= 即∠AOC=
所以AB⊥CD
1.用折纸方法画垂线
如图中所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线
动手操作
l
P
2.用三角板画垂线
如图,过已知直线l上(或外)的一点P画直线,使它与直线l垂直.
1.点P在直线l上
一靠:把三角尺的一条直角边靠着已知直线
二移:沿着直线移动三角尺,让另一条直角边靠住已知点P
三画:沿这条直角边画直线
四标:标上直角符号
2.点P在直线l外
l
P
通过上面的操作,你知道过一点画已知直线的垂线,能画几条吗
能作一条,而且只能作一条.
关于直线的垂线,有如下基本事实:
同一平面内,过一点有且只有一条直线与己知直线垂直.
归纳总结
1.如图,在三角形ABC中,D是BC 中点,连接AD,请分别画出自点B, 点C向AD 所作的垂线(垂足为点E,F)
A
B
C
D
练一练
1.两条直线相交所成的四个角中,下列条件中能判定
两条直线垂直的是( )
A. 有两个角相等
B.有两对角相等
C. 有三个角相等
D.有四对邻补角
C
当堂检测
2.如图,O是直线AB上的一点,∠AOC= ∠BOC,OC是∠AOD的平分线.判断OD与AB的位置关系,并说明理由.
解:OD⊥AB 理由如下:
因为∠COD =∠AOC=
所以∠AOD=∠AOC∠COD=
所以OD⊥AB
A
B
D
O
C
3.如图,分别过点P作直线AB的垂线.
P
P
A
B
A
B
P
A
B
垂线
概念
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直
课堂小结
画法
用折纸方法画垂线
用三角板画垂线
记作“AB⊥ CD”,读作“AB垂直于 CD”
关于直线的垂线,基本事实:
同一平面内,过一点有且只有一条直线与己知直线垂直.
