10.2 课时3 平行线的判定方法 课件(共18张PPT)
文档属性
| 名称 | 10.2 课时3 平行线的判定方法 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 901.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
10.2 平行线的判定
10.2 课时3 平行线的判定方法
1.掌握两条直线平行的方法,能运用平行线的判定方法进行简单的推理论证;
2.通过对两条直线平行条件的探索,理解两直线平行的条件.
在同一平面内,如果两条直线不相交的叫做_______.
平行线
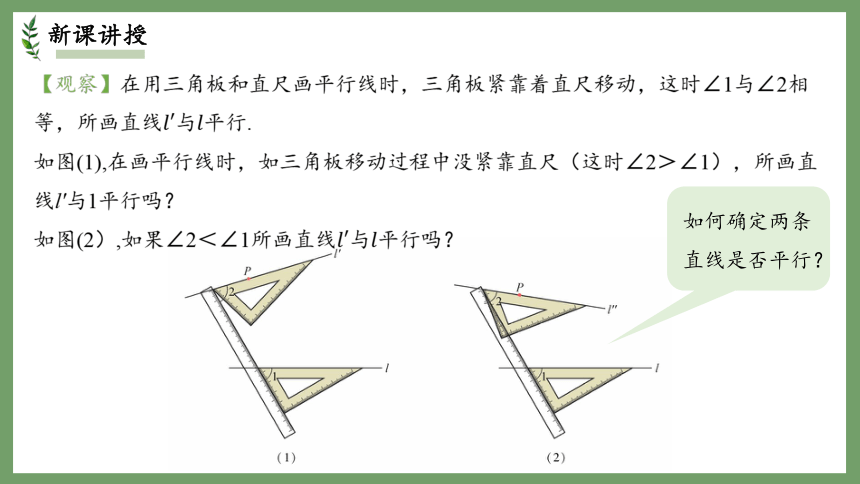
【问题1】但由于直线是无限延伸的,检验它们是否相交有困难,难以直接判断,那么有没有其他判定方法呢?
b
a
如何确定两条直线是否平行?
【观察】在用三角板和直尺画平行线时,三角板紧靠着直尺移动,这时∠1与∠2相等,所画直线与平行.
如图(1),在画平行线时,如三角板移动过程中没紧靠直尺(这时∠2>∠1),所画直线l'与1平行吗?
如图(2),如果∠2<∠1所画直线与平行吗?
1
2
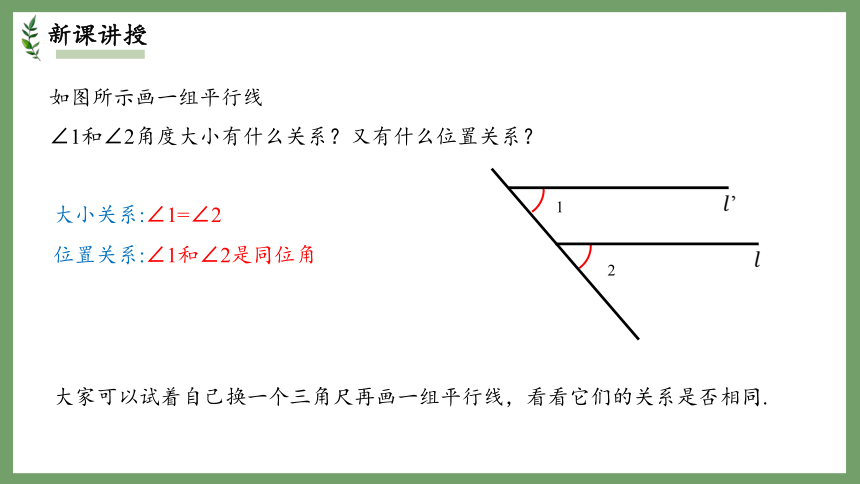
大小关系:∠1=∠2
位置关系:∠1和∠2是同位角
大家可以试着自己换一个三角尺再画一组平行线,看看它们的关系是否相同.
如图所示画一组平行线
∠1和∠2角度大小有什么关系?又有什么位置关系?
’
如图所示画一组平行线
∠1和∠2角度大小有什么关系?又有什么位置关系?
大小关系:∠1=∠2
位置关系:∠1和∠2是同位角
可以看出,同位角∠1和∠2是否相等,决定了直线与是否平行.由此我们得到如下基本事实:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成
同位角相等,两直线平行.
’
1
2
例1 已知:直线AB和点C,点C在直线AB外. 求作:直线CD,使直线CD//AB.
分析:根据“同位角相等,两直线平行”,可将作平行线的问题转化为作角相等的问题.因此,过点C作一条直线与AB相交(作截线),然后作一对同位角相等即可.
作法:
1.如图,过点C作直线EF交AB于点F.
2.以点C为顶点,CE为边,在EF的右侧作∠ECD=∠EFB.
3.作直线CD,直线CD就是所求作的直线.
a
b
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a//b吗?
1
2
理由如下:
因为 ∠1=∠4, ∠1=∠2( )
所以 ∠2=∠4
c
3
4
?
对顶角相等
所以当 时, a∥b
∠2=∠4
解:如果 ∠2=∠4,由判定方法1,能得到a∥b,
a
b
1
2
c
3
4
由于∠2与∠4属于内错角,就得到了利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成
内错角相等,两直线平行.
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a//b吗?
思考
a
b
【问题】两条直线被第三条直线所截,同时能得到______、______和________.由同位角和内错角相等,可以判定两条直线平行,能否利用同旁内角来判定两条直线平行呢?
1
2
(1)同旁内角∠3和∠4满足什么条件时,能得出a∥b?
c
同位角
内错角
同旁内角
3
4
解: 如果 ∠3+∠4=180°,由判定方法2,能得到a∥b,理由如下:
因为 ∠1+∠3=180°,∠2+∠3=180°
所以 ∠4=∠2
所以 a∥b
(内错角相等,两直线平行.)
a
b
【问题】两条直线被第三条直线所截,同时能得到______、______和__________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
由于∠3与∠4属于同旁内角,就得到了利用同旁内角判定两条直线平行的方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成
同旁内角互补,两直线平行.
(1)同旁内角∠3和∠4满足什么条件时,能得出a∥b?
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗 为什么
a
b
c
1
2
解:这两条直线平行,理由如下:
如图
因为b⊥a,所以∠1=90°
同理∠2=90°,所以∠1=∠2
又因为∠1和∠2是同位角
所以b∥c
分析:垂直总与直角联系在一起,进而可以用相应角的关系来判断两条直线是否平行.
1.在使用平行线的判定方法时,要明确以下两点:
(1)各判定方法的条件是什么,结论是什么,
(2)判定方法已知的是角的关系,说明的是两直线平行
2.在使用平行线的判定方法时,碰到复杂图形要会从其中分离出基本图形.
3.在同一平面内,垂直于同一条直线的两条直线平行
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行.
平行线的判定方法
1、如图,完成下面的练习:
若∠1=∠2,则b__c.
若∠1=∠2,则___∥____.
若∠___=∠___,则AB∥DC.
(1)
(2)
∥
AD
BC
2
3
查漏补缺
2、如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行 为什么
(2)如果∠D=∠DCG,可以判断哪两条直线平行 为什么
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行 为什么
(3)AD//EF,同旁内角互补,两直线平行.
解:(1)AB//CD,同位角相等,两直线平行;
(2)AD//BC,内错角相等,两直线平行;
查漏补缺
3、如图,∠1=∠2能判断AB∥DF吗 为什么
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢 写出这个条件,并说明你的理由
解:不能
添加∠ CBD= ∠ EDB
内错角相等,两直线平行
想想还可以添加什么条件
查漏补缺
4、如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,那么a与c平行吗?为什么?
a
b
c
d
e
1
2
3
4
解:a与c平行,理由如下:
因为∠1=∠2(已知)
所以a∥b(内错角相等,两直线平行)
又因为∠3+∠4=180°(已知)
所以c∥b(同旁内角相等,两直线平行)
因为a∥b,c∥b
所以 a∥c
能力提升
10.2 平行线的判定
10.2 课时3 平行线的判定方法
1.掌握两条直线平行的方法,能运用平行线的判定方法进行简单的推理论证;
2.通过对两条直线平行条件的探索,理解两直线平行的条件.
在同一平面内,如果两条直线不相交的叫做_______.
平行线
【问题1】但由于直线是无限延伸的,检验它们是否相交有困难,难以直接判断,那么有没有其他判定方法呢?
b
a
如何确定两条直线是否平行?
【观察】在用三角板和直尺画平行线时,三角板紧靠着直尺移动,这时∠1与∠2相等,所画直线与平行.
如图(1),在画平行线时,如三角板移动过程中没紧靠直尺(这时∠2>∠1),所画直线l'与1平行吗?
如图(2),如果∠2<∠1所画直线与平行吗?
1
2
大小关系:∠1=∠2
位置关系:∠1和∠2是同位角
大家可以试着自己换一个三角尺再画一组平行线,看看它们的关系是否相同.
如图所示画一组平行线
∠1和∠2角度大小有什么关系?又有什么位置关系?
’
如图所示画一组平行线
∠1和∠2角度大小有什么关系?又有什么位置关系?
大小关系:∠1=∠2
位置关系:∠1和∠2是同位角
可以看出,同位角∠1和∠2是否相等,决定了直线与是否平行.由此我们得到如下基本事实:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成
同位角相等,两直线平行.
’
1
2
例1 已知:直线AB和点C,点C在直线AB外. 求作:直线CD,使直线CD//AB.
分析:根据“同位角相等,两直线平行”,可将作平行线的问题转化为作角相等的问题.因此,过点C作一条直线与AB相交(作截线),然后作一对同位角相等即可.
作法:
1.如图,过点C作直线EF交AB于点F.
2.以点C为顶点,CE为边,在EF的右侧作∠ECD=∠EFB.
3.作直线CD,直线CD就是所求作的直线.
a
b
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a//b吗?
1
2
理由如下:
因为 ∠1=∠4, ∠1=∠2( )
所以 ∠2=∠4
c
3
4
?
对顶角相等
所以当 时, a∥b
∠2=∠4
解:如果 ∠2=∠4,由判定方法1,能得到a∥b,
a
b
1
2
c
3
4
由于∠2与∠4属于内错角,就得到了利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成
内错角相等,两直线平行.
如图,直线a,b被直线c所截,如果内错角∠2和∠4相等,你能根据上面的基本事实,说明直线a//b吗?
思考
a
b
【问题】两条直线被第三条直线所截,同时能得到______、______和________.由同位角和内错角相等,可以判定两条直线平行,能否利用同旁内角来判定两条直线平行呢?
1
2
(1)同旁内角∠3和∠4满足什么条件时,能得出a∥b?
c
同位角
内错角
同旁内角
3
4
解: 如果 ∠3+∠4=180°,由判定方法2,能得到a∥b,理由如下:
因为 ∠1+∠3=180°,∠2+∠3=180°
所以 ∠4=∠2
所以 a∥b
(内错角相等,两直线平行.)
a
b
【问题】两条直线被第三条直线所截,同时能得到______、______和__________.由同位角相等,可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
1
2
c
同位角
内错角
同旁内角
3
4
由于∠3与∠4属于同旁内角,就得到了利用同旁内角判定两条直线平行的方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成
同旁内角互补,两直线平行.
(1)同旁内角∠3和∠4满足什么条件时,能得出a∥b?
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗 为什么
a
b
c
1
2
解:这两条直线平行,理由如下:
如图
因为b⊥a,所以∠1=90°
同理∠2=90°,所以∠1=∠2
又因为∠1和∠2是同位角
所以b∥c
分析:垂直总与直角联系在一起,进而可以用相应角的关系来判断两条直线是否平行.
1.在使用平行线的判定方法时,要明确以下两点:
(1)各判定方法的条件是什么,结论是什么,
(2)判定方法已知的是角的关系,说明的是两直线平行
2.在使用平行线的判定方法时,碰到复杂图形要会从其中分离出基本图形.
3.在同一平面内,垂直于同一条直线的两条直线平行
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行.
平行线的判定方法
1、如图,完成下面的练习:
若∠1=∠2,则b__c.
若∠1=∠2,则___∥____.
若∠___=∠___,则AB∥DC.
(1)
(2)
∥
AD
BC
2
3
查漏补缺
2、如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行 为什么
(2)如果∠D=∠DCG,可以判断哪两条直线平行 为什么
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行 为什么
(3)AD//EF,同旁内角互补,两直线平行.
解:(1)AB//CD,同位角相等,两直线平行;
(2)AD//BC,内错角相等,两直线平行;
查漏补缺
3、如图,∠1=∠2能判断AB∥DF吗 为什么
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢 写出这个条件,并说明你的理由
解:不能
添加∠ CBD= ∠ EDB
内错角相等,两直线平行
想想还可以添加什么条件
查漏补缺
4、如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,那么a与c平行吗?为什么?
a
b
c
d
e
1
2
3
4
解:a与c平行,理由如下:
因为∠1=∠2(已知)
所以a∥b(内错角相等,两直线平行)
又因为∠3+∠4=180°(已知)
所以c∥b(同旁内角相等,两直线平行)
因为a∥b,c∥b
所以 a∥c
能力提升
