10.3 平行线的性质 课件(13张PPT)2024-2025学年数学沪科版七年级下册
文档属性
| 名称 | 10.3 平行线的性质 课件(13张PPT)2024-2025学年数学沪科版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 826.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 10:31:27 | ||
图片预览




文档简介
(共13张PPT)
10.3 平行线的性质
1.经历探索平行线的性质的过程,掌握平行线的性质,并能运用它们进行简单的推理和计算;
2.通过观察、操作、推理、交流等活动,发展学生的推理能力,进一步增强分析、概括和表达能力,提高学生对简单几何图形的感知能力.
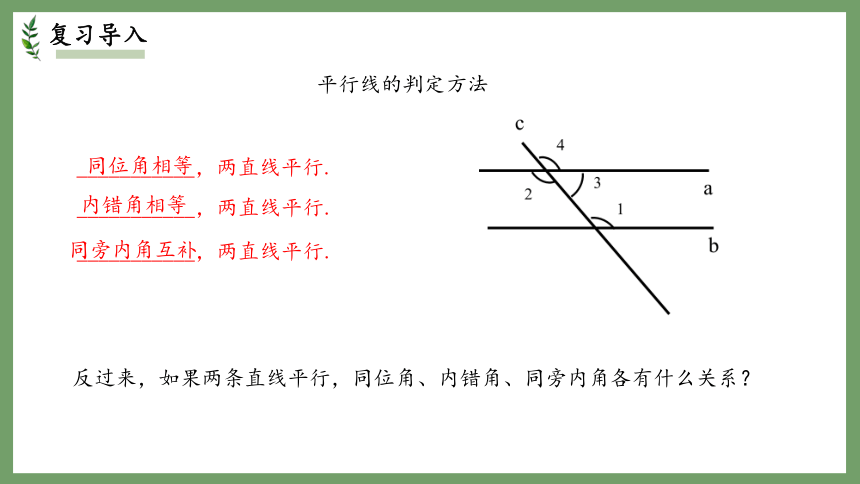
___________,两直线平行.
___________,两直线平行.
___________,两直线平行.
平行线的判定方法
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系?
同位角相等
内错角相等
同旁内角互补
【观察】如图,练习本上的横线都是相互平行的,从中任选两条分别记为AB,CD;画一条直线EF分别与AB,CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),量一量它们的度数,它们的大小有什么关系?由此你能得到什么结论
∠1=∠5
∠2=∠6
猜想:两条平行直线被第三条直线所截,同位角____.
相等
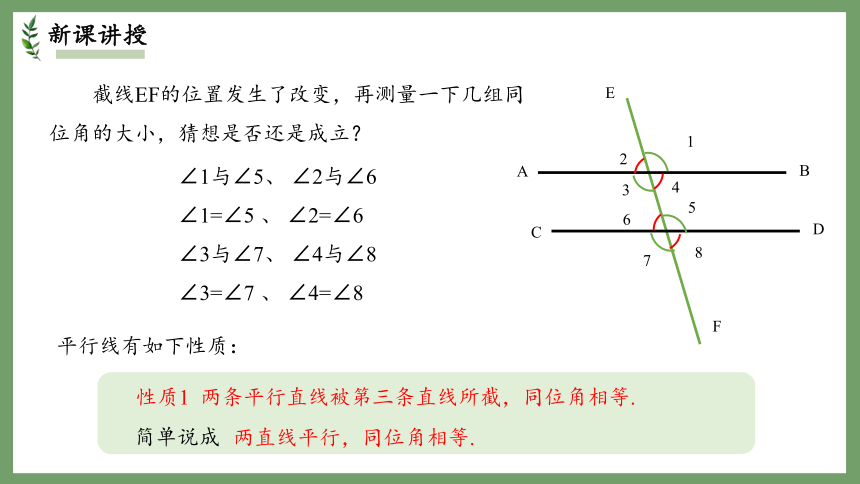
截线EF的位置发生了改变,再测量一下几组同位角的大小,猜想是否还是成立?
E
F
D
C
B
A
2
1
3
4
5
6
7
8
∠1与∠5、 ∠2与∠6
∠1=∠5 、 ∠2=∠6
∠3与∠7、 ∠4与∠8
∠3=∠7 、 ∠4=∠8
性质1 两条平行直线被第三条直线所截,同位角相等.
简单说成
两直线平行,同位角相等.
平行线有如下性质:
解:如图所示直线AB∥BC,EF是截线
因为 AB∥BC
所以 ∠1=∠5(两直线平行,同位角相等)
又因为 ∠1=∠3(对顶角相等)
所以 ∠3=∠5(等量代换)
【探究】如右图所示,当AB//CD时,内错角∠3与∠5的大小有什么关系?同旁内角∠4与∠5之间又有什么关系?请说明理由.
性质2 两条平行直线被第三条直线所截,内错角相等.
简单说成
两直线平行,内错角相等.
解:如图所示直线a∥b,c是截线
因为 a∥b
所以 ∠1=∠2(两直线平行,同位角相等)
又因为 ∠2+∠4=180°
所以 ∠1+∠4=180°(等量代换)
类似地,由性质1或性质2,可以推出平行线关于同旁内角的性质.
性质3 两条平行直线被第三条直线所截,同旁内角互补.
简单说成
两直线平行,同旁内角互补.
例 如图,已知点D,E,F分别在三角形ABC的边AB,AC,BC上,且DE//BC,B=48°.
(1)求∠ADE的度数;
(2)若FD是∠BFE 的平分线,且EF//AB.求∠EDF 的度数.
解:(1)因为DE//BC,
所以∠ADE=∠B=48°.
例 如图,已知点D,E,F分别在三角形ABC的边AB,AC,BC上,且DE//BC,B=48°.
(1)求∠ADE的度数;
(2)若FD是∠BFE 的平分线,且EF//AB.求∠EDF 的度数.
解:(2)因为FD平分∠BFE,所以∠BFD=∠EFD=∠BFE.
由EF//AB,
得∠B+∠BFE=180°,且∠BFD= ∠BFE,即∠B+2∠BFD=180°.
因为∠B=48°,所以∠BFD=66°.
因为DE//BC,所以∠EDF=∠BFD =66°.
性质1 性质2 性质3
平行线的性质 两直线平行 同位角相等 两直线平行 内错相等 两直线平行
同旁内角互补
图例
符号语言 ∵a∥b ∴∠1=∠2 ∵a∥b ∴∠2=∠3 ∵a∥b
∴∠2+∠4=180°
1、看图填空
(1)由 DE//BC,可以得到∠ADE=_______,
依据是_____________________.
(2)由DE//BC,可以得到∠DFB=_______,
依据是_____________________.
(3)由 DE//BC,可以得到∠C+=_______=180°,
依据是__________________________.
两直线平行 同位角相等
∠ABC
查漏补缺
∠FDE
两直线平行 内错角相等
∠DEC
两直线平行 同旁内角互补
2.有这样一道题:如图,若AB∥DE,AC∥DF,试说明∠A+∠D=180°.请补全下面的解答过程,括号内填写依据解.
解:因为 AB ∥ DE( )
所以 ∠A=∠CPD
( )
又因为 AC∥DF( )
所以 ∠D+∠CPD =180°
( )
因为 ∠A+∠D=180( )
已知
两直线平行,同位角相等
已知
两直线平行,同旁内角互补
等量代换
A
B
C
D
E
F
P
查漏补缺
3、已知:AB∥CD,试说明∠P,∠A,∠C的关系.
借助辅助线
解:过点P做AB,CD的平行线EF
因为 AB∥EF∥CD
所以 ∠A=∠APF,∠C=∠CPF
(两直线平行,内错角相等)
又因为 ∠P=∠APF+CPF
所以 ∠P=∠A+∠C(等量代换)
F
提升能力
10.3 平行线的性质
1.经历探索平行线的性质的过程,掌握平行线的性质,并能运用它们进行简单的推理和计算;
2.通过观察、操作、推理、交流等活动,发展学生的推理能力,进一步增强分析、概括和表达能力,提高学生对简单几何图形的感知能力.
___________,两直线平行.
___________,两直线平行.
___________,两直线平行.
平行线的判定方法
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系?
同位角相等
内错角相等
同旁内角互补
【观察】如图,练习本上的横线都是相互平行的,从中任选两条分别记为AB,CD;画一条直线EF分别与AB,CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),量一量它们的度数,它们的大小有什么关系?由此你能得到什么结论
∠1=∠5
∠2=∠6
猜想:两条平行直线被第三条直线所截,同位角____.
相等
截线EF的位置发生了改变,再测量一下几组同位角的大小,猜想是否还是成立?
E
F
D
C
B
A
2
1
3
4
5
6
7
8
∠1与∠5、 ∠2与∠6
∠1=∠5 、 ∠2=∠6
∠3与∠7、 ∠4与∠8
∠3=∠7 、 ∠4=∠8
性质1 两条平行直线被第三条直线所截,同位角相等.
简单说成
两直线平行,同位角相等.
平行线有如下性质:
解:如图所示直线AB∥BC,EF是截线
因为 AB∥BC
所以 ∠1=∠5(两直线平行,同位角相等)
又因为 ∠1=∠3(对顶角相等)
所以 ∠3=∠5(等量代换)
【探究】如右图所示,当AB//CD时,内错角∠3与∠5的大小有什么关系?同旁内角∠4与∠5之间又有什么关系?请说明理由.
性质2 两条平行直线被第三条直线所截,内错角相等.
简单说成
两直线平行,内错角相等.
解:如图所示直线a∥b,c是截线
因为 a∥b
所以 ∠1=∠2(两直线平行,同位角相等)
又因为 ∠2+∠4=180°
所以 ∠1+∠4=180°(等量代换)
类似地,由性质1或性质2,可以推出平行线关于同旁内角的性质.
性质3 两条平行直线被第三条直线所截,同旁内角互补.
简单说成
两直线平行,同旁内角互补.
例 如图,已知点D,E,F分别在三角形ABC的边AB,AC,BC上,且DE//BC,B=48°.
(1)求∠ADE的度数;
(2)若FD是∠BFE 的平分线,且EF//AB.求∠EDF 的度数.
解:(1)因为DE//BC,
所以∠ADE=∠B=48°.
例 如图,已知点D,E,F分别在三角形ABC的边AB,AC,BC上,且DE//BC,B=48°.
(1)求∠ADE的度数;
(2)若FD是∠BFE 的平分线,且EF//AB.求∠EDF 的度数.
解:(2)因为FD平分∠BFE,所以∠BFD=∠EFD=∠BFE.
由EF//AB,
得∠B+∠BFE=180°,且∠BFD= ∠BFE,即∠B+2∠BFD=180°.
因为∠B=48°,所以∠BFD=66°.
因为DE//BC,所以∠EDF=∠BFD =66°.
性质1 性质2 性质3
平行线的性质 两直线平行 同位角相等 两直线平行 内错相等 两直线平行
同旁内角互补
图例
符号语言 ∵a∥b ∴∠1=∠2 ∵a∥b ∴∠2=∠3 ∵a∥b
∴∠2+∠4=180°
1、看图填空
(1)由 DE//BC,可以得到∠ADE=_______,
依据是_____________________.
(2)由DE//BC,可以得到∠DFB=_______,
依据是_____________________.
(3)由 DE//BC,可以得到∠C+=_______=180°,
依据是__________________________.
两直线平行 同位角相等
∠ABC
查漏补缺
∠FDE
两直线平行 内错角相等
∠DEC
两直线平行 同旁内角互补
2.有这样一道题:如图,若AB∥DE,AC∥DF,试说明∠A+∠D=180°.请补全下面的解答过程,括号内填写依据解.
解:因为 AB ∥ DE( )
所以 ∠A=∠CPD
( )
又因为 AC∥DF( )
所以 ∠D+∠CPD =180°
( )
因为 ∠A+∠D=180( )
已知
两直线平行,同位角相等
已知
两直线平行,同旁内角互补
等量代换
A
B
C
D
E
F
P
查漏补缺
3、已知:AB∥CD,试说明∠P,∠A,∠C的关系.
借助辅助线
解:过点P做AB,CD的平行线EF
因为 AB∥EF∥CD
所以 ∠A=∠APF,∠C=∠CPF
(两直线平行,内错角相等)
又因为 ∠P=∠APF+CPF
所以 ∠P=∠A+∠C(等量代换)
F
提升能力
