江苏省盐城市建湖县第二中学2015-2016学年高二5月阶段考试数学试题
文档属性
| 名称 | 江苏省盐城市建湖县第二中学2015-2016学年高二5月阶段考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 528.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-31 00:00:00 | ||
图片预览




文档简介
建湖县第二中学高二数学独立练习
时间:120分钟
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.命题“,”的否定是 ▲ .
2.设复数满足(为虚数单位),则的实部为 ▲ .
3.某校高一年级有400人,高二年级有600人,高三年级有500人,现要采取分层抽样的方法从全校学生中选出100名学生进行问卷调查,那么抽出的样本中高二年级的学生人数为 ▲ .
4.“”是“”的 ▲ 条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个填空).
5.一个盒子中放有大小相同的3个白球和1个黑球,从中任取两个球,则所取的两个球不同色的概率为 ▲ .
6.根据如图所示的伪代码,可知输出的S的值为 ▲ .
7.在平面直角坐标系中,已知中心在坐标原点的双曲线经过点,且它的右焦点与抛物线的焦点相同,则该双曲线的标准方程
为 ▲ .
8.已知点在不等式组所表示
的平面区域内,则 的最大值为 ▲ .
9.已知,,,….,
类比这些等式,若(均为正实数),则= ▲ .
10.(理科学生做)已知展开式中所有项的二项式系数和为32,则其展开式中的常数项为 ▲ .
(文科学生做)已知平面向量满足,,,则向量夹角的余弦值为 ▲ .
11.(理科学生做)现从8名学生中选出4人去参加一项活动,若甲、乙两名同学不能同时入选,则共有 ▲ 种不同的选派方案.(用数字作答)
(文科学生做)设函数是奇函数,则实数的值为 ▲ .
12.设正实数满足,则当取得最大值时,的值为
▲ .
13.若函数在上单调递增,则实数的取值范围是 ▲ .
14.设点为函数与图象的公共点,以为切点可作直线与两曲线都相切,则实数的最大值为 ▲ .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
(理科学生做)设某地区型血的人数占总人口数的比为,现从中随机抽取3人.
(1)求3人中恰有2人为型血的概率;
(2)记型血的人数为,求的概率分布与数学期望.
(文科学生做)给定两个命题,:对任意实数都有恒成立;:.如果为真命题,为假命题,求实数的取值范围.
16.(本小题满分14分)
(理科学生做)设数列满足,.
(1)求;
(2)先猜想出的一个通项公式,再用数学归纳法证明你的猜想.
(文科学生做)已知函数()的一段图象如图所示.
(1)求函数的解析式;
(2)求函数的单调增区间;
(3)若,求函数的值域.
17.(本小题满分14分)
(理科学生做)如图,在直三棱柱中,,分别是的中点,且.
(1)求直线与所成角的大小;
(2)求直线与平面所成角的正弦值.
(文科学生做)设函数.
(1)用反证法证明:函数不可能为偶函数;
(2)求证:函数在上单调递减的充要条件是.
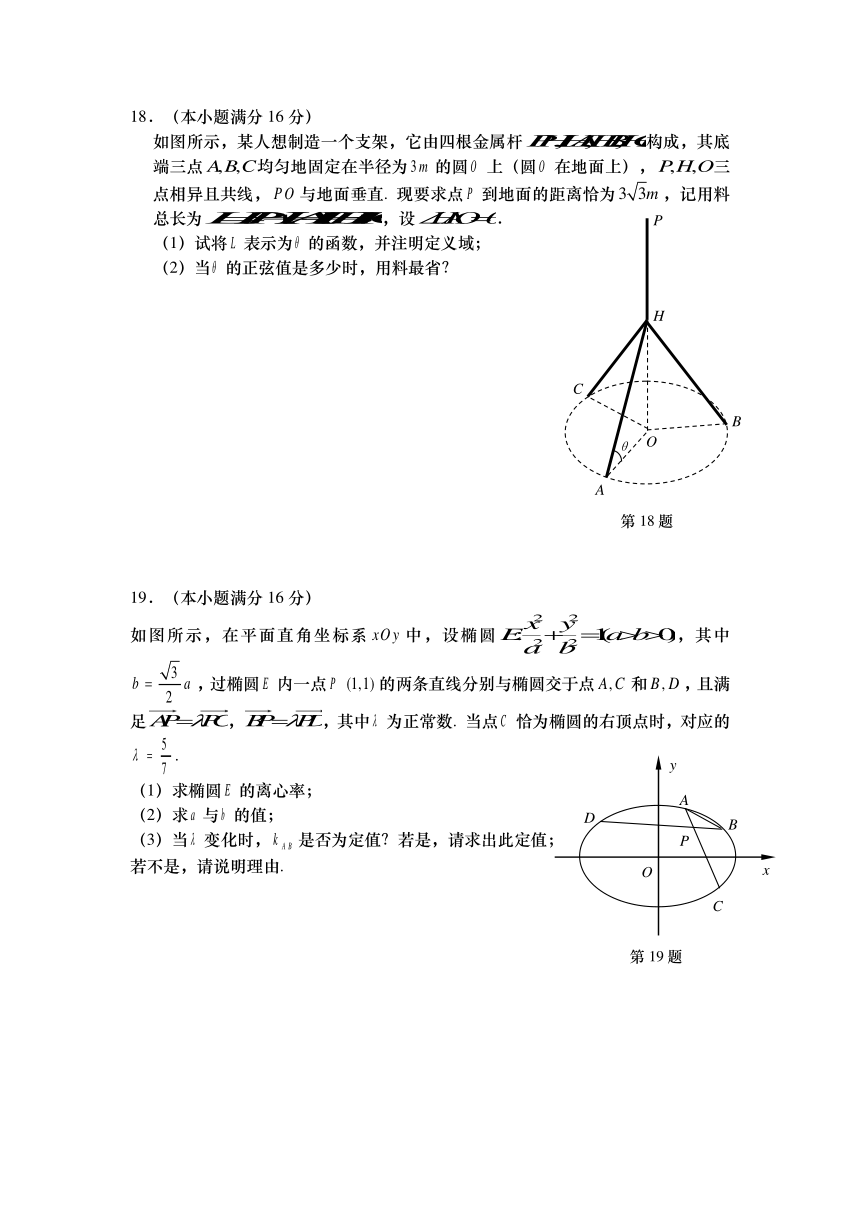
18.(本小题满分16分)
如图所示,某人想制造一个支架,它由四根金属杆构成,其底端三点均匀地固定在半径为的圆上(圆在地面上),三点相异且共线,与地面垂直. 现要求点到地面的距离恰为,记用料总长为,设.
(1)试将表示为的函数,并注明定义域;
(2)当的正弦值是多少时,用料最省?
19.(本小题满分16分)
如图所示,在平面直角坐标系中,设椭圆,其中,过椭圆内一点的两条直线分别与椭圆交于点和,且满足,,其中为正常数. 当点恰为椭圆的右顶点时,对应的.
(1)求椭圆的离心率;
(2)求与的值;
(3)当变化时,是否为定值?若是,请求出此定值;
若不是,请说明理由.
20.(本小题满分16分)
设函数.
(1)当时,求函数的极大值;
(2)若函数的图象与函数的图象有三个不同的交点,求的取值范围;
(3)设,当时,求函数的单调减区间.
建湖县第二中学高二数学独立练习参考答案
时间:120分钟 2016.05.21
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.命题“,”的否定是 ▲ .
【知识点】命题的否定’
【答案解析】解析 :解:∵命题“,”是特称命题,∴否定命题为:.
故答案为:.
【思路点拨】由于命题是一个特称命题,故其否定是全称命题,根据特称命题的否定的格式即可.
2.设复数满足(为虚数单位),则的实部为 ▲ .
【知识点】复数代数形式的混合运算;复数的基本概念.
【答案解析】1解析 :解:由,得,
则的实部为1.
故答案为:1.
【思路点拨】由,两边除以,按照复数除法运算法则化简计算.
3.某校高一年级有400人,高二年级有600人,高三年级有500人,现要采取分层抽样的方法从全校学生中选出100名学生进行问卷调查,那么抽出的样本中高二年级的学生人数为 ▲ .
【知识点】分层抽样的方法.
【答案解析】40 解析 :解:设从高二学生中抽取的人数应为x,根据分层抽样的定义和方法可得,解得 x=40,
故答案为40.
【思路点拨】设从高二学生中抽取的人数应为x,根据分层抽样的定义和方法可得,由此求得x的值,即为所求.
4.“”是“”的 ▲ 条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个填空).
【知识点】必要条件、充分条件与充要条件的判断.
【答案解析】充分不必要解析 :解:由,得x>2或x<-2.即q:x>2或x<-2.∴是的充分不必要条件,
故答案为:充分不必要.
【思路点拨】求出成立的条件,根据充分条件和必要条件的定义进行判断.
5.一个盒子中放有大小相同的3个白球和1个黑球,从中任取两个球,则所取的两个球不同色的概率为 ▲ .
【知识点】古典概型及其概率计算公式.
【答案解析】解析 :解:∵总个数,
∵事件A中包含的基本事件的个数,∴p=
故答案为:.
【思路点拨】算出基本事件的总个数n=C42=6,再 算出事件A中包含的基本事件的个数m=C31=3,算出事件A的概率,即P(A)=即可.
6.根据如图所示的伪代码,可知输出的S的值为 ▲ .
【知识点】伪代码.
【答案解析】21解析 :解:由题意,第一次循环,i=3,S=2×3+3=9;第二次循环,i=5,S=2×5+3=13;第三次循环,i=7,S=2×7+3=17;第四次循环,i=9,S=2×9+3=21,退出循环
故答案为:21
【思路点拨】第一次循环,i=3,S=2×3+3=9;第二次循环,i=5,S=2×5+3=13;第三次循环,i=7,S=2×7+3=17;第四次循环,i=9,S=2×9+3=21,退出循环,故可得结论.
7.在平面直角坐标系中,已知中心在坐标原点的双曲线经过点,且它的右焦点与抛物线的焦点相同,则该双曲线的标准方程
为 ▲ .
【知识点】抛物线、双曲线方程.
【答案解析】解析 :解:抛物线的焦点坐标为(2,0),则双曲线的右焦点(2,0),所以,
设双曲线方程为代入点(1,0),可得,即,.
∴双曲线的方程为.
故答案为:.
【思路点拨】求出抛物线的焦点坐标,可得双曲线的一个顶点,设出双曲线方程,代入点的坐标,即可求出双曲线的方程.
8.已知点在不等式组所表示的平面区域内,则 的最大值为 ▲ .
【知识点】简单线性规划.
【答案解析】6解析:解:P(x,y)在不等式组表示的平面区域内,如图:
所以z=2x+y的经过A即的交点(2,2)时取得最大值:2×2+2=6.
故答案为:6.
【思路点拨】画出约束条件表示的可行域,确定目标函数经过的位置,求出最大值即可.
9.已知,,,….,类比这些等式,若(均为正实数),则= ▲ .
【知识点】类比推理.
【答案解析】41解析 :解:观察下列等式,,,….,第n个应该是=
则第5个等式中:a=6,b=a2-1=35,a+b=41.
故答案为:41.[]
【思路点拨】根据观察所给的等式,归纳出第n个式子,即可写出结果.
10.(理科学生做)已知展开式中所有项的二项式系数和为32,则其展开式中的常数项为 ▲ .
【知识点】二项式定理.[]
【答案解析】解析 :解:因为展开式中所有项的二项式系数和为:
,解得,由二项式展开式
整理得:,所以,故,则其展开式中的常数项为:.
故答案为:.
【思路点拨】先由所有项的二项式系数和求出,然后欲求展开式中的常数项,则令x的指数可求得结果.
(文科学生做)已知平面向量满足,,,则向量夹角的余弦值为 ▲ .
【知识点】数量积表示两个向量的夹角.
【答案解析】解析 :解:设向量的夹角为;因为,平方变形得:,解得:,所以.
故答案为:.
【思路点拨】先设出其夹角,根据已知条件整理出关于夹角的等式,解方程即可.
11.(理科学生做)现从8名学生中选出4人去参加一项活动,若甲、乙两名同学不能同时入选,则共有 ▲ 种不同的选派方案.(用数字作答)
【知识点】排列组合及简单计数问题.
【答案解析】55 解析 :解:从8名学生中选出4人,共有种选法,
其中甲乙同时参加的有种选法,
所以从8名学生中选出4人,甲乙不同时参加的选法有70-15=55种,
故答案为55.
【思路点拨】所有选法共有种,减去甲乙同时参加的情况种即可.
(文科学生做)设函数是奇函数,则实数的值为 ▲ .
【知识点】奇函数的定义.
【答案解析】解析 :解:因为函数,所以,
又因为函数是奇函数,所以,即,解得,
故答案为:.
【思路点拨】利用奇函数的定义解方程即可.
12.设正实数满足,则当取得最大值时,的值为 ▲ .[]
【知识点】基本不等式.
【答案解析】3解析 :解:因为为正实数,且,则,所以,当且仅当时等号成立,此时=3.
故答案为3.
【思路点拨】把原式整理代入并判断出等号成立的条件即可.
13.若函数在上单调递增,则实数的取值范围是 ▲ .
【知识点】函数的单调性;不等式恒成立问题.
【答案解析】解析 :解:因为在上单调递增,即
在上恒成立,令,即
在上恒成立,故,则.
故答案为:.
【思路点拨】先利用函数的单调性转化为不等式恒成立问题,然后求解即可.
14.设点为函数与图象的公共点,以为切点可作直线与两曲线都相切,则实数的最大值为 ▲ .
【知识点】导数的几何意义;利用导数求最大值.
【答案解析】解析 :解:设点坐标为,则有,因为以为切点可作直线与两曲线都相切,所以,即
或由,故,此时;所以点坐标为,代入整理得:,,令,即,得,可判断当时有极大值也是最大值,,
故答案为:.
【思路点拨】设点坐标为满足两个函数解析式成立,再借助于斜率相同可解得a,代入函数,最后利用导数求最大值即可.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.[]
15.(本小题满分14分)
(理科学生做)设某地区型血的人数占总人口数的比为,现从中随机抽取3人.
(1)求3人中恰有2人为型血的概率;
(2)记型血的人数为,求的概率分布与数学期望.
【知识点】n次独立重复试验恰有k次发生的概率;分布列;期望.
【答案解析】(1)(2)
解析 :解:(1)由题意,随机抽取一人,是型血的概率为, …………2分
3人中有2人为型血的概率为. …………6分
(2)的可能取值为0,1,2,3, …………8分
, , ,
, …………12分
. …………14分
【思路点拨】(1)代入n次独立重复试验恰有k次发生的概率的公式即可;(2)根据n次独立重复试验恰有k次发生的概率的公式依次求出为0,1,2,3,时的概率,最后求出期望值.[]
(文科学生做)给定两个命题,:对任意实数都有恒成立;:.如果为真命题,为假命题,求实数的取值范围.
试题解析:解:命题:ax2+ax+1>0恒成立
当a=0时,不等式恒成立,满足题意)
当a≠0时,,解得0<a<4
∴0≤a<4
命题:a2+8a﹣20<0解得﹣10<a<2
∵为真命题,为假命题∴有且只有一个为真,
当真假时得
当假真时得
所以﹣10<a<0或2≤a<4
16.(本小题满分14分)
(理科学生做)设数列满足,.
(1)求;
(2)先猜想出的一个通项公式,再用数学归纳法证明你的猜想.
【知识点】数学归纳法;归纳推理.
【答案解析】(1)(2),证明见解析.
解析 :解:(1)由条件,依次得,
,, …………6分
(2)由(1),猜想. …………7分
下用数学归纳法证明之:
①当时,,猜想成立; ………8分
②假设当时,猜想成立,即有, …………9分
则当时,有,
即当时猜想也成立, …………13分
综合①②知,数列通项公式为. …………14分
【思路点拨】(1)直接利用已知关系式,通过n=1,2,3,4,求出a2,a3,a4;
(2)利用(1)猜想数列的通项公式,利用数学归纳法证明的步骤证明即可.(文科学生做)已知函数()的一段图象如图所示.
(1)求函数的解析式;
(2)求函数的单调增区间;
(3)若,求函数的值域.
(1)由题意知:,∴,
又,∴,
,又,∴.
∴函数的解析式:.
(2)由,,得,
所以的增区间为,,
(3)∵,∴,
∴.
∴值域为
17.(本小题满分14分)
(理科学生做)如图,在直三棱柱中,,分别是的中点,且.
(1)求直线与所成角的大小;
(2)求直线与平面所成角的正弦值.
【知识点】异面直线所成的角;直线与平面所成的角.
【答案解析】(1)(2)
解析 :解:分别以、、所在直线为轴建立空间直角坐标系.
则由题意可得:,,,,,,
又分别是的中点,,. …………3分
(1)因为, ,
所以, …………7分
直线与所成角的大小为. …………8分
(2)设平面的一个法向量为,由,得,
可取, …………10分
又,所以, ……13分
直线与平面所成角的正弦值为. …………14分
【思路点拨】(1)分别以、、所在直线为轴建立空间直角坐标系.
则由题意可得, ,然后利用向量的夹角公式计算可得结果;(2)找出两个半平面的法向量后利用向量的夹角公式计算即可.
(文科学生做)设函数.
(1)用反证法证明:函数不可能为偶函数;
(2)求证:函数在上单调递减的充要条件是.
【知识点】反证法与放缩法;必要条件、充分条件与充要条件的判断.
【答案解析】(1)见解析(2)见解析
解析 :解:(1)假设函数是偶函数, …………2分
则,即,解得, …………4分
这与矛盾,所以函数不可能是偶函数. …………6分
(2)因为,所以. …………8分
①充分性:当时,,
所以函数在单调递减; …………10分
②必要性:当函数在单调递减时,
有,即,又,所以. …………13分
综合①②知,原命题成立. …………14分
【思路点拨】(1)假设函数f(x)为偶函数,则f(-x)=f(x),代入利用对数的性质,可得矛盾,即可得证;
(2)分充分性、必要性进行论证,即可得到结论.
18.(本小题满分16分)
如图所示,某人想制造一个支架,它由四根金属杆构成,其底端三点均匀地固定在半径为的圆上(圆在地面上),三点相异且共线,与地面垂直. 现要求点到地面的距离恰为,记用料总长为,设.
(1)试将表示为的函数,并注明定义域;
(2)当的正弦值是多少时,用料最省?
【知识点】函数解析式与定义域的求法;利用导数求函数的最知.
【答案解析】(1),.
(2)时用料最省.
解析 :解:(1)因与地面垂直,且,
则是
全等的直角三角形,又圆的半径为3,
所以,, …………3分
又,所以, …………6分
若点重合,则,即,所以,
从而,. …………7分
(2)由(1)知,
所以,当时,, …………11分
令,,当时,;当时,;
所以函数L在上单调递减,在上单调递增, …………15分
所以当,即时,L有最小值,此时用料最省. …………16分
【思路点拨】(1)通过图形分别求出的值,然后写出解析式并注明定义域即可;(2)利用导数结合单调性即可求出最值.
19.(本小题满分16分)
如图所示,在平面直角坐标系中,设椭圆,其中,过椭圆内一点的两条直线分别与椭圆交于点和,且满足,,其中为正常数. 当点恰为椭圆的右顶点时,对应的.
(1)求椭圆的离心率;
(2)求与的值;
(3)当变化时,是否为定值?若是,请求出此定值;
若不是,请说明理由.
【知识点】椭圆的性质;椭圆的标准方程;根与系数的关系.
【答案解析】(1)(2)(3)为定值.
解析 :解:(1)因为,所以,得,即,
所以离心率. ………4分
(2)因为,,所以由,得, ………7分
将它代入到椭圆方程中,得,解得,
所以. ………10分
(3)法一:设,
由,得, ………12分
又椭圆的方程为,所以由,
得 ①, 且 ②,
由②得,,
即,
结合①,得, ………14分
同理,有,所以,
从而,即为定值. ………16分[]
法二:设,
由,得,同理,……12分
将坐标代入椭圆方程得,两式相减得
,
即, ……14分
同理,,
而,所以,
所以,
所以,
即,所以为定值. ………16分
【思路点拨】(1)根据椭圆的性质求出a,c的关系式即可;(2)由得代入到椭圆方程中即可得结果;
(3)设,由,得到点坐标间的关系,再将将坐标代入椭圆方程后两式相减,再利用即可.
20.(本小题满分16分)
设函数.
(1)当时,求函数的极大值;
(2)若函数的图象与函数的图象有三个不同的交点,求的取值范围;
(3)设,当时,求函数的单调减区间.
【知识点】利用导数求极值;借助导数求范围;利用导数求单调区间.
【答案解析】(1)极大值为5.(2);
(3)①当时,函数的单调减区间为;②当时,函数的单调减区间为,;
③当时,函数的单调减区间为,, .
解析 :解:(1)当时,由=0,得或, ………2分
列表如下:
-1 3
+ 0 - 0 +
递增 极大 递减 极小 递增
所以当时,函数取得极大值为5. ………4分
(2)由,得,即, ………6分
令,则,
列表,得
1
- 0 + 0 -
递减 极小值 递增 极大值2 递减
………8分
由题意知,方程有三个不同的根,故的取值范围是. ………10分
(3)因为,
所以当时,在R上单调递增;
当时,的两根为,且,
所以此时在上递增,在上递减,在上递增; ………12分
令,得,或 (),
当时,方程()无实根或有相等实根;当时,方程()有两根,
………13分
从而
①当时,函数的单调减区间为; ………14分
②当时,函数的单调减区间为,; ……15分
③当时,函数的单调减区间为,, . ………16分
【思路点拨】(1)当时,求出原函数的导数,找到极值点列表求出极大值;(2)原式变型为,令,然后通过列表找到a的取值范围;(3)对a进行分类讨论即可.
第6题
A
B
C
A1
B1
C1
E
D
第17题
O
P
H
A
B
C
θ
第18题
O
A
B
P
C
D
x
y
第19题
第6题
A
B
C
A1
B1
C1
E
D
第17题
O
P
H
A
B
C
θ
第18题
O
A
B
P
C
D
x
y
第19题
时间:120分钟
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.命题“,”的否定是 ▲ .
2.设复数满足(为虚数单位),则的实部为 ▲ .
3.某校高一年级有400人,高二年级有600人,高三年级有500人,现要采取分层抽样的方法从全校学生中选出100名学生进行问卷调查,那么抽出的样本中高二年级的学生人数为 ▲ .
4.“”是“”的 ▲ 条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个填空).
5.一个盒子中放有大小相同的3个白球和1个黑球,从中任取两个球,则所取的两个球不同色的概率为 ▲ .
6.根据如图所示的伪代码,可知输出的S的值为 ▲ .
7.在平面直角坐标系中,已知中心在坐标原点的双曲线经过点,且它的右焦点与抛物线的焦点相同,则该双曲线的标准方程
为 ▲ .
8.已知点在不等式组所表示
的平面区域内,则 的最大值为 ▲ .
9.已知,,,….,
类比这些等式,若(均为正实数),则= ▲ .
10.(理科学生做)已知展开式中所有项的二项式系数和为32,则其展开式中的常数项为 ▲ .
(文科学生做)已知平面向量满足,,,则向量夹角的余弦值为 ▲ .
11.(理科学生做)现从8名学生中选出4人去参加一项活动,若甲、乙两名同学不能同时入选,则共有 ▲ 种不同的选派方案.(用数字作答)
(文科学生做)设函数是奇函数,则实数的值为 ▲ .
12.设正实数满足,则当取得最大值时,的值为
▲ .
13.若函数在上单调递增,则实数的取值范围是 ▲ .
14.设点为函数与图象的公共点,以为切点可作直线与两曲线都相切,则实数的最大值为 ▲ .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
(理科学生做)设某地区型血的人数占总人口数的比为,现从中随机抽取3人.
(1)求3人中恰有2人为型血的概率;
(2)记型血的人数为,求的概率分布与数学期望.
(文科学生做)给定两个命题,:对任意实数都有恒成立;:.如果为真命题,为假命题,求实数的取值范围.
16.(本小题满分14分)
(理科学生做)设数列满足,.
(1)求;
(2)先猜想出的一个通项公式,再用数学归纳法证明你的猜想.
(文科学生做)已知函数()的一段图象如图所示.
(1)求函数的解析式;
(2)求函数的单调增区间;
(3)若,求函数的值域.
17.(本小题满分14分)
(理科学生做)如图,在直三棱柱中,,分别是的中点,且.
(1)求直线与所成角的大小;
(2)求直线与平面所成角的正弦值.
(文科学生做)设函数.
(1)用反证法证明:函数不可能为偶函数;
(2)求证:函数在上单调递减的充要条件是.
18.(本小题满分16分)
如图所示,某人想制造一个支架,它由四根金属杆构成,其底端三点均匀地固定在半径为的圆上(圆在地面上),三点相异且共线,与地面垂直. 现要求点到地面的距离恰为,记用料总长为,设.
(1)试将表示为的函数,并注明定义域;
(2)当的正弦值是多少时,用料最省?
19.(本小题满分16分)
如图所示,在平面直角坐标系中,设椭圆,其中,过椭圆内一点的两条直线分别与椭圆交于点和,且满足,,其中为正常数. 当点恰为椭圆的右顶点时,对应的.
(1)求椭圆的离心率;
(2)求与的值;
(3)当变化时,是否为定值?若是,请求出此定值;
若不是,请说明理由.
20.(本小题满分16分)
设函数.
(1)当时,求函数的极大值;
(2)若函数的图象与函数的图象有三个不同的交点,求的取值范围;
(3)设,当时,求函数的单调减区间.
建湖县第二中学高二数学独立练习参考答案
时间:120分钟 2016.05.21
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.命题“,”的否定是 ▲ .
【知识点】命题的否定’
【答案解析】解析 :解:∵命题“,”是特称命题,∴否定命题为:.
故答案为:.
【思路点拨】由于命题是一个特称命题,故其否定是全称命题,根据特称命题的否定的格式即可.
2.设复数满足(为虚数单位),则的实部为 ▲ .
【知识点】复数代数形式的混合运算;复数的基本概念.
【答案解析】1解析 :解:由,得,
则的实部为1.
故答案为:1.
【思路点拨】由,两边除以,按照复数除法运算法则化简计算.
3.某校高一年级有400人,高二年级有600人,高三年级有500人,现要采取分层抽样的方法从全校学生中选出100名学生进行问卷调查,那么抽出的样本中高二年级的学生人数为 ▲ .
【知识点】分层抽样的方法.
【答案解析】40 解析 :解:设从高二学生中抽取的人数应为x,根据分层抽样的定义和方法可得,解得 x=40,
故答案为40.
【思路点拨】设从高二学生中抽取的人数应为x,根据分层抽样的定义和方法可得,由此求得x的值,即为所求.
4.“”是“”的 ▲ 条件(在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选择一个填空).
【知识点】必要条件、充分条件与充要条件的判断.
【答案解析】充分不必要解析 :解:由,得x>2或x<-2.即q:x>2或x<-2.∴是的充分不必要条件,
故答案为:充分不必要.
【思路点拨】求出成立的条件,根据充分条件和必要条件的定义进行判断.
5.一个盒子中放有大小相同的3个白球和1个黑球,从中任取两个球,则所取的两个球不同色的概率为 ▲ .
【知识点】古典概型及其概率计算公式.
【答案解析】解析 :解:∵总个数,
∵事件A中包含的基本事件的个数,∴p=
故答案为:.
【思路点拨】算出基本事件的总个数n=C42=6,再 算出事件A中包含的基本事件的个数m=C31=3,算出事件A的概率,即P(A)=即可.
6.根据如图所示的伪代码,可知输出的S的值为 ▲ .
【知识点】伪代码.
【答案解析】21解析 :解:由题意,第一次循环,i=3,S=2×3+3=9;第二次循环,i=5,S=2×5+3=13;第三次循环,i=7,S=2×7+3=17;第四次循环,i=9,S=2×9+3=21,退出循环
故答案为:21
【思路点拨】第一次循环,i=3,S=2×3+3=9;第二次循环,i=5,S=2×5+3=13;第三次循环,i=7,S=2×7+3=17;第四次循环,i=9,S=2×9+3=21,退出循环,故可得结论.
7.在平面直角坐标系中,已知中心在坐标原点的双曲线经过点,且它的右焦点与抛物线的焦点相同,则该双曲线的标准方程
为 ▲ .
【知识点】抛物线、双曲线方程.
【答案解析】解析 :解:抛物线的焦点坐标为(2,0),则双曲线的右焦点(2,0),所以,
设双曲线方程为代入点(1,0),可得,即,.
∴双曲线的方程为.
故答案为:.
【思路点拨】求出抛物线的焦点坐标,可得双曲线的一个顶点,设出双曲线方程,代入点的坐标,即可求出双曲线的方程.
8.已知点在不等式组所表示的平面区域内,则 的最大值为 ▲ .
【知识点】简单线性规划.
【答案解析】6解析:解:P(x,y)在不等式组表示的平面区域内,如图:
所以z=2x+y的经过A即的交点(2,2)时取得最大值:2×2+2=6.
故答案为:6.
【思路点拨】画出约束条件表示的可行域,确定目标函数经过的位置,求出最大值即可.
9.已知,,,….,类比这些等式,若(均为正实数),则= ▲ .
【知识点】类比推理.
【答案解析】41解析 :解:观察下列等式,,,….,第n个应该是=
则第5个等式中:a=6,b=a2-1=35,a+b=41.
故答案为:41.[]
【思路点拨】根据观察所给的等式,归纳出第n个式子,即可写出结果.
10.(理科学生做)已知展开式中所有项的二项式系数和为32,则其展开式中的常数项为 ▲ .
【知识点】二项式定理.[]
【答案解析】解析 :解:因为展开式中所有项的二项式系数和为:
,解得,由二项式展开式
整理得:,所以,故,则其展开式中的常数项为:.
故答案为:.
【思路点拨】先由所有项的二项式系数和求出,然后欲求展开式中的常数项,则令x的指数可求得结果.
(文科学生做)已知平面向量满足,,,则向量夹角的余弦值为 ▲ .
【知识点】数量积表示两个向量的夹角.
【答案解析】解析 :解:设向量的夹角为;因为,平方变形得:,解得:,所以.
故答案为:.
【思路点拨】先设出其夹角,根据已知条件整理出关于夹角的等式,解方程即可.
11.(理科学生做)现从8名学生中选出4人去参加一项活动,若甲、乙两名同学不能同时入选,则共有 ▲ 种不同的选派方案.(用数字作答)
【知识点】排列组合及简单计数问题.
【答案解析】55 解析 :解:从8名学生中选出4人,共有种选法,
其中甲乙同时参加的有种选法,
所以从8名学生中选出4人,甲乙不同时参加的选法有70-15=55种,
故答案为55.
【思路点拨】所有选法共有种,减去甲乙同时参加的情况种即可.
(文科学生做)设函数是奇函数,则实数的值为 ▲ .
【知识点】奇函数的定义.
【答案解析】解析 :解:因为函数,所以,
又因为函数是奇函数,所以,即,解得,
故答案为:.
【思路点拨】利用奇函数的定义解方程即可.
12.设正实数满足,则当取得最大值时,的值为 ▲ .[]
【知识点】基本不等式.
【答案解析】3解析 :解:因为为正实数,且,则,所以,当且仅当时等号成立,此时=3.
故答案为3.
【思路点拨】把原式整理代入并判断出等号成立的条件即可.
13.若函数在上单调递增,则实数的取值范围是 ▲ .
【知识点】函数的单调性;不等式恒成立问题.
【答案解析】解析 :解:因为在上单调递增,即
在上恒成立,令,即
在上恒成立,故,则.
故答案为:.
【思路点拨】先利用函数的单调性转化为不等式恒成立问题,然后求解即可.
14.设点为函数与图象的公共点,以为切点可作直线与两曲线都相切,则实数的最大值为 ▲ .
【知识点】导数的几何意义;利用导数求最大值.
【答案解析】解析 :解:设点坐标为,则有,因为以为切点可作直线与两曲线都相切,所以,即
或由,故,此时;所以点坐标为,代入整理得:,,令,即,得,可判断当时有极大值也是最大值,,
故答案为:.
【思路点拨】设点坐标为满足两个函数解析式成立,再借助于斜率相同可解得a,代入函数,最后利用导数求最大值即可.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.[]
15.(本小题满分14分)
(理科学生做)设某地区型血的人数占总人口数的比为,现从中随机抽取3人.
(1)求3人中恰有2人为型血的概率;
(2)记型血的人数为,求的概率分布与数学期望.
【知识点】n次独立重复试验恰有k次发生的概率;分布列;期望.
【答案解析】(1)(2)
解析 :解:(1)由题意,随机抽取一人,是型血的概率为, …………2分
3人中有2人为型血的概率为. …………6分
(2)的可能取值为0,1,2,3, …………8分
, , ,
, …………12分
. …………14分
【思路点拨】(1)代入n次独立重复试验恰有k次发生的概率的公式即可;(2)根据n次独立重复试验恰有k次发生的概率的公式依次求出为0,1,2,3,时的概率,最后求出期望值.[]
(文科学生做)给定两个命题,:对任意实数都有恒成立;:.如果为真命题,为假命题,求实数的取值范围.
试题解析:解:命题:ax2+ax+1>0恒成立
当a=0时,不等式恒成立,满足题意)
当a≠0时,,解得0<a<4
∴0≤a<4
命题:a2+8a﹣20<0解得﹣10<a<2
∵为真命题,为假命题∴有且只有一个为真,
当真假时得
当假真时得
所以﹣10<a<0或2≤a<4
16.(本小题满分14分)
(理科学生做)设数列满足,.
(1)求;
(2)先猜想出的一个通项公式,再用数学归纳法证明你的猜想.
【知识点】数学归纳法;归纳推理.
【答案解析】(1)(2),证明见解析.
解析 :解:(1)由条件,依次得,
,, …………6分
(2)由(1),猜想. …………7分
下用数学归纳法证明之:
①当时,,猜想成立; ………8分
②假设当时,猜想成立,即有, …………9分
则当时,有,
即当时猜想也成立, …………13分
综合①②知,数列通项公式为. …………14分
【思路点拨】(1)直接利用已知关系式,通过n=1,2,3,4,求出a2,a3,a4;
(2)利用(1)猜想数列的通项公式,利用数学归纳法证明的步骤证明即可.(文科学生做)已知函数()的一段图象如图所示.
(1)求函数的解析式;
(2)求函数的单调增区间;
(3)若,求函数的值域.
(1)由题意知:,∴,
又,∴,
,又,∴.
∴函数的解析式:.
(2)由,,得,
所以的增区间为,,
(3)∵,∴,
∴.
∴值域为
17.(本小题满分14分)
(理科学生做)如图,在直三棱柱中,,分别是的中点,且.
(1)求直线与所成角的大小;
(2)求直线与平面所成角的正弦值.
【知识点】异面直线所成的角;直线与平面所成的角.
【答案解析】(1)(2)
解析 :解:分别以、、所在直线为轴建立空间直角坐标系.
则由题意可得:,,,,,,
又分别是的中点,,. …………3分
(1)因为, ,
所以, …………7分
直线与所成角的大小为. …………8分
(2)设平面的一个法向量为,由,得,
可取, …………10分
又,所以, ……13分
直线与平面所成角的正弦值为. …………14分
【思路点拨】(1)分别以、、所在直线为轴建立空间直角坐标系.
则由题意可得, ,然后利用向量的夹角公式计算可得结果;(2)找出两个半平面的法向量后利用向量的夹角公式计算即可.
(文科学生做)设函数.
(1)用反证法证明:函数不可能为偶函数;
(2)求证:函数在上单调递减的充要条件是.
【知识点】反证法与放缩法;必要条件、充分条件与充要条件的判断.
【答案解析】(1)见解析(2)见解析
解析 :解:(1)假设函数是偶函数, …………2分
则,即,解得, …………4分
这与矛盾,所以函数不可能是偶函数. …………6分
(2)因为,所以. …………8分
①充分性:当时,,
所以函数在单调递减; …………10分
②必要性:当函数在单调递减时,
有,即,又,所以. …………13分
综合①②知,原命题成立. …………14分
【思路点拨】(1)假设函数f(x)为偶函数,则f(-x)=f(x),代入利用对数的性质,可得矛盾,即可得证;
(2)分充分性、必要性进行论证,即可得到结论.
18.(本小题满分16分)
如图所示,某人想制造一个支架,它由四根金属杆构成,其底端三点均匀地固定在半径为的圆上(圆在地面上),三点相异且共线,与地面垂直. 现要求点到地面的距离恰为,记用料总长为,设.
(1)试将表示为的函数,并注明定义域;
(2)当的正弦值是多少时,用料最省?
【知识点】函数解析式与定义域的求法;利用导数求函数的最知.
【答案解析】(1),.
(2)时用料最省.
解析 :解:(1)因与地面垂直,且,
则是
全等的直角三角形,又圆的半径为3,
所以,, …………3分
又,所以, …………6分
若点重合,则,即,所以,
从而,. …………7分
(2)由(1)知,
所以,当时,, …………11分
令,,当时,;当时,;
所以函数L在上单调递减,在上单调递增, …………15分
所以当,即时,L有最小值,此时用料最省. …………16分
【思路点拨】(1)通过图形分别求出的值,然后写出解析式并注明定义域即可;(2)利用导数结合单调性即可求出最值.
19.(本小题满分16分)
如图所示,在平面直角坐标系中,设椭圆,其中,过椭圆内一点的两条直线分别与椭圆交于点和,且满足,,其中为正常数. 当点恰为椭圆的右顶点时,对应的.
(1)求椭圆的离心率;
(2)求与的值;
(3)当变化时,是否为定值?若是,请求出此定值;
若不是,请说明理由.
【知识点】椭圆的性质;椭圆的标准方程;根与系数的关系.
【答案解析】(1)(2)(3)为定值.
解析 :解:(1)因为,所以,得,即,
所以离心率. ………4分
(2)因为,,所以由,得, ………7分
将它代入到椭圆方程中,得,解得,
所以. ………10分
(3)法一:设,
由,得, ………12分
又椭圆的方程为,所以由,
得 ①, 且 ②,
由②得,,
即,
结合①,得, ………14分
同理,有,所以,
从而,即为定值. ………16分[]
法二:设,
由,得,同理,……12分
将坐标代入椭圆方程得,两式相减得
,
即, ……14分
同理,,
而,所以,
所以,
所以,
即,所以为定值. ………16分
【思路点拨】(1)根据椭圆的性质求出a,c的关系式即可;(2)由得代入到椭圆方程中即可得结果;
(3)设,由,得到点坐标间的关系,再将将坐标代入椭圆方程后两式相减,再利用即可.
20.(本小题满分16分)
设函数.
(1)当时,求函数的极大值;
(2)若函数的图象与函数的图象有三个不同的交点,求的取值范围;
(3)设,当时,求函数的单调减区间.
【知识点】利用导数求极值;借助导数求范围;利用导数求单调区间.
【答案解析】(1)极大值为5.(2);
(3)①当时,函数的单调减区间为;②当时,函数的单调减区间为,;
③当时,函数的单调减区间为,, .
解析 :解:(1)当时,由=0,得或, ………2分
列表如下:
-1 3
+ 0 - 0 +
递增 极大 递减 极小 递增
所以当时,函数取得极大值为5. ………4分
(2)由,得,即, ………6分
令,则,
列表,得
1
- 0 + 0 -
递减 极小值 递增 极大值2 递减
………8分
由题意知,方程有三个不同的根,故的取值范围是. ………10分
(3)因为,
所以当时,在R上单调递增;
当时,的两根为,且,
所以此时在上递增,在上递减,在上递增; ………12分
令,得,或 (),
当时,方程()无实根或有相等实根;当时,方程()有两根,
………13分
从而
①当时,函数的单调减区间为; ………14分
②当时,函数的单调减区间为,; ……15分
③当时,函数的单调减区间为,, . ………16分
【思路点拨】(1)当时,求出原函数的导数,找到极值点列表求出极大值;(2)原式变型为,令,然后通过列表找到a的取值范围;(3)对a进行分类讨论即可.
第6题
A
B
C
A1
B1
C1
E
D
第17题
O
P
H
A
B
C
θ
第18题
O
A
B
P
C
D
x
y
第19题
第6题
A
B
C
A1
B1
C1
E
D
第17题
O
P
H
A
B
C
θ
第18题
O
A
B
P
C
D
x
y
第19题
同课章节目录
