江苏省苏州市2024-2025学年高一(下)期中物理试卷(含解析)
文档属性
| 名称 | 江苏省苏州市2024-2025学年高一(下)期中物理试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 748.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-23 08:54:52 | ||
图片预览




文档简介
江苏省苏州市2024-2025学年高一(下)期中物理试卷
一、单选题:本大题共10小题,共40分。
1.开普勒用年时间研究了丹麦一位天文学家的行星观测记录,最终发表了著名的开普勒三定律,这位天文学家是( )
A. 伽利略 B. 第谷 C. 托勒密 D. 哥白尼
2.下列选项中所运用的主要研究方法与卡文迪什测量引力常量的主要研究方法相同的是( )
A. 图甲中,通过平面镜的反射光线观察桌面的微小形变
B. 图乙中,利用作用效果相同研究合力与分力的关系
C. 图丙中,通过物体沿曲面运动研究重力做功的特点
D. 图丁中,利用该装置研究力与运动的关系
3.年月日,航天员王亚平再次进行太空授课,展示了一个奇妙现象:浸在水中的乒乓球因浮力消失而不会浮出水面下列说法正确的是( )
A. 水处于完全失重状态
B. 乒乓球不受任何力的作用
C. 乒乓球所受的合力为零
D. 在空间站若将装满水的杯子转动至杯口朝下,水会自动流出
4.旋转飞椅可简化成如图所示模型长为的钢绳一端系有质量为可视为质点的小球,另一端固定在直径为的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动当转盘匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向夹角为,不计钢绳的重力,此时钢绳的拉力为下列说法正确的是( )
A. 小球做圆周运动的半径为 B. 小球做圆周运动的轨迹圆心为点
C. 钢绳拉力的大小与向心力大小相等 D. 钢绳拉力沿水平方向的分力提供向心力
5.据报道,“天问一号”火星探测器以及“祝融号”火星车在年月份失联了一个月,失联的原因是由于太阳处在地球与火星中间,出现严重的“日凌干扰”现象,情景如图所示。已知地球、火星均沿轨道逆时针运动,地球公转周期为年,火星公转周期为年,试估算下次“日凌干扰”大约出现在
A. 年月 B. 年月 C. 年月 D. 年月
6.年月,“空中出租车”在上海试飞成功,完成首秀。质量为的“空中出租车”在竖直方向的牵引力作用下,从静止开始竖直上升,其运动图像如图所示,为匀加速阶段,时刻“空中出租车”达到功率并保持不变,运动过程中阻力大小恒定。下列说法正确的是( )
A. 整个过程牵引力保持不变 B. 过程,牵引力做功为
C. 阻力大小为 D. 时刻“空中出租车”的功率为
7.据报道,“恒星系统”由颗红矮星和颗如图所示围绕它运行的行星组成,若地球半径为,则行星的半径如下表。据推测行星和的密度大致相同,若行星的第一宇宙速度为,则行星的第一宇宙速度约为( )
行星
半径
A. B. C. D.
8.某种变速自行车有六个飞轮和三个链轮,链轮和飞轮的齿数如下表,前后轮直径为,人骑该车行进速度为,脚踩踏板做匀速圆周运动的最大角速度约为( )
名称 链轮 飞轮
齿数个
A. B. C. D.
9.竖直细圆杆顶端附近有一小孔,光滑细绳穿过小孔,细绳两端分别系有、两小球,已知球质量小于球质量。调节细绳并转动圆杆,使得两球与圆杆能以相同角速度在水平面内匀速转动,下列图样大致正确的是( )
A. B. C. D.
10.如图所示,质量为的小球从与轻弹簧上端相距处静止释放,弹簧的劲度系数为,重力加速度为,不计一切阻力,则小球在向下运动的过程中( )
A. 最大加速度为
B. 最大加速度小于
C. 最大速度为
D. 最大速度为
二、实验题:本大题共1小题,共15分。
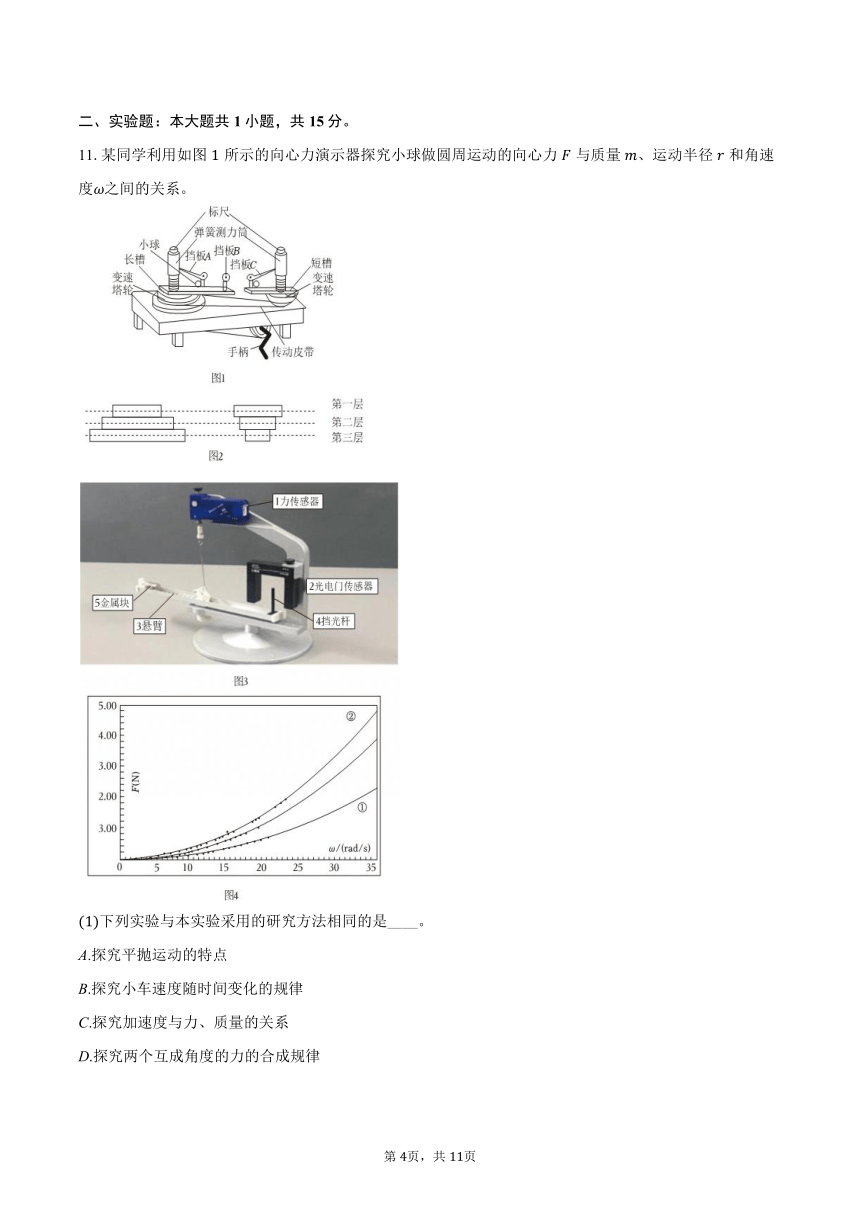
11.某同学利用如图所示的向心力演示器探究小球做圆周运动的向心力与质量、运动半径和角速度之间的关系。
下列实验与本实验采用的研究方法相同的是____。
A.探究平抛运动的特点
B.探究小车速度随时间变化的规律
C.探究加速度与力、质量的关系
D.探究两个互成角度的力的合成规律
探究向心力和质量的关系时,将传动皮带套在半径相同的两塔轮轮盘上,应将质量不同的小球分别放在挡板_______处选填“和”、“和”、“和”。
实验中若将传动皮带套在半径不同的两塔轮轮盘上,是为了探究向心力大小与_______选填“角速度”、“半径”、“质量”的关系。
器材说明书上说第二层塔轮半径之比为:,如图所示在进行实验探究前,如果仅使用向心力演示仪来验证这个半径关系,你打算怎么做?___________________。
某兴趣小组用如图所示的传感器装置定量验证向心力的表达式。图中两条曲线为相同半径、不同质量下向心力与角速度的关系图线,可知曲线对应的金属块质量______选填“大于”、“小于”、“等于”曲线对应的金属块质量。
三、计算题:本大题共4小题,共45分。
12.随着航天科技的飞速发展,我国向火星发射多枚探测器。如图所示,假设质量为的某一探测器绕火星做匀速圆周运动。已知火星的质量为,半径为,探测器距离火星表面的高度也等于,万有引力常量为。求:
探测器受到火星的万有引力大小;
探测器的运行速度大小。
13.如图所示,飞轮半径为,质量为,为竖直转动轴。正常工作时转动轴受到的水平作用力可以认为是。如果高速转动的飞轮的重心不在转轴上,运行将不稳定,而且轴承会受到很大的作用力,加速磨损。假想在飞轮的边缘固定一个质量的小螺丝钉,此时飞轮转速为单位为。求:
螺丝钉的线速度大小;
转动轴受到的水平作用力的大小。
14.如图所示为某弹射装置的示意图。半径为的光滑半圆形轨道竖直固定放置,轨道最高点处有一弹射装置,轨道下端与水平轨道相切,水平轨道左侧处有一固定挡板未知且不为零。可视为质点的物块被弹簧弹射后从处进入半圆形轨道,恰好能够沿半圆轨道运动,进入水平轨道后与挡板发生弹性碰撞碰撞前后速度大小不变。已知物块的质量为,物块与水平轨道间的动摩擦因数为,重力加速度为。求:
初始时刻弹簧的弹性势能;
物块第一次到达圆轨道下端时对轨道的压力;
若物块被挡板反弹后不脱离轨道,则应满足什么条件。
15.如图所示,长为,质量为且质量分布均匀的软绳,放在长为的斜面上,斜面顶端有一个很小的固定滑轮,斜面倾角,软绳一端刚好接触滑轮,并通过一根轻绳跨过滑轮系着一物块,软绳恰好不下滑。忽略空气阻力,不计两绳与滑轮之间的摩擦,重力加速度为,软绳与斜面之间的动摩擦因数为,最大静摩擦力等于滑动摩擦力。
求物块的质量;
若物块的质量为,软绳从静止开始下滑,物块始终没有触碰到滑轮,求软绳下端滑至斜面底端时的速度大小;
若物块的质量为,软绳与滑轮平滑连接,在软绳从静止开始到全部滑出滑轮的过程中物块始终没有落地,求轻绳对物块做的功。
答案和解析
1.【答案】
【解析】解:开普勒仔细研究了丹麦天文学家第谷连续年对行星的观测结果,最终发表了著名的开普勒三定律。故ACD错误,B正确。
故选:。
2.【答案】
【解析】卡文迪什扭秤实验运用了放大的思想方法。图甲中,借助激光器及平面镜观察桌面微小形变运用了放大法;
图乙中,应用等效替代的实验方法;
图丙中,运用微元法的物理思想;
图丁中运用实验和逻辑推理相结合的方法,故A正确,BCD错误。
故选:。
3.【答案】
【解析】A.空间站中的物体都处于完全失重状态,水处于完全失重状态,故A正确;
乒乓球仍然受到地球引力的作用,由万有引力提供向心力,合力不为零,故BC错误;
D.由于空间站的物体处于完全失重状态,其万有引力用来提供向心力,装满水的杯子杯口朝下,水也不会流出,故D错误。
4.【答案】
【解析】小球以小球与转轴垂线交点为圆心做圆周运动,轨道半径为,故AB错误;
钢绳拉力的竖直方向分力与重力平衡,水平分力提供向心力,故C错误,D正确。
5.【答案】
【解析】设两次日凌干扰的时间间隔为,则有,已知年,年,
解得解得:年年,所以下次“日凌干扰”大约出现在年月,故ABD错误,故C正确。
6.【答案】
【解析】A.根据题意可知,匀加速过程牵引力保持不变,功率达到后牵引力逐渐减小,最后保持不变,故A错误;
B.过程,匀加速阶段功率小于,则整个过程中牵引力做功小于,故B错误;
当速度达到最大速度时,根据平衡条件有,
则阻力大小,
故C错误;
根据图像可知时刻“空中出租车”的速度为,
牵引力,
则该时刻的功率为 ,
故D正确。
故选:。
7.【答案】
【解析】行星的第一宇宙速度为,则有
可得第一宇宙速度
同理行星的第一宇宙速度为
,故B正确。
8.【答案】
【解析】当自行车行驶速度一定时,即后轮的角速度一定,飞轮的角速度一定,根据,由于脚踏板和链轮有相同的角速度,当脚踏板做匀速圆周运动的角速度最大时, 最少, 最多,即,,再由,可得。
故选B。
9.【答案】
【解析】两个小球均做匀速圆周运动,设其中一个小球悬线长为,悬线与杆的夹角为,小球的质量为,做匀速圆周运动的角速度为,受力情况如图所示:
根据牛顿第二定律可得:,解得:,由于相同,则相等,即悬线在竖直方向的分量相等,两个小球的轨迹平面在同一水平面内,故B正确、ACD错误。
故选:。
10.【答案】
【解析】、小球与弹簧相互作用时,牛顿第二定律,得,作出图像,围成面积的含义为,加速度减为零时,轴坐标为,速度最大,根据图像在第一象限围成面积,此时最大速度为,故D正确,C错误;
、小球最后速度为零,图像在第一象限围成面积与在第四象限围成面积相等,可得最大加速度大于,故AB错误。
11.【答案】;和;角速度;控制小球的质量与圆周运动的半径相同,测量出向心力的大小关系,由,得到角速度的关系,在根据,验证塔轮半径的关系;小于
【解析】本实验采用的研究方法是控制变量法,四个选项只有探究加速度与力、质量的关系的实验采用的是控制变量法,故C正确,ABD错误。
故选:。
探究向心力和质量的关系时,将传动皮带套在半径相同的两塔轮轮盘上,是控制角速度相同,还应控制小球做圆周运动的半径相同,故应将质量不同的小球分别放在挡板的和处。
若将传动皮带套在半径不同的两塔轮轮盘上,则小球的角速度不同,故是为了探究向心力大小与角速度的关系。
用向心力演示仪来验证这个塔轮半径关系,就是要验证小球的角速度的关系,故要控制小球的质量与圆周运动的半径相同,测量出向心力的大小关系,由,得到角速度的关系,在根据,验证塔轮半径的关系。
图中两条曲线为相同半径、不同质量下向心力与角速度的关系图线,当角速度相同时由图可知,曲线对应的向心力小于曲线对应的向心力,
根据:,
可知曲线对应的金属块质量小于曲线对应的金属块质量。
12.【答案】解:探测器的轨道半径为,
探测器受到火星的万有引力大小;
探测器的运行过程中由万有引力提供向心力,则,
解得。
13.【答案】解:螺丝钉的线速度大小
螺丝钉做匀速圆周运动,螺丝钉受到的弹力提供向心力,
由牛顿第二定律得
解得
14.【答案】解:恰好能够沿半圆轨道运动,物块在点重力提供向心力,
由牛顿第二定律得
物块被弹出过程,弹簧的弹性势能转化为物块的动能,则
解得,
物块从第一次运动到过程,由动能定理得
在点,对物块,由牛顿第二定律得,
解得,
由牛顿第三定律可知,物块对轨道的压力大小,方向竖直向下
物块被挡板反弹后恰好不脱离轨道,物块从第一次到达点到恰好不脱离轨道过程,
由动能定理得
解得
则物块被挡板反弹后不脱离轨道,满足的条件是
15.【答案】解:整体根据平衡条件可得:
解得:;
若物块的质量为,软绳从静止开始下滑过程中,对整体根据动能定理可得:
解得:;
若物块的质量为,在软绳从静止开始到全部滑出滑轮的过程中,绳子重心下降:
对整体根据动能定理可得:
对物块,根据动能定理可得:
联立解得:。
第11页,共11页
一、单选题:本大题共10小题,共40分。
1.开普勒用年时间研究了丹麦一位天文学家的行星观测记录,最终发表了著名的开普勒三定律,这位天文学家是( )
A. 伽利略 B. 第谷 C. 托勒密 D. 哥白尼
2.下列选项中所运用的主要研究方法与卡文迪什测量引力常量的主要研究方法相同的是( )
A. 图甲中,通过平面镜的反射光线观察桌面的微小形变
B. 图乙中,利用作用效果相同研究合力与分力的关系
C. 图丙中,通过物体沿曲面运动研究重力做功的特点
D. 图丁中,利用该装置研究力与运动的关系
3.年月日,航天员王亚平再次进行太空授课,展示了一个奇妙现象:浸在水中的乒乓球因浮力消失而不会浮出水面下列说法正确的是( )
A. 水处于完全失重状态
B. 乒乓球不受任何力的作用
C. 乒乓球所受的合力为零
D. 在空间站若将装满水的杯子转动至杯口朝下,水会自动流出
4.旋转飞椅可简化成如图所示模型长为的钢绳一端系有质量为可视为质点的小球,另一端固定在直径为的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动当转盘匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向夹角为,不计钢绳的重力,此时钢绳的拉力为下列说法正确的是( )
A. 小球做圆周运动的半径为 B. 小球做圆周运动的轨迹圆心为点
C. 钢绳拉力的大小与向心力大小相等 D. 钢绳拉力沿水平方向的分力提供向心力
5.据报道,“天问一号”火星探测器以及“祝融号”火星车在年月份失联了一个月,失联的原因是由于太阳处在地球与火星中间,出现严重的“日凌干扰”现象,情景如图所示。已知地球、火星均沿轨道逆时针运动,地球公转周期为年,火星公转周期为年,试估算下次“日凌干扰”大约出现在
A. 年月 B. 年月 C. 年月 D. 年月
6.年月,“空中出租车”在上海试飞成功,完成首秀。质量为的“空中出租车”在竖直方向的牵引力作用下,从静止开始竖直上升,其运动图像如图所示,为匀加速阶段,时刻“空中出租车”达到功率并保持不变,运动过程中阻力大小恒定。下列说法正确的是( )
A. 整个过程牵引力保持不变 B. 过程,牵引力做功为
C. 阻力大小为 D. 时刻“空中出租车”的功率为
7.据报道,“恒星系统”由颗红矮星和颗如图所示围绕它运行的行星组成,若地球半径为,则行星的半径如下表。据推测行星和的密度大致相同,若行星的第一宇宙速度为,则行星的第一宇宙速度约为( )
行星
半径
A. B. C. D.
8.某种变速自行车有六个飞轮和三个链轮,链轮和飞轮的齿数如下表,前后轮直径为,人骑该车行进速度为,脚踩踏板做匀速圆周运动的最大角速度约为( )
名称 链轮 飞轮
齿数个
A. B. C. D.
9.竖直细圆杆顶端附近有一小孔,光滑细绳穿过小孔,细绳两端分别系有、两小球,已知球质量小于球质量。调节细绳并转动圆杆,使得两球与圆杆能以相同角速度在水平面内匀速转动,下列图样大致正确的是( )
A. B. C. D.
10.如图所示,质量为的小球从与轻弹簧上端相距处静止释放,弹簧的劲度系数为,重力加速度为,不计一切阻力,则小球在向下运动的过程中( )
A. 最大加速度为
B. 最大加速度小于
C. 最大速度为
D. 最大速度为
二、实验题:本大题共1小题,共15分。
11.某同学利用如图所示的向心力演示器探究小球做圆周运动的向心力与质量、运动半径和角速度之间的关系。
下列实验与本实验采用的研究方法相同的是____。
A.探究平抛运动的特点
B.探究小车速度随时间变化的规律
C.探究加速度与力、质量的关系
D.探究两个互成角度的力的合成规律
探究向心力和质量的关系时,将传动皮带套在半径相同的两塔轮轮盘上,应将质量不同的小球分别放在挡板_______处选填“和”、“和”、“和”。
实验中若将传动皮带套在半径不同的两塔轮轮盘上,是为了探究向心力大小与_______选填“角速度”、“半径”、“质量”的关系。
器材说明书上说第二层塔轮半径之比为:,如图所示在进行实验探究前,如果仅使用向心力演示仪来验证这个半径关系,你打算怎么做?___________________。
某兴趣小组用如图所示的传感器装置定量验证向心力的表达式。图中两条曲线为相同半径、不同质量下向心力与角速度的关系图线,可知曲线对应的金属块质量______选填“大于”、“小于”、“等于”曲线对应的金属块质量。
三、计算题:本大题共4小题,共45分。
12.随着航天科技的飞速发展,我国向火星发射多枚探测器。如图所示,假设质量为的某一探测器绕火星做匀速圆周运动。已知火星的质量为,半径为,探测器距离火星表面的高度也等于,万有引力常量为。求:
探测器受到火星的万有引力大小;
探测器的运行速度大小。
13.如图所示,飞轮半径为,质量为,为竖直转动轴。正常工作时转动轴受到的水平作用力可以认为是。如果高速转动的飞轮的重心不在转轴上,运行将不稳定,而且轴承会受到很大的作用力,加速磨损。假想在飞轮的边缘固定一个质量的小螺丝钉,此时飞轮转速为单位为。求:
螺丝钉的线速度大小;
转动轴受到的水平作用力的大小。
14.如图所示为某弹射装置的示意图。半径为的光滑半圆形轨道竖直固定放置,轨道最高点处有一弹射装置,轨道下端与水平轨道相切,水平轨道左侧处有一固定挡板未知且不为零。可视为质点的物块被弹簧弹射后从处进入半圆形轨道,恰好能够沿半圆轨道运动,进入水平轨道后与挡板发生弹性碰撞碰撞前后速度大小不变。已知物块的质量为,物块与水平轨道间的动摩擦因数为,重力加速度为。求:
初始时刻弹簧的弹性势能;
物块第一次到达圆轨道下端时对轨道的压力;
若物块被挡板反弹后不脱离轨道,则应满足什么条件。
15.如图所示,长为,质量为且质量分布均匀的软绳,放在长为的斜面上,斜面顶端有一个很小的固定滑轮,斜面倾角,软绳一端刚好接触滑轮,并通过一根轻绳跨过滑轮系着一物块,软绳恰好不下滑。忽略空气阻力,不计两绳与滑轮之间的摩擦,重力加速度为,软绳与斜面之间的动摩擦因数为,最大静摩擦力等于滑动摩擦力。
求物块的质量;
若物块的质量为,软绳从静止开始下滑,物块始终没有触碰到滑轮,求软绳下端滑至斜面底端时的速度大小;
若物块的质量为,软绳与滑轮平滑连接,在软绳从静止开始到全部滑出滑轮的过程中物块始终没有落地,求轻绳对物块做的功。
答案和解析
1.【答案】
【解析】解:开普勒仔细研究了丹麦天文学家第谷连续年对行星的观测结果,最终发表了著名的开普勒三定律。故ACD错误,B正确。
故选:。
2.【答案】
【解析】卡文迪什扭秤实验运用了放大的思想方法。图甲中,借助激光器及平面镜观察桌面微小形变运用了放大法;
图乙中,应用等效替代的实验方法;
图丙中,运用微元法的物理思想;
图丁中运用实验和逻辑推理相结合的方法,故A正确,BCD错误。
故选:。
3.【答案】
【解析】A.空间站中的物体都处于完全失重状态,水处于完全失重状态,故A正确;
乒乓球仍然受到地球引力的作用,由万有引力提供向心力,合力不为零,故BC错误;
D.由于空间站的物体处于完全失重状态,其万有引力用来提供向心力,装满水的杯子杯口朝下,水也不会流出,故D错误。
4.【答案】
【解析】小球以小球与转轴垂线交点为圆心做圆周运动,轨道半径为,故AB错误;
钢绳拉力的竖直方向分力与重力平衡,水平分力提供向心力,故C错误,D正确。
5.【答案】
【解析】设两次日凌干扰的时间间隔为,则有,已知年,年,
解得解得:年年,所以下次“日凌干扰”大约出现在年月,故ABD错误,故C正确。
6.【答案】
【解析】A.根据题意可知,匀加速过程牵引力保持不变,功率达到后牵引力逐渐减小,最后保持不变,故A错误;
B.过程,匀加速阶段功率小于,则整个过程中牵引力做功小于,故B错误;
当速度达到最大速度时,根据平衡条件有,
则阻力大小,
故C错误;
根据图像可知时刻“空中出租车”的速度为,
牵引力,
则该时刻的功率为 ,
故D正确。
故选:。
7.【答案】
【解析】行星的第一宇宙速度为,则有
可得第一宇宙速度
同理行星的第一宇宙速度为
,故B正确。
8.【答案】
【解析】当自行车行驶速度一定时,即后轮的角速度一定,飞轮的角速度一定,根据,由于脚踏板和链轮有相同的角速度,当脚踏板做匀速圆周运动的角速度最大时, 最少, 最多,即,,再由,可得。
故选B。
9.【答案】
【解析】两个小球均做匀速圆周运动,设其中一个小球悬线长为,悬线与杆的夹角为,小球的质量为,做匀速圆周运动的角速度为,受力情况如图所示:
根据牛顿第二定律可得:,解得:,由于相同,则相等,即悬线在竖直方向的分量相等,两个小球的轨迹平面在同一水平面内,故B正确、ACD错误。
故选:。
10.【答案】
【解析】、小球与弹簧相互作用时,牛顿第二定律,得,作出图像,围成面积的含义为,加速度减为零时,轴坐标为,速度最大,根据图像在第一象限围成面积,此时最大速度为,故D正确,C错误;
、小球最后速度为零,图像在第一象限围成面积与在第四象限围成面积相等,可得最大加速度大于,故AB错误。
11.【答案】;和;角速度;控制小球的质量与圆周运动的半径相同,测量出向心力的大小关系,由,得到角速度的关系,在根据,验证塔轮半径的关系;小于
【解析】本实验采用的研究方法是控制变量法,四个选项只有探究加速度与力、质量的关系的实验采用的是控制变量法,故C正确,ABD错误。
故选:。
探究向心力和质量的关系时,将传动皮带套在半径相同的两塔轮轮盘上,是控制角速度相同,还应控制小球做圆周运动的半径相同,故应将质量不同的小球分别放在挡板的和处。
若将传动皮带套在半径不同的两塔轮轮盘上,则小球的角速度不同,故是为了探究向心力大小与角速度的关系。
用向心力演示仪来验证这个塔轮半径关系,就是要验证小球的角速度的关系,故要控制小球的质量与圆周运动的半径相同,测量出向心力的大小关系,由,得到角速度的关系,在根据,验证塔轮半径的关系。
图中两条曲线为相同半径、不同质量下向心力与角速度的关系图线,当角速度相同时由图可知,曲线对应的向心力小于曲线对应的向心力,
根据:,
可知曲线对应的金属块质量小于曲线对应的金属块质量。
12.【答案】解:探测器的轨道半径为,
探测器受到火星的万有引力大小;
探测器的运行过程中由万有引力提供向心力,则,
解得。
13.【答案】解:螺丝钉的线速度大小
螺丝钉做匀速圆周运动,螺丝钉受到的弹力提供向心力,
由牛顿第二定律得
解得
14.【答案】解:恰好能够沿半圆轨道运动,物块在点重力提供向心力,
由牛顿第二定律得
物块被弹出过程,弹簧的弹性势能转化为物块的动能,则
解得,
物块从第一次运动到过程,由动能定理得
在点,对物块,由牛顿第二定律得,
解得,
由牛顿第三定律可知,物块对轨道的压力大小,方向竖直向下
物块被挡板反弹后恰好不脱离轨道,物块从第一次到达点到恰好不脱离轨道过程,
由动能定理得
解得
则物块被挡板反弹后不脱离轨道,满足的条件是
15.【答案】解:整体根据平衡条件可得:
解得:;
若物块的质量为,软绳从静止开始下滑过程中,对整体根据动能定理可得:
解得:;
若物块的质量为,在软绳从静止开始到全部滑出滑轮的过程中,绳子重心下降:
对整体根据动能定理可得:
对物块,根据动能定理可得:
联立解得:。
第11页,共11页
同课章节目录
