5.1.1 数列的概念 课件(共20张PPT)
文档属性
| 名称 | 5.1.1 数列的概念 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 662.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 10:14:17 | ||
图片预览








文档简介
(共20张PPT)
5.1.1 数列的概念
古希腊的毕达哥拉斯学派将1,4, 9,16等数称为正方形数,因为这些数目的点可以摆成一个正方形,如下图所示:依据这个规律我们很容易就能知道,下一个正方形数应该是25,再下一个是36,等等.
你知道吗?通过寻找数字出现的规律,可以产生新的发现.
1.理解数列的概念,了解数列的几种分类.
2.理解数列通项公式的概念及意义.
3.了解数列与函数的关系.
4.能够利用通项公式求数列的项,能够根据数列的已知项,求数列的通项公式.
探究 (1)我国古代哲学著作《庄子》中有一句话“一尺之棰,日取其半,万世不竭”.从数学上来说,如果木棍初始长度为1,则每天之后木棍的长度分别为
,,,… ①
(2)2009年至2015年,我国每一年专利申请受理数(精确到万)分别为
98,122,163,205,236,238,280. ②
(3)有些购物网站推出了分期付款服务,如图所示标价为3000元的电脑可以享受分期服务,不同的付款方式,所对应的付款总金额分别为
3000, 3045, 3090,3180,3360. ③
思考:上述①、②、③三个数列中的数有什么规律?
可否各自进行顺序交换?
一、数列
1.定义:一般地,我们把按照确定的顺序排列的一列数称为数列.
2.项:数列中的每一个数叫做这个数列的项.数列的第一个位置上的数叫做这个数列的第1项,常用符号a1表示;第二个位置上的数叫做这个数列的第2项,用a2表示……第n个位置上的数叫做这个数列的第n项,用an表示.其中第1项也叫做首项.
3.表示:数列的一般形式是a1,a2,…,an,…,简记为{an}.
点睛:(1)数列是按一定的“顺序”排列的一列数,有序性是数列的基本属性.数相同而顺序不同的数列是不相同的数列,例如1,2,3,…与3,2,1…就是不同的数列.
(2)符号{an}和an是不同的概念,{an}表示一个数列,而an表示数列中的第n项.
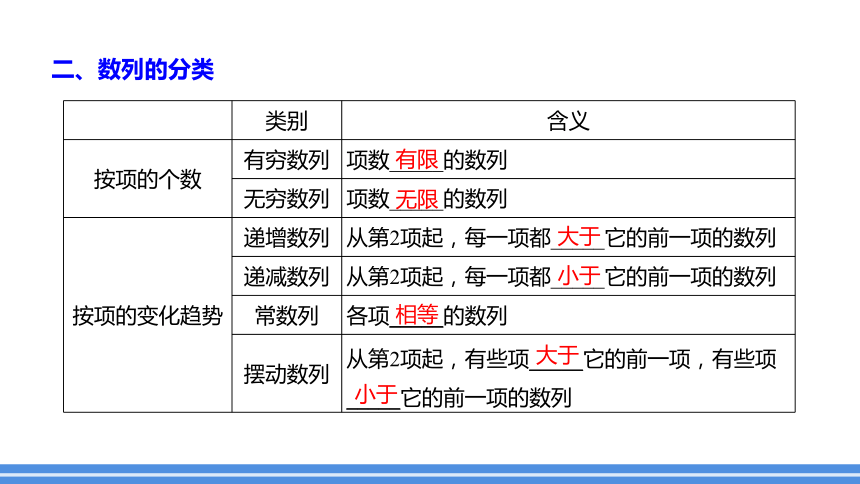
二、数列的分类
类别 含义
按项的个数 有穷数列 项数_____的数列
无穷数列 项数_____的数列
按项的变化趋势 递增数列 从第2项起,每一项都_____它的前一项的数列
递减数列 从第2项起,每一项都_____它的前一项的数列
常数列 各项_____的数列
摆动数列 从第2项起,有些项_____它的前一项,有些项
_____它的前一项的数列
有限
无限
大于
小于
相等
大于
小于
练习1. 判断下列数是不是数列,是的打“√”,错的打“×”.
(1)数列4,7,8,12是有穷数列,首项是4. ( )
(2)1,2,3,4和1,2,4,3是相同的数列. ( )
(3)同一个数在数列中不可能重复出现. ( )
(4) 1,2,3,4与 {1,2,3,4 }是同一数列. ( )
√
×
×
×
正确.
错误;数列具有顺序性.
错误;在数列的定义中并没有规定数必须不同.
错误;前一个是数列,后一个是集合.
三、数列的通项公式
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
点睛: (1)数列的通项公式实际上是一个以正整数集N*(或它的有限子集){1,2,…,n}为定义域的函数表达式.
(2)并不是所有的数列都有通项公式.
(3)同一数列的通项公式,其表达形式可以是不唯一的,例如数列-1,1,-1,1,-1,1,…的通项公式可以写成an=(-1)n,an=(-1)n+2,an=cos nπ等.
例 1:根据下列数列的通项公式,写出数列的第2项和第5项.
(1) (2) .
解:只要用序号代替公式中的便可,相当于给出函数解析式求函数值.
(1)求解数列的第2项,则,将其代入 1.
同理 .
(2) 0.
例 2:写出以下各数列{}的一个通项公式.
(1)2,4,6,8,10, … ;
(2)1,3,5,7,9, … ;
(3)0,2,0,2,0, … ;
(4),,,, , … .
解:观察、分析,寻找数列的每一项与其所在项的序号之间的关系.
例 2:写出以下各数列{an}的一个通项公式:
2,4,6,8,…, (2) 1,3,5,7,9,…,
(3)0,2,0,2,0,…, (4)
解:(1)观察数列的前5项可知,每一项都是序号的2倍,因此数列的一个通项公式为an=2n.
(2)因为这个数列每一项都比(1)中小1,因此数列的一个通项公式为an=2n-1
(3)因为数列的第1,3,5项都是0,而第2,4项都是2.因此它的一个通项公式为
an=.
例 2:写出以下各数列{an}的一个通项公式:
2,4,6,8,…, (2) 1,3,5,7,9,…,
(3)0,2,0,2,0,…, (4)
(4)此题可分段考虑,
首先是符号,因为负号、正号是交替出现的,可乘解决;
其次是分子,数列每一项的分子构成的数列是2,4,6,8,10,…,其中每一个数都是序号的2倍,可用表示;
最后是分母,数列每一项的分母都是分子的平方减去1,可用表示
因此它的一个通项公式为=
方法归纳
根据数列的前几项写通项公式的具体思路为:
(1)先统一项的结构,如都化成分数、根式等.
(2)分析这一结构中变化的部分与不变的部分,探索变化部分的规律与对应序号间的关系.
(3)对于符号交替出现的情况,可先观察其绝对值,再用(-1)k处理符号.
(4)对于周期出现的数列,考虑利用周期函数的知识解答.
常见数列的通项公式
数列 通项公式
1,2,3,4,…
1,3,5,7,…
2,4,6,8,…
1,4,9,16,…
1,2,4,8,…
-1,1,-1,1,…
9,99,999,9999,…
1,,,,…
探究 (1)已知函数你能根据这个函数构造出一个数列吗?
(2)你能总结出一般数列与函数的关系吗?
分析:令=1,2,3,4,…,n…,
可得到数列2,,1,…,,….,
即这个数列的通项公式是.
四、数列与函数
数列{an}是从正整数集N*(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
另一方面,对于函数y=f(x),如果f(n)(n∈N*)
有意义,那么_____________________________
构成了一个数列{f(n)}.
f(1),f(2),…,f(n),…
例 3:已知函数设数列{an}的通项公式为an=其中n∈N*
(1)求证:<1;
(2)判断{an}是递增数列还是递减数列,并说明理由.
解:(1)由题意可知an=又因为n∈N* ,所以0<,因此<1;即<1.
(2)因为= ( )(
又因为> ,所以>0,
从而>0,即,
因此{an}是递增数列.
方法归纳
数列增减性的判定方法
(1)作差比较法
①若an+1-an>0恒成立,则数列{an}是递增数列;
②若an+1-an<0恒成立,则数列{an}是递减数列;
③若an+1-an=0恒成立,则数列{an}是常数列.
(2)作商比较法
类别 >1 0<<1 =1
an>0 递增数列 递减数列 常数列
an<0 递减数列 递增数列 常数列
1.以下四个数中,哪个数是数列{n(n+1)}中的一项 ( )
A.380 B.39 C.32 D.23
2.已知数列{an}中,an=-2n2+31n+9(n∈N+),则{an}中的最大项为 .
3.下列数列的一个通项公式: .
A
129
5.1.1 数列的概念
古希腊的毕达哥拉斯学派将1,4, 9,16等数称为正方形数,因为这些数目的点可以摆成一个正方形,如下图所示:依据这个规律我们很容易就能知道,下一个正方形数应该是25,再下一个是36,等等.
你知道吗?通过寻找数字出现的规律,可以产生新的发现.
1.理解数列的概念,了解数列的几种分类.
2.理解数列通项公式的概念及意义.
3.了解数列与函数的关系.
4.能够利用通项公式求数列的项,能够根据数列的已知项,求数列的通项公式.
探究 (1)我国古代哲学著作《庄子》中有一句话“一尺之棰,日取其半,万世不竭”.从数学上来说,如果木棍初始长度为1,则每天之后木棍的长度分别为
,,,… ①
(2)2009年至2015年,我国每一年专利申请受理数(精确到万)分别为
98,122,163,205,236,238,280. ②
(3)有些购物网站推出了分期付款服务,如图所示标价为3000元的电脑可以享受分期服务,不同的付款方式,所对应的付款总金额分别为
3000, 3045, 3090,3180,3360. ③
思考:上述①、②、③三个数列中的数有什么规律?
可否各自进行顺序交换?
一、数列
1.定义:一般地,我们把按照确定的顺序排列的一列数称为数列.
2.项:数列中的每一个数叫做这个数列的项.数列的第一个位置上的数叫做这个数列的第1项,常用符号a1表示;第二个位置上的数叫做这个数列的第2项,用a2表示……第n个位置上的数叫做这个数列的第n项,用an表示.其中第1项也叫做首项.
3.表示:数列的一般形式是a1,a2,…,an,…,简记为{an}.
点睛:(1)数列是按一定的“顺序”排列的一列数,有序性是数列的基本属性.数相同而顺序不同的数列是不相同的数列,例如1,2,3,…与3,2,1…就是不同的数列.
(2)符号{an}和an是不同的概念,{an}表示一个数列,而an表示数列中的第n项.
二、数列的分类
类别 含义
按项的个数 有穷数列 项数_____的数列
无穷数列 项数_____的数列
按项的变化趋势 递增数列 从第2项起,每一项都_____它的前一项的数列
递减数列 从第2项起,每一项都_____它的前一项的数列
常数列 各项_____的数列
摆动数列 从第2项起,有些项_____它的前一项,有些项
_____它的前一项的数列
有限
无限
大于
小于
相等
大于
小于
练习1. 判断下列数是不是数列,是的打“√”,错的打“×”.
(1)数列4,7,8,12是有穷数列,首项是4. ( )
(2)1,2,3,4和1,2,4,3是相同的数列. ( )
(3)同一个数在数列中不可能重复出现. ( )
(4) 1,2,3,4与 {1,2,3,4 }是同一数列. ( )
√
×
×
×
正确.
错误;数列具有顺序性.
错误;在数列的定义中并没有规定数必须不同.
错误;前一个是数列,后一个是集合.
三、数列的通项公式
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
点睛: (1)数列的通项公式实际上是一个以正整数集N*(或它的有限子集){1,2,…,n}为定义域的函数表达式.
(2)并不是所有的数列都有通项公式.
(3)同一数列的通项公式,其表达形式可以是不唯一的,例如数列-1,1,-1,1,-1,1,…的通项公式可以写成an=(-1)n,an=(-1)n+2,an=cos nπ等.
例 1:根据下列数列的通项公式,写出数列的第2项和第5项.
(1) (2) .
解:只要用序号代替公式中的便可,相当于给出函数解析式求函数值.
(1)求解数列的第2项,则,将其代入 1.
同理 .
(2) 0.
例 2:写出以下各数列{}的一个通项公式.
(1)2,4,6,8,10, … ;
(2)1,3,5,7,9, … ;
(3)0,2,0,2,0, … ;
(4),,,, , … .
解:观察、分析,寻找数列的每一项与其所在项的序号之间的关系.
例 2:写出以下各数列{an}的一个通项公式:
2,4,6,8,…, (2) 1,3,5,7,9,…,
(3)0,2,0,2,0,…, (4)
解:(1)观察数列的前5项可知,每一项都是序号的2倍,因此数列的一个通项公式为an=2n.
(2)因为这个数列每一项都比(1)中小1,因此数列的一个通项公式为an=2n-1
(3)因为数列的第1,3,5项都是0,而第2,4项都是2.因此它的一个通项公式为
an=.
例 2:写出以下各数列{an}的一个通项公式:
2,4,6,8,…, (2) 1,3,5,7,9,…,
(3)0,2,0,2,0,…, (4)
(4)此题可分段考虑,
首先是符号,因为负号、正号是交替出现的,可乘解决;
其次是分子,数列每一项的分子构成的数列是2,4,6,8,10,…,其中每一个数都是序号的2倍,可用表示;
最后是分母,数列每一项的分母都是分子的平方减去1,可用表示
因此它的一个通项公式为=
方法归纳
根据数列的前几项写通项公式的具体思路为:
(1)先统一项的结构,如都化成分数、根式等.
(2)分析这一结构中变化的部分与不变的部分,探索变化部分的规律与对应序号间的关系.
(3)对于符号交替出现的情况,可先观察其绝对值,再用(-1)k处理符号.
(4)对于周期出现的数列,考虑利用周期函数的知识解答.
常见数列的通项公式
数列 通项公式
1,2,3,4,…
1,3,5,7,…
2,4,6,8,…
1,4,9,16,…
1,2,4,8,…
-1,1,-1,1,…
9,99,999,9999,…
1,,,,…
探究 (1)已知函数你能根据这个函数构造出一个数列吗?
(2)你能总结出一般数列与函数的关系吗?
分析:令=1,2,3,4,…,n…,
可得到数列2,,1,…,,….,
即这个数列的通项公式是.
四、数列与函数
数列{an}是从正整数集N*(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
另一方面,对于函数y=f(x),如果f(n)(n∈N*)
有意义,那么_____________________________
构成了一个数列{f(n)}.
f(1),f(2),…,f(n),…
例 3:已知函数设数列{an}的通项公式为an=其中n∈N*
(1)求证:<1;
(2)判断{an}是递增数列还是递减数列,并说明理由.
解:(1)由题意可知an=又因为n∈N* ,所以0<,因此<1;即<1.
(2)因为= ( )(
又因为> ,所以>0,
从而>0,即,
因此{an}是递增数列.
方法归纳
数列增减性的判定方法
(1)作差比较法
①若an+1-an>0恒成立,则数列{an}是递增数列;
②若an+1-an<0恒成立,则数列{an}是递减数列;
③若an+1-an=0恒成立,则数列{an}是常数列.
(2)作商比较法
类别 >1 0<<1 =1
an>0 递增数列 递减数列 常数列
an<0 递减数列 递增数列 常数列
1.以下四个数中,哪个数是数列{n(n+1)}中的一项 ( )
A.380 B.39 C.32 D.23
2.已知数列{an}中,an=-2n2+31n+9(n∈N+),则{an}中的最大项为 .
3.下列数列的一个通项公式: .
A
129
