6.3 利用导数解决实际问题 课件(共17张PPT)
文档属性
| 名称 | 6.3 利用导数解决实际问题 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 10:32:03 | ||
图片预览






文档简介
(共17张PPT)
6.3 利用导数解决实际问题
1.了解导数在解决利润最大、效率最高、用料最省、成本最低等实际问题中的作用.
2.能利用导数求出某些实际问题的最大值(最小值).
用料最省
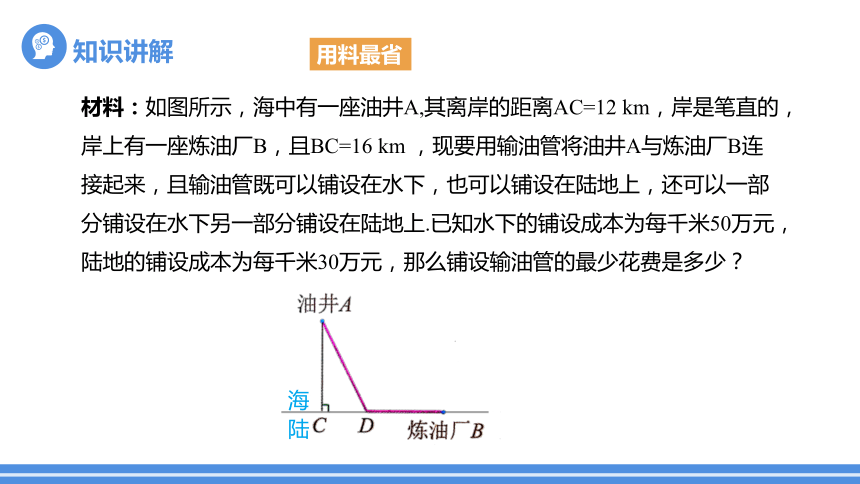
材料:如图所示,海中有一座油井A,其离岸的距离AC=12 km,岸是笔直的,岸上有一座炼油厂B,且BC=16 km ,现要用输油管将油井A与炼油厂B连接起来,且输油管既可以铺设在水下,也可以铺设在陆地上,还可以一部分铺设在水下另一部分铺设在陆地上.已知水下的铺设成本为每千米50万元,陆地的铺设成本为每千米30万元,那么铺设输油管的最少花费是多少?
海
陆
探究1. 分别计算下列两种算法的铺设成本,然后尝试给出最优的铺设方案
(1)先沿AC铺设,再沿CB铺设;
(2)直接沿着线段AB铺设.
如果先沿AC铺设,再沿CB铺设,则成本为(万元).
又因为
所以直接沿线段AB铺设,成本为 2×50=100(万元).
海
陆
记先沿AD铺设再沿DB铺设输油管时成本为万元,则
1.6
因此,当 时,
令 可解得
可知在上递减,在上递增,从而在时取得最小值,而且最小值为1.6 最少花费是96万元.
如图所示,在岸上取一点D,设计其距离C的距离为则
, 1.6
海
陆
归纳总结
解决优化问题的注意点
利用导数解优化问题,往往转化为求函数的最大值或最小值问题,解题时要特别注意以下几点:
(1)当问题涉及多个变量时,应根据题意分析它们的关系,找出变量之间的关系式;
(2)确定函数关系式中自变量的取值范围;
(3)所得的结果要符合问题的实际意义.
利润最大
材料:某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销.经试销发现:日销售量Q(件)与实际销售价x(元/件)满足关系:
Q=
(1)求总利润(利润=销售额-成本)y(元)与销售价x(元/件)的函数关系式;
(2)当实际销售价为多少时总利润最大.
解:(1)根据题意得,总利润y(元)与销售价x(元/件)的函数关系式是
y=
=
(2)由(1)得①当5则y′=234(x2-13x+42)=234(x-6)(x-7).
当50,y为增函数;
当6∴ 当x=6时,ymax=195.
②当7≤x<8时,y=6(33-x)∈(150,156].
③当8≤x<13时,y=-10(x-9)2+160,
∴ 当x=9时,ymax=160.
综上,当x=6时,总利润最大,即当实际销售价为6元/件时总利润最大.
效率最高
材料:如图所示,某海岛码头O离岸边最近点B的距离是150 km,岸边的医药公司A与点B的距离为300km,现有一批药品要尽快送达海岛码头,已知A与B之间有一条公路,现要用海陆联运的方式运送这批药品,若汽车的时速为130km,快艇时速为50km. 试在岸边选一点C,先将药品用汽车从A送到C,再用快艇从C运到海岛码头,则点C选在何处可使运输时间最短?
因为
令可解得,
因此可知在上递减,在上递增,
从而在时取得最小值. 这就是说,点C选在离点B点为时可使运输时间最短.
解:设点C与点B的距离为km,运输时间为T()小时,则
.
成本最低
材料:已知某种工艺品总成本C元是产量Q件的函数,且
将Q看成能取区间[1, 30]内的每一个值,求月产量Q为多少时,才能使每件产品的平均成本最低?最低平均成本为多少?
解:记平均成本为元,则
=
因为时,有 令,可解得
因此可知在上递减,在上递增,从而在 Q=10时取得极小值,而且在此事取得最小值
=
及当月产量为10万件,是每件产品的平均成本最低最低为400元.
归纳总结
利用导数解最优化问题的一般步骤
(1)抽象出实际问题的数学模型,列出函数解析式,标明自变量的取值范围;
(2)求导数 并解方程,即求出函数可能的极值点;
(3)比较函数在区间端点的函数值与极值的大小,得出函数最值;
(4)根据实际问题的意义,给出相应答案.
1.某生产厂家生产一种产品的固定成本为1万元,并且每生产1百台产品需增加投入0.5万元. 已知销售收入R(x)(万元)满足R(x)=x3x2x(其中x是该产品的月产量,单位:百台,06
2.某工厂生产某种产品,已知该产品的月产量x(吨)与产品的价格P(元/吨)之间的
关系为P=24200-x2,且生产x吨的成本为R=50000+200x元. 问每月生产多少吨产
品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
解:每月生产x吨时的利润为
f (x)=(24200-x2)x-(50000+200x)=-x3+24000x-50000(x≥0).
由f (x)=-x2+24000=0,解得x1=200,x2=-200(舍去).
因为f (x)在[0,+∞)内只有一个极大值点x=200使f (x)=0,故它就是最大值点,
且最大值为f (200)=-×2003+24000×200-50000=3150000(元).
所以每月生产200吨产品时利润达到最大,最大利润为315万元.
最优化问题
用函数表示问题
用导数解决问题
最优化问题答案
6.3 利用导数解决实际问题
1.了解导数在解决利润最大、效率最高、用料最省、成本最低等实际问题中的作用.
2.能利用导数求出某些实际问题的最大值(最小值).
用料最省
材料:如图所示,海中有一座油井A,其离岸的距离AC=12 km,岸是笔直的,岸上有一座炼油厂B,且BC=16 km ,现要用输油管将油井A与炼油厂B连接起来,且输油管既可以铺设在水下,也可以铺设在陆地上,还可以一部分铺设在水下另一部分铺设在陆地上.已知水下的铺设成本为每千米50万元,陆地的铺设成本为每千米30万元,那么铺设输油管的最少花费是多少?
海
陆
探究1. 分别计算下列两种算法的铺设成本,然后尝试给出最优的铺设方案
(1)先沿AC铺设,再沿CB铺设;
(2)直接沿着线段AB铺设.
如果先沿AC铺设,再沿CB铺设,则成本为(万元).
又因为
所以直接沿线段AB铺设,成本为 2×50=100(万元).
海
陆
记先沿AD铺设再沿DB铺设输油管时成本为万元,则
1.6
因此,当 时,
令 可解得
可知在上递减,在上递增,从而在时取得最小值,而且最小值为1.6 最少花费是96万元.
如图所示,在岸上取一点D,设计其距离C的距离为则
, 1.6
海
陆
归纳总结
解决优化问题的注意点
利用导数解优化问题,往往转化为求函数的最大值或最小值问题,解题时要特别注意以下几点:
(1)当问题涉及多个变量时,应根据题意分析它们的关系,找出变量之间的关系式;
(2)确定函数关系式中自变量的取值范围;
(3)所得的结果要符合问题的实际意义.
利润最大
材料:某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销.经试销发现:日销售量Q(件)与实际销售价x(元/件)满足关系:
Q=
(1)求总利润(利润=销售额-成本)y(元)与销售价x(元/件)的函数关系式;
(2)当实际销售价为多少时总利润最大.
解:(1)根据题意得,总利润y(元)与销售价x(元/件)的函数关系式是
y=
=
(2)由(1)得①当5
当5
当6
②当7≤x<8时,y=6(33-x)∈(150,156].
③当8≤x<13时,y=-10(x-9)2+160,
∴ 当x=9时,ymax=160.
综上,当x=6时,总利润最大,即当实际销售价为6元/件时总利润最大.
效率最高
材料:如图所示,某海岛码头O离岸边最近点B的距离是150 km,岸边的医药公司A与点B的距离为300km,现有一批药品要尽快送达海岛码头,已知A与B之间有一条公路,现要用海陆联运的方式运送这批药品,若汽车的时速为130km,快艇时速为50km. 试在岸边选一点C,先将药品用汽车从A送到C,再用快艇从C运到海岛码头,则点C选在何处可使运输时间最短?
因为
令可解得,
因此可知在上递减,在上递增,
从而在时取得最小值. 这就是说,点C选在离点B点为时可使运输时间最短.
解:设点C与点B的距离为km,运输时间为T()小时,则
.
成本最低
材料:已知某种工艺品总成本C元是产量Q件的函数,且
将Q看成能取区间[1, 30]内的每一个值,求月产量Q为多少时,才能使每件产品的平均成本最低?最低平均成本为多少?
解:记平均成本为元,则
=
因为时,有 令,可解得
因此可知在上递减,在上递增,从而在 Q=10时取得极小值,而且在此事取得最小值
=
及当月产量为10万件,是每件产品的平均成本最低最低为400元.
归纳总结
利用导数解最优化问题的一般步骤
(1)抽象出实际问题的数学模型,列出函数解析式,标明自变量的取值范围;
(2)求导数 并解方程,即求出函数可能的极值点;
(3)比较函数在区间端点的函数值与极值的大小,得出函数最值;
(4)根据实际问题的意义,给出相应答案.
1.某生产厂家生产一种产品的固定成本为1万元,并且每生产1百台产品需增加投入0.5万元. 已知销售收入R(x)(万元)满足R(x)=x3x2x(其中x是该产品的月产量,单位:百台,0
2.某工厂生产某种产品,已知该产品的月产量x(吨)与产品的价格P(元/吨)之间的
关系为P=24200-x2,且生产x吨的成本为R=50000+200x元. 问每月生产多少吨产
品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
解:每月生产x吨时的利润为
f (x)=(24200-x2)x-(50000+200x)=-x3+24000x-50000(x≥0).
由f (x)=-x2+24000=0,解得x1=200,x2=-200(舍去).
因为f (x)在[0,+∞)内只有一个极大值点x=200使f (x)=0,故它就是最大值点,
且最大值为f (200)=-×2003+24000×200-50000=3150000(元).
所以每月生产200吨产品时利润达到最大,最大利润为315万元.
最优化问题
用函数表示问题
用导数解决问题
最优化问题答案
