2024-2025学年吉林省松原市前郭县达里巴乡中学八年级期中检测数学试卷(图片版,含答案)
文档属性
| 名称 | 2024-2025学年吉林省松原市前郭县达里巴乡中学八年级期中检测数学试卷(图片版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 00:00:00 | ||
图片预览


文档简介
前郭县达里巴乡中学·八年级期中检测卷 二、填空题(每题 3分,共 15分)
3
数学试卷 7.若代数式 在实数范围内有意义,则 x的取值范围为___________.x 1
1. 120 120 8.在矩形 ABCD中,E为边 AD的中点,F为边 BC上的一点,连接 EF ,DF ,若 AB 4 ,BC 8 ,EF 5 ,则本试卷为数学科目,考试形式为闭卷,全卷满分 分,考试时间 分钟,请合理安排答题时间。
2. DF ______.答题前,请务必将自己的姓名、班级、考号等信息准确填写在答题卡和试卷相应位置。
3.选择题答案须用 2B铅笔规范填涂在答题卡上,非选择题请用黑色字迹的钢笔或签字笔作答,答案必须写在 9.如图,在矩形 ABCD中, AB 3 , BC 2 ,M是 AD边的中点,N是 AB边上的动点,将△AMN沿 MN所在
答题卡指定区域内,写在试卷上无效。 直线折叠,得到△A MN ,连接 A C ,则 A C的最小值是______.
4.闭卷考试不允许查阅教材及相关资料,请独立思考、诚信作答,禁止交流讨论、传递资料等作弊行为。
5.答题时请注意字迹工整、卷面整洁,合理组织语言,条理清晰地表达观点。
6.考试结束后,请将试卷和答题卡一并交回,不得带出考场。
一、单选题(每题 3 分,共 18分)
1.下列二次根式中,与 2是同类二次根式的是( ) 第九题图 第十题图 第十一题图
A. 4 B. 6 C. 8 D. 12 10.如图, ABCD的周长为 36,对角线 AC,BD相交于点 O.点 E是 CD的中点, BD 12 ,则△DOE的周长
2.勾股数,又名毕达哥拉斯三元数,是指可以构成一个直角三角形三边的一组正整数.下列各组数中 为______.
是勾股数的是( ) 11.我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由
A.0.6,0.8,1 B.1,3,10 C.5,10,12 D.3,4,5 商高发现,故又称之为“商高定理”.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼
3.矩形具有而平行四边形不一定具有的性质是( ) 成的一个大正方形,若大正方形的面积是 25,小正方形的面积是 1,直角三角形的两条直角边长分别为
A.对边相等 B.对角相等 m、n,则mn ______.
C.对角线相等 D.对角线互相平分
4.如图,在矩形 ABCD中,对角线 AC , BD相关于点 O,E为边CD上的任意一点(不与点 C,D重合),过点 E 三、解答题(12—14每题6分,15—17每题7分,18—19每题8分,20—21每题10分,22题12分,共87分)
作 EF BD , EG AC ,垂足分别为 F,G,若 AB 8 ,BC 6 ,则EF EG的值为( )
12.(6分)已知: x 1 2 , y 1 2 ,求 x2 y2 xy 2x 2y 的值.
A. 24 B.12 C.5 D.6
5 5
5.a、b 2 2、c为△ABC三边,不是直角三角形的是( ) 13.(6分)已知 a 2 5,b 2 5 ,求代数式 a b ab 的值.
A.a2 c2 b2 B. a 5 3 ,b 1, c
4 4
C. A : B : C 3 : 4 : 5 D. a 8k ,b 17k , c 15k
6.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形 ABCD和 EFGH .连接EG , BD相交于点
O, BD S与HC相交于点 P.若GO GP ,则 △ABD 的值是( )
S△EFG
a 1 a2 1
14.(6分)先化简,再求值: 2 a ,其中a 1 2 .a 2a 1 a 1
A.1 2 B. 2 2 C.5 2 D.15
4
第 1页 共 4页
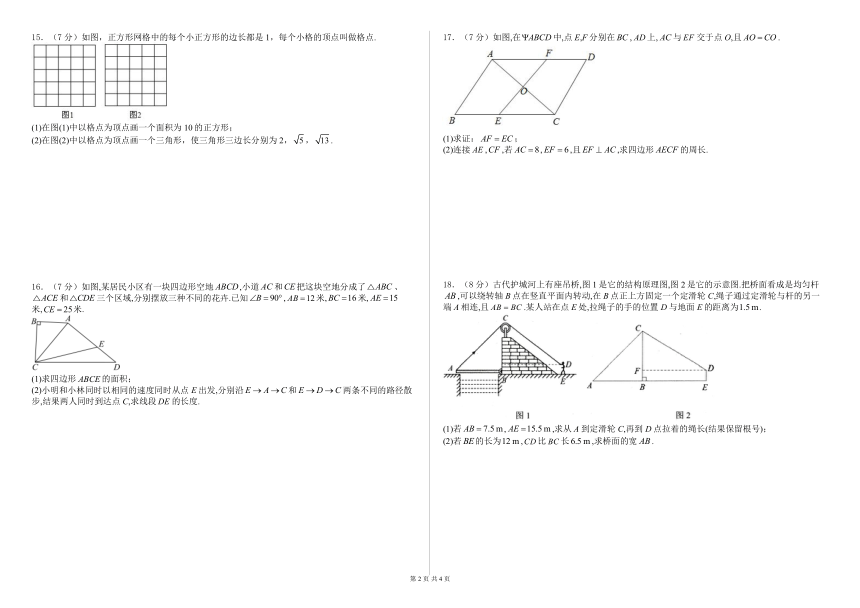
15.(7分)如图,正方形网格中的每个小正方形的边长都是 1,每个小格的顶点叫做格点. 17.(7分)如图,在 ABCD中,点 E,F分别在BC , AD上, AC与 EF 交于点 O,且 AO CO .
(1)在图(1)中以格点为顶点画一个面积为 10的正方形;
(2)在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为 2, 5, 13 . (1)求证: AF EC;
(2)连接 AE ,CF ,若 AC 8 ,EF 6 ,且EF AC ,求四边形 AECF的周长.
16.(7分)如图,某居民小区有一块四边形空地 ABCD ,小道 AC和CE把这块空地分成了△ABC、 18.(8分)古代护城河上有座吊桥,图 1是它的结构原理图,图 2是它的示意图.把桥面看成是均匀杆
△ACE和△CDE三个区域,分别摆放三种不同的花卉.已知 B 90 , AB 12米,BC 16米, AE 15 AB ,可以绕转轴 B点在竖直平面内转动,在 B点正上方固定一个定滑轮 C,绳子通过定滑轮与杆的另一
米,CE 25米. 端 A相连,且 AB BC .某人站在点 E处,拉绳子的手的位置 D与地面 E的距离为1.5m .
(1)求四边形 ABCE的面积;
(2)小明和小林同时以相同的速度同时从点 E出发,分别沿E A C和E D C两条不同的路径散
步,结果两人同时到达点 C,求线段DE的长度.
(1)若 AB 7.5 m , AE 15.5 m ,求从 A到定滑轮 C,再到 D点拉着的绳长(结果保留根号);
(2)若BE的长为12 m ,CD比 BC长6.5m ,求桥面的宽 AB .
第 2页 共 4页
19.(8分)怀仁市为做好城市园林绿化工作,进一步改善城市生态环境,美化城市居住环境,提升 20.(10 分)综合与实践
人民群众获得感、幸福感、对市内绿地进行改建.如图,该市某公园有一块长方形绿地 ABCD, AB的长 【背景介绍】勾股定理是几何学中的明珠,充满着魅力.勾股定理是用代数思想解决几何问题的最重要
为2 13m,BC的长为3 13 m,绿地内有一块长方形花坛(图中阴影部分),长为 4 2 2 m,宽为 的工具之一,它不但因验证方法层出不穷吸引着人们,更因为应用广泛而使人着迷.
【验证方法】如图①是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以验证勾股定理.
4 2 2 m . 思路:大正方形的面积有两种求法,一种是等于 c2 .另一种是等于四个直角三角形与一个小正方形的面
1
积之和,即 ab 4 1 b a 2 2,从而得到等式c2 ab 4 b a .化简便得结论 a2 b2 c2 .
2 2
这种用两种求法表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
(1)求长方形 ABCD的周长;
(2)除花坛外的绿地(图中空白部分)另作他用,需要 40元 /m2的定期维护费,求定期维护的总费用.
(1)【方法应用】千百年来,人们对勾股定理的验证趋之若鹜,其中有著名的数学家,也有业余数学爱
好者.美国第 20任总统詹姆斯·伽菲尔德利用图②验证了勾股定理:把两个全等的直角三角形如图②所
示放置,请根据图形面积之间的关系,验证勾股定理a2 b2 c2 .
(2)【方法迁移】请利用“双求法”解决下面的问题:如图③,在△ABC中, AD是BC边上的高,
AB 4, AC 5,BC 6,设BD x,求 x的值.
(3)【数学思想】在解决以上问题的过程中,让我们感悟的数学思想有___________.(填序号)
①方程思想②数形结合思想③分类讨论思想
第 3页 共 4页
21.(10 分) 22.(12 分)如图,在△ABC中, A 90 , AB 2, AC 4,点 D为边 AC的中点.动点 P从点 A
如图,已知正方形 ABCD的边长为 2,点 E是边 CD上的一动点,AF平分 BAE交边 BC于点 F. 出发,沿折线 AB BC向点 C运动,点 P在 AB上以每秒 1个单位长度的速度运动,在BC上以每秒
5个单位长度的速度运动.在点 P运动过程中,连接 PD,将△APD沿 PD翻折得到△A PD .设点 P的
运动时间为 t秒 0 t 4 .
(1)①当点 F恰好是边 BC的中点时,求线段 DE长;
②当点 E恰好是边 CD的中点时,求线段 BF长. (1)BC的长为______.
(2)猜想线段 AE,DE,BF之间的数量关系,并说明理由. (2)用含 t的代数式表示线段BP的长.
(3)直接写△ADE与△ABF面积和的最大值. (3)当四边形 APA D为中心对称图形时,求 t的值.
(4)连结 AA ,当 AA D与 B相等时,直换写出 t的值.
第 4页 共 4页
达里巴中学·八年级数学 又∵ DBC 45 , 故答案为: 65 或 17 .
∴ GBC 22.5 ,
参考答案 9.答案: 10 1∴ PBG GBC , 10.答案:15
1.答案:C ∵ BGP BGC 90 ,BG BG , 11.答案:12
2.答案:D ∴△BPG≌△BCG(ASA) , 解析:∵大正方形的面积是 25,
3.答案:C ∴PG CG . ∴m2 n2 25 ,
4.答案:A 设OG PG CG x , ∵小正方形的面积是 1,
解析:连接OE ,如图: ∵O为 EG,BD的交点,
∴ m n 2 1,
∴EG 2x ,FG 2x ,
∴m2 2mn n2 1 ,
∵四个全等的直角三角形拼成“赵爽弦图”,
∴BF CG x , ∴25 2mn 1 ,
∴2mn 24 ,
∴BG x 2x ,
∴mn 12 ,
∴BC 2 BG2 CG2 x2 ( 2 1)2 x2 (4 2 2)x2 , 故答案为:12.
∵四边形 ABCD是矩形, S△ABD S= 正方形ABCD (4 2 2)x
2
∴ 12.答案:7 4 22 2 2 .
∴ ABC 90 ,OA OC ,OB OD , AC BD , S△EFG S正方形EFGH 2x 解析:∵ x 1 2 , y 1 2 ,
∴OD OC , AC AB2 BC2 62 82 10 , 故选:B. ∴ x y (1 2) (1 2) 2 2
7.答案: x 1
∴ S ABCD AB·BC
1
48 , S△DOC S ,OD OC 5 ,
xy (1 2)(1 2) 1
矩形 4 矩形ABCD
12 8.答案: 65 或 17
∴ x2 y2 xy 2x 2y
∴ 解析:①如图所示,当BF CF时,过 F作FG AD于 G,则 2
S S S 1OD·EF 1
GF AB 4 , x y 2 x y xy
△DOC △DOE △COE OC·EG
1
OD FE 1 EG 5 EF EG 12
2 2 2 2 ( 2 2)2 2 ( 2 2) ( 1)
, 7 4 2 .
∴ EF 24 EG ; 13.答案:-4
5 解析: a2b ab2 ab(a b)
故选:A.
C (2 5)(2 5)(2 5 2 5)5.答案:
解析:A、∵a2 c2 b2 ,∴a2 b2 c2 ,∴a、b、c为△ABC三边, 在Rt△EFG中,EG 52 42 3 ,
1 4 4.
E AD , AD BC 8 , 故代数式的值为-4是直角三角形,故本选项错误; 又∵ 是 的中点
2 2 2 1 2B、∵b c a ,∴a、b、c 为△ABC三边,是直角三角形,故本 ∴DE 4 , 14.答案: , 1
∴DG 4 3 1, a 1 2选项错误;
15.答案:(1)详见解析;(2)详见解析.
C、∵ A : B : C 3 : 4 : 5 ,∴设 A 3x ,则 B 4x , C 5x , ∴Rt△DFG中,DF 42 12 17 ; (1)如图 1 所示:正方形 ABCD 即为所求;
∵ A B C 180 ,即3x 4x 5x 180 ,解得, x 15 , ②如图所示,当BF CF时,过 F作FG AD于 G,则GF AB 4 , (2)如图 2 所示:三角形 ABC 即为所求.
∴5x 5 15 75 90 ,∴a、b、c为△ABC三边,不是直角三
角形,故本选项正确;
D、∵a2 c2 b2 ,∴a、b、c为△ABC三边,是直角三角形,故本
选项错误.
故选:C.
6.答案:B
解析:∵四边形 EFGH 2为正方形, 在Rt△EFG中,EG 5 4 3 ,
∴ EGH 45 , FGH 90 , 又∵E是 AD的中点, AD BC 8 ,
∵OG GP , ∴DE 4 ,
∴ GOP OPG 67.5 , ∴DG 4 3 7 ,
∴ PBG 22.5 , ∴Rt△DFG中,中,DF 42 72 65 , 16.答案:(1) 246平方米
(2)线段DE的长度为 6 米 C
菱形AECF 20; (3)①②
解析:(1)∵ B 90 , AB 12米, BC 16米 15 a b(1) a b 18.答案:(1) 2 10 解析: 证明:观察图形可知 S
AC AB2 BC2 20 2 梯形ACED
或
∴ 米 2
∵ AC 2 AE 2 202 152 625 252 CE 2 (2) 6.5 S 1 S S S ab+ 1 ab 1 c2 .
∴△ACE是直角三角形,且 CAE 90 解析:(1)依题意得:DFBE是矩形, 梯形ACED
△ACB △BED △ABD 2 2 2
∴四边形 ABCE的面积为 ∴ BF DE 1.5m ,DF BE , a b a b = 1 ab+ 1 1AB 7.5 m , AE 15.5 m , 所以 ab c
2 .
∵
S 1 1 1 1 2 2 2 2△ABC S△AEC AB BC AC AE 12 16 20 15 96 150 2462 2 2 2 ∴ BC AB 7.5 ,DF BE AE AB 15.5 7.5 8 , a2 b2 = 1 2 2 2 2
平方米 ∴CF BC BF 7.5 1.5 6 ,
整理,得 c ,即a b c ;
2 2
(2)由(1)可得△ACE是直角三角形, CAE 90 在Rt△ABC中, AB2 BC2 AC2 , (2)因为BD x,所以CD BC BD 6 x .
依题意,ED DC EA AC 15 20 35米, AC 15∴ 2 , 在Rt△ABD中,由勾股定理,得 AD
2 AB2 BD2 16 x2 ,
设DE x米,则CD 35 x 米 2 在Rt△ACD中,由勾股定理,得
2 2 2
在Rt△ACD中,CD2 AC 2 AD2 在Rt△CDF 中,CD CF DF , AD2 AC2 CD2 25 6 x 2,
35 ∴CD 10 ,∴ x 2 202 15 x 2 215 所以16 x2 25 6 x ,
解得: x 6 ,即线段DE的长度为 6 米. 绳长为 AC CD 2 10;2 9
17.答案:(1)见解析 解得 x ;(2)由题意得DF BE 12 , 4
(2)20
在Rt△CDF 中,CD2 CF 2 DF 2 , (3)在解决以上问题的过程中,让我们感悟的数学思想有①方程
解析:(1)证明:连接 AE,CF,
设CD x , BC x 6.5 , 思想,②数形结合思想,
∵ BF 1.5 , 故答案为:①②.
∴CF BC BF x 6.5 1.5 x 8 , 21.答案:(1)BF 5 1
即 x2 x 8 2 122 , (2) AE DE BF .理由见解析
解得: x 13 , (3)当点 E与点 C重合时,AE最大为2 2 ,面积和最大值为
BC x 6.5 13 6.5 6.5 , 2 2
∴ AB BC 6.5; 22.答案:(1) 2 5
ABCD , 19.答案:(1)10 13m∵四边形 是平行四边形 (2)当0 t 2时,PB 2 t;当2 t 4时, PB 5 t 2
∴ AD//BC , (2)2000 元 14
∴ OAF OCE , 解析: (1)长方形 ABCD的周长为2 AB BC (3)t的值为 2 或 5
在△AOF和△COE中, 2 2 13 3 13 (4) t 1 7或
OAF COE 2
2 5 13
AO CO ,
10 13 m ,
AOF COE
答:长方形 ABCD的周长为10 13m .
∴△AOF≌△COE ASA
(2) 2 13 3 13 4 2 2 4 2 2
∴FO EO ,
又∵ AO CO , 78 32 4
∴四边形 AECF是平行四边形, 78 28
∴ AF EC; 50 m2 ,
(2) AC 8 ,EF 6 .
∴OA OC 4 ,OE OF 40 50 2000(元), 3 ,
∵EF AC , 答:定期维护的总费用为 2000 元.
AECF , 20.答案:(1)见解析;∴四边形 是菱形
∴ AE EC CF FA 42 32 5 , (2) x
9
;
4
3
数学试卷 7.若代数式 在实数范围内有意义,则 x的取值范围为___________.x 1
1. 120 120 8.在矩形 ABCD中,E为边 AD的中点,F为边 BC上的一点,连接 EF ,DF ,若 AB 4 ,BC 8 ,EF 5 ,则本试卷为数学科目,考试形式为闭卷,全卷满分 分,考试时间 分钟,请合理安排答题时间。
2. DF ______.答题前,请务必将自己的姓名、班级、考号等信息准确填写在答题卡和试卷相应位置。
3.选择题答案须用 2B铅笔规范填涂在答题卡上,非选择题请用黑色字迹的钢笔或签字笔作答,答案必须写在 9.如图,在矩形 ABCD中, AB 3 , BC 2 ,M是 AD边的中点,N是 AB边上的动点,将△AMN沿 MN所在
答题卡指定区域内,写在试卷上无效。 直线折叠,得到△A MN ,连接 A C ,则 A C的最小值是______.
4.闭卷考试不允许查阅教材及相关资料,请独立思考、诚信作答,禁止交流讨论、传递资料等作弊行为。
5.答题时请注意字迹工整、卷面整洁,合理组织语言,条理清晰地表达观点。
6.考试结束后,请将试卷和答题卡一并交回,不得带出考场。
一、单选题(每题 3 分,共 18分)
1.下列二次根式中,与 2是同类二次根式的是( ) 第九题图 第十题图 第十一题图
A. 4 B. 6 C. 8 D. 12 10.如图, ABCD的周长为 36,对角线 AC,BD相交于点 O.点 E是 CD的中点, BD 12 ,则△DOE的周长
2.勾股数,又名毕达哥拉斯三元数,是指可以构成一个直角三角形三边的一组正整数.下列各组数中 为______.
是勾股数的是( ) 11.我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由
A.0.6,0.8,1 B.1,3,10 C.5,10,12 D.3,4,5 商高发现,故又称之为“商高定理”.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼
3.矩形具有而平行四边形不一定具有的性质是( ) 成的一个大正方形,若大正方形的面积是 25,小正方形的面积是 1,直角三角形的两条直角边长分别为
A.对边相等 B.对角相等 m、n,则mn ______.
C.对角线相等 D.对角线互相平分
4.如图,在矩形 ABCD中,对角线 AC , BD相关于点 O,E为边CD上的任意一点(不与点 C,D重合),过点 E 三、解答题(12—14每题6分,15—17每题7分,18—19每题8分,20—21每题10分,22题12分,共87分)
作 EF BD , EG AC ,垂足分别为 F,G,若 AB 8 ,BC 6 ,则EF EG的值为( )
12.(6分)已知: x 1 2 , y 1 2 ,求 x2 y2 xy 2x 2y 的值.
A. 24 B.12 C.5 D.6
5 5
5.a、b 2 2、c为△ABC三边,不是直角三角形的是( ) 13.(6分)已知 a 2 5,b 2 5 ,求代数式 a b ab 的值.
A.a2 c2 b2 B. a 5 3 ,b 1, c
4 4
C. A : B : C 3 : 4 : 5 D. a 8k ,b 17k , c 15k
6.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形 ABCD和 EFGH .连接EG , BD相交于点
O, BD S与HC相交于点 P.若GO GP ,则 △ABD 的值是( )
S△EFG
a 1 a2 1
14.(6分)先化简,再求值: 2 a ,其中a 1 2 .a 2a 1 a 1
A.1 2 B. 2 2 C.5 2 D.15
4
第 1页 共 4页
15.(7分)如图,正方形网格中的每个小正方形的边长都是 1,每个小格的顶点叫做格点. 17.(7分)如图,在 ABCD中,点 E,F分别在BC , AD上, AC与 EF 交于点 O,且 AO CO .
(1)在图(1)中以格点为顶点画一个面积为 10的正方形;
(2)在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为 2, 5, 13 . (1)求证: AF EC;
(2)连接 AE ,CF ,若 AC 8 ,EF 6 ,且EF AC ,求四边形 AECF的周长.
16.(7分)如图,某居民小区有一块四边形空地 ABCD ,小道 AC和CE把这块空地分成了△ABC、 18.(8分)古代护城河上有座吊桥,图 1是它的结构原理图,图 2是它的示意图.把桥面看成是均匀杆
△ACE和△CDE三个区域,分别摆放三种不同的花卉.已知 B 90 , AB 12米,BC 16米, AE 15 AB ,可以绕转轴 B点在竖直平面内转动,在 B点正上方固定一个定滑轮 C,绳子通过定滑轮与杆的另一
米,CE 25米. 端 A相连,且 AB BC .某人站在点 E处,拉绳子的手的位置 D与地面 E的距离为1.5m .
(1)求四边形 ABCE的面积;
(2)小明和小林同时以相同的速度同时从点 E出发,分别沿E A C和E D C两条不同的路径散
步,结果两人同时到达点 C,求线段DE的长度.
(1)若 AB 7.5 m , AE 15.5 m ,求从 A到定滑轮 C,再到 D点拉着的绳长(结果保留根号);
(2)若BE的长为12 m ,CD比 BC长6.5m ,求桥面的宽 AB .
第 2页 共 4页
19.(8分)怀仁市为做好城市园林绿化工作,进一步改善城市生态环境,美化城市居住环境,提升 20.(10 分)综合与实践
人民群众获得感、幸福感、对市内绿地进行改建.如图,该市某公园有一块长方形绿地 ABCD, AB的长 【背景介绍】勾股定理是几何学中的明珠,充满着魅力.勾股定理是用代数思想解决几何问题的最重要
为2 13m,BC的长为3 13 m,绿地内有一块长方形花坛(图中阴影部分),长为 4 2 2 m,宽为 的工具之一,它不但因验证方法层出不穷吸引着人们,更因为应用广泛而使人着迷.
【验证方法】如图①是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以验证勾股定理.
4 2 2 m . 思路:大正方形的面积有两种求法,一种是等于 c2 .另一种是等于四个直角三角形与一个小正方形的面
1
积之和,即 ab 4 1 b a 2 2,从而得到等式c2 ab 4 b a .化简便得结论 a2 b2 c2 .
2 2
这种用两种求法表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
(1)求长方形 ABCD的周长;
(2)除花坛外的绿地(图中空白部分)另作他用,需要 40元 /m2的定期维护费,求定期维护的总费用.
(1)【方法应用】千百年来,人们对勾股定理的验证趋之若鹜,其中有著名的数学家,也有业余数学爱
好者.美国第 20任总统詹姆斯·伽菲尔德利用图②验证了勾股定理:把两个全等的直角三角形如图②所
示放置,请根据图形面积之间的关系,验证勾股定理a2 b2 c2 .
(2)【方法迁移】请利用“双求法”解决下面的问题:如图③,在△ABC中, AD是BC边上的高,
AB 4, AC 5,BC 6,设BD x,求 x的值.
(3)【数学思想】在解决以上问题的过程中,让我们感悟的数学思想有___________.(填序号)
①方程思想②数形结合思想③分类讨论思想
第 3页 共 4页
21.(10 分) 22.(12 分)如图,在△ABC中, A 90 , AB 2, AC 4,点 D为边 AC的中点.动点 P从点 A
如图,已知正方形 ABCD的边长为 2,点 E是边 CD上的一动点,AF平分 BAE交边 BC于点 F. 出发,沿折线 AB BC向点 C运动,点 P在 AB上以每秒 1个单位长度的速度运动,在BC上以每秒
5个单位长度的速度运动.在点 P运动过程中,连接 PD,将△APD沿 PD翻折得到△A PD .设点 P的
运动时间为 t秒 0 t 4 .
(1)①当点 F恰好是边 BC的中点时,求线段 DE长;
②当点 E恰好是边 CD的中点时,求线段 BF长. (1)BC的长为______.
(2)猜想线段 AE,DE,BF之间的数量关系,并说明理由. (2)用含 t的代数式表示线段BP的长.
(3)直接写△ADE与△ABF面积和的最大值. (3)当四边形 APA D为中心对称图形时,求 t的值.
(4)连结 AA ,当 AA D与 B相等时,直换写出 t的值.
第 4页 共 4页
达里巴中学·八年级数学 又∵ DBC 45 , 故答案为: 65 或 17 .
∴ GBC 22.5 ,
参考答案 9.答案: 10 1∴ PBG GBC , 10.答案:15
1.答案:C ∵ BGP BGC 90 ,BG BG , 11.答案:12
2.答案:D ∴△BPG≌△BCG(ASA) , 解析:∵大正方形的面积是 25,
3.答案:C ∴PG CG . ∴m2 n2 25 ,
4.答案:A 设OG PG CG x , ∵小正方形的面积是 1,
解析:连接OE ,如图: ∵O为 EG,BD的交点,
∴ m n 2 1,
∴EG 2x ,FG 2x ,
∴m2 2mn n2 1 ,
∵四个全等的直角三角形拼成“赵爽弦图”,
∴BF CG x , ∴25 2mn 1 ,
∴2mn 24 ,
∴BG x 2x ,
∴mn 12 ,
∴BC 2 BG2 CG2 x2 ( 2 1)2 x2 (4 2 2)x2 , 故答案为:12.
∵四边形 ABCD是矩形, S△ABD S= 正方形ABCD (4 2 2)x
2
∴ 12.答案:7 4 22 2 2 .
∴ ABC 90 ,OA OC ,OB OD , AC BD , S△EFG S正方形EFGH 2x 解析:∵ x 1 2 , y 1 2 ,
∴OD OC , AC AB2 BC2 62 82 10 , 故选:B. ∴ x y (1 2) (1 2) 2 2
7.答案: x 1
∴ S ABCD AB·BC
1
48 , S△DOC S ,OD OC 5 ,
xy (1 2)(1 2) 1
矩形 4 矩形ABCD
12 8.答案: 65 或 17
∴ x2 y2 xy 2x 2y
∴ 解析:①如图所示,当BF CF时,过 F作FG AD于 G,则 2
S S S 1OD·EF 1
GF AB 4 , x y 2 x y xy
△DOC △DOE △COE OC·EG
1
OD FE 1 EG 5 EF EG 12
2 2 2 2 ( 2 2)2 2 ( 2 2) ( 1)
, 7 4 2 .
∴ EF 24 EG ; 13.答案:-4
5 解析: a2b ab2 ab(a b)
故选:A.
C (2 5)(2 5)(2 5 2 5)5.答案:
解析:A、∵a2 c2 b2 ,∴a2 b2 c2 ,∴a、b、c为△ABC三边, 在Rt△EFG中,EG 52 42 3 ,
1 4 4.
E AD , AD BC 8 , 故代数式的值为-4是直角三角形,故本选项错误; 又∵ 是 的中点
2 2 2 1 2B、∵b c a ,∴a、b、c 为△ABC三边,是直角三角形,故本 ∴DE 4 , 14.答案: , 1
∴DG 4 3 1, a 1 2选项错误;
15.答案:(1)详见解析;(2)详见解析.
C、∵ A : B : C 3 : 4 : 5 ,∴设 A 3x ,则 B 4x , C 5x , ∴Rt△DFG中,DF 42 12 17 ; (1)如图 1 所示:正方形 ABCD 即为所求;
∵ A B C 180 ,即3x 4x 5x 180 ,解得, x 15 , ②如图所示,当BF CF时,过 F作FG AD于 G,则GF AB 4 , (2)如图 2 所示:三角形 ABC 即为所求.
∴5x 5 15 75 90 ,∴a、b、c为△ABC三边,不是直角三
角形,故本选项正确;
D、∵a2 c2 b2 ,∴a、b、c为△ABC三边,是直角三角形,故本
选项错误.
故选:C.
6.答案:B
解析:∵四边形 EFGH 2为正方形, 在Rt△EFG中,EG 5 4 3 ,
∴ EGH 45 , FGH 90 , 又∵E是 AD的中点, AD BC 8 ,
∵OG GP , ∴DE 4 ,
∴ GOP OPG 67.5 , ∴DG 4 3 7 ,
∴ PBG 22.5 , ∴Rt△DFG中,中,DF 42 72 65 , 16.答案:(1) 246平方米
(2)线段DE的长度为 6 米 C
菱形AECF 20; (3)①②
解析:(1)∵ B 90 , AB 12米, BC 16米 15 a b(1) a b 18.答案:(1) 2 10 解析: 证明:观察图形可知 S
AC AB2 BC2 20 2 梯形ACED
或
∴ 米 2
∵ AC 2 AE 2 202 152 625 252 CE 2 (2) 6.5 S 1 S S S ab+ 1 ab 1 c2 .
∴△ACE是直角三角形,且 CAE 90 解析:(1)依题意得:DFBE是矩形, 梯形ACED
△ACB △BED △ABD 2 2 2
∴四边形 ABCE的面积为 ∴ BF DE 1.5m ,DF BE , a b a b = 1 ab+ 1 1AB 7.5 m , AE 15.5 m , 所以 ab c
2 .
∵
S 1 1 1 1 2 2 2 2△ABC S△AEC AB BC AC AE 12 16 20 15 96 150 2462 2 2 2 ∴ BC AB 7.5 ,DF BE AE AB 15.5 7.5 8 , a2 b2 = 1 2 2 2 2
平方米 ∴CF BC BF 7.5 1.5 6 ,
整理,得 c ,即a b c ;
2 2
(2)由(1)可得△ACE是直角三角形, CAE 90 在Rt△ABC中, AB2 BC2 AC2 , (2)因为BD x,所以CD BC BD 6 x .
依题意,ED DC EA AC 15 20 35米, AC 15∴ 2 , 在Rt△ABD中,由勾股定理,得 AD
2 AB2 BD2 16 x2 ,
设DE x米,则CD 35 x 米 2 在Rt△ACD中,由勾股定理,得
2 2 2
在Rt△ACD中,CD2 AC 2 AD2 在Rt△CDF 中,CD CF DF , AD2 AC2 CD2 25 6 x 2,
35 ∴CD 10 ,∴ x 2 202 15 x 2 215 所以16 x2 25 6 x ,
解得: x 6 ,即线段DE的长度为 6 米. 绳长为 AC CD 2 10;2 9
17.答案:(1)见解析 解得 x ;(2)由题意得DF BE 12 , 4
(2)20
在Rt△CDF 中,CD2 CF 2 DF 2 , (3)在解决以上问题的过程中,让我们感悟的数学思想有①方程
解析:(1)证明:连接 AE,CF,
设CD x , BC x 6.5 , 思想,②数形结合思想,
∵ BF 1.5 , 故答案为:①②.
∴CF BC BF x 6.5 1.5 x 8 , 21.答案:(1)BF 5 1
即 x2 x 8 2 122 , (2) AE DE BF .理由见解析
解得: x 13 , (3)当点 E与点 C重合时,AE最大为2 2 ,面积和最大值为
BC x 6.5 13 6.5 6.5 , 2 2
∴ AB BC 6.5; 22.答案:(1) 2 5
ABCD , 19.答案:(1)10 13m∵四边形 是平行四边形 (2)当0 t 2时,PB 2 t;当2 t 4时, PB 5 t 2
∴ AD//BC , (2)2000 元 14
∴ OAF OCE , 解析: (1)长方形 ABCD的周长为2 AB BC (3)t的值为 2 或 5
在△AOF和△COE中, 2 2 13 3 13 (4) t 1 7或
OAF COE 2
2 5 13
AO CO ,
10 13 m ,
AOF COE
答:长方形 ABCD的周长为10 13m .
∴△AOF≌△COE ASA
(2) 2 13 3 13 4 2 2 4 2 2
∴FO EO ,
又∵ AO CO , 78 32 4
∴四边形 AECF是平行四边形, 78 28
∴ AF EC; 50 m2 ,
(2) AC 8 ,EF 6 .
∴OA OC 4 ,OE OF 40 50 2000(元), 3 ,
∵EF AC , 答:定期维护的总费用为 2000 元.
AECF , 20.答案:(1)见解析;∴四边形 是菱形
∴ AE EC CF FA 42 32 5 , (2) x
9
;
4
同课章节目录
