陕西省汉中市西乡县第一中学2024?2025学年高三下学期3月月考数学试题(含详解)
文档属性
| 名称 | 陕西省汉中市西乡县第一中学2024?2025学年高三下学期3月月考数学试题(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 866.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览




文档简介
陕西省汉中市西乡县第一中学2024 2025学年高三下学期3月月考数学试题
一、单选题(本大题共8小题)
1.设集合,,则( )
A. B. C. D.
2.设,则( )
A.1 B.2 C. D.
3.函数的单调递增区间是( )
A.
B.
C.
D.
4.已知两个非零向量,满足,则向量在向量上的投影向量为( )
A. B. C. D.
5.袋中有除颜色外完全相同的6个小球,其中4个白球和2个红球,现从袋中不放回地连取两个.在第一次取得白球前提下,则第二次取得红球的概率为( )
A.0.25 B.0.4 C.0.5 D.0.6
6.如图,测量河对岸的塔高时,可以选取与塔底在同一水平面内的两个测量基点与.现测得,,米,在点测得塔顶的仰角,则塔高约为( )(单位:米,)
A.42.42 B.45.42 C.50.42 D.60.42
7.如图,这是战国时楚国标准度量衡器,于1954年出土于湖南长沙的木衡铜环权,包括木质秤杆、两个铜盘和九枚铜环权,为等臂衡秤式样,其中铜环权类似于砝码,用于测量物体质量.已知九枚铜环权中质量最小的为1铢,最大的为8两(古制1两=24铢,1斤=16两),且按从小到大的顺序排列后前3项构成等差数列,后7项构成公比为2的等比数列,若某物体的质量恰为第2,5,7枚铜环权的质量和,则该物体的质量为( )
A.2两4铢 B.2两14铢 C.3两2铢 D.3两12铢
8.已知函数的定义域为,,都有:,且,则( )
A.1600 B.1601 C.820 D.821
二、多选题(本大题共3小题)
9.某手机商城统计的2024年5个月智能手机的销量(万部)如下表所示:根据表中数据用最小二乘法得到的关于月份编号的回归直线方程为,则( )
月份 7月 8月 9月 10月 11月
x 1 2 3 4 5
y 2 2 3 m 4
A.
B.与正相关
C.当月份编号增加1时,销量增加0.5万部
D.预测2025年6月份该手机商城的销量约为6万部
10.已知抛物线的焦点为为坐标原点,点在抛物线上,若,则( )
A.的坐标为 B.
C. D.
11.Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线,常被用作神经网络的激活函数.记为Sigmoid函数的导函数,则( )
A. B.Sigmoid函数是减函数
C.函数的最大值是 D.
三、填空题(本大题共3小题)
12.已知角的终边过点,则 .
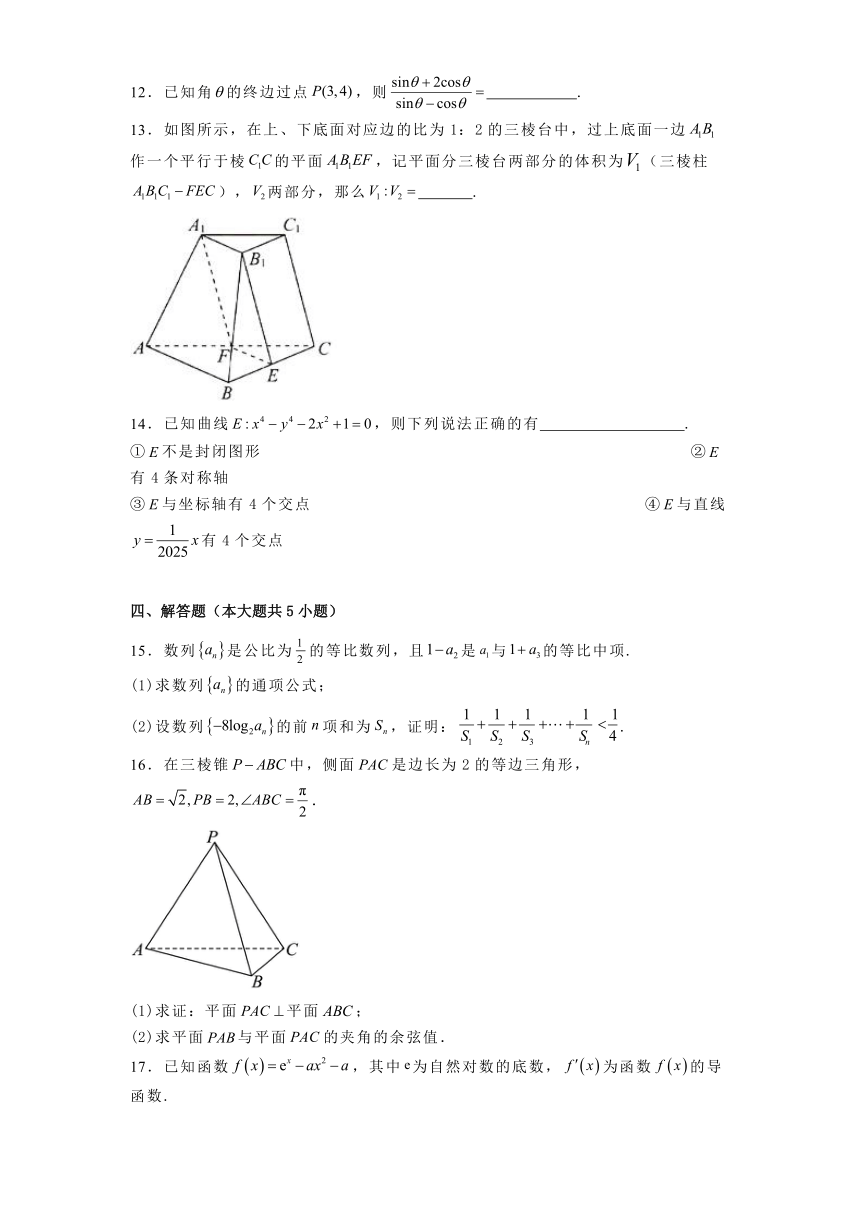
13.如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边作一个平行于棱的平面,记平面分三棱台两部分的体积为(三棱柱),两部分,那么 .
14.已知曲线,则下列说法正确的有 .
①不是封闭图形 ②有4条对称轴
③与坐标轴有4个交点 ④与直线有4个交点
四、解答题(本大题共5小题)
15.数列是公比为的等比数列,且是与的等比中项.
(1)求数列的通项公式;
(2)设数列的前项和为,证明:.
16.在三棱锥中,侧面是边长为2的等边三角形,.
(1)求证:平面平面;
(2)求平面与平面的夹角的余弦值.
17.已知函数,其中为自然对数的底数,为函数的导函数.
(1)当时,令,求在处的切线方程.
(2)若在区间上不是单调函数,求的取值范围.
(3)若方程有两个不等实根,求的取值范围.
18.某工厂为了提高精度,采购了一批新型机器,现对这批机器的生产效能进行测试,对其生产的第一批零件的直径进行测量,质检部门随机抽查了100个零件的进行统计整理,得到数据如下表:
零件直径(单位:厘米)
零件个数 10 25 30 25 10
已知零件的直径可视为服从正态分布,,分别为这100个零件的直径的平均数及方差(同一组区间的直径尺寸用该组区间的中点值代表).
参考数据:;若随机变量,则,
,.
(1)试估计这批零件直径在的概率;
(2)以频率估计概率,若在这批零件中随机抽取4个,记直径在区间内的零件个数为Z,求Z的分布列及数学期望;
(3)若此工厂有甲、乙两台机器生产这种零件,且甲机器的生产效率是乙机器的生产效率的3倍,甲机器生产的零件的次品率为0.3,乙机器生产的零件的次品率为0.2,现从这批零件中随机抽取一件.若检测出这个零件是次品,求这个零件是甲机器生产的概率.
19.已知平面上的动点到点的距离与到直线的距离相等,点的轨迹为曲线.
(1)求曲线的方程;
(2)设过点的直线交于两点,过点的直线与的另一个交点为,点在与之间.
(i)证明:线段垂直于轴;
(ii)记的面积为的面积为,求的取值范围.
参考答案
1.【答案】B
【详解】由集合,
又因为,可得.
故选B.
2.【答案】C
【详解】因为,所以,
所以,所以.
故选C.
3.【答案】C.
【详解】由,可得.
故选C.
4.【答案】D
【详解】因为,所以,
所以,所以向量在向量上的投影向量为.
故选D.
5.【答案】B
【详解】设第一次取得白球为事件,第二次取得红球为事件,
所以在第一次取得红球前提下,则第二次取得白球的概率为:
.
故选B.
6.【答案】A
【详解】由题意,在中,,
由正弦定理可知.
在中,易知,
于是.
故选A.
7.【答案】B
【详解】设九枚铜环权按从小到大的顺序排列后的质量为,
由题意知,,,得,
则,,,铢两14铢.
故选B.
8.【答案】D
【详解】依题意,由,得,两式相加得,
而,因此,
取,则,
所以
.
故选D.
9.【答案】AB
【详解】对于A,由表中数据,计算得,
故得到,
则,解得,故A正确,
对于B,由回归直线方程中的系数为正可知,
与正相关,且其相关系数,故B正确;
对于C,线性回归方程只是一种统计预测方法,当月份编号增加1时,销量不一定增加0.5万部,故C错误,
对于D,2025年6月份对应的月份编号,
而,故D错误.
故选AB.
10.【答案】BD
【详解】由抛物线,可得,所以,且焦点在y轴正半轴上,
则焦点,所以A错误;
由抛物线的定义,可得,解得,所以B正确;
由,可得,所以,则,所以C不正确;
由,所以D正确.
故选BD.
11.【答案】ACD
【分析】根据题意,求出导函数,代入验证可以判断A;利用导数研究函数的单调性,进而可以判断B;利用基本不等式,可以判断C;易知函数关于点对称,进而可以求D.
【详解】由函数得.
对于A,,故A正确;
对于B, ,,则Sigmoid函数是增函数,故B错误;
对于C,,当且仅当,即时取等号,故C正确;
对于D,因为++1,
所以,故D正确.
故选ACD.
【思路导引】求解函数的最值,导数法是一种很重要的方法,但在某些问题中,用导数可能很繁琐,可变形函数借助均值不等式、配方法等求解.
12.【答案】10
【详解】由角的终边过点,得,
所以.
13.【答案】3:4
【解析】设三棱台的高为,上底面的面积是,则下底面的面积是,计算体积得到答案.
【详解】设三棱台的高为,上底面的面积是,则下底面的面积是,
,.
14.【答案】①③④
【详解】对于①,因为,
所以或,
所以E是由单位圆M和实轴长为2,焦点为的等轴双曲线构成,故①正确;
对于②,由①项分析知,E只关于轴,轴对称,所以E只有两条对称轴,故②错误;
对于③,由①项分析可知,曲线E与坐标轴的交点为,故③正确;
对于④,因为C的一条渐近线方程为且,
根据双曲线的性质可知,直线与双曲线有2个交点,
又直线与圆M有2个交点,故直线与有4个交点,故④正确.
15.【答案】(1)
(2)证明见解析
【详解】(1)依题可得:,
即:,
解得,
所以.
(2)证明:设,
则,
所以,
16.【答案】(1)证明见解析
(2)
【详解】(1)取的中点为,连接,
因为是边长为2的等边三角形,所以,
在直角三角形中,,为中点,所以,
又,所以,
所以°,即,
又∵,,平面,
所以平面,
又平面,
所以平面平面.
(2)
由(1)知两两垂直,以为坐标原点建立如图所示空间直角坐标系
则,所以,
设平面的法向量为,
则,即,
令,可得,
设平面的法向量为,则,
设平面与平面的夹角为,
则,
所以平面与平面的夹角的余弦值为.
17.【答案】(1)
(2)
(3)
【详解】(1)当时,,所以,,,所以,所以在处的切线方程为;
(2)由,得,
记,所以,
当时,恒成立,为增函数,不符合题意,
当时,令,得,令,得,
所以在上单调递减,在上单调递增,
即在上单调递减,在上单调递增,
因为在区间上不是单调函数,所以,解得,
即的取值范围为.
(3)方程,
当时,显然方程不成立,所以,则.
方程有两个不等实根,即与的图象有个交点,
且,其中,
当或时,,在区间和上单调递减,
当时,,在区间上单调递增.
当时,,当时,,
则当时,且当时,取得极小值,
作出函数的图象,如图所示:
因此与有个交点时,,即,
故的取值范围为.
18.【答案】(1)0.47725;
(2)分布列见详解,1;
(3).
【详解】(1)由平均数与方差的计算公式分别得
,
,
故,,
设表示零件直径,则,即,
则,
,即;
(2)由题意知,这批零件直径在的概率为,
Z的取值范围为,
则,
,
,
,
,
因此可得Z的分布列为
Z 0 1 2 3 4
P
因为Z服从二项分布,则Z的数学期望;
(3)设“抽取的零件为甲机器生产”记为事件,“抽取的零件为乙机器生产”记为事件,
“抽取的零件为次品”记为事件B,
则,,,,
则,
,
所以这个零件是甲机器生产的概率为.
19.【答案】(1)
(2)(i)证明见解析;(ii).
【详解】(1)设点,由于动点到点的距离与直线的距离相等,
所以点的轨迹是以为焦点,为准线的抛物线.
设此抛物线的方程是,则,故曲线的方程是.
(2)(i)因为直线的斜率不为0,故设的方程为,
联立可得:,,
则,
.
故,故直线与直线关于轴对称,即点与点关于轴对称,所以线段垂直于轴.
(ii)由(i)可知,不妨设,因为点在与之间,所以,
,
则,
令,则,
令,则,解得;
令,解得.
则在上单调递增,在上单调递减,
,所以的取值范围为.
一、单选题(本大题共8小题)
1.设集合,,则( )
A. B. C. D.
2.设,则( )
A.1 B.2 C. D.
3.函数的单调递增区间是( )
A.
B.
C.
D.
4.已知两个非零向量,满足,则向量在向量上的投影向量为( )
A. B. C. D.
5.袋中有除颜色外完全相同的6个小球,其中4个白球和2个红球,现从袋中不放回地连取两个.在第一次取得白球前提下,则第二次取得红球的概率为( )
A.0.25 B.0.4 C.0.5 D.0.6
6.如图,测量河对岸的塔高时,可以选取与塔底在同一水平面内的两个测量基点与.现测得,,米,在点测得塔顶的仰角,则塔高约为( )(单位:米,)
A.42.42 B.45.42 C.50.42 D.60.42
7.如图,这是战国时楚国标准度量衡器,于1954年出土于湖南长沙的木衡铜环权,包括木质秤杆、两个铜盘和九枚铜环权,为等臂衡秤式样,其中铜环权类似于砝码,用于测量物体质量.已知九枚铜环权中质量最小的为1铢,最大的为8两(古制1两=24铢,1斤=16两),且按从小到大的顺序排列后前3项构成等差数列,后7项构成公比为2的等比数列,若某物体的质量恰为第2,5,7枚铜环权的质量和,则该物体的质量为( )
A.2两4铢 B.2两14铢 C.3两2铢 D.3两12铢
8.已知函数的定义域为,,都有:,且,则( )
A.1600 B.1601 C.820 D.821
二、多选题(本大题共3小题)
9.某手机商城统计的2024年5个月智能手机的销量(万部)如下表所示:根据表中数据用最小二乘法得到的关于月份编号的回归直线方程为,则( )
月份 7月 8月 9月 10月 11月
x 1 2 3 4 5
y 2 2 3 m 4
A.
B.与正相关
C.当月份编号增加1时,销量增加0.5万部
D.预测2025年6月份该手机商城的销量约为6万部
10.已知抛物线的焦点为为坐标原点,点在抛物线上,若,则( )
A.的坐标为 B.
C. D.
11.Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线,常被用作神经网络的激活函数.记为Sigmoid函数的导函数,则( )
A. B.Sigmoid函数是减函数
C.函数的最大值是 D.
三、填空题(本大题共3小题)
12.已知角的终边过点,则 .
13.如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边作一个平行于棱的平面,记平面分三棱台两部分的体积为(三棱柱),两部分,那么 .
14.已知曲线,则下列说法正确的有 .
①不是封闭图形 ②有4条对称轴
③与坐标轴有4个交点 ④与直线有4个交点
四、解答题(本大题共5小题)
15.数列是公比为的等比数列,且是与的等比中项.
(1)求数列的通项公式;
(2)设数列的前项和为,证明:.
16.在三棱锥中,侧面是边长为2的等边三角形,.
(1)求证:平面平面;
(2)求平面与平面的夹角的余弦值.
17.已知函数,其中为自然对数的底数,为函数的导函数.
(1)当时,令,求在处的切线方程.
(2)若在区间上不是单调函数,求的取值范围.
(3)若方程有两个不等实根,求的取值范围.
18.某工厂为了提高精度,采购了一批新型机器,现对这批机器的生产效能进行测试,对其生产的第一批零件的直径进行测量,质检部门随机抽查了100个零件的进行统计整理,得到数据如下表:
零件直径(单位:厘米)
零件个数 10 25 30 25 10
已知零件的直径可视为服从正态分布,,分别为这100个零件的直径的平均数及方差(同一组区间的直径尺寸用该组区间的中点值代表).
参考数据:;若随机变量,则,
,.
(1)试估计这批零件直径在的概率;
(2)以频率估计概率,若在这批零件中随机抽取4个,记直径在区间内的零件个数为Z,求Z的分布列及数学期望;
(3)若此工厂有甲、乙两台机器生产这种零件,且甲机器的生产效率是乙机器的生产效率的3倍,甲机器生产的零件的次品率为0.3,乙机器生产的零件的次品率为0.2,现从这批零件中随机抽取一件.若检测出这个零件是次品,求这个零件是甲机器生产的概率.
19.已知平面上的动点到点的距离与到直线的距离相等,点的轨迹为曲线.
(1)求曲线的方程;
(2)设过点的直线交于两点,过点的直线与的另一个交点为,点在与之间.
(i)证明:线段垂直于轴;
(ii)记的面积为的面积为,求的取值范围.
参考答案
1.【答案】B
【详解】由集合,
又因为,可得.
故选B.
2.【答案】C
【详解】因为,所以,
所以,所以.
故选C.
3.【答案】C.
【详解】由,可得.
故选C.
4.【答案】D
【详解】因为,所以,
所以,所以向量在向量上的投影向量为.
故选D.
5.【答案】B
【详解】设第一次取得白球为事件,第二次取得红球为事件,
所以在第一次取得红球前提下,则第二次取得白球的概率为:
.
故选B.
6.【答案】A
【详解】由题意,在中,,
由正弦定理可知.
在中,易知,
于是.
故选A.
7.【答案】B
【详解】设九枚铜环权按从小到大的顺序排列后的质量为,
由题意知,,,得,
则,,,铢两14铢.
故选B.
8.【答案】D
【详解】依题意,由,得,两式相加得,
而,因此,
取,则,
所以
.
故选D.
9.【答案】AB
【详解】对于A,由表中数据,计算得,
故得到,
则,解得,故A正确,
对于B,由回归直线方程中的系数为正可知,
与正相关,且其相关系数,故B正确;
对于C,线性回归方程只是一种统计预测方法,当月份编号增加1时,销量不一定增加0.5万部,故C错误,
对于D,2025年6月份对应的月份编号,
而,故D错误.
故选AB.
10.【答案】BD
【详解】由抛物线,可得,所以,且焦点在y轴正半轴上,
则焦点,所以A错误;
由抛物线的定义,可得,解得,所以B正确;
由,可得,所以,则,所以C不正确;
由,所以D正确.
故选BD.
11.【答案】ACD
【分析】根据题意,求出导函数,代入验证可以判断A;利用导数研究函数的单调性,进而可以判断B;利用基本不等式,可以判断C;易知函数关于点对称,进而可以求D.
【详解】由函数得.
对于A,,故A正确;
对于B, ,,则Sigmoid函数是增函数,故B错误;
对于C,,当且仅当,即时取等号,故C正确;
对于D,因为++1,
所以,故D正确.
故选ACD.
【思路导引】求解函数的最值,导数法是一种很重要的方法,但在某些问题中,用导数可能很繁琐,可变形函数借助均值不等式、配方法等求解.
12.【答案】10
【详解】由角的终边过点,得,
所以.
13.【答案】3:4
【解析】设三棱台的高为,上底面的面积是,则下底面的面积是,计算体积得到答案.
【详解】设三棱台的高为,上底面的面积是,则下底面的面积是,
,.
14.【答案】①③④
【详解】对于①,因为,
所以或,
所以E是由单位圆M和实轴长为2,焦点为的等轴双曲线构成,故①正确;
对于②,由①项分析知,E只关于轴,轴对称,所以E只有两条对称轴,故②错误;
对于③,由①项分析可知,曲线E与坐标轴的交点为,故③正确;
对于④,因为C的一条渐近线方程为且,
根据双曲线的性质可知,直线与双曲线有2个交点,
又直线与圆M有2个交点,故直线与有4个交点,故④正确.
15.【答案】(1)
(2)证明见解析
【详解】(1)依题可得:,
即:,
解得,
所以.
(2)证明:设,
则,
所以,
16.【答案】(1)证明见解析
(2)
【详解】(1)取的中点为,连接,
因为是边长为2的等边三角形,所以,
在直角三角形中,,为中点,所以,
又,所以,
所以°,即,
又∵,,平面,
所以平面,
又平面,
所以平面平面.
(2)
由(1)知两两垂直,以为坐标原点建立如图所示空间直角坐标系
则,所以,
设平面的法向量为,
则,即,
令,可得,
设平面的法向量为,则,
设平面与平面的夹角为,
则,
所以平面与平面的夹角的余弦值为.
17.【答案】(1)
(2)
(3)
【详解】(1)当时,,所以,,,所以,所以在处的切线方程为;
(2)由,得,
记,所以,
当时,恒成立,为增函数,不符合题意,
当时,令,得,令,得,
所以在上单调递减,在上单调递增,
即在上单调递减,在上单调递增,
因为在区间上不是单调函数,所以,解得,
即的取值范围为.
(3)方程,
当时,显然方程不成立,所以,则.
方程有两个不等实根,即与的图象有个交点,
且,其中,
当或时,,在区间和上单调递减,
当时,,在区间上单调递增.
当时,,当时,,
则当时,且当时,取得极小值,
作出函数的图象,如图所示:
因此与有个交点时,,即,
故的取值范围为.
18.【答案】(1)0.47725;
(2)分布列见详解,1;
(3).
【详解】(1)由平均数与方差的计算公式分别得
,
,
故,,
设表示零件直径,则,即,
则,
,即;
(2)由题意知,这批零件直径在的概率为,
Z的取值范围为,
则,
,
,
,
,
因此可得Z的分布列为
Z 0 1 2 3 4
P
因为Z服从二项分布,则Z的数学期望;
(3)设“抽取的零件为甲机器生产”记为事件,“抽取的零件为乙机器生产”记为事件,
“抽取的零件为次品”记为事件B,
则,,,,
则,
,
所以这个零件是甲机器生产的概率为.
19.【答案】(1)
(2)(i)证明见解析;(ii).
【详解】(1)设点,由于动点到点的距离与直线的距离相等,
所以点的轨迹是以为焦点,为准线的抛物线.
设此抛物线的方程是,则,故曲线的方程是.
(2)(i)因为直线的斜率不为0,故设的方程为,
联立可得:,,
则,
.
故,故直线与直线关于轴对称,即点与点关于轴对称,所以线段垂直于轴.
(ii)由(i)可知,不妨设,因为点在与之间,所以,
,
则,
令,则,
令,则,解得;
令,解得.
则在上单调递增,在上单调递减,
,所以的取值范围为.
同课章节目录
