重庆市万州第三中学224?2025学年高二下学期第一次月考 数学试题(含详解)
文档属性
| 名称 | 重庆市万州第三中学224?2025学年高二下学期第一次月考 数学试题(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 892.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览





文档简介
重庆市万州第三中学224 2025学年高二下学期第一次月考数学试题
一、单选题(本大题共8小题)
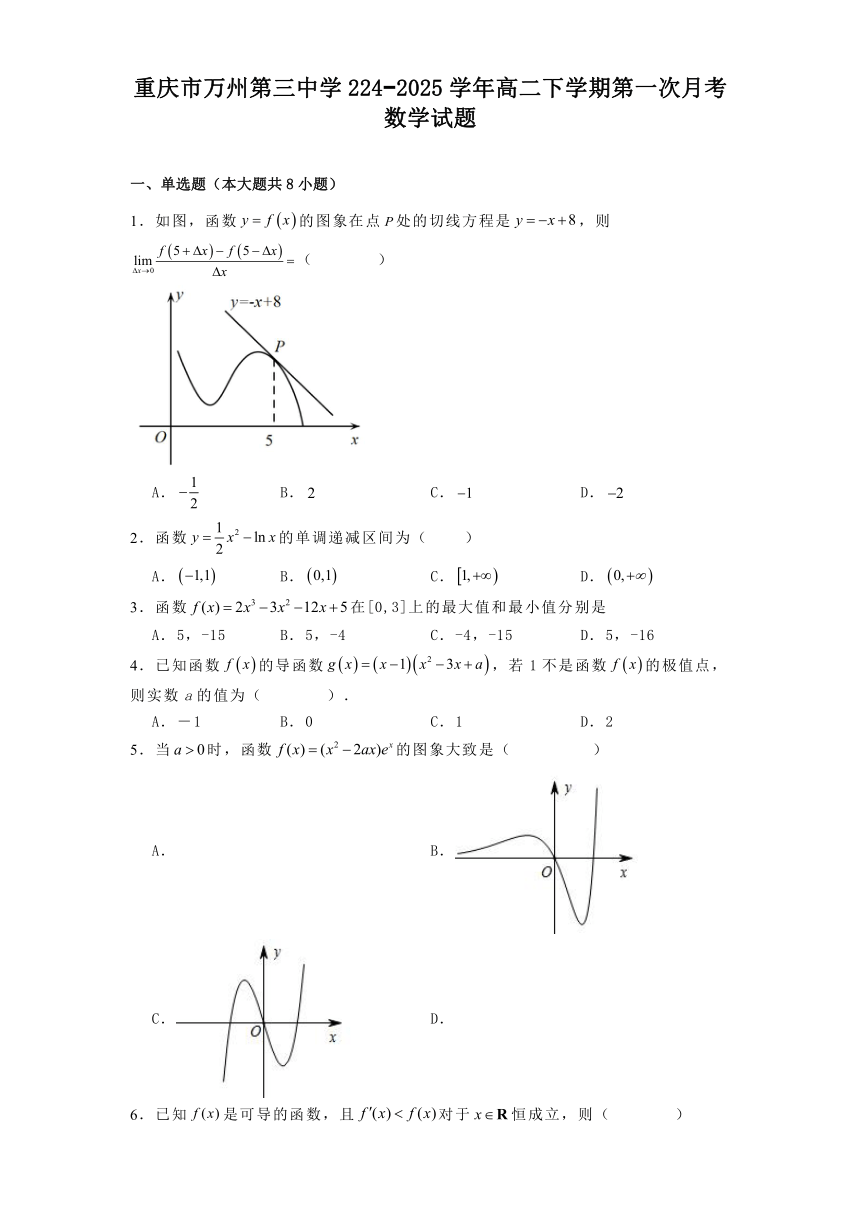
1.如图,函数的图象在点处的切线方程是,则( )
A. B. C. D.
2.函数的单调递减区间为( )
A. B. C. D.
3.函数在[0,3]上的最大值和最小值分别是
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
4.已知函数的导函数,若1不是函数的极值点,则实数a的值为( ).
A.-1 B.0 C.1 D.2
5.当时,函数的图象大致是( )
A. B.
C. D.
6.已知是可导的函数,且对于恒成立,则( )
A. B.
C. D.
7.若直线与曲线相切,则的取值范围为( )
A. B.
C. D.
8.已知函数,若对,都有,则实数的取值范围是( )
A. B. C. D.
二、多选题(本大题共3小题)
9.下列结论正确的是( )
A.
B.设函数,且,则
C.若,则
D.若,则
10.设函数定义域为,若函数满足:对任意,存在,使得成立,则称函数满足性质.下列函数满足性质的有( )
A. B. C. D.
11.已知函数的定义域为,其导函数为,且满足,,则下列结论一定成立的是( )
A.方程有唯一实数根
B.在区间上单调递增
C.
D.若且,则
三、填空题(本大题共3小题)
12.函数的极大值点是 ;
13.函数在上单调递增,则实数的取值范围为 ;
14.设是函数的导数,是函数的导数,若方程有实数解,则称点为函数的拐点.某同学经过探究发现:任何一个三次函数都有拐点,任何一个三次函数都有对称中心,且拐点就是对称中心,设函数,利用上述探究结果计算: ;
四、解答题(本大题共5小题)
15.已知函数在处取得极值.
(1)求函数的解析式;
(2)求曲线在点处的切线方程;
16.已知函数.
(1)讨论函数的单调性;
(2)当时,记函数的最小值为,求证:.
17.万州区为提高市民的健康水平,拟在半径为20米的半圆形区域内修建一个健身广场,该健身广场(如图所示的阴影部分)分休闲健身和儿童活动两个功能区,图中矩形区域是休闲健身区,以为底边的等腰三角形区域是儿童活动区,,,三点在圆弧上,中点恰好在圆心.设,健身广场的面积为.
(1)求出关于的函数解析式;
(2)当角取何值时,健身广场的面积最大?其最大面积是多少?
18.设函数
(1)当时,若在存在,使得不等式成立,求的最小值.
(2)若存在且,使得,求实数的取值范围.
(参考数据)
19.已知函数.
(1)当时,求的极值;
(2)若有两个极值点.
(i)求的取值范围;
(ii)证明:.
参考答案
1.【答案】D
【详解】依题意可知切点,
函数的图象在点处的切线方程是,
,即
又
即
故选D.
2.【答案】B
【详解】由题意,
在中,,
当时,解得(舍)或,
当即时,函数单调递减,
∴的单调递减区间为.
故选B.
3.【答案】A
【详解】,令,得或,所以当时,,即为单调递减函数,当时,,即为单调递增函数,所以,又,所以,故选A.
4.【答案】D
【详解】由题意可知,若1不是函数的极值点,则,即,
当时,,故当 ,当,因此是 的极值点,1不是极值点,故满足题意,
故选D.
5.【答案】B
【详解】根据f(x)<0 x2-2ax<0 00可知方程必存在两个根.设小的根为x0,则f(x)在(-∞,x0)上必定是单调递增的,故选B.
6.【答案】A
【详解】设,,则,
可得在上单调递减,
所以,即,
所以.
故选A.
7.【答案】C
【详解】设切点为,因为,所以.
又因为切点在直线上,
所以,解得,所以.
令,则,
所以在区间上,单调递减,
在区间上单调递增,
所以,故的取值范围为.
故选C.
8.【答案】B
【详解】函数,,,
令,显然函数在上单调递增,而不等式为,
因此,,
令函数,求导得,
当时,,单调递增,
当时,,单调递减,
因此,于是,解得,
所以实数的取值范围是.
故选B.
9.【答案】BD
【详解】对于A,由复合函数的导数公式得
,故A错误,
对于B,因为,所以,
令,得到,解得,故B正确,
对于C,因为,所以,故C错误,
对于D,因为,所以,
令,则,解得,故D正确.
故选BD.
10.【答案】ACD
【详解】可化为,
令,
则,令
则,
若在定义域内正负号不变,那么是的变号零点,
则在的两侧的单调性不一致,因此满足性质;
若有唯一变号零点,那么取,则在定义域内的正负号不变,
进而函数在定义域内单调,因此不满足性质.
对于A,,则,所以满足性质;
对于B,,则有唯一变号零点0,所以不满足性质;
对于C,,则,所以满足性质;
对于D,,则,所以满足性质.
故选ACD.
11.【答案】BCD
【详解】设,则,所以恒为常数.
又由于,故.
所以,即.
对于A,由于,故对有,对有.
从而在上递减,在上递增,故,所以方程没有实数根,故A错误;
对于B,前面已经证明在上递增,故B正确;
对于C,前面已经证明,所以,故C正确;
对于D,若,,则,
故D正确.
故选BCD.
12.【答案】
【详解】由题意得定义域为,
因为,所以,
令,,令,,
故在上单调递增,在上单调递减,
则函数的极大值点是.
13.【答案】
【详解】由,可得,.
因为函数在上单调递增,所以在上恒成立,
即在上恒成立,可得在上恒成立.
即在上恒成立.
设,则,
故在上单调递减.
所以在上的最大值为.
则.
同时,要使有意义,则在上恒成立,即在上恒成立,所以.
综上可得.
14.【答案】
【详解】因为,所以,.
由.
又,所以点是函数的拐点,也就是函数的对称中心.
所以,
所以,,…,,,
所以.
15.【答案】(1)
(2)
【详解】(1),
因为函数在处取得极值,
所以可得①,
②,
由①②解得,或,
所以,或
当时,
,
所以在R上单调递增,没有极值,不符合题意;
当时,,
当,或时,,当时,,
所以在,上都是单调递增,在单调递减,
所以在处取得极大值,且,符合题意.
综上;
(2)由(1),,
,切点坐标为,
切线斜率为,
所以曲线在点处的切线方程为,
即.
16.【答案】(1)答案见解析
(2)证明见解析.
【详解】(1)的定义域为,
,
当时,令,得,令,得,
所以在上单调递减,在上单调递增.
当时,令,得,令,得,
所以在上单调递减,在上单调递增.
(2)当时,由(1)知,在上单调递减,在上单调递增,
所以,
,
令,得,令,得,
所以在上单调递增,在上单调递减,
所以.
17.【答案】(1)
(2);
【详解】(1)由已知得,
等腰底边上的高为,
而,
,
,得到.
(2)设,则,
令,由,可得,令,可得,
故在上单调递增,在上单调递减,
则时,有,
故,即时,健康广场的面积最大,最大值为.
18.【答案】(1)
(2)
【详解】(1)若存在,使得不等式成立,则只需,
由题意得,当时,,
则,
当时,,函数单调递减;
当时,,函数单调递增;
当时,,函数单调递减,
故在处取得极小值,即,
又,而,
,因为,所以,
构造,由对数函数性质得在上单调递增,
则,即,得到,
故,即,得到,
则,即,得到.
(2)因为,所以,
因为存在且,使得,
所以在上不单调,下面我们对的范围分类讨论,
当时,,此时在上单调递增,与题意不符,排除,
当时,令,,
当时,得到,解得,
但此时,即,得到在上单调递减,与题意不符,排除,
当时,得到,解得,
此时结合二次函数性质得有两个变号零点,设其为,
即一元二次方程由两个根,且设,
由韦达定理得,,
故成立,得到有两个恒正的变号零点,
则有两个恒正的变号零点,满足,
令,,令,,
则在上单调递减,在上单调递增,
满足在上不单调,故符合题意.
19.【答案】(1)极大值为,极小值为.
(2)(i);(ii)证明过程见解析.
【详解】(1)当时, ,
则,
由得,;得,或,
则在和上单调递减,在上单调递增,
则的极大值为,极小值为.
(2)(i),
则,
令,则,
因,故,
当,即时,,
则在上单调递减,无极值,不满足题意;
当时,令,
欲使有两个极值点,
需使在上有两个不同零点,
则,即,
则的取值范围为.
(ii)由(i)可知,,
则
令,则,
令,则,
则在上单调递减,因,
则存在使得,即,
则当时,,在上单调递增;
当时,,在上单调递减,
则,
又,则,则.
一、单选题(本大题共8小题)
1.如图,函数的图象在点处的切线方程是,则( )
A. B. C. D.
2.函数的单调递减区间为( )
A. B. C. D.
3.函数在[0,3]上的最大值和最小值分别是
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
4.已知函数的导函数,若1不是函数的极值点,则实数a的值为( ).
A.-1 B.0 C.1 D.2
5.当时,函数的图象大致是( )
A. B.
C. D.
6.已知是可导的函数,且对于恒成立,则( )
A. B.
C. D.
7.若直线与曲线相切,则的取值范围为( )
A. B.
C. D.
8.已知函数,若对,都有,则实数的取值范围是( )
A. B. C. D.
二、多选题(本大题共3小题)
9.下列结论正确的是( )
A.
B.设函数,且,则
C.若,则
D.若,则
10.设函数定义域为,若函数满足:对任意,存在,使得成立,则称函数满足性质.下列函数满足性质的有( )
A. B. C. D.
11.已知函数的定义域为,其导函数为,且满足,,则下列结论一定成立的是( )
A.方程有唯一实数根
B.在区间上单调递增
C.
D.若且,则
三、填空题(本大题共3小题)
12.函数的极大值点是 ;
13.函数在上单调递增,则实数的取值范围为 ;
14.设是函数的导数,是函数的导数,若方程有实数解,则称点为函数的拐点.某同学经过探究发现:任何一个三次函数都有拐点,任何一个三次函数都有对称中心,且拐点就是对称中心,设函数,利用上述探究结果计算: ;
四、解答题(本大题共5小题)
15.已知函数在处取得极值.
(1)求函数的解析式;
(2)求曲线在点处的切线方程;
16.已知函数.
(1)讨论函数的单调性;
(2)当时,记函数的最小值为,求证:.
17.万州区为提高市民的健康水平,拟在半径为20米的半圆形区域内修建一个健身广场,该健身广场(如图所示的阴影部分)分休闲健身和儿童活动两个功能区,图中矩形区域是休闲健身区,以为底边的等腰三角形区域是儿童活动区,,,三点在圆弧上,中点恰好在圆心.设,健身广场的面积为.
(1)求出关于的函数解析式;
(2)当角取何值时,健身广场的面积最大?其最大面积是多少?
18.设函数
(1)当时,若在存在,使得不等式成立,求的最小值.
(2)若存在且,使得,求实数的取值范围.
(参考数据)
19.已知函数.
(1)当时,求的极值;
(2)若有两个极值点.
(i)求的取值范围;
(ii)证明:.
参考答案
1.【答案】D
【详解】依题意可知切点,
函数的图象在点处的切线方程是,
,即
又
即
故选D.
2.【答案】B
【详解】由题意,
在中,,
当时,解得(舍)或,
当即时,函数单调递减,
∴的单调递减区间为.
故选B.
3.【答案】A
【详解】,令,得或,所以当时,,即为单调递减函数,当时,,即为单调递增函数,所以,又,所以,故选A.
4.【答案】D
【详解】由题意可知,若1不是函数的极值点,则,即,
当时,,故当 ,当,因此是 的极值点,1不是极值点,故满足题意,
故选D.
5.【答案】B
【详解】根据f(x)<0 x2-2ax<0 0
6.【答案】A
【详解】设,,则,
可得在上单调递减,
所以,即,
所以.
故选A.
7.【答案】C
【详解】设切点为,因为,所以.
又因为切点在直线上,
所以,解得,所以.
令,则,
所以在区间上,单调递减,
在区间上单调递增,
所以,故的取值范围为.
故选C.
8.【答案】B
【详解】函数,,,
令,显然函数在上单调递增,而不等式为,
因此,,
令函数,求导得,
当时,,单调递增,
当时,,单调递减,
因此,于是,解得,
所以实数的取值范围是.
故选B.
9.【答案】BD
【详解】对于A,由复合函数的导数公式得
,故A错误,
对于B,因为,所以,
令,得到,解得,故B正确,
对于C,因为,所以,故C错误,
对于D,因为,所以,
令,则,解得,故D正确.
故选BD.
10.【答案】ACD
【详解】可化为,
令,
则,令
则,
若在定义域内正负号不变,那么是的变号零点,
则在的两侧的单调性不一致,因此满足性质;
若有唯一变号零点,那么取,则在定义域内的正负号不变,
进而函数在定义域内单调,因此不满足性质.
对于A,,则,所以满足性质;
对于B,,则有唯一变号零点0,所以不满足性质;
对于C,,则,所以满足性质;
对于D,,则,所以满足性质.
故选ACD.
11.【答案】BCD
【详解】设,则,所以恒为常数.
又由于,故.
所以,即.
对于A,由于,故对有,对有.
从而在上递减,在上递增,故,所以方程没有实数根,故A错误;
对于B,前面已经证明在上递增,故B正确;
对于C,前面已经证明,所以,故C正确;
对于D,若,,则,
故D正确.
故选BCD.
12.【答案】
【详解】由题意得定义域为,
因为,所以,
令,,令,,
故在上单调递增,在上单调递减,
则函数的极大值点是.
13.【答案】
【详解】由,可得,.
因为函数在上单调递增,所以在上恒成立,
即在上恒成立,可得在上恒成立.
即在上恒成立.
设,则,
故在上单调递减.
所以在上的最大值为.
则.
同时,要使有意义,则在上恒成立,即在上恒成立,所以.
综上可得.
14.【答案】
【详解】因为,所以,.
由.
又,所以点是函数的拐点,也就是函数的对称中心.
所以,
所以,,…,,,
所以.
15.【答案】(1)
(2)
【详解】(1),
因为函数在处取得极值,
所以可得①,
②,
由①②解得,或,
所以,或
当时,
,
所以在R上单调递增,没有极值,不符合题意;
当时,,
当,或时,,当时,,
所以在,上都是单调递增,在单调递减,
所以在处取得极大值,且,符合题意.
综上;
(2)由(1),,
,切点坐标为,
切线斜率为,
所以曲线在点处的切线方程为,
即.
16.【答案】(1)答案见解析
(2)证明见解析.
【详解】(1)的定义域为,
,
当时,令,得,令,得,
所以在上单调递减,在上单调递增.
当时,令,得,令,得,
所以在上单调递减,在上单调递增.
(2)当时,由(1)知,在上单调递减,在上单调递增,
所以,
,
令,得,令,得,
所以在上单调递增,在上单调递减,
所以.
17.【答案】(1)
(2);
【详解】(1)由已知得,
等腰底边上的高为,
而,
,
,得到.
(2)设,则,
令,由,可得,令,可得,
故在上单调递增,在上单调递减,
则时,有,
故,即时,健康广场的面积最大,最大值为.
18.【答案】(1)
(2)
【详解】(1)若存在,使得不等式成立,则只需,
由题意得,当时,,
则,
当时,,函数单调递减;
当时,,函数单调递增;
当时,,函数单调递减,
故在处取得极小值,即,
又,而,
,因为,所以,
构造,由对数函数性质得在上单调递增,
则,即,得到,
故,即,得到,
则,即,得到.
(2)因为,所以,
因为存在且,使得,
所以在上不单调,下面我们对的范围分类讨论,
当时,,此时在上单调递增,与题意不符,排除,
当时,令,,
当时,得到,解得,
但此时,即,得到在上单调递减,与题意不符,排除,
当时,得到,解得,
此时结合二次函数性质得有两个变号零点,设其为,
即一元二次方程由两个根,且设,
由韦达定理得,,
故成立,得到有两个恒正的变号零点,
则有两个恒正的变号零点,满足,
令,,令,,
则在上单调递减,在上单调递增,
满足在上不单调,故符合题意.
19.【答案】(1)极大值为,极小值为.
(2)(i);(ii)证明过程见解析.
【详解】(1)当时, ,
则,
由得,;得,或,
则在和上单调递减,在上单调递增,
则的极大值为,极小值为.
(2)(i),
则,
令,则,
因,故,
当,即时,,
则在上单调递减,无极值,不满足题意;
当时,令,
欲使有两个极值点,
需使在上有两个不同零点,
则,即,
则的取值范围为.
(ii)由(i)可知,,
则
令,则,
令,则,
则在上单调递减,因,
则存在使得,即,
则当时,,在上单调递增;
当时,,在上单调递减,
则,
又,则,则.
同课章节目录
