2025年九年级数学中考三轮冲刺训练圆中切线的判定与性质综合训练(二)(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练圆中切线的判定与性质综合训练(二)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 16:48:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练圆中切线的判定与性质综合训练(二)
1.如图,四边形ABCD内接于⊙O,AB=AD,连接BD,过A点作AE∥BD交CD的延长线于E.
(1)求证:AE为⊙O的切线;
(2)若AB∥CD,AB=8,CD=6,求⊙O半径的长.
2.如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求BC的长.
3.如图,菱形ABCD,AB=4,以AB为直径作⊙O,交AC于点E,过点E作EF⊥AD于点F.
(1)求证:EF是⊙O的切线;
(2)连接OF,若∠BAD=60°,求OF的长.
4.如图,在△ABC中,AB=BC,以BC为直径作⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若BG=OB,AC=6,求BF的长.
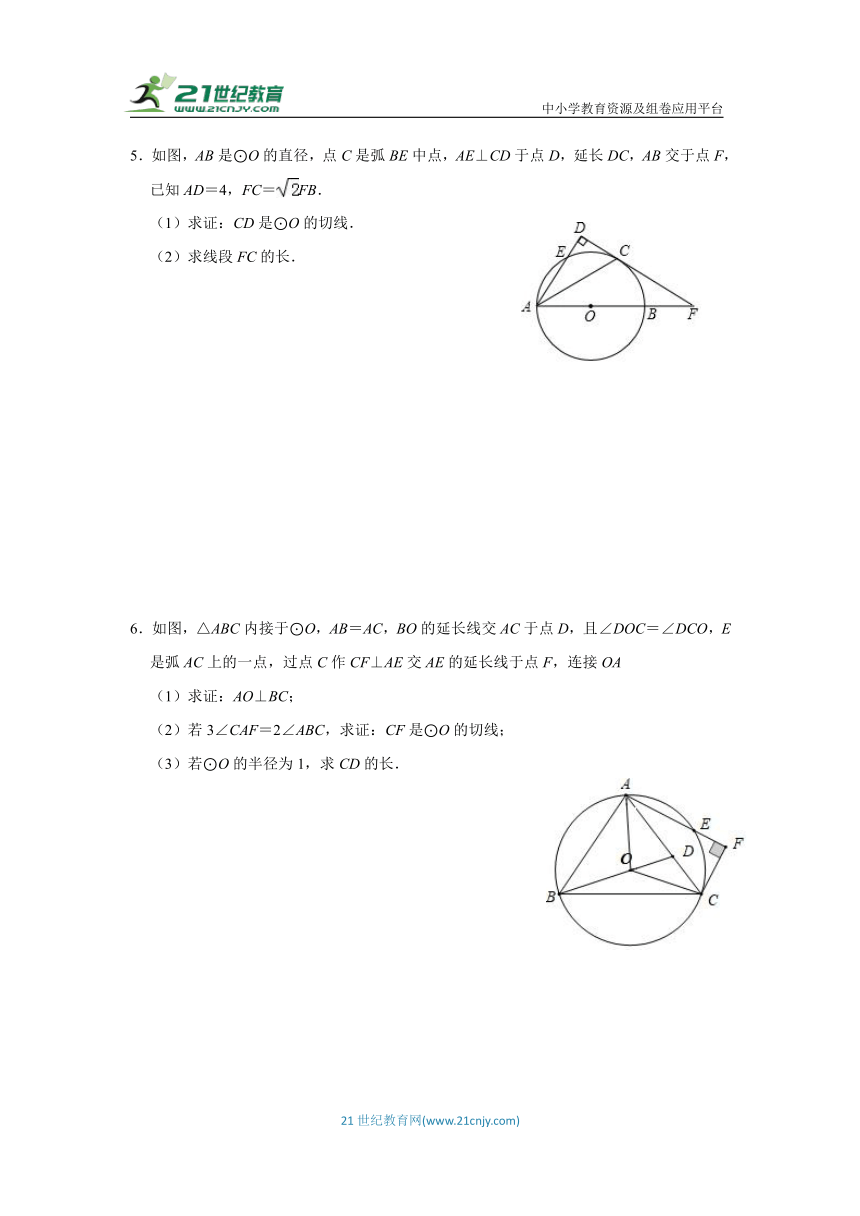
5.如图,AB是⊙O的直径,点C是弧BE中点,AE⊥CD于点D,延长DC,AB交于点F,已知AD=4,FC=FB.
(1)求证:CD是⊙O的切线.
(2)求线段FC的长.
6.如图,△ABC内接于⊙O,AB=AC,BO的延长线交AC于点D,且∠DOC=∠DCO,E是弧AC上的一点,过点C作CF⊥AE交AE的延长线于点F,连接OA
(1)求证:AO⊥BC;
(2)若3∠CAF=2∠ABC,求证:CF是⊙O的切线;
(3)若⊙O的半径为1,求CD的长.
7.如图,点A、B、C、D是⊙O上的四个点,AC是⊙O的直径,∠DAC=2∠BAC,过点B的直线与AC的延长线、DC的延长线分别相交于点E、F,且EF=CF.
(1)求证:BE是⊙O的切线;
(2)若⊙O的半径为5,CE=3,求CD的长.
8.如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
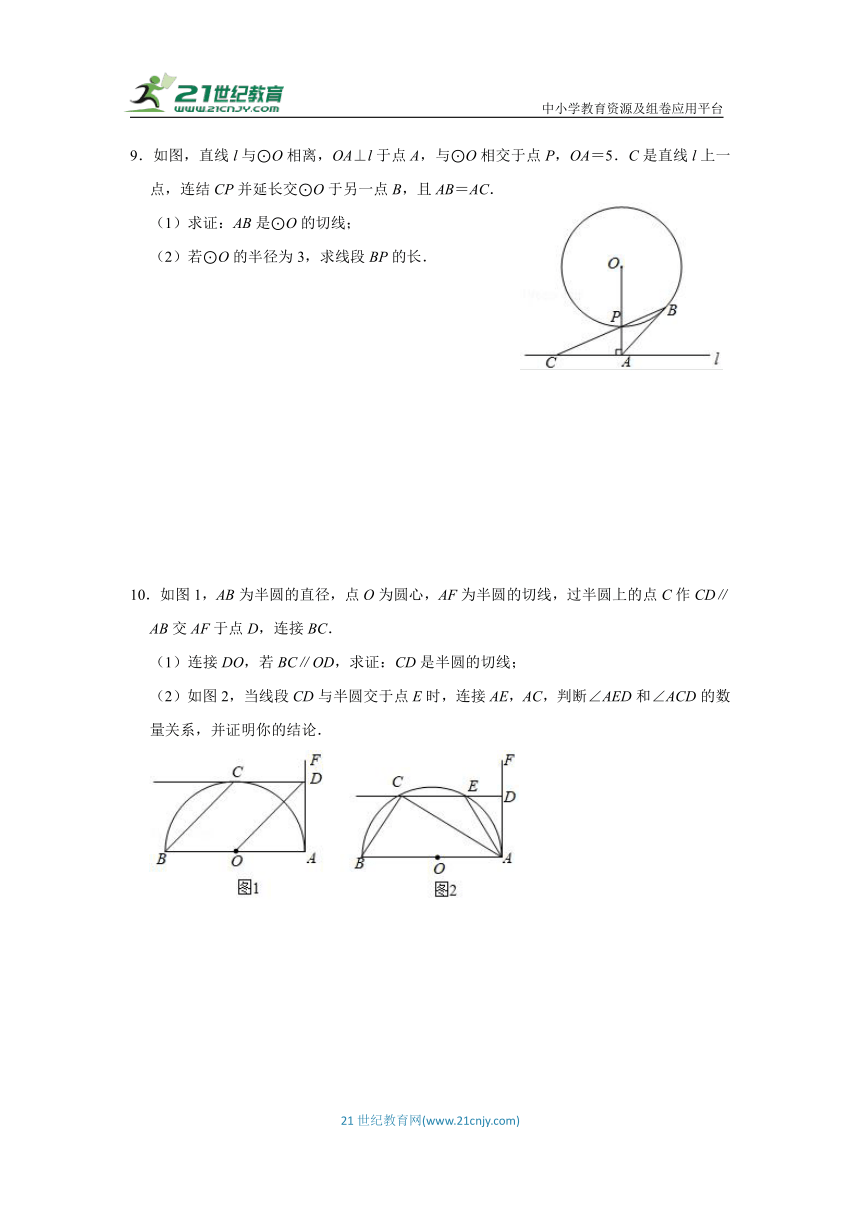
9.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连结CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
10.如图1,AB为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点C作CD∥AB交AF于点D,连接BC.
(1)连接DO,若BC∥OD,求证:CD是半圆的切线;
(2)如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论.
11.如图,点B是⊙O上一点,弦CD⊥OB于点E,过点C的切线交OB的延长线于点F,连接DF,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为2,∠CFD=60°,求CD的长.
12.如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上,⊙D经过点A和点B且与BC边相交于点E.
(1)求证:AC是⊙D的切线;
(2)若CE=2,求⊙D的半径.
13.如图,点D是以AB为直径的⊙O上一点,过点B作⊙O的切线,交AD的延长线于点C,E是BC的中点,连接DE并延长与AB的延长线交于点F.
(1)求证:DF是⊙O的切线;
(2)若OB=BF,EF=4,求AD的长.
14.如图,线段AB经过⊙O的圆心O,交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD,∠BAD=∠ABD=30°,连结DO并延长交⊙O于点E,连结BE交⊙O于点M.
(1)求证:直线BD是⊙O的切线;
(2)求⊙O的半径OD的长;
(3)求线段BM的长.
15.如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
16.如图,在△ABC中,E为BC边上一点,以BE为直径的AR半圆D与AC相切于点F,且EF∥AD,AD交半圆D于点G.
(1)求证:AB是半圆D的切线;
(2)若EF=2,AD=5,求切线长AB.
17.如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A.
(1)求证:BC是⊙O的切线;
(2)若BC=5,BD=3,求点O到CD的距离.
18.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=12,⊙O的半径为10,求CE的长.
19.如图,在△ABC中,AB=AC,点D是BC边上一点,且AD=BD,⊙O是△ACD的外接圆
(1)求证:直线AB是⊙O的切线;
(2)若AB=10,BC=16,求⊙O的半径.
20.如图,点O在△ABC的边BC上,⊙O经过点A、C,且与BC相交于点D,点E是下半圆的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O切线;
(2)若CF=4,EF=,求AB的长度.
参考答案
1.【解答】(1)证明:如图,连接OA,
∵AB=AD,
∴∠ABD=∠ADB,
∵AB=AD,OB=OD
∴∠BAO=∠DAO
∴∠OAD+∠ADB=90°
∵AE∥BD,
∴∠DAE=∠ADB,
∴∠OAD+∠EAD=90°,
即AE⊥OA,
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:如图,延长AO交BD于点F,连接OB,
∵AE∥BD,AB∥CD,
∴四边形ABDE为平行四边形,
∴AB=AD=DE=8,
∴∠BAO=∠ABO
∵AE为⊙O的切线,∴∠DAE+∠DAF=90°,
∵∠ADF+∠DAF=90°,
∴∠DAE=∠ADF,
∵∠ABD=∠ADF,
∴∠DAE=∠ABD=∠ACD,
∵∠E=∠E,
∴△ADE∽△CAE,
∴
∴AE2=DE CE,
∴,
∴AE=4,
∴,
∴,
∴=6,
由(1)知OA⊥BD,
∴在Rt△BOF中,OB2=OF2+BF2,
设OB=x,则OF=6﹣x,
∴,
解得:x=.
即⊙O的半径为.
2.【解答】解:(1)证明:连接OC,
∵AC是∠BAD的平分线,
∴∠CAD=∠BAC,
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
∴∠OCD=∠D=90°,
∴CD是⊙O的切线;
(2)解:∵∠ACD=60°,
∴∠OCA=30°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠OCB=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴OB=OC=BC=3,∠COB=60°,
∴的长:=π.
3.【解答】(1)证明:连接OE,
∵四边形ABCD是菱形,
∴∠CAD=∠CAB,
∵OA=OE,
∴∠OEA=∠CAB,
∴∠CAD=∠OEA,
∴OE∥AD,
∵EF⊥AD,
∴∠AFE=90°,
∴∠CAD+∠AEF=90°,
∴∠OEA+∠AEF=90°,即∠OEF=90°,
又∵OE是⊙O半径,
∴EF是⊙O的切线;
(2)解:连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°
∵∠BAD=60°,
∴∠CAD=∠CAB=30°,
在Rt△ABE中,,
在Rt△AEF中,,
在Rt△OEF中,OE═=2,
∴.
4.【解答】证明(1)如图:连接OE,BE
∵AB=BC,
∴∠C=∠A
∵BC是直径
∴∠CEB=90°,且AB=BC
∴CE=AE,且CO=OB
∴OE∥AB
∵GE⊥AB
∴EG⊥OE,且OE是半径
∴EG是⊙O的切线
(2)解:∵BG=OB,OE⊥EG,
∴BE=OG=OB=OC,
∴△OBE是等边三角形,
∴∠CBE=60°,
∵AC=6,
∴CE=3,BE==,
∴OE=,
∵OB=BG,OE∥AB,
∴BF=OE=.
5.【解答】(1)证明:连接OC.
∵C是的中点,
∴AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴DA∥OC,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCD=90°,
即OC⊥DC,
∵OC为半径,
∴DC为⊙O的切线;
(2)∵FC=FB,
∴设BF=x,则CF=x,
∵CD是⊙O的切线,
∴CF2=BF AF,
设OA=OC=OB=r,
∴2x2=x(x+2r),
∴x=2r,
∴BF=2r,
∵OC∥AD,
∴△OCF∽△ADF,
∴,
∴=,
∴r=3,
∴BF=6,
∴FC=FB=6.
6.【解答】(1)证明:
在△AOB和△AOC,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,
∴AO⊥BC;
(2)证明:∵AO=BO=CO,∠BAO=∠CAO,
∴∠ABO=∠BAO=∠CAO=∠ACO,∠OBC=∠OCB,
∵∠DOC=∠DCO,∠DOC=2∠OBC,
∴∠ABO=2∠OBC,
∴∠ABO=∠ABC,
∵3∠CAF=2∠ABC,
∴∠CAF=∠ABC,
∴∠CAF=∠ABO,
∴∠CAF=∠OCA,
∴AF∥OC,
∵CF⊥AF,
∴CF⊥OC;
(3)解:∵∠AOD=2∠BAO,∠ADO=2∠ACO,
∴∠AOD=∠ADO,
∴AD=AO=OC=1,
∵∠DOC=∠DCO=∠CAO,
∴△COD∽△CAO,
∴=,
∴OC2=CD AC,
设CD=x,则AC=x+1,
∴x(x+1)=1,
解得x1=,x2=,
∴CD=.
7.【解答】解:(1)连接OB.则∠BOC=2∠BAC.
∵∠DAC=2∠BAC,
∴∠BOC=∠DAC,
∵EF=CF,
∴∠FEC=∠FCE,
∵∠FCE=∠ACD,
∴∠FEC=∠ACD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∴∠BOC+∠ACD=90°,
∴∠OBE=180°﹣(∠BOE+∠FEC)=90°,
∴BE⊥OB,
∴BE是⊙O的切线;
(2)在Rt△OBE中,,
由(1)知,∠BOE=∠DAC,∠OBE=∠ADC,
∴△ADC∽△OBE,
∴,
即,
∴.
8.【解答】(1)证明:∵AE=AB,
∴△ABE是等腰三角形,
∵AB为⊙O的直径,
∴AF⊥BE,
∴EF=BF;
(2)证明:∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=(180°﹣∠BAC=)=90°﹣∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣∠BAC)+∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
(3)解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴,
∵在Rt△ABC中,AB=4,BC=3,
∴AC==5,
∴=,
解得:AD=3.2,
∵AE=AB=4,
∴DE=AE﹣AD=4﹣3.2=0.8.
9.【解答】(1)证明:如图,连结OB,则OP=OB,
∴∠OBP=∠OPB=∠CPA,
AB=AC,
∴∠ACB=∠ABC,
而OA⊥l,即∠OAC=90°,
∴∠ACB+∠CPA=90°,
即∠ABP+∠OBP=90°,
∴∠ABO=90°,
OB⊥AB,
故AB是⊙O的切线;
(2)解:由(1)知:∠ABO=90°,
而OA=5,OB=OP=3,
由勾股定理,得:AB=4,
过O作OD⊥PB于D,则PD=DB,
∵∠OPD=∠CPA,∠ODP=∠CAP=90°,
∴△ODP∽△CAP,
∴,
又∵AC=AB=4,AP=OA﹣OP=2,
∴,
∴,
∴.
10.【解答】(1)证明:连接OC,
∵AF为半圆的切线,AB为半圆的直径,
∴AB⊥AD,
∵CD∥AB,BC∥OD,
∴四边形BODC是平行四边形,
∴OB=CD,
∵OA=OB,
∴CD=OA,
∴四边形ADCO是平行四边形,
∴OC∥AD,
∵CD∥BA,
∴CD⊥AD,
∵OC∥AD,
∴OC⊥CD,
∴CD是半圆的切线;
(2)解:∠AED+∠ACD=90°,
理由:如图2,连接BE,
∵AB为半圆的直径,
∴∠AEB=90°,
∴∠EBA+∠BAE=90°,
∵∠DAE+∠BAE=90°,
∴∠ABE=∠DAE,
∵∠ACE=∠ABE,
∴∠ACE=∠DAE,
∵∠ADE=90°,
∴∠DAE+∠AED=∠AED+∠ACD=90°.
11.【解答】(1)证明:连接OD,如图,
∵CF是⊙O的切线
∴∠OCF=90°,
∴∠OCD+∠DCF=90°
∵直径AB⊥弦CD,
∴CE=ED,即OF为CD的垂直平分线
∴CF=DF,
∴∠CDF=∠DCF,
∵OC=OD,
∴∠CDO=∠OCD
∴∠CDO+∠CDB=∠OCD+∠DCF=90°,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:∵FC,FD是⊙O的切线,∠CFD=60°,
∴∠CFO=30°,
∴∠COF=60°,
∵CD⊥OB,
∴∠OCE=30°,
∵OC=2,
∴CE=OC=,
∴CD=2CE=2.
12.【解答】(1)证明:连接AD,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=60°,
∴∠DAC=180°﹣60°﹣30°=90°,
∴AC是⊙D的切线;
(2)解:连接AE,
∵AD=DE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=DE,∠AED=60°,
∴∠EAC=∠AED﹣∠C=30°,
∴∠EAC=∠C,
∴AE=CE=2,
∴⊙D的半径AD=2.
13.【解答】解:(1)如图,连接OD,BD,
∵AB为⊙O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,∵BE=EC,
∴DE=EC=BE,
∴∠1=∠3,
∵BC是⊙O的切线,
∴∠3+∠4=90°,
∴∠1+∠4=90°,
又∵∠2=∠4,
∴∠1+∠2=90°,
∴DF为⊙O的切线;
(2)∵OB=BF,
∴OF=2OD,
∴∠F=30°,
∵∠FBE=90°,
∴BE=EF=2,
∴DE=BE=2,
∴DF=6,
∵∠F=30°,∠ODF=90°,
∴∠FOD=60°,
∵OD=OA,
∴∠A=∠ADO=BOD=30°,
∴∠A=∠F,
∴AD=DF=6.
14.【解答】(1)证明:∵OA=OD,∠A=∠ABD=30°,
∴∠A=∠ADO=30°,
∴∠DOB=∠A+∠ADO=60°,
∴∠ODB=180°﹣∠DOB﹣∠B=90°,
∵OD是半径,
∴BD是⊙O的切线;
(2)∵∠ODB=90°,∠DBC=30°,
∴OD=OB,
∵OC=OD,
∴BC=OC=1,
∴⊙O的半径OD的长为1;
(3)∵OD=1,
∴DE=2,BD=,
∴BE==,
∵BD是⊙O的切线,BE是⊙O 的割线,
∴BD2=BM BE,
∴BM===.
15.【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
∵点F是ED的中点,
∴CF=EF=DF,
∴∠AEO=∠FEC=∠FCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OD⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠FCE=90°,即OC⊥FC,
∴CF与⊙O相切;
(2)解:连接AD,∵OD⊥AB,AC⊥BD,
∴∠AOE=∠ACD=90°,
∵∠AEO=∠DEC,
∴∠OAE=∠CDE=22.5°,
∵AO=BO,
∴AD=BD,
∴∠ADO=∠BDO=22.5°,
∴∠ADB=45°,
∴∠CAD=∠ADC=45°,
∴AC=CD.
16.【解答】(1)证明:连接DF,
∵AC与半圆D相切于点F,
∴DF⊥AC,
∴∠AFD=90°,
∵EF∥AD,
∴∠EFD=∠ADF,∠FED=∠ADB,
又∵DF=DE,
∴∠EFD=∠FED,
∴∠ADF=∠ADB,
在△ABD与△AFD中
∴△ABD≌△AFD (SAS),
∴∠ABD=∠AFD=90°,
∴AB是半圆D的切线;
(2)解:∵EF∥AD,
∴△CFE∽△CAD,
∴,
设CE=2x,
∴CD=5x,DF=DE=3x,
∴在Rt△DFC中,由勾股定理得CF=4x,
∴AF=6x,
在Rt△ADF中,(6x)2+(3x)2=52,
解得x=,
∴AB=AF=6x=2.
17.【解答】(1)证明:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∵∠BCD=∠A,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴BC是⊙O的切线;
(2)解:过O作OH⊥CD于H,
∵∠BDC=∠ACB=90°,∠B=∠B,
∴△ACB∽△CDB,
∴=,
∴=,
∴AB=,
∴AD=,
∵OH⊥CD,
∴CH=DH,
∵AO=OC,
∴OH=AD=,
∴点O到CD的距离是.
18.【解答】(1)证明:连接OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵OB=OE,
∴∠ABE=∠OEB,
∴∠CBE=∠OEB,
∴OE∥BC,
∵∠ACB=90°,
∴OE⊥AC,
∴AC是⊙O的切线;
(2)解:过O作OH⊥BC于H,
∴BH=HF=6,
在Rt△OBH中,
OH===8,
在矩形OHCE中,CE=OH=8.
19.【解答】(1)证明:连接AO并延长交⊙O于E,连接DE,
∵AB=AC,AD=BD,
∴∠B=∠BAD,∠B=∠C,
∴∠C=∠E,
∴∠E=∠BAD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠DAE=90°,
∴∠BAD+∠DAE=90°,
即∠BAE=90°,
∴直线AB是⊙O的切线;
(2)解:过A作AF⊥BC于F,
∵∠B=∠BAD,∠B=∠C,
∴∠BAD=∠C,
∵∠B=∠B,
∴△BAD∽△BCA,
∴,
∴BD==,
∴AD=BD=,
∵AB=AC,AF⊥BC,
∴BF=BC=8,
∴AF==6,
∵∠E=∠C=∠B,
∴sinE=sinB,
∴=,
∴AE=,
∴⊙O的半径为.
20.【解答】解:(1)连接AO、EO,
∵点E是下半圆的中点,
∴∠DOE=∠COE=90°,
∴∠OEF+∠EFO=90°,
∵∠EFO=∠BFA,
∴∠OEF+∠BFA=90°,
∵AB=BF,AO=EO,
∴∠BFA=∠BAF,∠OEF=∠OAF,
∴∠BAF+∠OAF=∠BFA+∠OEF=90°,
即∠BAO=90°,
∵A为⊙O上的一点,
∴AB是⊙O切线;
(2)设FO=x,则CO=FC﹣FO=4﹣x,
∴EO=CO=4﹣x,
在Rt△EFO中,EO2+FO2=EF2,
∴(4﹣x)2+x2=()2,
解得:x1=1,x2=3(不合题意,舍去),
∴AO=CO=4﹣1=3,
设AB=y,则BO=BF+FO=y+1,
在Rt△ABO中,AO2+AB2=BO2,
∴32+y2=(y+1)2,
解得:y=4,
∴AB=4.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练圆中切线的判定与性质综合训练(二)
1.如图,四边形ABCD内接于⊙O,AB=AD,连接BD,过A点作AE∥BD交CD的延长线于E.
(1)求证:AE为⊙O的切线;
(2)若AB∥CD,AB=8,CD=6,求⊙O半径的长.
2.如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求BC的长.
3.如图,菱形ABCD,AB=4,以AB为直径作⊙O,交AC于点E,过点E作EF⊥AD于点F.
(1)求证:EF是⊙O的切线;
(2)连接OF,若∠BAD=60°,求OF的长.
4.如图,在△ABC中,AB=BC,以BC为直径作⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若BG=OB,AC=6,求BF的长.
5.如图,AB是⊙O的直径,点C是弧BE中点,AE⊥CD于点D,延长DC,AB交于点F,已知AD=4,FC=FB.
(1)求证:CD是⊙O的切线.
(2)求线段FC的长.
6.如图,△ABC内接于⊙O,AB=AC,BO的延长线交AC于点D,且∠DOC=∠DCO,E是弧AC上的一点,过点C作CF⊥AE交AE的延长线于点F,连接OA
(1)求证:AO⊥BC;
(2)若3∠CAF=2∠ABC,求证:CF是⊙O的切线;
(3)若⊙O的半径为1,求CD的长.
7.如图,点A、B、C、D是⊙O上的四个点,AC是⊙O的直径,∠DAC=2∠BAC,过点B的直线与AC的延长线、DC的延长线分别相交于点E、F,且EF=CF.
(1)求证:BE是⊙O的切线;
(2)若⊙O的半径为5,CE=3,求CD的长.
8.如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
9.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连结CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
10.如图1,AB为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点C作CD∥AB交AF于点D,连接BC.
(1)连接DO,若BC∥OD,求证:CD是半圆的切线;
(2)如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论.
11.如图,点B是⊙O上一点,弦CD⊥OB于点E,过点C的切线交OB的延长线于点F,连接DF,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为2,∠CFD=60°,求CD的长.
12.如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上,⊙D经过点A和点B且与BC边相交于点E.
(1)求证:AC是⊙D的切线;
(2)若CE=2,求⊙D的半径.
13.如图,点D是以AB为直径的⊙O上一点,过点B作⊙O的切线,交AD的延长线于点C,E是BC的中点,连接DE并延长与AB的延长线交于点F.
(1)求证:DF是⊙O的切线;
(2)若OB=BF,EF=4,求AD的长.
14.如图,线段AB经过⊙O的圆心O,交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD,∠BAD=∠ABD=30°,连结DO并延长交⊙O于点E,连结BE交⊙O于点M.
(1)求证:直线BD是⊙O的切线;
(2)求⊙O的半径OD的长;
(3)求线段BM的长.
15.如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
16.如图,在△ABC中,E为BC边上一点,以BE为直径的AR半圆D与AC相切于点F,且EF∥AD,AD交半圆D于点G.
(1)求证:AB是半圆D的切线;
(2)若EF=2,AD=5,求切线长AB.
17.如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A.
(1)求证:BC是⊙O的切线;
(2)若BC=5,BD=3,求点O到CD的距离.
18.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=12,⊙O的半径为10,求CE的长.
19.如图,在△ABC中,AB=AC,点D是BC边上一点,且AD=BD,⊙O是△ACD的外接圆
(1)求证:直线AB是⊙O的切线;
(2)若AB=10,BC=16,求⊙O的半径.
20.如图,点O在△ABC的边BC上,⊙O经过点A、C,且与BC相交于点D,点E是下半圆的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O切线;
(2)若CF=4,EF=,求AB的长度.
参考答案
1.【解答】(1)证明:如图,连接OA,
∵AB=AD,
∴∠ABD=∠ADB,
∵AB=AD,OB=OD
∴∠BAO=∠DAO
∴∠OAD+∠ADB=90°
∵AE∥BD,
∴∠DAE=∠ADB,
∴∠OAD+∠EAD=90°,
即AE⊥OA,
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:如图,延长AO交BD于点F,连接OB,
∵AE∥BD,AB∥CD,
∴四边形ABDE为平行四边形,
∴AB=AD=DE=8,
∴∠BAO=∠ABO
∵AE为⊙O的切线,∴∠DAE+∠DAF=90°,
∵∠ADF+∠DAF=90°,
∴∠DAE=∠ADF,
∵∠ABD=∠ADF,
∴∠DAE=∠ABD=∠ACD,
∵∠E=∠E,
∴△ADE∽△CAE,
∴
∴AE2=DE CE,
∴,
∴AE=4,
∴,
∴,
∴=6,
由(1)知OA⊥BD,
∴在Rt△BOF中,OB2=OF2+BF2,
设OB=x,则OF=6﹣x,
∴,
解得:x=.
即⊙O的半径为.
2.【解答】解:(1)证明:连接OC,
∵AC是∠BAD的平分线,
∴∠CAD=∠BAC,
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
∴∠OCD=∠D=90°,
∴CD是⊙O的切线;
(2)解:∵∠ACD=60°,
∴∠OCA=30°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠OCB=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴OB=OC=BC=3,∠COB=60°,
∴的长:=π.
3.【解答】(1)证明:连接OE,
∵四边形ABCD是菱形,
∴∠CAD=∠CAB,
∵OA=OE,
∴∠OEA=∠CAB,
∴∠CAD=∠OEA,
∴OE∥AD,
∵EF⊥AD,
∴∠AFE=90°,
∴∠CAD+∠AEF=90°,
∴∠OEA+∠AEF=90°,即∠OEF=90°,
又∵OE是⊙O半径,
∴EF是⊙O的切线;
(2)解:连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°
∵∠BAD=60°,
∴∠CAD=∠CAB=30°,
在Rt△ABE中,,
在Rt△AEF中,,
在Rt△OEF中,OE═=2,
∴.
4.【解答】证明(1)如图:连接OE,BE
∵AB=BC,
∴∠C=∠A
∵BC是直径
∴∠CEB=90°,且AB=BC
∴CE=AE,且CO=OB
∴OE∥AB
∵GE⊥AB
∴EG⊥OE,且OE是半径
∴EG是⊙O的切线
(2)解:∵BG=OB,OE⊥EG,
∴BE=OG=OB=OC,
∴△OBE是等边三角形,
∴∠CBE=60°,
∵AC=6,
∴CE=3,BE==,
∴OE=,
∵OB=BG,OE∥AB,
∴BF=OE=.
5.【解答】(1)证明:连接OC.
∵C是的中点,
∴AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴DA∥OC,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCD=90°,
即OC⊥DC,
∵OC为半径,
∴DC为⊙O的切线;
(2)∵FC=FB,
∴设BF=x,则CF=x,
∵CD是⊙O的切线,
∴CF2=BF AF,
设OA=OC=OB=r,
∴2x2=x(x+2r),
∴x=2r,
∴BF=2r,
∵OC∥AD,
∴△OCF∽△ADF,
∴,
∴=,
∴r=3,
∴BF=6,
∴FC=FB=6.
6.【解答】(1)证明:
在△AOB和△AOC,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,
∴AO⊥BC;
(2)证明:∵AO=BO=CO,∠BAO=∠CAO,
∴∠ABO=∠BAO=∠CAO=∠ACO,∠OBC=∠OCB,
∵∠DOC=∠DCO,∠DOC=2∠OBC,
∴∠ABO=2∠OBC,
∴∠ABO=∠ABC,
∵3∠CAF=2∠ABC,
∴∠CAF=∠ABC,
∴∠CAF=∠ABO,
∴∠CAF=∠OCA,
∴AF∥OC,
∵CF⊥AF,
∴CF⊥OC;
(3)解:∵∠AOD=2∠BAO,∠ADO=2∠ACO,
∴∠AOD=∠ADO,
∴AD=AO=OC=1,
∵∠DOC=∠DCO=∠CAO,
∴△COD∽△CAO,
∴=,
∴OC2=CD AC,
设CD=x,则AC=x+1,
∴x(x+1)=1,
解得x1=,x2=,
∴CD=.
7.【解答】解:(1)连接OB.则∠BOC=2∠BAC.
∵∠DAC=2∠BAC,
∴∠BOC=∠DAC,
∵EF=CF,
∴∠FEC=∠FCE,
∵∠FCE=∠ACD,
∴∠FEC=∠ACD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∴∠BOC+∠ACD=90°,
∴∠OBE=180°﹣(∠BOE+∠FEC)=90°,
∴BE⊥OB,
∴BE是⊙O的切线;
(2)在Rt△OBE中,,
由(1)知,∠BOE=∠DAC,∠OBE=∠ADC,
∴△ADC∽△OBE,
∴,
即,
∴.
8.【解答】(1)证明:∵AE=AB,
∴△ABE是等腰三角形,
∵AB为⊙O的直径,
∴AF⊥BE,
∴EF=BF;
(2)证明:∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=(180°﹣∠BAC=)=90°﹣∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣∠BAC)+∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
(3)解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴,
∵在Rt△ABC中,AB=4,BC=3,
∴AC==5,
∴=,
解得:AD=3.2,
∵AE=AB=4,
∴DE=AE﹣AD=4﹣3.2=0.8.
9.【解答】(1)证明:如图,连结OB,则OP=OB,
∴∠OBP=∠OPB=∠CPA,
AB=AC,
∴∠ACB=∠ABC,
而OA⊥l,即∠OAC=90°,
∴∠ACB+∠CPA=90°,
即∠ABP+∠OBP=90°,
∴∠ABO=90°,
OB⊥AB,
故AB是⊙O的切线;
(2)解:由(1)知:∠ABO=90°,
而OA=5,OB=OP=3,
由勾股定理,得:AB=4,
过O作OD⊥PB于D,则PD=DB,
∵∠OPD=∠CPA,∠ODP=∠CAP=90°,
∴△ODP∽△CAP,
∴,
又∵AC=AB=4,AP=OA﹣OP=2,
∴,
∴,
∴.
10.【解答】(1)证明:连接OC,
∵AF为半圆的切线,AB为半圆的直径,
∴AB⊥AD,
∵CD∥AB,BC∥OD,
∴四边形BODC是平行四边形,
∴OB=CD,
∵OA=OB,
∴CD=OA,
∴四边形ADCO是平行四边形,
∴OC∥AD,
∵CD∥BA,
∴CD⊥AD,
∵OC∥AD,
∴OC⊥CD,
∴CD是半圆的切线;
(2)解:∠AED+∠ACD=90°,
理由:如图2,连接BE,
∵AB为半圆的直径,
∴∠AEB=90°,
∴∠EBA+∠BAE=90°,
∵∠DAE+∠BAE=90°,
∴∠ABE=∠DAE,
∵∠ACE=∠ABE,
∴∠ACE=∠DAE,
∵∠ADE=90°,
∴∠DAE+∠AED=∠AED+∠ACD=90°.
11.【解答】(1)证明:连接OD,如图,
∵CF是⊙O的切线
∴∠OCF=90°,
∴∠OCD+∠DCF=90°
∵直径AB⊥弦CD,
∴CE=ED,即OF为CD的垂直平分线
∴CF=DF,
∴∠CDF=∠DCF,
∵OC=OD,
∴∠CDO=∠OCD
∴∠CDO+∠CDB=∠OCD+∠DCF=90°,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:∵FC,FD是⊙O的切线,∠CFD=60°,
∴∠CFO=30°,
∴∠COF=60°,
∵CD⊥OB,
∴∠OCE=30°,
∵OC=2,
∴CE=OC=,
∴CD=2CE=2.
12.【解答】(1)证明:连接AD,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=60°,
∴∠DAC=180°﹣60°﹣30°=90°,
∴AC是⊙D的切线;
(2)解:连接AE,
∵AD=DE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=DE,∠AED=60°,
∴∠EAC=∠AED﹣∠C=30°,
∴∠EAC=∠C,
∴AE=CE=2,
∴⊙D的半径AD=2.
13.【解答】解:(1)如图,连接OD,BD,
∵AB为⊙O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,∵BE=EC,
∴DE=EC=BE,
∴∠1=∠3,
∵BC是⊙O的切线,
∴∠3+∠4=90°,
∴∠1+∠4=90°,
又∵∠2=∠4,
∴∠1+∠2=90°,
∴DF为⊙O的切线;
(2)∵OB=BF,
∴OF=2OD,
∴∠F=30°,
∵∠FBE=90°,
∴BE=EF=2,
∴DE=BE=2,
∴DF=6,
∵∠F=30°,∠ODF=90°,
∴∠FOD=60°,
∵OD=OA,
∴∠A=∠ADO=BOD=30°,
∴∠A=∠F,
∴AD=DF=6.
14.【解答】(1)证明:∵OA=OD,∠A=∠ABD=30°,
∴∠A=∠ADO=30°,
∴∠DOB=∠A+∠ADO=60°,
∴∠ODB=180°﹣∠DOB﹣∠B=90°,
∵OD是半径,
∴BD是⊙O的切线;
(2)∵∠ODB=90°,∠DBC=30°,
∴OD=OB,
∵OC=OD,
∴BC=OC=1,
∴⊙O的半径OD的长为1;
(3)∵OD=1,
∴DE=2,BD=,
∴BE==,
∵BD是⊙O的切线,BE是⊙O 的割线,
∴BD2=BM BE,
∴BM===.
15.【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
∵点F是ED的中点,
∴CF=EF=DF,
∴∠AEO=∠FEC=∠FCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OD⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠FCE=90°,即OC⊥FC,
∴CF与⊙O相切;
(2)解:连接AD,∵OD⊥AB,AC⊥BD,
∴∠AOE=∠ACD=90°,
∵∠AEO=∠DEC,
∴∠OAE=∠CDE=22.5°,
∵AO=BO,
∴AD=BD,
∴∠ADO=∠BDO=22.5°,
∴∠ADB=45°,
∴∠CAD=∠ADC=45°,
∴AC=CD.
16.【解答】(1)证明:连接DF,
∵AC与半圆D相切于点F,
∴DF⊥AC,
∴∠AFD=90°,
∵EF∥AD,
∴∠EFD=∠ADF,∠FED=∠ADB,
又∵DF=DE,
∴∠EFD=∠FED,
∴∠ADF=∠ADB,
在△ABD与△AFD中
∴△ABD≌△AFD (SAS),
∴∠ABD=∠AFD=90°,
∴AB是半圆D的切线;
(2)解:∵EF∥AD,
∴△CFE∽△CAD,
∴,
设CE=2x,
∴CD=5x,DF=DE=3x,
∴在Rt△DFC中,由勾股定理得CF=4x,
∴AF=6x,
在Rt△ADF中,(6x)2+(3x)2=52,
解得x=,
∴AB=AF=6x=2.
17.【解答】(1)证明:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∵∠BCD=∠A,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴BC是⊙O的切线;
(2)解:过O作OH⊥CD于H,
∵∠BDC=∠ACB=90°,∠B=∠B,
∴△ACB∽△CDB,
∴=,
∴=,
∴AB=,
∴AD=,
∵OH⊥CD,
∴CH=DH,
∵AO=OC,
∴OH=AD=,
∴点O到CD的距离是.
18.【解答】(1)证明:连接OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵OB=OE,
∴∠ABE=∠OEB,
∴∠CBE=∠OEB,
∴OE∥BC,
∵∠ACB=90°,
∴OE⊥AC,
∴AC是⊙O的切线;
(2)解:过O作OH⊥BC于H,
∴BH=HF=6,
在Rt△OBH中,
OH===8,
在矩形OHCE中,CE=OH=8.
19.【解答】(1)证明:连接AO并延长交⊙O于E,连接DE,
∵AB=AC,AD=BD,
∴∠B=∠BAD,∠B=∠C,
∴∠C=∠E,
∴∠E=∠BAD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠DAE=90°,
∴∠BAD+∠DAE=90°,
即∠BAE=90°,
∴直线AB是⊙O的切线;
(2)解:过A作AF⊥BC于F,
∵∠B=∠BAD,∠B=∠C,
∴∠BAD=∠C,
∵∠B=∠B,
∴△BAD∽△BCA,
∴,
∴BD==,
∴AD=BD=,
∵AB=AC,AF⊥BC,
∴BF=BC=8,
∴AF==6,
∵∠E=∠C=∠B,
∴sinE=sinB,
∴=,
∴AE=,
∴⊙O的半径为.
20.【解答】解:(1)连接AO、EO,
∵点E是下半圆的中点,
∴∠DOE=∠COE=90°,
∴∠OEF+∠EFO=90°,
∵∠EFO=∠BFA,
∴∠OEF+∠BFA=90°,
∵AB=BF,AO=EO,
∴∠BFA=∠BAF,∠OEF=∠OAF,
∴∠BAF+∠OAF=∠BFA+∠OEF=90°,
即∠BAO=90°,
∵A为⊙O上的一点,
∴AB是⊙O切线;
(2)设FO=x,则CO=FC﹣FO=4﹣x,
∴EO=CO=4﹣x,
在Rt△EFO中,EO2+FO2=EF2,
∴(4﹣x)2+x2=()2,
解得:x1=1,x2=3(不合题意,舍去),
∴AO=CO=4﹣1=3,
设AB=y,则BO=BF+FO=y+1,
在Rt△ABO中,AO2+AB2=BO2,
∴32+y2=(y+1)2,
解得:y=4,
∴AB=4.
21世纪教育网(www.21cnjy.com)
同课章节目录
