2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练(一)(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练(一)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 507.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 16:50:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练(一)
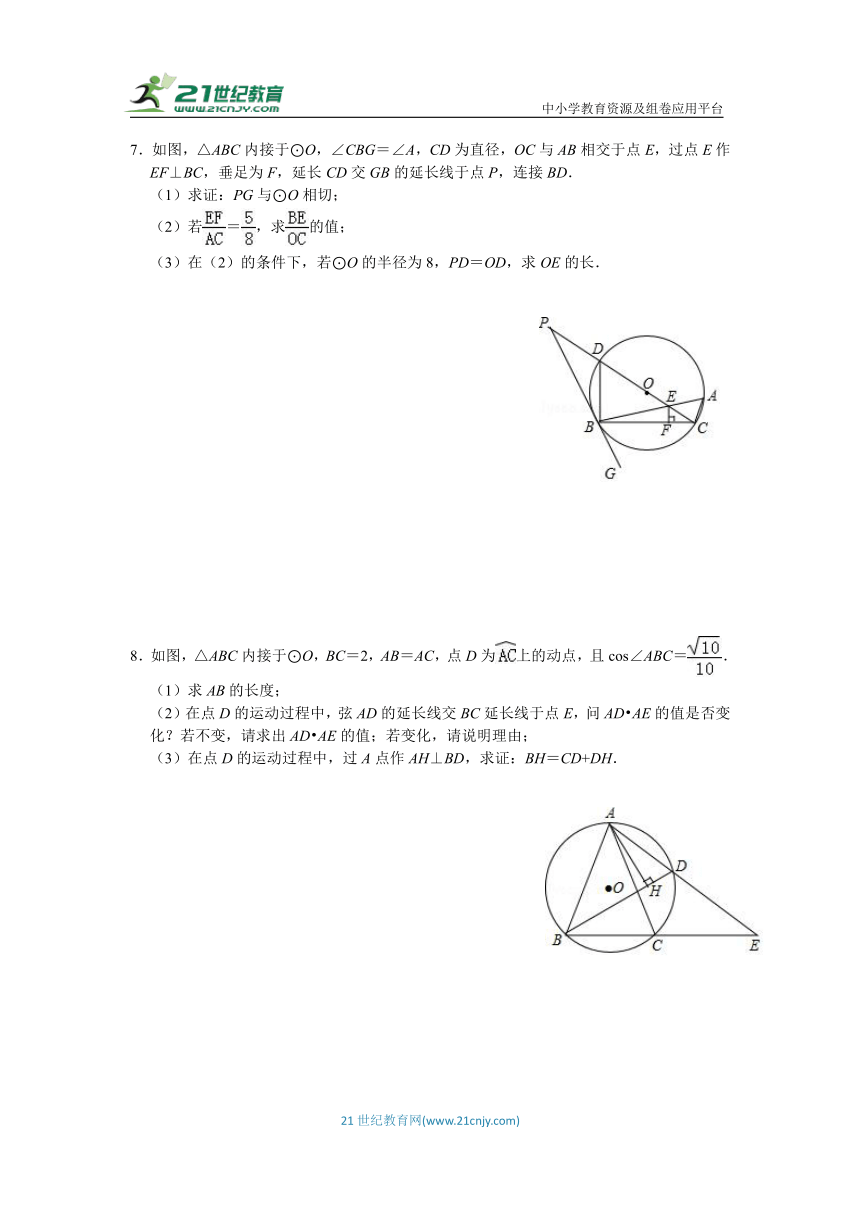
1.如图,AB为⊙O的直径,C,G是⊙O上两点,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F,且BC平分∠ABD.
(1)求证:CD是⊙O的切线;
(2)若=,求∠E的度数;
(3)连结AD,在(2)的条件下,若CD=2,求AD的长.
2.如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,
AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
3.如图,在Rt△ABC中,∠C=90°,点D在线段AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,∠B=∠BAE=30°.
(1)求证:BC是⊙O的切线;
(2)若AC=3,求⊙O的半径r;
(3)在(1)的条件下,判断以A、O、E、F为顶点的四边形为哪种特殊四边形,并说明理由.
4.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG HB的值.
5.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:△DAC∽△DBA;
(2)过点C作⊙O的切线CE交AD于点E,求证:CE=AD;
(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.
6.如图1,已知⊙O是△ADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
(1)求证:AC=BC;
(2)如图2,在图1的基础上做⊙O的直径CF交AB于点E,连接AF,过点A做⊙O的切线AH,若AH∥BC,求∠ACF的度数;
(3)在(2)的条件下,若△ABD的面积为,△ABD与△ABC的面积比为2:9,求CD的长.
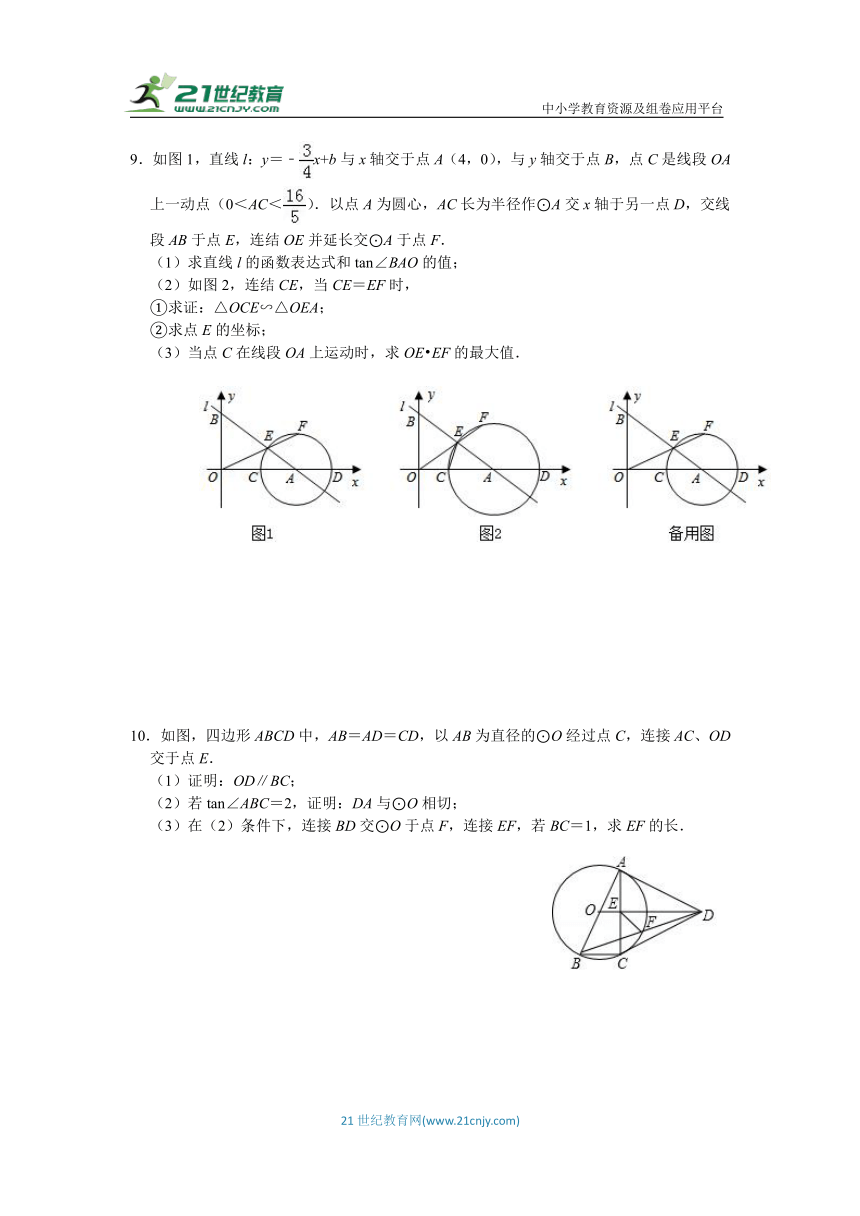
7.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若=,求的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
8.如图,△ABC内接于⊙O,BC=2,AB=AC,点D为上的动点,且cos∠ABC=.
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问AD AE的值是否变化?若不变,请求出AD AE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
9.如图1,直线l:y=﹣x+b与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC<).以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.
(1)求直线l的函数表达式和tan∠BAO的值;
(2)如图2,连结CE,当CE=EF时,
①求证:△OCE∽△OEA;
②求点E的坐标;
(3)当点C在线段OA上运动时,求OE EF的最大值.
10.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.
11.如图,△ABC是⊙O的内接三角形,点D在上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=AB AC;
(3)已知⊙O的半径为3.
①若=,求BC的长;
②当为何值时,AB AC的值最大?
12.如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.
(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长.
②若△BED为等腰三角形,求所有满足条件的BD的长.
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出的值.
13.如图,C、D是以AB为直径的⊙O上的点,=,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CE DE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
14.如图,在以线段AB为直径的⊙O上取一点C,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
15.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
参考答案
1.【解答】证明:(1)连接OC,
∵OC=OB,BC平分∠ABD,
∴∠OCB=∠OBC,∠OBC=∠DBC,
∴∠DBC=∠OCB,
∴OC∥BD,
∴∠BDC=∠ECO,
∵CD⊥BD,
∴∠BDC=90°,
∴∠ECO=90°,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)由(1)知,
OC∥BD,
∴∠OCF=∠DBF,∠COF=∠BDF,
∴△OCF∽△DBD,
∴,
∵=,
∴,
∵OC∥BD,
∴△EOC∽△EDB,
∴,
∴,
设OE=2a,EB=3a,
∴OB=a,
∴OC=a,
∵∠OCE=90°,OC=OE,
∴∠E=30°;
(3)∵∠E=30°,∠BDE=90°,BC平分∠DBE,
∴∠EBD=60°,∠OBC=∠DBC=30°,
∵CD=2,
∴BC=4,BD=6,
∵,
∴OC=4,
作DM⊥AB于点M,
∴∠DBM=90°,
∵BD=6,∠DBM=60°,
∴BM=3,DM=3,
∵OC=4,
∴AB=8,
∴AM=5,
∵∠DMA=90°,DM=3,
∴AD==.
2.【解答】解:(1)证明:连接HB,
∵点H是△ABC的内心,
∴∠DAC=∠DAB,∠ABH=∠CBH,
∵∠DBC=∠DAC,
∴∠DHB=∠DAB+∠ABH=∠DAC+∠CBH,
∵∠DBH=∠DBC+∠CBH,
∴∠DHB=∠DBH,
∴DH=DB;
(2)①连接OD,
∵∠DOB=2∠DAB=∠BAC
∴OD∥AC,
∵AC⊥BC,BC∥EF,
∴AC⊥EF,
∴OD⊥EF,
∵点D在⊙O上,
∴EF是⊙O的切线;
②过点D作DG⊥AB于G,
∵∠EAD=∠DAB,
∴DE=DG,
∵DC=DB,∠CED=∠DGB=90°,
∴△CDE≌△BDG,
∴GB=CE=1,
在Rt△ADB中,DG⊥AB,
∴∠DAB=∠BDG,
∵∠DBG=∠ABD,
∴△DBG∽△ABD,
∴,
∴DB2=AB BG=5×1=5,
∴DB=,DG=2,
∴ED=2,
∵H是内心,
∴AE=AG=4,
∵DO∥AE,
∴△OFD∽△AFE,
∴,
∴,
∴DF=.
3.【解答】解:(1)如图1,
连接OE,∴OA=OE,
∴∠BAE=∠OEA,
∵∠BAE=30°,
∴∠OEA=30°,
∴∠AOE=∠BAE+∠OEA=60°,
在△BOE中,∠B=30°,
∴∠OEB=180°﹣∠B﹣∠BOE=90°,
∴OE⊥BC,
∵点E在⊙O上,
∴BC是⊙O的切线;
(2)如图2,∵∠B=∠BAE=30°,
∴∠AEC=∠B+∠BAE=60°,
在Rt△ACE中,AC=3,sin∠AEC=,
∴AE===2,
连接DE,∵AD是⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,∠BAE=30°,cos∠DAE=,
∴AD===4,
∴⊙O的半径r=AD=2;
(3)以A、O、E、F为顶点的四边形是菱形,理由:如图3,
在Rt△ABC中,∠B=30°,
∴∠BAC=60°,
连接OF,∴OA=OF,
∴△AOF是等边三角形,
∴OA=AF,∠AOF=60°,
连接EF,OE,
∴OE=OF,
∵∠OEB=90°,∠B=30°,
∴∠AOE=90°+30°=120°,
∴∠EOF=∠AOE﹣∠AOF=60°,
∵OE=OF,
∴△OEF是等边三角形,
∴OE=EF,
∵OA=OE,
∴OA=AF=EF=OE,
∴四边形OAFE是菱形.
4.【解答】【解答】解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,∠EBF=90°,
∴∠C=∠DBC,EF为直径,
∴点O在EF上,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF,
∵BC=BF,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴EF==,
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=(EF)2 π=π=π;
(3)∵BH平分∠CBF,
∴=,
∴EH=FH,
∴△EHF是等腰直角三角形,
∴HF=EF=,
∵∠EFH=∠HBF=45°,∠BHF=∠BHF,
∴△BHF∽△FHG,
∴,
∴HG HB=HF2=2+.
5.【解答】解:(1)∵AB是⊙O直径,
∴∠ACD=∠ACB=90°,
∵AD是⊙O的切线,
∴∠BAD=90°,
∴∠ACD=∠DAB=90°,
∵∠D=∠D,
∴△DAC∽△DBA;
(2)∵EA,EC是⊙O的切线,
∴AE=CE(切线长定理),
∴∠DAC=∠ECA,
∵∠ACD=90°,
∴∠ACE+∠DCE=90°,∠DAC+∠D=90°,
∴∠D=∠DCE,
∴DE=CE,
∴AD=AE+DE=CE+CE=2CE,
∴CE=AD;
(3)如图,在Rt△ABD中,AD=6,AB=3,
∴tan∠ABD==2,
过点G作GH⊥BD于H,
∴tan∠ABD==2,
∴GH=2BH,
∵点F是直径AB下方半圆的中点,
∴∠BCF=45°,
∴∠CGH=∠CHG﹣∠BCF=45°,
∴CH=GH=2BH,
∴BC=BH+CH=3BH,
在Rt△ABC中,tan∠ABC==2,
∴AC=2BC,
根据勾股定理得,AC2+BC2=AB2,
∴4BC2+BC2=9,
∴BC=,
∴3BH=,
∴BH=,
∴GH=2BH=,
在Rt△CHG中,∠BCF=45°,
∴CG=GH=.
6.【解答】解:(1)∵DC平分∠ADB,
∴∠ADC=∠BDC,
∴,
∴AC=BC
(2)连接AO并延长交BC于I交⊙O于J,
∵AH是⊙O的切线且AH∥BC,
∴AI⊥BC,
由垂径定理得,BI=IC,
∵AC=BC,
∴IC=AC,
在Rt△AIC中,IC=AC,
∴∠IAC=30°
∴∠ABC=60°=∠F=∠ACB,
∵FC是直径,
∴∠FAC=90°,
∴∠ACF=180°﹣90°﹣60°=30°;
(3)过点D作DG⊥AB,连接AO
由(1)(2)知,△ABC为等边三角形,
∵∠ACF=30°,
∴AB⊥CF,
∴AE=BE,
∴,
∴AB=,
∴,
在Rt△AEC中,CE=AE=9,
在Rt△AEO中,设EO=x,则AO=2x,
∴AO2=AE2+OE2,
∴,
∴x=6,
∴⊙O的半径为6,
∴CF=12,
∵,
∴DG=2,
过点D作DP⊥CF,连接OD,
∵AB⊥CF,DG⊥AB,
∴CF∥DG,
∴四边形PDGE为矩形,
∴PE=DG=2,
∴CP=PE+CE=2+9=11
在Rt△OPD中,OP=5,OD=6,
∴DP==,
∴在Rt△CPD中,根据勾股定理得,CD==2.
7.【解答】解:(1)如图,连接OB,则OB=OD,
∴∠BDC=∠DBO,
∵∠BAC=∠BDC、∠BDC=∠GBC,
∴∠GBC=∠BDC,
∵CD是⊙O的直径,
∴∠DBO+∠OBC=90°,
∴∠GBC+∠OBC=90°,
∴∠GBO=90°,
∴PG与⊙O相切;
(2)过点O作OM⊥AC于点M,连接OA,
则∠AOM=∠COM=∠AOC,
∵=,
∴∠ABC=∠AOC,
又∵∠EFB=∠OMA=90°,
∴△BEF∽△OAM,
∴=,
∵AM=AC,OA=OC,
∴=,
又∵=,
∴=2×=2×=;
(3)∵PD=OD,∠PBO=90°,
∴BD=OD=8,
在Rt△DBC中,BC==8,
又∵OD=OB,
∴△DOB是等边三角形,
∴∠DOB=60°,
∵∠DOB=∠OBC+∠OCB,OB=OC,
∴∠OCB=30°,
∴=,=,
∴可设EF=x,则EC=2x、FC=x,
∴BF=8﹣x,
在Rt△BEF中,BE2=EF2+BF2,
∴100=x2+(8﹣x)2,
解得:x=6±,
∵6+>8,舍去,
∴x=6﹣,
∴EC=12﹣2,
∴OE=8﹣(12﹣2)=2﹣4.
8.【解答】解:(1)作AM⊥BC,
∵AB=AC,AM⊥BC,BC=2BM,
∴CM=BC=1,
∵cosB==,
在Rt△AMB中,BM=1,
∴AB==;
(2)连接DC,
∵AB=AC,
∴∠ACB=∠ABC,
∵四边形ABCD内接于圆O,
∴∠ADC+∠ABC=180°,
∵∠ACE+∠ACB=180°,
∴∠ADC=∠ACE,
∵∠CAE公共角,
∴△EAC∽△CAD,
∴=,
∴AD AE=AC2=10;
(3)在BD上取一点N,使得BN=CD,
在△ABN和△ACD中
,
∴△ABN≌△ACD(SAS),
∴AN=AD,
∵AN=AD,AH⊥BD,
∴NH=HD,
∵BN=CD,NH=HD,
∴BN+NH=CD+HD=BH.
9.【解答】解:∵直线l:y=﹣x+b与x轴交于点A(4,0),
∴﹣×4+b=0,
∴b=3,
∴直线l的函数表达式y=﹣x+3,
∴B(0,3),
∴OA=4,OB=3,
在Rt△AOB中,tan∠BAO==;
(2)①如图2,连接DF,∵CE=EF,
∴∠CDE=∠FDE,
∴∠CDF=2∠CDE,
∵∠OAE=2∠CDE,
∴∠OAE=∠ODF,
∵四边形CEFD是⊙O的圆内接四边形,
∴∠OEC=∠ODF,
∴∠OEC=∠OAE,
∵∠COE=∠EOA,
∴△COE∽△EOA,
②过点E⊥OA于M,
由①知,tan∠OAB=,
设EM=3m,则AM=4m,
∴OM=4﹣4m,AE=5m,
∴E(4﹣4m,3m),AC=5m,∴
OC=4﹣5m,
由①知,△COE∽△EOA,
∴,
∴OE2=OA OC=4(4﹣5m)=16﹣20m,
∵E(4﹣4m,3m),
∴(4﹣4m)2+9m2=25m2﹣32m+16,
∴25m2﹣32m+16=16﹣20m,
∴m=0(舍)或m=,
∴4﹣4m=,3m=,
∴E(,),
(3)如图,设⊙O的半径为r,过点O作OG⊥AB于G,
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=5,
∴AB×OG=OA×OB,
∴OG=,
∴AG==×=,
∴EG=AG﹣AE=﹣r,
连接FH,
∵EH是⊙O直径,
∴EH=2r,∠EFH=90°=∠EGO,
∵∠OEG=∠HEF,
∴△OEG∽△HEF,
∴,
∴OE EF=HE EG=2r(﹣r)=﹣2(r﹣)2+,
∴r=时,OE EF最大值为.
10.【解答】解:(1)连接OC,
在△OAD和△OCD中,
∵,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=90°,即BC⊥AC,
∴OD∥BC;
(2)∵tan∠ABC==2,
∴设BC=a、则AC=2a,
∴AD=AB==,
∵OE∥BC,且AO=BO,
∴OE=BC=a,AE=CE=AC=a,
在△AED中,DE==2a,
在△AOD中,AO2+AD2=()2+(a)2=a2,OD2=(OE+DE)2=(a+2a)2=a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
则DA与⊙O相切;
(3)连接AF,
∵AB是⊙O的直径,
∴∠AFD=∠BAD=90°,
∵∠ADF=∠BDA,
∴△AFD∽△BAD,
∴=,即DF BD=AD2①,
又∵∠AED=∠OAD=90°,∠ADE=∠ODA,
∴△AED∽△OAD,
∴=,即OD DE=AD2②,
由①②可得DF BD=OD DE,即=,
又∵∠EDF=∠BDO,
∴△EDF∽△BDO,
∵BC=1,
∴AB=AD=、OD=、ED=2、BD=、OB=,
∴=,即=,
解得:EF=.
11.【解答】解:(1)∵四边形EBDC为菱形,
∴∠D=∠BEC,
∵四边形ABDC是圆的内接四边形,
∴∠A+∠D=180°,
又∠BEC+∠AEC=180°,
∴∠A=∠AEC,
∴AC=AE;
(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,
由(1)知AC=CE=CD,
∴CF=CG=AC,
∵四边形AEFG是⊙C的内接四边形,
∴∠G+∠AEF=180°,
又∵∠AEF+∠BEF=180°,
∴∠G=∠BEF,
∵∠EBF=∠GBA,
∴△BEF∽△BGA,
∴=,即BF BG=BE AB,
∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,
∴(BC﹣AC)(BC+AC)=AB AC,即BC2﹣AC2=AB AC;
(3)设AB=5k、AC=3k,
∵BC2﹣AC2=AB AC,
∴BC=2k,
连接ED交BC于点M,
∵四边形BDCE是菱形,
∴DE垂直平分BC,
则点E、O、M、D共线,
在Rt△DMC中,DC=AC=3k,MC=BC=k,
∴DM==k,
∴OM=OD﹣DM=3﹣k,
在Rt△COM中,由OM2+MC2=OC2得(3﹣k)2+(k)2=32,
解得:k=或k=0(舍),
∴BC=2k=4;
②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,
∴BC2=(2MC)2=36﹣4d2,
AC2=DC2=DM2+CM2=(3﹣d)2+9﹣d2,
由(2)得AB AC=BC2﹣AC2
=﹣4d2+6d+18
=﹣4(d﹣)2+,
∴当d=,即OM=时,AB AC最大,最大值为,
∴DC2=,
∴AC=DC=,
∴AB=,此时=.
12.【解答】解:(1)∵PB⊥AM、PC⊥AN,
∴∠ABP=∠ACP=90°,
∴∠BAC+∠BPC=180°,
又∠BPD+∠BPC=180°,
∴∠BPD=∠BAC;
(2)①如图1,
∵∠APB=∠BDE=45°,∠ABP=90°,
∴BP=AB=2,
∵∠BPD=∠BAC,
∴tan∠BPD=tan∠BAC,
∴=2,
∴BP=PD,
∴PD=2;
②当BD=BE时,∠BED=∠BDE,
∴∠BPD=∠BPE=∠BAC,
∴tan∠BPE=2,
∵AB=2,
∴BP=,
∴BD=2;
当BE=DE时,∠EBD=∠EDB,
∵∠APB=∠BDE、∠DBE=∠APC,
∴∠APB=∠APC,
∴AC=AB=2,
过点B作BG⊥AC于点G,得四边形BGCD是矩形,
∵AB=2、tan∠BAC=2,
∴AG=2,
∴BD=CG=2﹣2;
当BD=DE时,∠DEB=∠DBE=∠APC,
∵∠DEB=∠DPB=∠BAC,
∴∠APC=∠BAC,
设PD=x,则BD=2x,
∴=2,
∴,
∴x=,
∴BD=2x=3,
综上所述,当BD=2、3或2﹣2时,△BDE为等腰三角形;
(3)如图3,过点O作OH⊥DC于点H,
∵tan∠BPD=tan∠MAN=1,
∴BD=PD,
设BD=PD=2a、PC=2b,
则OH=a、CH=a+2b、AC=4a+2b,
∵OC∥BE且∠BEP=90°,
∴∠PFC=90°,
∴∠PAC+∠APC=∠OCH+∠APC=90°,
∴∠OCH=∠PAC,
∴△ACP∽△CHO,
∴=,即OH AC=CH PC,
∴a(4a+2b)=2b(a+2b),
∴a=b,
即CP=2a、CH=3a,
则OC=a,
∵△CPF∽△COH,
∴=,即=,
则CF=a,OF=OC﹣CF=a,
∵BE∥OC且BO=PO,
∴OF为△PBE的中位线,
∴EF=PF,
∴==.
13.【解答】解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,即∠BAD+∠ABD=90°,
∵PB是⊙O的切线,
∴∠ABP=90°,即∠PBD+∠ABD=90°,
∴∠BAD=∠PBD;
(2)∵∠A=∠C、∠AED=∠CEB,
∴△ADE∽△CBE,
∴=,即DE CE=AE BE,
如图,连接OC,
设圆的半径为r,则OA=OB=OC=r,
则DE CE=AE BE=(OA﹣OE)(OB+OE)=r2﹣OE2,
∵=,
∴∠AOC=∠BOC=90°,
∴CE2=OE2+OC2=OE2+r2,BC2=BO2+CO2=2r2,
则BC2﹣CE2=2r2﹣(OE2+r2)=r2﹣OE2,
∴BC2﹣CE2=DE CE;
(3)∵OA=4,
∴OB=OC=OA=4,
∴BC==4,
又∵E是半径OA的中点,
∴AE=OE=2,
则CE===2,
∵BC2﹣CE2=DE CE,
∴(4)2﹣(2)2=DE 2,
解得:DE=.
14.【解答】解:(1)∵AB为⊙O的直径,
∴∠C=90°,
∵将△ABC沿AB翻折后得到△ABD,
∴△ABC≌△ABD,
∴∠ADB=∠C=90°,
连接OD,
则OD=AO=BO,
∴点D在以AB为直径的⊙O上;
(2)∵△ABC≌△ABD,
∴AC=AD,
∵AB2=AC AE,
∴AB2=AD AE,即=,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴∠ABE=∠ADB=90°,
∵AB为⊙O的直径,
∴BE是⊙O的切线;
(3)∵AD=AC=4、BD=BC=2,∠ADB=90°,
∴AB===2,
∵=,
∴=,
解得:DE=1,
∴BE==,
∵四边形ACBD内接于⊙O,
∴∠FBD=∠FAC,即∠FBE+∠DBE=∠BAE+∠BAC,
又∵∠DBE+∠ABD=∠BAE+∠ABD=90°,
∴∠DBE=∠BAE,
∴∠FBE=∠BAC,
又∠BAC=∠BAD,
∴∠FBE=∠BAD,
∴△FBE∽△FAB,
∴=,即==,
∴FB=2FE,
在Rt△ACF中,∵AF2=AC2+CF2,
∴(5+EF)2=42+(2+2EF)2,
整理,得:3EF2﹣2EF﹣5=0,
解得:EF=﹣1(舍)或EF=,
∴EF=.
15.【解答】解:(1)直线l与⊙O相切.
理由:如图1所示:连接OE.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴.
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切.
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴,即,解得;AE=.
∴AF=AE﹣EF=﹣7=.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练(一)
1.如图,AB为⊙O的直径,C,G是⊙O上两点,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F,且BC平分∠ABD.
(1)求证:CD是⊙O的切线;
(2)若=,求∠E的度数;
(3)连结AD,在(2)的条件下,若CD=2,求AD的长.
2.如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,
AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
3.如图,在Rt△ABC中,∠C=90°,点D在线段AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,∠B=∠BAE=30°.
(1)求证:BC是⊙O的切线;
(2)若AC=3,求⊙O的半径r;
(3)在(1)的条件下,判断以A、O、E、F为顶点的四边形为哪种特殊四边形,并说明理由.
4.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG HB的值.
5.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:△DAC∽△DBA;
(2)过点C作⊙O的切线CE交AD于点E,求证:CE=AD;
(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.
6.如图1,已知⊙O是△ADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
(1)求证:AC=BC;
(2)如图2,在图1的基础上做⊙O的直径CF交AB于点E,连接AF,过点A做⊙O的切线AH,若AH∥BC,求∠ACF的度数;
(3)在(2)的条件下,若△ABD的面积为,△ABD与△ABC的面积比为2:9,求CD的长.
7.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若=,求的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
8.如图,△ABC内接于⊙O,BC=2,AB=AC,点D为上的动点,且cos∠ABC=.
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问AD AE的值是否变化?若不变,请求出AD AE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
9.如图1,直线l:y=﹣x+b与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC<).以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.
(1)求直线l的函数表达式和tan∠BAO的值;
(2)如图2,连结CE,当CE=EF时,
①求证:△OCE∽△OEA;
②求点E的坐标;
(3)当点C在线段OA上运动时,求OE EF的最大值.
10.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.
11.如图,△ABC是⊙O的内接三角形,点D在上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=AB AC;
(3)已知⊙O的半径为3.
①若=,求BC的长;
②当为何值时,AB AC的值最大?
12.如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.
(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长.
②若△BED为等腰三角形,求所有满足条件的BD的长.
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出的值.
13.如图,C、D是以AB为直径的⊙O上的点,=,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CE DE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
14.如图,在以线段AB为直径的⊙O上取一点C,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
15.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
参考答案
1.【解答】证明:(1)连接OC,
∵OC=OB,BC平分∠ABD,
∴∠OCB=∠OBC,∠OBC=∠DBC,
∴∠DBC=∠OCB,
∴OC∥BD,
∴∠BDC=∠ECO,
∵CD⊥BD,
∴∠BDC=90°,
∴∠ECO=90°,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)由(1)知,
OC∥BD,
∴∠OCF=∠DBF,∠COF=∠BDF,
∴△OCF∽△DBD,
∴,
∵=,
∴,
∵OC∥BD,
∴△EOC∽△EDB,
∴,
∴,
设OE=2a,EB=3a,
∴OB=a,
∴OC=a,
∵∠OCE=90°,OC=OE,
∴∠E=30°;
(3)∵∠E=30°,∠BDE=90°,BC平分∠DBE,
∴∠EBD=60°,∠OBC=∠DBC=30°,
∵CD=2,
∴BC=4,BD=6,
∵,
∴OC=4,
作DM⊥AB于点M,
∴∠DBM=90°,
∵BD=6,∠DBM=60°,
∴BM=3,DM=3,
∵OC=4,
∴AB=8,
∴AM=5,
∵∠DMA=90°,DM=3,
∴AD==.
2.【解答】解:(1)证明:连接HB,
∵点H是△ABC的内心,
∴∠DAC=∠DAB,∠ABH=∠CBH,
∵∠DBC=∠DAC,
∴∠DHB=∠DAB+∠ABH=∠DAC+∠CBH,
∵∠DBH=∠DBC+∠CBH,
∴∠DHB=∠DBH,
∴DH=DB;
(2)①连接OD,
∵∠DOB=2∠DAB=∠BAC
∴OD∥AC,
∵AC⊥BC,BC∥EF,
∴AC⊥EF,
∴OD⊥EF,
∵点D在⊙O上,
∴EF是⊙O的切线;
②过点D作DG⊥AB于G,
∵∠EAD=∠DAB,
∴DE=DG,
∵DC=DB,∠CED=∠DGB=90°,
∴△CDE≌△BDG,
∴GB=CE=1,
在Rt△ADB中,DG⊥AB,
∴∠DAB=∠BDG,
∵∠DBG=∠ABD,
∴△DBG∽△ABD,
∴,
∴DB2=AB BG=5×1=5,
∴DB=,DG=2,
∴ED=2,
∵H是内心,
∴AE=AG=4,
∵DO∥AE,
∴△OFD∽△AFE,
∴,
∴,
∴DF=.
3.【解答】解:(1)如图1,
连接OE,∴OA=OE,
∴∠BAE=∠OEA,
∵∠BAE=30°,
∴∠OEA=30°,
∴∠AOE=∠BAE+∠OEA=60°,
在△BOE中,∠B=30°,
∴∠OEB=180°﹣∠B﹣∠BOE=90°,
∴OE⊥BC,
∵点E在⊙O上,
∴BC是⊙O的切线;
(2)如图2,∵∠B=∠BAE=30°,
∴∠AEC=∠B+∠BAE=60°,
在Rt△ACE中,AC=3,sin∠AEC=,
∴AE===2,
连接DE,∵AD是⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,∠BAE=30°,cos∠DAE=,
∴AD===4,
∴⊙O的半径r=AD=2;
(3)以A、O、E、F为顶点的四边形是菱形,理由:如图3,
在Rt△ABC中,∠B=30°,
∴∠BAC=60°,
连接OF,∴OA=OF,
∴△AOF是等边三角形,
∴OA=AF,∠AOF=60°,
连接EF,OE,
∴OE=OF,
∵∠OEB=90°,∠B=30°,
∴∠AOE=90°+30°=120°,
∴∠EOF=∠AOE﹣∠AOF=60°,
∵OE=OF,
∴△OEF是等边三角形,
∴OE=EF,
∵OA=OE,
∴OA=AF=EF=OE,
∴四边形OAFE是菱形.
4.【解答】【解答】解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,∠EBF=90°,
∴∠C=∠DBC,EF为直径,
∴点O在EF上,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF,
∵BC=BF,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴EF==,
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=(EF)2 π=π=π;
(3)∵BH平分∠CBF,
∴=,
∴EH=FH,
∴△EHF是等腰直角三角形,
∴HF=EF=,
∵∠EFH=∠HBF=45°,∠BHF=∠BHF,
∴△BHF∽△FHG,
∴,
∴HG HB=HF2=2+.
5.【解答】解:(1)∵AB是⊙O直径,
∴∠ACD=∠ACB=90°,
∵AD是⊙O的切线,
∴∠BAD=90°,
∴∠ACD=∠DAB=90°,
∵∠D=∠D,
∴△DAC∽△DBA;
(2)∵EA,EC是⊙O的切线,
∴AE=CE(切线长定理),
∴∠DAC=∠ECA,
∵∠ACD=90°,
∴∠ACE+∠DCE=90°,∠DAC+∠D=90°,
∴∠D=∠DCE,
∴DE=CE,
∴AD=AE+DE=CE+CE=2CE,
∴CE=AD;
(3)如图,在Rt△ABD中,AD=6,AB=3,
∴tan∠ABD==2,
过点G作GH⊥BD于H,
∴tan∠ABD==2,
∴GH=2BH,
∵点F是直径AB下方半圆的中点,
∴∠BCF=45°,
∴∠CGH=∠CHG﹣∠BCF=45°,
∴CH=GH=2BH,
∴BC=BH+CH=3BH,
在Rt△ABC中,tan∠ABC==2,
∴AC=2BC,
根据勾股定理得,AC2+BC2=AB2,
∴4BC2+BC2=9,
∴BC=,
∴3BH=,
∴BH=,
∴GH=2BH=,
在Rt△CHG中,∠BCF=45°,
∴CG=GH=.
6.【解答】解:(1)∵DC平分∠ADB,
∴∠ADC=∠BDC,
∴,
∴AC=BC
(2)连接AO并延长交BC于I交⊙O于J,
∵AH是⊙O的切线且AH∥BC,
∴AI⊥BC,
由垂径定理得,BI=IC,
∵AC=BC,
∴IC=AC,
在Rt△AIC中,IC=AC,
∴∠IAC=30°
∴∠ABC=60°=∠F=∠ACB,
∵FC是直径,
∴∠FAC=90°,
∴∠ACF=180°﹣90°﹣60°=30°;
(3)过点D作DG⊥AB,连接AO
由(1)(2)知,△ABC为等边三角形,
∵∠ACF=30°,
∴AB⊥CF,
∴AE=BE,
∴,
∴AB=,
∴,
在Rt△AEC中,CE=AE=9,
在Rt△AEO中,设EO=x,则AO=2x,
∴AO2=AE2+OE2,
∴,
∴x=6,
∴⊙O的半径为6,
∴CF=12,
∵,
∴DG=2,
过点D作DP⊥CF,连接OD,
∵AB⊥CF,DG⊥AB,
∴CF∥DG,
∴四边形PDGE为矩形,
∴PE=DG=2,
∴CP=PE+CE=2+9=11
在Rt△OPD中,OP=5,OD=6,
∴DP==,
∴在Rt△CPD中,根据勾股定理得,CD==2.
7.【解答】解:(1)如图,连接OB,则OB=OD,
∴∠BDC=∠DBO,
∵∠BAC=∠BDC、∠BDC=∠GBC,
∴∠GBC=∠BDC,
∵CD是⊙O的直径,
∴∠DBO+∠OBC=90°,
∴∠GBC+∠OBC=90°,
∴∠GBO=90°,
∴PG与⊙O相切;
(2)过点O作OM⊥AC于点M,连接OA,
则∠AOM=∠COM=∠AOC,
∵=,
∴∠ABC=∠AOC,
又∵∠EFB=∠OMA=90°,
∴△BEF∽△OAM,
∴=,
∵AM=AC,OA=OC,
∴=,
又∵=,
∴=2×=2×=;
(3)∵PD=OD,∠PBO=90°,
∴BD=OD=8,
在Rt△DBC中,BC==8,
又∵OD=OB,
∴△DOB是等边三角形,
∴∠DOB=60°,
∵∠DOB=∠OBC+∠OCB,OB=OC,
∴∠OCB=30°,
∴=,=,
∴可设EF=x,则EC=2x、FC=x,
∴BF=8﹣x,
在Rt△BEF中,BE2=EF2+BF2,
∴100=x2+(8﹣x)2,
解得:x=6±,
∵6+>8,舍去,
∴x=6﹣,
∴EC=12﹣2,
∴OE=8﹣(12﹣2)=2﹣4.
8.【解答】解:(1)作AM⊥BC,
∵AB=AC,AM⊥BC,BC=2BM,
∴CM=BC=1,
∵cosB==,
在Rt△AMB中,BM=1,
∴AB==;
(2)连接DC,
∵AB=AC,
∴∠ACB=∠ABC,
∵四边形ABCD内接于圆O,
∴∠ADC+∠ABC=180°,
∵∠ACE+∠ACB=180°,
∴∠ADC=∠ACE,
∵∠CAE公共角,
∴△EAC∽△CAD,
∴=,
∴AD AE=AC2=10;
(3)在BD上取一点N,使得BN=CD,
在△ABN和△ACD中
,
∴△ABN≌△ACD(SAS),
∴AN=AD,
∵AN=AD,AH⊥BD,
∴NH=HD,
∵BN=CD,NH=HD,
∴BN+NH=CD+HD=BH.
9.【解答】解:∵直线l:y=﹣x+b与x轴交于点A(4,0),
∴﹣×4+b=0,
∴b=3,
∴直线l的函数表达式y=﹣x+3,
∴B(0,3),
∴OA=4,OB=3,
在Rt△AOB中,tan∠BAO==;
(2)①如图2,连接DF,∵CE=EF,
∴∠CDE=∠FDE,
∴∠CDF=2∠CDE,
∵∠OAE=2∠CDE,
∴∠OAE=∠ODF,
∵四边形CEFD是⊙O的圆内接四边形,
∴∠OEC=∠ODF,
∴∠OEC=∠OAE,
∵∠COE=∠EOA,
∴△COE∽△EOA,
②过点E⊥OA于M,
由①知,tan∠OAB=,
设EM=3m,则AM=4m,
∴OM=4﹣4m,AE=5m,
∴E(4﹣4m,3m),AC=5m,∴
OC=4﹣5m,
由①知,△COE∽△EOA,
∴,
∴OE2=OA OC=4(4﹣5m)=16﹣20m,
∵E(4﹣4m,3m),
∴(4﹣4m)2+9m2=25m2﹣32m+16,
∴25m2﹣32m+16=16﹣20m,
∴m=0(舍)或m=,
∴4﹣4m=,3m=,
∴E(,),
(3)如图,设⊙O的半径为r,过点O作OG⊥AB于G,
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=5,
∴AB×OG=OA×OB,
∴OG=,
∴AG==×=,
∴EG=AG﹣AE=﹣r,
连接FH,
∵EH是⊙O直径,
∴EH=2r,∠EFH=90°=∠EGO,
∵∠OEG=∠HEF,
∴△OEG∽△HEF,
∴,
∴OE EF=HE EG=2r(﹣r)=﹣2(r﹣)2+,
∴r=时,OE EF最大值为.
10.【解答】解:(1)连接OC,
在△OAD和△OCD中,
∵,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=90°,即BC⊥AC,
∴OD∥BC;
(2)∵tan∠ABC==2,
∴设BC=a、则AC=2a,
∴AD=AB==,
∵OE∥BC,且AO=BO,
∴OE=BC=a,AE=CE=AC=a,
在△AED中,DE==2a,
在△AOD中,AO2+AD2=()2+(a)2=a2,OD2=(OE+DE)2=(a+2a)2=a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
则DA与⊙O相切;
(3)连接AF,
∵AB是⊙O的直径,
∴∠AFD=∠BAD=90°,
∵∠ADF=∠BDA,
∴△AFD∽△BAD,
∴=,即DF BD=AD2①,
又∵∠AED=∠OAD=90°,∠ADE=∠ODA,
∴△AED∽△OAD,
∴=,即OD DE=AD2②,
由①②可得DF BD=OD DE,即=,
又∵∠EDF=∠BDO,
∴△EDF∽△BDO,
∵BC=1,
∴AB=AD=、OD=、ED=2、BD=、OB=,
∴=,即=,
解得:EF=.
11.【解答】解:(1)∵四边形EBDC为菱形,
∴∠D=∠BEC,
∵四边形ABDC是圆的内接四边形,
∴∠A+∠D=180°,
又∠BEC+∠AEC=180°,
∴∠A=∠AEC,
∴AC=AE;
(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,
由(1)知AC=CE=CD,
∴CF=CG=AC,
∵四边形AEFG是⊙C的内接四边形,
∴∠G+∠AEF=180°,
又∵∠AEF+∠BEF=180°,
∴∠G=∠BEF,
∵∠EBF=∠GBA,
∴△BEF∽△BGA,
∴=,即BF BG=BE AB,
∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,
∴(BC﹣AC)(BC+AC)=AB AC,即BC2﹣AC2=AB AC;
(3)设AB=5k、AC=3k,
∵BC2﹣AC2=AB AC,
∴BC=2k,
连接ED交BC于点M,
∵四边形BDCE是菱形,
∴DE垂直平分BC,
则点E、O、M、D共线,
在Rt△DMC中,DC=AC=3k,MC=BC=k,
∴DM==k,
∴OM=OD﹣DM=3﹣k,
在Rt△COM中,由OM2+MC2=OC2得(3﹣k)2+(k)2=32,
解得:k=或k=0(舍),
∴BC=2k=4;
②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,
∴BC2=(2MC)2=36﹣4d2,
AC2=DC2=DM2+CM2=(3﹣d)2+9﹣d2,
由(2)得AB AC=BC2﹣AC2
=﹣4d2+6d+18
=﹣4(d﹣)2+,
∴当d=,即OM=时,AB AC最大,最大值为,
∴DC2=,
∴AC=DC=,
∴AB=,此时=.
12.【解答】解:(1)∵PB⊥AM、PC⊥AN,
∴∠ABP=∠ACP=90°,
∴∠BAC+∠BPC=180°,
又∠BPD+∠BPC=180°,
∴∠BPD=∠BAC;
(2)①如图1,
∵∠APB=∠BDE=45°,∠ABP=90°,
∴BP=AB=2,
∵∠BPD=∠BAC,
∴tan∠BPD=tan∠BAC,
∴=2,
∴BP=PD,
∴PD=2;
②当BD=BE时,∠BED=∠BDE,
∴∠BPD=∠BPE=∠BAC,
∴tan∠BPE=2,
∵AB=2,
∴BP=,
∴BD=2;
当BE=DE时,∠EBD=∠EDB,
∵∠APB=∠BDE、∠DBE=∠APC,
∴∠APB=∠APC,
∴AC=AB=2,
过点B作BG⊥AC于点G,得四边形BGCD是矩形,
∵AB=2、tan∠BAC=2,
∴AG=2,
∴BD=CG=2﹣2;
当BD=DE时,∠DEB=∠DBE=∠APC,
∵∠DEB=∠DPB=∠BAC,
∴∠APC=∠BAC,
设PD=x,则BD=2x,
∴=2,
∴,
∴x=,
∴BD=2x=3,
综上所述,当BD=2、3或2﹣2时,△BDE为等腰三角形;
(3)如图3,过点O作OH⊥DC于点H,
∵tan∠BPD=tan∠MAN=1,
∴BD=PD,
设BD=PD=2a、PC=2b,
则OH=a、CH=a+2b、AC=4a+2b,
∵OC∥BE且∠BEP=90°,
∴∠PFC=90°,
∴∠PAC+∠APC=∠OCH+∠APC=90°,
∴∠OCH=∠PAC,
∴△ACP∽△CHO,
∴=,即OH AC=CH PC,
∴a(4a+2b)=2b(a+2b),
∴a=b,
即CP=2a、CH=3a,
则OC=a,
∵△CPF∽△COH,
∴=,即=,
则CF=a,OF=OC﹣CF=a,
∵BE∥OC且BO=PO,
∴OF为△PBE的中位线,
∴EF=PF,
∴==.
13.【解答】解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,即∠BAD+∠ABD=90°,
∵PB是⊙O的切线,
∴∠ABP=90°,即∠PBD+∠ABD=90°,
∴∠BAD=∠PBD;
(2)∵∠A=∠C、∠AED=∠CEB,
∴△ADE∽△CBE,
∴=,即DE CE=AE BE,
如图,连接OC,
设圆的半径为r,则OA=OB=OC=r,
则DE CE=AE BE=(OA﹣OE)(OB+OE)=r2﹣OE2,
∵=,
∴∠AOC=∠BOC=90°,
∴CE2=OE2+OC2=OE2+r2,BC2=BO2+CO2=2r2,
则BC2﹣CE2=2r2﹣(OE2+r2)=r2﹣OE2,
∴BC2﹣CE2=DE CE;
(3)∵OA=4,
∴OB=OC=OA=4,
∴BC==4,
又∵E是半径OA的中点,
∴AE=OE=2,
则CE===2,
∵BC2﹣CE2=DE CE,
∴(4)2﹣(2)2=DE 2,
解得:DE=.
14.【解答】解:(1)∵AB为⊙O的直径,
∴∠C=90°,
∵将△ABC沿AB翻折后得到△ABD,
∴△ABC≌△ABD,
∴∠ADB=∠C=90°,
连接OD,
则OD=AO=BO,
∴点D在以AB为直径的⊙O上;
(2)∵△ABC≌△ABD,
∴AC=AD,
∵AB2=AC AE,
∴AB2=AD AE,即=,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴∠ABE=∠ADB=90°,
∵AB为⊙O的直径,
∴BE是⊙O的切线;
(3)∵AD=AC=4、BD=BC=2,∠ADB=90°,
∴AB===2,
∵=,
∴=,
解得:DE=1,
∴BE==,
∵四边形ACBD内接于⊙O,
∴∠FBD=∠FAC,即∠FBE+∠DBE=∠BAE+∠BAC,
又∵∠DBE+∠ABD=∠BAE+∠ABD=90°,
∴∠DBE=∠BAE,
∴∠FBE=∠BAC,
又∠BAC=∠BAD,
∴∠FBE=∠BAD,
∴△FBE∽△FAB,
∴=,即==,
∴FB=2FE,
在Rt△ACF中,∵AF2=AC2+CF2,
∴(5+EF)2=42+(2+2EF)2,
整理,得:3EF2﹣2EF﹣5=0,
解得:EF=﹣1(舍)或EF=,
∴EF=.
15.【解答】解:(1)直线l与⊙O相切.
理由:如图1所示:连接OE.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴.
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切.
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴,即,解得;AE=.
∴AF=AE﹣EF=﹣7=.
21世纪教育网(www.21cnjy.com)
同课章节目录
