2025年中考数学专项突破练:解一元二次方程组(含解析)
文档属性
| 名称 | 2025年中考数学专项突破练:解一元二次方程组(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 21:52:02 | ||
图片预览



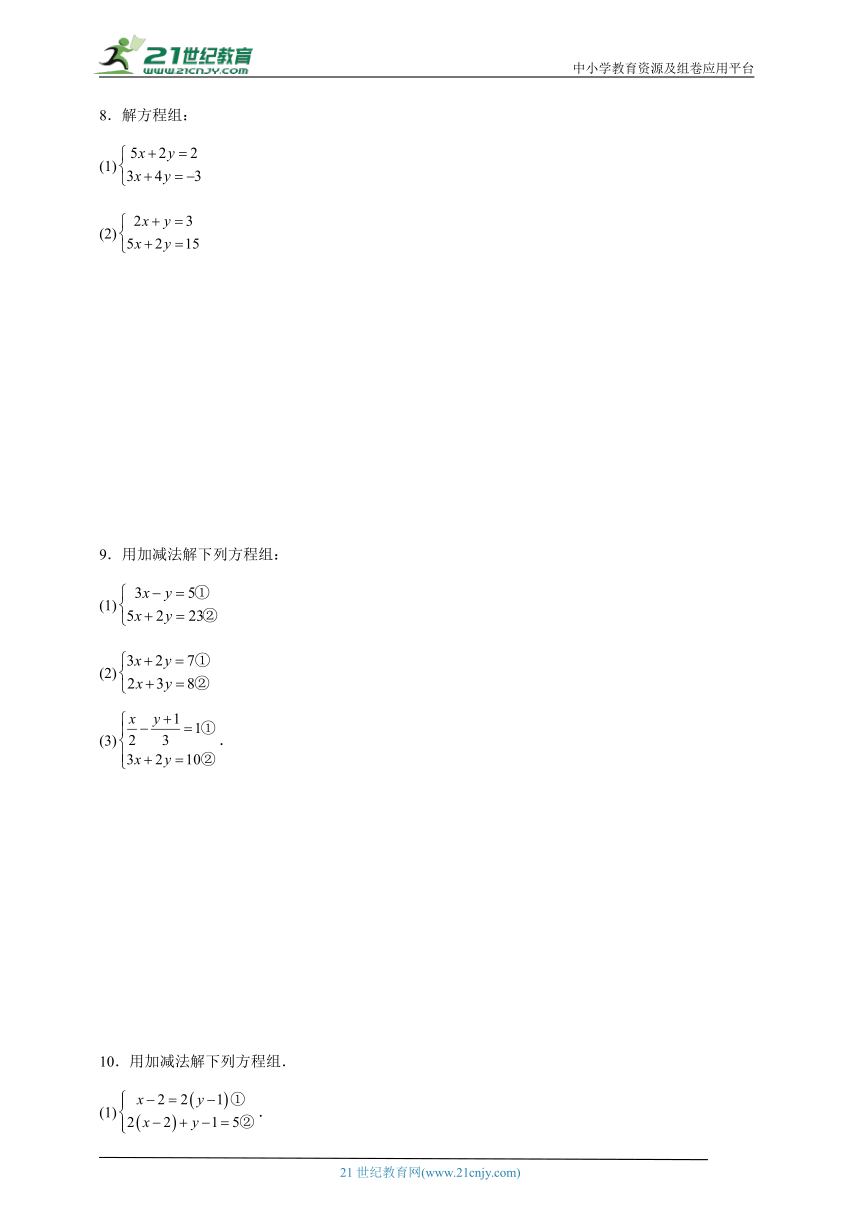

文档简介
中小学教育资源及组卷应用平台
2025年中考数学专项突破练:解一元二次方程组
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.解方程组:
2.解方程组:
(1)
(2)
3.解方程组:
(1)
(2)
4.解方程组:
(1);
(2).
5.解方程组:
(1)
(2)
6.解方程组:
(1) ;
(2).
7.解下列方程组
(1)
(2)
8.解方程组:
(1)
(2)
9.用加减法解下列方程组:
(1)
(2)
(3).
10.用加减法解下列方程组.
(1).
(2).
11.用加减法解下列方程组:
(1);
(2).
12.用加减法解下列方程组:
(1);
(2);
(3);
(4).
13.解下列方程组:
(1)
(2)
14.解下列方程组:
(1);
(2);
(3);
(4).
15.解二元一次方程组
(1)
(2)
16.解下列方程组:
(1)
(2)
17.解方程组:
(1)
(2)
18.解方程组:
(1)
(2)
19.解方程组:
(1)
(2)
20.解下列方程组:
(1);
(2);
(3).
21.解下列方程组
(1)
(2)小明求得方程组的解为,由于不小心,滴上了墨水,刚好遮住了两个数和,求这两个数.
22.解下列方程组:
(1)
(2)
(3)
23.解下列方程组:
(1)
(2)
(3)
(4)
(5)
(6)
24.按要求解方程组
(1)(代入消元法)
(2)(加减消元法)
25.解下列二元一次方程组
(1)
(2)
(3)
(4)
26.解方程组:
(1);
(2).
27.解下列方程组
(1)
(2)
(3)
(4)
28.解下列方程组:
(1)
(2)
29.运用适当的方法解方程组:
(1)
(2)
30.解下列方程组:
(1)
(2)
《2025年中考数学专项突破练:解一元二次方程组》参考答案
1.
【分析】本题考查了解二元一次方程组,解题的关键是掌握二元一次方程组的解法.利用加减消元法求解即可.
【详解】解:
得:
,
将代入②得,,
原方程组的解为.
2.(1)
(2)
【分析】本题考查解二元一次方程组,掌握解二元一次方程组的方法正确计算是解题的关键.
(1)利用加减消元法解二元一次方程组即可;
(2)利用加减消元法解二元一次方程组即可.
【详解】(1)解:
①②,得
∴
把代入①,得 ,
解得:,
∴原方程组的解是:.
(2)解:方程组整理为
①②,得
∴
把代入①,得 ,
解得:,
∴原方程组的解为.
3.(1)
(2)
【分析】本题考查解二元一次方程组,掌握加减消元法是解题的关键.
(1)利用加减消法即可得解;
(2)先对第二个方程进行整理和变形,然后再利用加减消元法即可.
【详解】(1)解:,
由得:,
由得:,解得,
将代入①中得:,解得,
综上所述,方程组的解为.
(2)解:
由得:③,
由得:,解得,
将代入②中得:,解得,
综上所述,方程组的解为.
4.(1)
(2)
【分析】本题考查解二元一次方程,解题的关键在于熟练掌握加减消元法,代入消元法.
(1)利用加减消元法求解,即可解题;
(2)利用代入消元法求解,即可解题.
【详解】(1)解: ,
得:,
解得:,
将代入①中,得,
二元一次方程组解为;
(2)解:,
由①得:③,
将③带入②中,整理得:,
解得:,
将带入③中得:,
二元一次方程组解为.
5.(1)
(2)
【分析】本题考查了解二元一次方程组,熟练掌握解二元一次方程组的方法是解题的关键.
(1)运用加减消元法求解即可;
(2)运用加减消元法求解即可.
【详解】(1)解:
由得,,
解得:
将代入①得,,
解得:,
∴原方程组的解为:;
(2)解:
由得,,
解得:,
将代入①得,,
解得:,
∴原方程组的解为:.
6.(1)
(2)
【分析】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可.
【详解】(1)解:,
,得
,
∴,
把代入①,得
,
∴,
∴方程组的解为:.
(2)解:
,得
∴
把代入①,得
∴
∴方程组的解为:.
7.(1)
(2)
【分析】本题主要考查了解一元二次方程组,熟练掌握代入消元法和加减消元法是解题的关键.
(1)利用代入消元法进行求解即可;
(2)利用加减消元法进行求解即可.
【详解】(1)解:
将①代入②得,,
解得③,
将③代入①得,,
∴原二元一次方程组的解为;
(2)解:
得,③,
得,④,
得,,
解得,,
将代入①得,,
解得,,
∴原二元一次方程组的解为.
8.(1)
(2)
【分析】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可.
【详解】(1)解:得:
,
解得,
把代入①得:,
解得,
故原方程组的解是.
(2)解:得:
,
解得,
把代入①得:,
解得,
故原方程组的解是.
9.(1)
(2)
(3)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可;
(3)利用加减消元法求解即可.
【详解】(1)解:得:,即,
把代入①得:,
则方程组的解为;
(2)解:得:,即,
把代入①得:,
则方程组的解为;
(3)解:方程组整理得:,
两方程相加得:,即,
把代入第一个方程得:,
则方程组的解为.
10.(1)
(2)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)用加减消元法求解即可;
(2)先把方程组中的方程化为不含分母及括号的方程,再用加减消元法求解即可.
【详解】(1)解:把得,,
解得:,
把代入①得,,
解得:,
故此不等式组的解集为:;
(2)解:原方程组可化为,
得,,解得:,
把代入④得,,解得:,
故此方程组的解为.
11.(1)
(2)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可.
【详解】(1)解:,
得:,
解得:,
将代入①得:,解得:,
∴原方程组的解为.
(2)解:化简得,
由得:,
代入①得:,
∴.
∴原方程组的解为.
12.(1)
(2)
(3)
(4)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可;
(3)利用加减消元法求解即可;
(4)利用加减消元法求解即可.
【详解】(1)解:,
,得,解得:,
代入①得,解得:,
则方程组的解为;
(2)解:,
,得,解得:,
代入①,得,解得:,
则方程组的解为;
(3)解:
,得,解得:,
代入①,得,解得:,
则方程组的解为;
(4)解:方程组可化为,
,得,解得:,
代入②,得,解得:,
则方程组的解为.
13.(1)
(2)
【分析】本题主要考查了解二元一次方程组,熟知解二元一次方程组的方法是解题的关键.
(1)利用代入消元法解方程组即可;
(2)利用加减消元法解方程组即可.
【详解】(1)解:,
把①代入②得:,解得:,
把代入①得:,
∴原方程组的解为;
(2)解:,
得:,解得:,
把代入①得:,解得:,
∴原方程组的解为.
14.(1)
(2)
(3)
(4)
【分析】本题考查二元一次方程组的解法,涉及加减消元法及代入消元法,根据方程组的结构特征准确选择恰当消元法求解是解决问题的关键.
(1)利用代入消元法解二元一次方程组即可得到答案;
(2)先将方程组中两个方程的系数化相同,再利用加减消元法解二元一次方程组即可得到答案;
(3)利用加减消元法解二元一次方程组即可得到答案;
(4)先恒等变形化简,再将方程组中两个方程的系数化相同,最后利用加减消元法解二元一次方程组即可得到答案.
【详解】(1)解:,
将①代入②得,
解得,
将代入①得,
原方程组的解为;
(2)解:,
①②得,
将代入①得,
原方程组的解为;
(3)解:,
①②得,
将代入①得,
原方程组的解为;
(4)解:,
化简得,
②①得,
将代入②得,
原方程组的解为.
15.(1)
(2)
【分析】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.
(1)利用加减消元法即可求解;
(2)先将①两边乘以,得到③,然后利用加减消元法即可求解.
【详解】(1)解:
得,
解得:
将代入①得,
解得:
∴原方程组的解为:
(2)解:
由①得,③
得,
解得:
将代入②得,
解得:
∴原方程组的解为:
16.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,三元一次方程组的解法,掌握解法步骤是解本题的关键;
(1)由①②得:,再代入①得:,即可得到答案;
(2)先消去得到二元一次方程组,再解二元一次方程组,再进一步求解即可.
【详解】(1)解:,
①②得:,
解得:,
把代入①得:,
∴方程组的解为:;
(2)解:,
②③得:④,
④①得:,
把代入①得:,
把,代入③得:,
∴方程组的解为:;
17.(1)
(2)
【分析】本题考查了利用代入消元法和加减消元法解二元一次方程组的知识,掌握代入消元法和加减消元法是解答本题的关键.
(1)利用代入消元法即可求解;
(2)利用加减消元法即可求解.
【详解】(1)解: ,
把②代入①得:,
解得,
把代入②得:,
∴原方程组的解为;
(2)解:,
①②得:,
解得,
把代入①得:,
解得,
∴原方程组的解为.
18.(1)
(2)
【分析】(1)利用代入消元法解二元一次方程组即可.
(2)利用加减消元法解二元一次方程组即可.
本题考查了解二元一次方程组,熟练掌握其运算法则是解题的关键.
【详解】(1)解:
由①得.③.
把③代入②,得.
解得.
把代入③,得.
所以,方程组的解是 .
(2)原方程组整理得
方程①+②,得.
解得.
把代入①,得.
解得.
所以,方程组的解为.
19.(1)
(2)
【分析】本题考查解二元一次方程组,熟练掌握二元一次方程组的解法是解答的关键.
(1)利用加减消元法解方程组即可;
(2)利用代入消元法解方程组即可.
【详解】(1)解:原方程组为
由,得,解得,
把代入①,得,解得,
∴原方程组的解为;
(2)解:原方程组为
由①得:③ ,
把③代入②得:,解得:,
把代入③得:,
则方程组的解为.
20.(1)
(2)
(3)
【分析】本题主要考查解二元一次方程组,掌握代入消元法,加减消元法是关键.
(1)运用代入消元法计算即可;
(2)运用加减消元法计算即可;
(3)运用加减消元法计算即可.
【详解】(1)解:,
把①代入②得,,
整理得,,
解得,,
把代入①得,,
∴原方程组的解为;
(2)解:
将②式变形得,
∴,
①③得,,
解得,,
把代入①得,,
解得,,
∴原方程组的解为;
(3)解:,
①式去分母得,,
②式去分母,整理得,,
∴,
③④得,,
整理得,,
解得,,
把代入①得,,
解得,,
∴原方程组的解为.
21.(1)
(2)2和
【分析】本题考查解二元一次方程组和二元一次方程组的解,熟练掌握用加减消元法解方程组是解题的关键.
(1)利用加减消元法解方程组,由于两方程中的系数互为相反数,故应先用加减法求出的值,再用代入法求出的值.
(2)利用二元一次方程组解的意义,将代入方程中,求得值,再将值代入方程中,计算即可得出结论.
【详解】(1)解∶
得,,
解得,,
把代入①得,,
解得,,
故原方程组的解为;
(2)解:将代入方程得:,
解得:,
将代入方程中,
,
即两个数为2和.
22.(1)
(2)
(3)
【分析】本题考查解二元一次方程组,三元一次方程组:
(1)加减消元法解方程组即可;
(2)加减消元法解方程组即可;
(3)加减消元法解方程组即可.
【详解】(1)解:
,得:,解得:;
把代入①,得:,解得:;
∴方程组的解为:;
(2)原方程组可化为:
,得:,解得:,
把代入①,得:,解得:;
∴方程组的解为:;
(3)
,得:;
,得:;
,得:,解得:;
把代入③,得:,解得:;
把,代入③,得:,解得:;
∴方程组的解为:.
23.(1)
(2)
(3)
(4)
(5)
(6)
【分析】此题考查了解二元一次方程组和三元一次方程组,熟练掌握加减法和代入法是关键.
(1)利用代入法解方程组即可;
(2)利用加减法解方程组即可;
(3)利用加减法解方程组即可;
(4)利用加减法解方程组即可;
(5)利用加减法解方程组即可;
(6)利用加减法得到二元一次方程组,解得,,再求出即可.
【详解】(1)解:
把①代入②得,,
解得
把代入①得到,
∴
(2)解:
由①得,③
把③代入②得,,
解得
把代入③得到,
∴
(3)
②-①得,,
解得
把代入①得,,
解得
∴
(4)
①×③-②得,,
解得,
把代入①得,
解得
∴
(5)
①-②得,
∴
∴③
把③代入①得,,
解得
把代入③得,,
∴
(6)
①-②得,④
②+③得,⑤
得到,
把代入④得,
解得,
把,代入②得,,
解得
∴
24.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,掌握消元的方法是解本题的关键;
(1)把①化为,再代入②求解即可;
(2)由求解,再进一步求解即可.
【详解】(1)解:,
由①,得③,
把③代入②,得,
∴,
∴,
整理得:,
解得:,
把代入③,得,
所以原方程组的解是;
(2)解:,
,得,
解得:,
把代入①,得,
解得:,
所以原方程组的解是.
25.(1)
(2)
(3)
(4)
【分析】本题考查的是二元一次方程组的解法,掌握加减法解二元一次方程组是解题的关键.
(1)由的系数互为相反数,利用加法消去,求解,从而可得方程组的解;
(2)根据方程组的的系数特点,①②消去,求解,从而可得答案;
(3)根据方程组的的系数特点,②①消去,求解,从而可得答案;
(4)根据方程组的的系数特点,①②消去,求解,从而可得答案;
【详解】(1)解:
①+②得:
把代入①得:
方程组的解是:
(2)解:
①②得:
把代入①得:
方程组的解是:
(3)解:
②①得:
把代入②得:
方程组的解是:;
(4)解:
①得:③
②③得:
把代入①得:
方程组的解是:
26.(1);
(2).
【分析】本题考查了解二元一次方程组,根据题意灵活运用代入法或加减法是解题的关键.
(1)用代入法求解:直接把①代入②求得y的值,再代入①求得x的值,从而求解;
(2)用加减法求解:消去y,求得x的值,再求出y的值即可.
【详解】(1)解:把①代入②中,得,
解得.
把代入①中,得,
所以原方程组的解为;
(2)解:,得,解得.
将代入①中,得,解得,
所以原方程组的解为.
27.(1)
(2)
(3)
(4)
【分析】本题考查解二元一次方程组:
(1)代入消元法解方程组即可;
(2)加减消元法解方程组即可;
(3)加减消元法解方程组即可;
(4)加减消元法解方程组即可.
【详解】(1)解:
把代入,得:,解得:;
把代入②,得:;
∴方程组的解为:;
(2)
,得:,解得:;
把代入①,得:,解得:;
∴方程组的解为:;
(3),
,得:,解得;
把代入①,得:,解得:;
∴方程组的解为:;
(4)原方程组可化为:,
,得:,解得:;
把代入①,得:,解得:;
∴方程组的解为:.
28.(1)
(2)
【分析】本题考查了解二元一次方程组,掌握用代入消元法、加减消元法解二元一次方程组是解题的关键.
(1)整理方程组,然后用加减消元法即可解答;
(2)整理方程组,然后用加减消元法即可解答;
【详解】(1)解:
整理,得,
减去得,
即:,
解得:,
把代入③得,
解得:,
则方程组的解为:;
(2)解:
整理,得,
减去得,
即,
解得:,
把代入③得
解得:,
则方程组的解为:;
29.(1)
(2)
【分析】本题考查了解二元一次方程组,熟练掌握加减消元法解二元一次方程组是解此题的关键.
(1)先将方程组进行整理,再利用加减消元法计算即可得解;
(2)先将方程组进行整理,再利用加减消元法计算即可得解.
【详解】(1)解:方程组整理,得,
,得,
即.
将代入①,得,
即,
则方程组的解为;
(2)解:方程组整理,得
,得,
即.
将代入①,得,
则方程组的解为.
30.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,掌握解方程组的方法是解本题的关键;
(1)由先求解,再求解即可;
(2)把方程组整理为,再利用加减消元法解方程组即可.
【详解】(1)解: ,
,得,
即,
把代入①,得,
则方程组的解为.
(2)解:,
,得,
去分母,得.
去括号,合并同类项,得.
②去括号,得.
合并同类项,得.
联立方程组,得,
③④得:,
解得,
把代入③得:,
解得,
∴方程组的解为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年中考数学专项突破练:解一元二次方程组
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.解方程组:
2.解方程组:
(1)
(2)
3.解方程组:
(1)
(2)
4.解方程组:
(1);
(2).
5.解方程组:
(1)
(2)
6.解方程组:
(1) ;
(2).
7.解下列方程组
(1)
(2)
8.解方程组:
(1)
(2)
9.用加减法解下列方程组:
(1)
(2)
(3).
10.用加减法解下列方程组.
(1).
(2).
11.用加减法解下列方程组:
(1);
(2).
12.用加减法解下列方程组:
(1);
(2);
(3);
(4).
13.解下列方程组:
(1)
(2)
14.解下列方程组:
(1);
(2);
(3);
(4).
15.解二元一次方程组
(1)
(2)
16.解下列方程组:
(1)
(2)
17.解方程组:
(1)
(2)
18.解方程组:
(1)
(2)
19.解方程组:
(1)
(2)
20.解下列方程组:
(1);
(2);
(3).
21.解下列方程组
(1)
(2)小明求得方程组的解为,由于不小心,滴上了墨水,刚好遮住了两个数和,求这两个数.
22.解下列方程组:
(1)
(2)
(3)
23.解下列方程组:
(1)
(2)
(3)
(4)
(5)
(6)
24.按要求解方程组
(1)(代入消元法)
(2)(加减消元法)
25.解下列二元一次方程组
(1)
(2)
(3)
(4)
26.解方程组:
(1);
(2).
27.解下列方程组
(1)
(2)
(3)
(4)
28.解下列方程组:
(1)
(2)
29.运用适当的方法解方程组:
(1)
(2)
30.解下列方程组:
(1)
(2)
《2025年中考数学专项突破练:解一元二次方程组》参考答案
1.
【分析】本题考查了解二元一次方程组,解题的关键是掌握二元一次方程组的解法.利用加减消元法求解即可.
【详解】解:
得:
,
将代入②得,,
原方程组的解为.
2.(1)
(2)
【分析】本题考查解二元一次方程组,掌握解二元一次方程组的方法正确计算是解题的关键.
(1)利用加减消元法解二元一次方程组即可;
(2)利用加减消元法解二元一次方程组即可.
【详解】(1)解:
①②,得
∴
把代入①,得 ,
解得:,
∴原方程组的解是:.
(2)解:方程组整理为
①②,得
∴
把代入①,得 ,
解得:,
∴原方程组的解为.
3.(1)
(2)
【分析】本题考查解二元一次方程组,掌握加减消元法是解题的关键.
(1)利用加减消法即可得解;
(2)先对第二个方程进行整理和变形,然后再利用加减消元法即可.
【详解】(1)解:,
由得:,
由得:,解得,
将代入①中得:,解得,
综上所述,方程组的解为.
(2)解:
由得:③,
由得:,解得,
将代入②中得:,解得,
综上所述,方程组的解为.
4.(1)
(2)
【分析】本题考查解二元一次方程,解题的关键在于熟练掌握加减消元法,代入消元法.
(1)利用加减消元法求解,即可解题;
(2)利用代入消元法求解,即可解题.
【详解】(1)解: ,
得:,
解得:,
将代入①中,得,
二元一次方程组解为;
(2)解:,
由①得:③,
将③带入②中,整理得:,
解得:,
将带入③中得:,
二元一次方程组解为.
5.(1)
(2)
【分析】本题考查了解二元一次方程组,熟练掌握解二元一次方程组的方法是解题的关键.
(1)运用加减消元法求解即可;
(2)运用加减消元法求解即可.
【详解】(1)解:
由得,,
解得:
将代入①得,,
解得:,
∴原方程组的解为:;
(2)解:
由得,,
解得:,
将代入①得,,
解得:,
∴原方程组的解为:.
6.(1)
(2)
【分析】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可.
【详解】(1)解:,
,得
,
∴,
把代入①,得
,
∴,
∴方程组的解为:.
(2)解:
,得
∴
把代入①,得
∴
∴方程组的解为:.
7.(1)
(2)
【分析】本题主要考查了解一元二次方程组,熟练掌握代入消元法和加减消元法是解题的关键.
(1)利用代入消元法进行求解即可;
(2)利用加减消元法进行求解即可.
【详解】(1)解:
将①代入②得,,
解得③,
将③代入①得,,
∴原二元一次方程组的解为;
(2)解:
得,③,
得,④,
得,,
解得,,
将代入①得,,
解得,,
∴原二元一次方程组的解为.
8.(1)
(2)
【分析】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可.
【详解】(1)解:得:
,
解得,
把代入①得:,
解得,
故原方程组的解是.
(2)解:得:
,
解得,
把代入①得:,
解得,
故原方程组的解是.
9.(1)
(2)
(3)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可;
(3)利用加减消元法求解即可.
【详解】(1)解:得:,即,
把代入①得:,
则方程组的解为;
(2)解:得:,即,
把代入①得:,
则方程组的解为;
(3)解:方程组整理得:,
两方程相加得:,即,
把代入第一个方程得:,
则方程组的解为.
10.(1)
(2)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)用加减消元法求解即可;
(2)先把方程组中的方程化为不含分母及括号的方程,再用加减消元法求解即可.
【详解】(1)解:把得,,
解得:,
把代入①得,,
解得:,
故此不等式组的解集为:;
(2)解:原方程组可化为,
得,,解得:,
把代入④得,,解得:,
故此方程组的解为.
11.(1)
(2)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可.
【详解】(1)解:,
得:,
解得:,
将代入①得:,解得:,
∴原方程组的解为.
(2)解:化简得,
由得:,
代入①得:,
∴.
∴原方程组的解为.
12.(1)
(2)
(3)
(4)
【分析】本题考查了解二元一次方程组,掌握加减消元法是解此题的关键.
(1)利用加减消元法求解即可;
(2)利用加减消元法求解即可;
(3)利用加减消元法求解即可;
(4)利用加减消元法求解即可.
【详解】(1)解:,
,得,解得:,
代入①得,解得:,
则方程组的解为;
(2)解:,
,得,解得:,
代入①,得,解得:,
则方程组的解为;
(3)解:
,得,解得:,
代入①,得,解得:,
则方程组的解为;
(4)解:方程组可化为,
,得,解得:,
代入②,得,解得:,
则方程组的解为.
13.(1)
(2)
【分析】本题主要考查了解二元一次方程组,熟知解二元一次方程组的方法是解题的关键.
(1)利用代入消元法解方程组即可;
(2)利用加减消元法解方程组即可.
【详解】(1)解:,
把①代入②得:,解得:,
把代入①得:,
∴原方程组的解为;
(2)解:,
得:,解得:,
把代入①得:,解得:,
∴原方程组的解为.
14.(1)
(2)
(3)
(4)
【分析】本题考查二元一次方程组的解法,涉及加减消元法及代入消元法,根据方程组的结构特征准确选择恰当消元法求解是解决问题的关键.
(1)利用代入消元法解二元一次方程组即可得到答案;
(2)先将方程组中两个方程的系数化相同,再利用加减消元法解二元一次方程组即可得到答案;
(3)利用加减消元法解二元一次方程组即可得到答案;
(4)先恒等变形化简,再将方程组中两个方程的系数化相同,最后利用加减消元法解二元一次方程组即可得到答案.
【详解】(1)解:,
将①代入②得,
解得,
将代入①得,
原方程组的解为;
(2)解:,
①②得,
将代入①得,
原方程组的解为;
(3)解:,
①②得,
将代入①得,
原方程组的解为;
(4)解:,
化简得,
②①得,
将代入②得,
原方程组的解为.
15.(1)
(2)
【分析】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.
(1)利用加减消元法即可求解;
(2)先将①两边乘以,得到③,然后利用加减消元法即可求解.
【详解】(1)解:
得,
解得:
将代入①得,
解得:
∴原方程组的解为:
(2)解:
由①得,③
得,
解得:
将代入②得,
解得:
∴原方程组的解为:
16.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,三元一次方程组的解法,掌握解法步骤是解本题的关键;
(1)由①②得:,再代入①得:,即可得到答案;
(2)先消去得到二元一次方程组,再解二元一次方程组,再进一步求解即可.
【详解】(1)解:,
①②得:,
解得:,
把代入①得:,
∴方程组的解为:;
(2)解:,
②③得:④,
④①得:,
把代入①得:,
把,代入③得:,
∴方程组的解为:;
17.(1)
(2)
【分析】本题考查了利用代入消元法和加减消元法解二元一次方程组的知识,掌握代入消元法和加减消元法是解答本题的关键.
(1)利用代入消元法即可求解;
(2)利用加减消元法即可求解.
【详解】(1)解: ,
把②代入①得:,
解得,
把代入②得:,
∴原方程组的解为;
(2)解:,
①②得:,
解得,
把代入①得:,
解得,
∴原方程组的解为.
18.(1)
(2)
【分析】(1)利用代入消元法解二元一次方程组即可.
(2)利用加减消元法解二元一次方程组即可.
本题考查了解二元一次方程组,熟练掌握其运算法则是解题的关键.
【详解】(1)解:
由①得.③.
把③代入②,得.
解得.
把代入③,得.
所以,方程组的解是 .
(2)原方程组整理得
方程①+②,得.
解得.
把代入①,得.
解得.
所以,方程组的解为.
19.(1)
(2)
【分析】本题考查解二元一次方程组,熟练掌握二元一次方程组的解法是解答的关键.
(1)利用加减消元法解方程组即可;
(2)利用代入消元法解方程组即可.
【详解】(1)解:原方程组为
由,得,解得,
把代入①,得,解得,
∴原方程组的解为;
(2)解:原方程组为
由①得:③ ,
把③代入②得:,解得:,
把代入③得:,
则方程组的解为.
20.(1)
(2)
(3)
【分析】本题主要考查解二元一次方程组,掌握代入消元法,加减消元法是关键.
(1)运用代入消元法计算即可;
(2)运用加减消元法计算即可;
(3)运用加减消元法计算即可.
【详解】(1)解:,
把①代入②得,,
整理得,,
解得,,
把代入①得,,
∴原方程组的解为;
(2)解:
将②式变形得,
∴,
①③得,,
解得,,
把代入①得,,
解得,,
∴原方程组的解为;
(3)解:,
①式去分母得,,
②式去分母,整理得,,
∴,
③④得,,
整理得,,
解得,,
把代入①得,,
解得,,
∴原方程组的解为.
21.(1)
(2)2和
【分析】本题考查解二元一次方程组和二元一次方程组的解,熟练掌握用加减消元法解方程组是解题的关键.
(1)利用加减消元法解方程组,由于两方程中的系数互为相反数,故应先用加减法求出的值,再用代入法求出的值.
(2)利用二元一次方程组解的意义,将代入方程中,求得值,再将值代入方程中,计算即可得出结论.
【详解】(1)解∶
得,,
解得,,
把代入①得,,
解得,,
故原方程组的解为;
(2)解:将代入方程得:,
解得:,
将代入方程中,
,
即两个数为2和.
22.(1)
(2)
(3)
【分析】本题考查解二元一次方程组,三元一次方程组:
(1)加减消元法解方程组即可;
(2)加减消元法解方程组即可;
(3)加减消元法解方程组即可.
【详解】(1)解:
,得:,解得:;
把代入①,得:,解得:;
∴方程组的解为:;
(2)原方程组可化为:
,得:,解得:,
把代入①,得:,解得:;
∴方程组的解为:;
(3)
,得:;
,得:;
,得:,解得:;
把代入③,得:,解得:;
把,代入③,得:,解得:;
∴方程组的解为:.
23.(1)
(2)
(3)
(4)
(5)
(6)
【分析】此题考查了解二元一次方程组和三元一次方程组,熟练掌握加减法和代入法是关键.
(1)利用代入法解方程组即可;
(2)利用加减法解方程组即可;
(3)利用加减法解方程组即可;
(4)利用加减法解方程组即可;
(5)利用加减法解方程组即可;
(6)利用加减法得到二元一次方程组,解得,,再求出即可.
【详解】(1)解:
把①代入②得,,
解得
把代入①得到,
∴
(2)解:
由①得,③
把③代入②得,,
解得
把代入③得到,
∴
(3)
②-①得,,
解得
把代入①得,,
解得
∴
(4)
①×③-②得,,
解得,
把代入①得,
解得
∴
(5)
①-②得,
∴
∴③
把③代入①得,,
解得
把代入③得,,
∴
(6)
①-②得,④
②+③得,⑤
得到,
把代入④得,
解得,
把,代入②得,,
解得
∴
24.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,掌握消元的方法是解本题的关键;
(1)把①化为,再代入②求解即可;
(2)由求解,再进一步求解即可.
【详解】(1)解:,
由①,得③,
把③代入②,得,
∴,
∴,
整理得:,
解得:,
把代入③,得,
所以原方程组的解是;
(2)解:,
,得,
解得:,
把代入①,得,
解得:,
所以原方程组的解是.
25.(1)
(2)
(3)
(4)
【分析】本题考查的是二元一次方程组的解法,掌握加减法解二元一次方程组是解题的关键.
(1)由的系数互为相反数,利用加法消去,求解,从而可得方程组的解;
(2)根据方程组的的系数特点,①②消去,求解,从而可得答案;
(3)根据方程组的的系数特点,②①消去,求解,从而可得答案;
(4)根据方程组的的系数特点,①②消去,求解,从而可得答案;
【详解】(1)解:
①+②得:
把代入①得:
方程组的解是:
(2)解:
①②得:
把代入①得:
方程组的解是:
(3)解:
②①得:
把代入②得:
方程组的解是:;
(4)解:
①得:③
②③得:
把代入①得:
方程组的解是:
26.(1);
(2).
【分析】本题考查了解二元一次方程组,根据题意灵活运用代入法或加减法是解题的关键.
(1)用代入法求解:直接把①代入②求得y的值,再代入①求得x的值,从而求解;
(2)用加减法求解:消去y,求得x的值,再求出y的值即可.
【详解】(1)解:把①代入②中,得,
解得.
把代入①中,得,
所以原方程组的解为;
(2)解:,得,解得.
将代入①中,得,解得,
所以原方程组的解为.
27.(1)
(2)
(3)
(4)
【分析】本题考查解二元一次方程组:
(1)代入消元法解方程组即可;
(2)加减消元法解方程组即可;
(3)加减消元法解方程组即可;
(4)加减消元法解方程组即可.
【详解】(1)解:
把代入,得:,解得:;
把代入②,得:;
∴方程组的解为:;
(2)
,得:,解得:;
把代入①,得:,解得:;
∴方程组的解为:;
(3),
,得:,解得;
把代入①,得:,解得:;
∴方程组的解为:;
(4)原方程组可化为:,
,得:,解得:;
把代入①,得:,解得:;
∴方程组的解为:.
28.(1)
(2)
【分析】本题考查了解二元一次方程组,掌握用代入消元法、加减消元法解二元一次方程组是解题的关键.
(1)整理方程组,然后用加减消元法即可解答;
(2)整理方程组,然后用加减消元法即可解答;
【详解】(1)解:
整理,得,
减去得,
即:,
解得:,
把代入③得,
解得:,
则方程组的解为:;
(2)解:
整理,得,
减去得,
即,
解得:,
把代入③得
解得:,
则方程组的解为:;
29.(1)
(2)
【分析】本题考查了解二元一次方程组,熟练掌握加减消元法解二元一次方程组是解此题的关键.
(1)先将方程组进行整理,再利用加减消元法计算即可得解;
(2)先将方程组进行整理,再利用加减消元法计算即可得解.
【详解】(1)解:方程组整理,得,
,得,
即.
将代入①,得,
即,
则方程组的解为;
(2)解:方程组整理,得
,得,
即.
将代入①,得,
则方程组的解为.
30.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,掌握解方程组的方法是解本题的关键;
(1)由先求解,再求解即可;
(2)把方程组整理为,再利用加减消元法解方程组即可.
【详解】(1)解: ,
,得,
即,
把代入①,得,
则方程组的解为.
(2)解:,
,得,
去分母,得.
去括号,合并同类项,得.
②去括号,得.
合并同类项,得.
联立方程组,得,
③④得:,
解得,
把代入③得:,
解得,
∴方程组的解为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
