8.1.1 向量数量积的概念 课件(共22张PPT)2024-2025学年高一数学人教B版(2019)必修3
文档属性
| 名称 | 8.1.1 向量数量积的概念 课件(共22张PPT)2024-2025学年高一数学人教B版(2019)必修3 |
|
|
| 格式 | pptx | ||
| 文件大小 | 702.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 15:19:19 | ||
图片预览




文档简介
(共22张PPT)
8.1.1 向量数量积的概念
人教B版(2019)必修第三册
1.理解平面向量数量积的概念,会求平面向量的数量积.
2.理解投影向量及投影数量的概念.
3.理解平面向量数量积的几何意义.
问题:如果一个物体在力F作用下产生位移s,那么F所做的功是多少?
W=|F||s|
F
s
图1
F
s
图2
F
θ
F
θ
W=|F||s|cos θ
思考:功与向量的数量积有什么联系?
物理上力做功实质是力在物体前进方向上的分力与物体位移的乘积,
它的实质是向量的数量积.
已知两个非零向量a、b,在平面内任取一点O,作 =a, =b,则称[0,π]内的∠AOB为向量a和向量b的夹角,记作.
a
b
O
A
a
B
b
2.∈[0,π];
4.两个向量的夹角是唯一确定的.
注意:1.两个向量移至共起点;
3.=;
O
A
a
B
b
θ
O
A
B
b
a
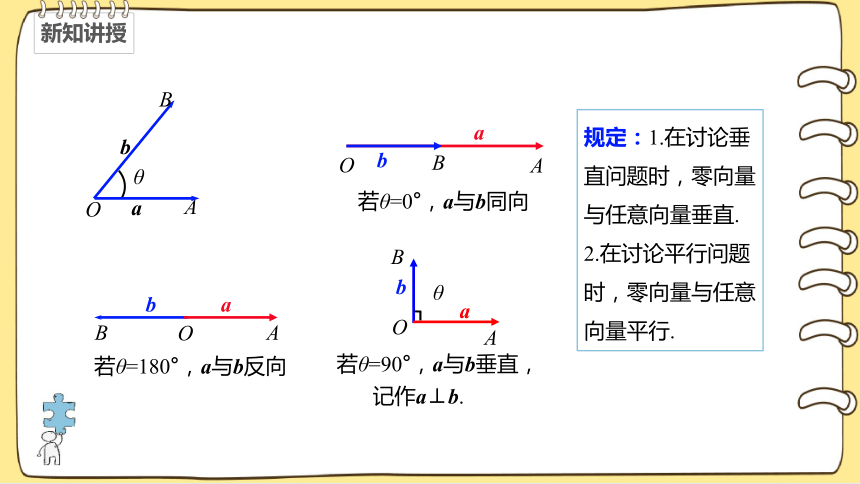
若θ=0°,a与b同向
O
A
B
b
a
若θ=180°,a与b反向
O
A
B
a
b
若θ=90°,a与b垂直,
记作a⊥b.
θ
规定:1.在讨论垂直问题时,零向量与任意向量垂直.
2.在讨论平行问题时,零向量与任意向量平行.
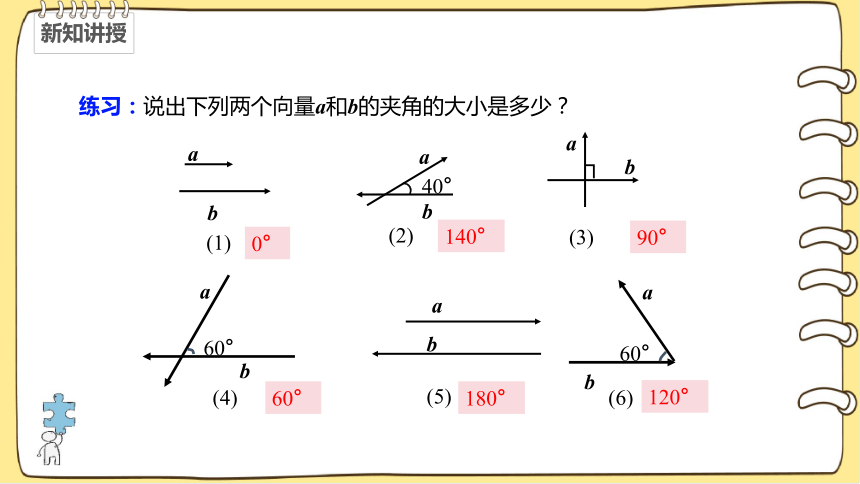
练习:说出下列两个向量a和b的夹角的大小是多少?
(1)
b
a
40°
╮
(2)
a
b
60°
(4)
a
b
(3)
┐
a
b
60°
(6)
b
a
(5)
b
a
0°
140°
90°
120°
180°
60°
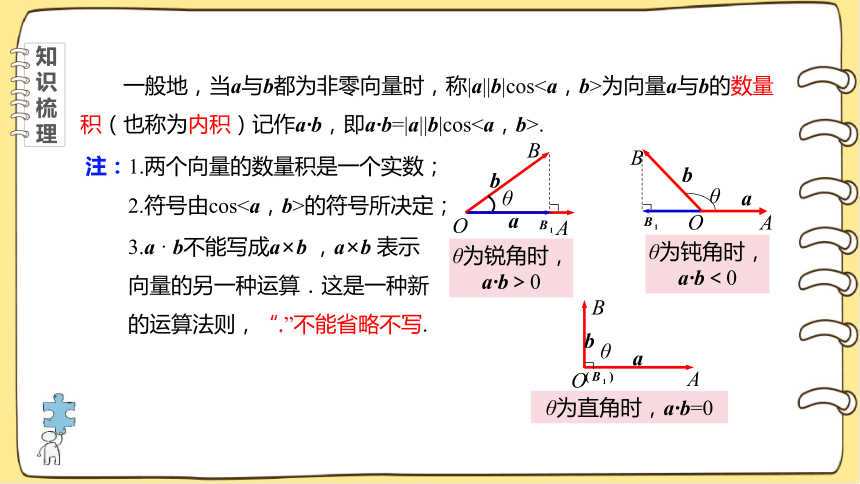
一般地,当a与b都为非零向量时,称|a||b|cos为向量a与b的数量积(也称为内积)记作a·b,即a·b=|a||b|cos.
注:1.两个向量的数量积是一个实数;
2.符号由cos的符号所决定;
O
A
B
a
b
θ
B
O
A
a
b
θ
O
A
B
a
b
θ
θ为锐角时,
a·b>0
θ为钝角时,
a·b<0
θ为直角时,a·b=0
3.a · b不能写成a×b ,a×b 表示
向量的另一种运算.这是一种新的运算法则,“.”不能省略不写.
向量数量积的性质
1.a2=a·a=|a|2或|a|= ;
2.cos= ;
3.a⊥b a·b=0.
用于计算向量的模
用于计算向量的夹角,以及判断三角形的形状
内积为零是判定两向量垂直的条件
4.|a·b|≤|a||b|.
证明:|a·b|=||a||b|cos|=|a||b||cos|,
∵∈[0,π],∴cos∈[-1,1],
∴|cos|∈[0,1],
∴|a·b|≤|a||b|.
例1 在边长为a的正六边形ABCDEF中,试求:
设非零向量 =a,过A,B分别做直线l的垂线,垂足分别为A1,B1,则称向量 为向量a在直线l上的投影向量或投影.
给定平面上的一个非零向量b,设b所在直线为l,则a在直线l上的投影称为a在向量b上的投影.
a
A
B
A1
B1
l
B
a
A
A1
B1
l
b
问题:向量 的方向和长度与有什么关联?
A1
B1
a
b
θ
A1
B1
b
a
θ
A1(B1)
a
b
θ
为锐角时,
=|a|cos>0
为钝角时,
=|a|cos<0
θ为直角时,
如果a,b为两个非零向量,则称|a|cos为向量a在向量b上的投影的数量.
O
A
B
b
a
θ
|a|cos θ
a·b=|a||b|cos=(|a|cos)|b|
向量数量积的几何意义:
两个非零向量a,b的数量积a·b,等于a在向量b上的投影的数量与b的模的乘积.
延伸1:向量a在向量b上的投影的数量|a|cos= .
延伸2:当e为单位向量,a·e=|a|cos.
向量投影的数量的求法
即任意向量与单位向量的数量积,等于这个向量在单位向量e上的投影.
思考1:一个向量在一个非零向量上的投影,与这个非零向量共线吗?若共线,它们的方向相同还是相反?
一个向量在一个非零向量上的投影,一定与这个非零向量共线,但它们既有可能方向相同,也有可能方向相反.
思考2:向量b在向量a上的投影的数量与向量a在向量b上的投影的数量相同吗?
向量b在向量a上的投影的数量 |b|cos〈a,b〉
向量a在向量b上的投影的数量 |a|cos〈a,b〉
不相同
例2 (多选题)已知a,b,c是三个非零向量,下列选项正确的是( )
A.|a·b|=|a|·|b| a∥b
B.a,b反向 a·b=-|a||b|
C.a⊥b |a+b|=|a-b|
D.|a|=|b| |a·c|=|b·c|
解析:|a·b|=|a|·|b|·|cos θ|=|a|·|b| |cos θ|=1 cos θ=±1 θ=0或π a∥b
a,b反向 θ=π cos θ=-1 a·b=-|a||b|
a⊥b a·b=0 |a+b|2=|a-b|2 |a+b|=|a-b|
若|a|=|b|,则〈a,c〉与〈b,c〉不一定相等,故|a·c|=|b·c|不成立,
当|a·c|=|b·c|时,只能说明a,b在c上的投影相等,但|a|=|b|不一定成立.
ABC
例3 如图所示,求出以下向量的数量积.
(1)b·a; (2)c·a; (3)d·a.
解:(1)(方法一)由图可知:|a|=1,|b|= ,= ,因此b·a=1.
(方法二)由图可知:向量b在向量a上投影的数量为1,且a为单位向量,
因此根据向量数量积的几何意义可知b·a=1.
(2)由图可知:= ,因此c·a=0.
(3)由图可知:向量d在向量a上投影的数量为-1,且a为单位向量,
因此根据向量数量积的几何意义可知d·a=-1.
例4 在△ABC中, 求:
① ;② 在 方向上的投影的数量.
解:∵ ∴△ABC是直角三角形,且∠C=90°,
①
②
1.已知|a|=3,|b|=4,且a与b的夹角θ=150°,则a·b等于( )
A.-6 B.6 C.-6 D.6
2.已知|a|=9,|b|=6,a·b=-54,则a与b的夹角θ为( )
A.45° B.135° C.120° D.150°
C
B
3.已知|a|=6,|b|=3,〈a,b〉=150°,则向量b在a上的投影的数量为( )
A.2 B.-2 C. D.-
D
45°
根据今天所学,回答下列问题:
(1)平面向量数量积的含义是什么?
(2)如何判断两个向量是否垂直?
(3)如何利用向量数量积的几何意义,求解向量的数量积?
8.1.1 向量数量积的概念
人教B版(2019)必修第三册
1.理解平面向量数量积的概念,会求平面向量的数量积.
2.理解投影向量及投影数量的概念.
3.理解平面向量数量积的几何意义.
问题:如果一个物体在力F作用下产生位移s,那么F所做的功是多少?
W=|F||s|
F
s
图1
F
s
图2
F
θ
F
θ
W=|F||s|cos θ
思考:功与向量的数量积有什么联系?
物理上力做功实质是力在物体前进方向上的分力与物体位移的乘积,
它的实质是向量的数量积.
已知两个非零向量a、b,在平面内任取一点O,作 =a, =b,则称[0,π]内的∠AOB为向量a和向量b的夹角,记作
a
b
O
A
a
B
b
2.
4.两个向量的夹角是唯一确定的.
注意:1.两个向量移至共起点;
3.
O
A
a
B
b
θ
O
A
B
b
a
若θ=0°,a与b同向
O
A
B
b
a
若θ=180°,a与b反向
O
A
B
a
b
若θ=90°,a与b垂直,
记作a⊥b.
θ
规定:1.在讨论垂直问题时,零向量与任意向量垂直.
2.在讨论平行问题时,零向量与任意向量平行.
练习:说出下列两个向量a和b的夹角的大小是多少?
(1)
b
a
40°
╮
(2)
a
b
60°
(4)
a
b
(3)
┐
a
b
60°
(6)
b
a
(5)
b
a
0°
140°
90°
120°
180°
60°
一般地,当a与b都为非零向量时,称|a||b|cos
注:1.两个向量的数量积是一个实数;
2.符号由cos
O
A
B
a
b
θ
B
O
A
a
b
θ
O
A
B
a
b
θ
θ为锐角时,
a·b>0
θ为钝角时,
a·b<0
θ为直角时,a·b=0
3.a · b不能写成a×b ,a×b 表示
向量的另一种运算.这是一种新的运算法则,“.”不能省略不写.
向量数量积的性质
1.a2=a·a=|a|2或|a|= ;
2.cos
3.a⊥b a·b=0.
用于计算向量的模
用于计算向量的夹角,以及判断三角形的形状
内积为零是判定两向量垂直的条件
4.|a·b|≤|a||b|.
证明:|a·b|=||a||b|cos
∵
∴|cos
∴|a·b|≤|a||b|.
例1 在边长为a的正六边形ABCDEF中,试求:
设非零向量 =a,过A,B分别做直线l的垂线,垂足分别为A1,B1,则称向量 为向量a在直线l上的投影向量或投影.
给定平面上的一个非零向量b,设b所在直线为l,则a在直线l上的投影称为a在向量b上的投影.
a
A
B
A1
B1
l
B
a
A
A1
B1
l
b
问题:向量 的方向和长度与
A1
B1
a
b
θ
A1
B1
b
a
θ
A1(B1)
a
b
θ
=|a|cos
=|a|cos
θ为直角时,
如果a,b为两个非零向量,则称|a|cos
O
A
B
b
a
θ
|a|cos θ
a·b=|a||b|cos
向量数量积的几何意义:
两个非零向量a,b的数量积a·b,等于a在向量b上的投影的数量与b的模的乘积.
延伸1:向量a在向量b上的投影的数量|a|cos
延伸2:当e为单位向量,a·e=|a|cos
向量投影的数量的求法
即任意向量与单位向量的数量积,等于这个向量在单位向量e上的投影.
思考1:一个向量在一个非零向量上的投影,与这个非零向量共线吗?若共线,它们的方向相同还是相反?
一个向量在一个非零向量上的投影,一定与这个非零向量共线,但它们既有可能方向相同,也有可能方向相反.
思考2:向量b在向量a上的投影的数量与向量a在向量b上的投影的数量相同吗?
向量b在向量a上的投影的数量 |b|cos〈a,b〉
向量a在向量b上的投影的数量 |a|cos〈a,b〉
不相同
例2 (多选题)已知a,b,c是三个非零向量,下列选项正确的是( )
A.|a·b|=|a|·|b| a∥b
B.a,b反向 a·b=-|a||b|
C.a⊥b |a+b|=|a-b|
D.|a|=|b| |a·c|=|b·c|
解析:|a·b|=|a|·|b|·|cos θ|=|a|·|b| |cos θ|=1 cos θ=±1 θ=0或π a∥b
a,b反向 θ=π cos θ=-1 a·b=-|a||b|
a⊥b a·b=0 |a+b|2=|a-b|2 |a+b|=|a-b|
若|a|=|b|,则〈a,c〉与〈b,c〉不一定相等,故|a·c|=|b·c|不成立,
当|a·c|=|b·c|时,只能说明a,b在c上的投影相等,但|a|=|b|不一定成立.
ABC
例3 如图所示,求出以下向量的数量积.
(1)b·a; (2)c·a; (3)d·a.
解:(1)(方法一)由图可知:|a|=1,|b|= ,
(方法二)由图可知:向量b在向量a上投影的数量为1,且a为单位向量,
因此根据向量数量积的几何意义可知b·a=1.
(2)由图可知:
(3)由图可知:向量d在向量a上投影的数量为-1,且a为单位向量,
因此根据向量数量积的几何意义可知d·a=-1.
例4 在△ABC中, 求:
① ;② 在 方向上的投影的数量.
解:∵ ∴△ABC是直角三角形,且∠C=90°,
①
②
1.已知|a|=3,|b|=4,且a与b的夹角θ=150°,则a·b等于( )
A.-6 B.6 C.-6 D.6
2.已知|a|=9,|b|=6,a·b=-54,则a与b的夹角θ为( )
A.45° B.135° C.120° D.150°
C
B
3.已知|a|=6,|b|=3,〈a,b〉=150°,则向量b在a上的投影的数量为( )
A.2 B.-2 C. D.-
D
45°
根据今天所学,回答下列问题:
(1)平面向量数量积的含义是什么?
(2)如何判断两个向量是否垂直?
(3)如何利用向量数量积的几何意义,求解向量的数量积?
