8.1.2 向量数量积的运算律 课件(共16张PPT)2024-2025学年高一数学人教B版(2019)必修3
文档属性
| 名称 | 8.1.2 向量数量积的运算律 课件(共16张PPT)2024-2025学年高一数学人教B版(2019)必修3 |
|
|
| 格式 | pptx | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
8.1.2 向量数量积的运算律
人教B版(2019)必修第三册
1.掌握向量数量积的运算律.
2.能根据运算律解决一些向量数量积的运算问题.
问题:实数乘法有哪些运算律?结合向量的线性运算的运算律,猜想向量数量积的运算律.
①
③
②
实数乘法
猜想
①a·b=b·a;
③(a+b)·c=a·c+b·c.
②(ab)·c=a·(bc);
向量数量积
向量数量积的运算律的猜想、证明:
猜想①:当a,b是两个非零向量时,因为 = ,所以根据 a·b = |a| |b| cos ,b·a= |b| |a| cos 可知:
即向量数量积满足交换律,猜想①成立!
a·b =b·a
m
n
猜想 ②:
但 与 a 不一定是共线的,故猜想 ② 不成立!
思考:三个向量不满足结合律,那么两个向量和一个实数相乘是否满足结合律呢?
(1)当,中至少有一个是零向量或λ = 0时: (λ)·= λ() ;
两个向量和一个实数相乘:
猜想 (λ)·= λ(·)
综上所述,猜想成立,即两个向量和一个实数相乘满足结合律.
(2)若 λ > 0:则|λ| = λ||,且 λ的方向与的方向相同,从而
<,> = <,>,
因此 (λ)·= |λ|·|| cos <,> = λ||·|| cos <,> = λ(·);
(3)若 λ < 0:则|λ| = – λ||,且 λ的方向与的方向相反,从而
<,> = π – <,>,
因此 (λ)·= |λ|·|| cos <,> = – λ||·|| cos(π – <,>) = λ(·).
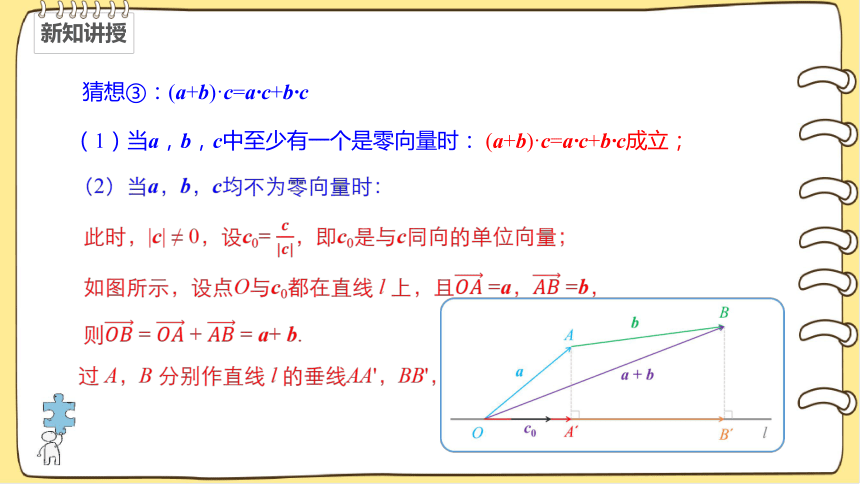
猜想③:(a+b)·c=a·c+b·c
(1)当a,b,c中至少有一个是零向量时: (a+b)·c=a·c+b·c成立;
(2)当a,b,c均不为零向量时:
此时,|c| ≠ 0,设c0= ,即c0是与c同向的单位向量;
如图所示,设点O与c0都在直线 l 上,且 =a, =b,
则 = + = a+ b.
过 A,B 分别作直线 l 的垂线AA',BB',
由向量投影的定义可知,a在c0上的投影为,b在c0上的投影为,
a+b在c0上的投影为;
又因为 = + ,
所以根据向量数量积的几何意义可知
(a+b)·c0= a·c0+b·c0,
式子两边同时乘以 |c|,即可知
(a+b)·c=a·c+b·c,即向量数量积对加法满足分配律;
同理可证:a·(b+c)=a·b+a·c,(a-b)·c=a·c-b·c.
b
a
A
B
O
A
a + b
B
c0
l
对于向量a,b,c和实数 λ,有:
向量数量积的运算律
(1)a·b =b·a;
(2)(λa)·b = λ(a·b);
(3)(a±b)·c=a·c±b·c.
思考:“若a·b=a·c,则b=c”成立吗?为什么?
不成立,如a⊥b,a⊥c时,a·b=a·c,但b与c不一定相等.
例1 已知a与b的夹角θ=150°,且|a|=3,|b|=4,求:
(1)(a+b)·(a-2b);(2)|a+2b|.
解:(1)(a+b)·(a-2b)=a2-a·b-2b2
=|a|2-|a||b|cos θ-2|b|2
=32-3×4×cos 150°-2×42
=-23+6.
(2)∵|a+2b|2=a2+4a·b+4b2
=32+4×3×4×cos 150°+4×42
=73-24,
∴|a+2b|=.
例2 已知a⊥b,|a|=2,|b|=3且向量3a+2b与ka-b互相垂直,求k的值.
解:∵3a+2b与ka-b互相垂直,
∴(3a+2b)·(ka-b)=0,
∴3ka2+(2k-3)a·b-2b2=0.
∵a⊥b,∴a·b=0,
又|a|=2,|b|=3,∴12k-18=0,k=.
例3 求证:平行四边形两条对角线的平方和等于四条边的平方和.
1.下列说法正确的是( )
A.|a·b|=|a||b|
B.a·b≠0 |a|+|b|≠0
C.a·b=0 |a||b|=0
D.(a+b)·c=a·c+b·c
2.若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为( )
A.30° B.60° C.120° D.150°
D
C
3.已知向量a、b的夹角为60°,|a|=|b|=1,且向量a与λb-a垂直,则实数λ=________.
4.设向量a,b满足|a+b|=,|a-b|=,则a·b=________.
2
1
向量数量积的运算律
交换律
结合律
分配律
a·b =b·a
(λa)·b = λ(a·b)
(a±b)·c=a·c±b·c
8.1.2 向量数量积的运算律
人教B版(2019)必修第三册
1.掌握向量数量积的运算律.
2.能根据运算律解决一些向量数量积的运算问题.
问题:实数乘法有哪些运算律?结合向量的线性运算的运算律,猜想向量数量积的运算律.
①
③
②
实数乘法
猜想
①a·b=b·a;
③(a+b)·c=a·c+b·c.
②(ab)·c=a·(bc);
向量数量积
向量数量积的运算律的猜想、证明:
猜想①:当a,b是两个非零向量时,因为
即向量数量积满足交换律,猜想①成立!
a·b =b·a
m
n
猜想 ②:
但 与 a 不一定是共线的,故猜想 ② 不成立!
思考:三个向量不满足结合律,那么两个向量和一个实数相乘是否满足结合律呢?
(1)当,中至少有一个是零向量或λ = 0时: (λ)·= λ() ;
两个向量和一个实数相乘:
猜想 (λ)·= λ(·)
综上所述,猜想成立,即两个向量和一个实数相乘满足结合律.
(2)若 λ > 0:则|λ| = λ||,且 λ的方向与的方向相同,从而
<,> = <,>,
因此 (λ)·= |λ|·|| cos <,> = λ||·|| cos <,> = λ(·);
(3)若 λ < 0:则|λ| = – λ||,且 λ的方向与的方向相反,从而
<,> = π – <,>,
因此 (λ)·= |λ|·|| cos <,> = – λ||·|| cos(π – <,>) = λ(·).
猜想③:(a+b)·c=a·c+b·c
(1)当a,b,c中至少有一个是零向量时: (a+b)·c=a·c+b·c成立;
(2)当a,b,c均不为零向量时:
此时,|c| ≠ 0,设c0= ,即c0是与c同向的单位向量;
如图所示,设点O与c0都在直线 l 上,且 =a, =b,
则 = + = a+ b.
过 A,B 分别作直线 l 的垂线AA',BB',
由向量投影的定义可知,a在c0上的投影为,b在c0上的投影为,
a+b在c0上的投影为;
又因为 = + ,
所以根据向量数量积的几何意义可知
(a+b)·c0= a·c0+b·c0,
式子两边同时乘以 |c|,即可知
(a+b)·c=a·c+b·c,即向量数量积对加法满足分配律;
同理可证:a·(b+c)=a·b+a·c,(a-b)·c=a·c-b·c.
b
a
A
B
O
A
a + b
B
c0
l
对于向量a,b,c和实数 λ,有:
向量数量积的运算律
(1)a·b =b·a;
(2)(λa)·b = λ(a·b);
(3)(a±b)·c=a·c±b·c.
思考:“若a·b=a·c,则b=c”成立吗?为什么?
不成立,如a⊥b,a⊥c时,a·b=a·c,但b与c不一定相等.
例1 已知a与b的夹角θ=150°,且|a|=3,|b|=4,求:
(1)(a+b)·(a-2b);(2)|a+2b|.
解:(1)(a+b)·(a-2b)=a2-a·b-2b2
=|a|2-|a||b|cos θ-2|b|2
=32-3×4×cos 150°-2×42
=-23+6.
(2)∵|a+2b|2=a2+4a·b+4b2
=32+4×3×4×cos 150°+4×42
=73-24,
∴|a+2b|=.
例2 已知a⊥b,|a|=2,|b|=3且向量3a+2b与ka-b互相垂直,求k的值.
解:∵3a+2b与ka-b互相垂直,
∴(3a+2b)·(ka-b)=0,
∴3ka2+(2k-3)a·b-2b2=0.
∵a⊥b,∴a·b=0,
又|a|=2,|b|=3,∴12k-18=0,k=.
例3 求证:平行四边形两条对角线的平方和等于四条边的平方和.
1.下列说法正确的是( )
A.|a·b|=|a||b|
B.a·b≠0 |a|+|b|≠0
C.a·b=0 |a||b|=0
D.(a+b)·c=a·c+b·c
2.若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为( )
A.30° B.60° C.120° D.150°
D
C
3.已知向量a、b的夹角为60°,|a|=|b|=1,且向量a与λb-a垂直,则实数λ=________.
4.设向量a,b满足|a+b|=,|a-b|=,则a·b=________.
2
1
向量数量积的运算律
交换律
结合律
分配律
a·b =b·a
(λa)·b = λ(a·b)
(a±b)·c=a·c±b·c
