8.2.4 三角恒等变换的应用 课件(共19张PPT)2024-2025学年高一数学人教B版(2019)必修3
文档属性
| 名称 | 8.2.4 三角恒等变换的应用 课件(共19张PPT)2024-2025学年高一数学人教B版(2019)必修3 |

|
|
| 格式 | pptx | ||
| 文件大小 | 868.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
8.2.4 三角恒等变换的应用
人教B版(2019)必修第三册
1.能用倍角公式导出半角公式.
2.掌握和差化积、积化和差公式的结构特征.
3.能利用三角恒等变换对三角函数式化简、求值和证明.
S2α :sin 2α = 2sin α·cos α;
C2α:cos 2α = cos2α sin2α = 1 2sin2α = 2cos2α 1;
T2α:tan 2α = .
忆一忆:写出α的倍角公式.
问题1:试以 cos α 表示 sin2,cos2,tan2 .
α 是 的二倍角,在倍角公式 cos 2α = 1 2sin2α 中,
以 α 代替 2α,以 代替 α 得:cos α = 1 2sin2 ,所以 sin2 = ①;
同理:根据倍角公式 cos 2α = 2cos2α 1得:cos2 = ②;
将①②两个等式的左右两边分别相除得:tan2 = .
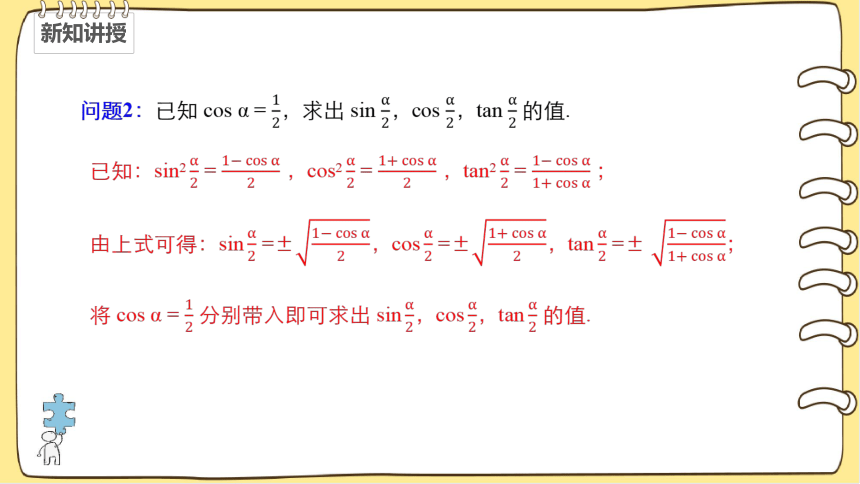
已知:sin2 = ,cos2 = ,tan2 = ;
问题2:已知 cos α = ,求出 sin ,cos ,tan 的值.
由上式可得:sin =±,cos =±,tan =± ;
将 cos α = 分别带入即可求出 sin ,cos ,tan 的值.
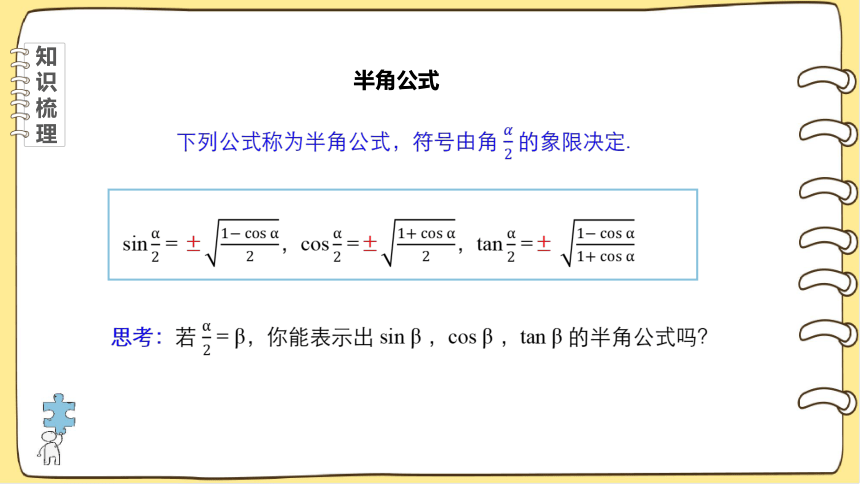
半角公式
下列公式称为半角公式,符号由角 的象限决定.
sin = ±,cos =±,tan =±
思考:若 = β,你能表示出 sin β ,cos β ,tan β 的半角公式吗?
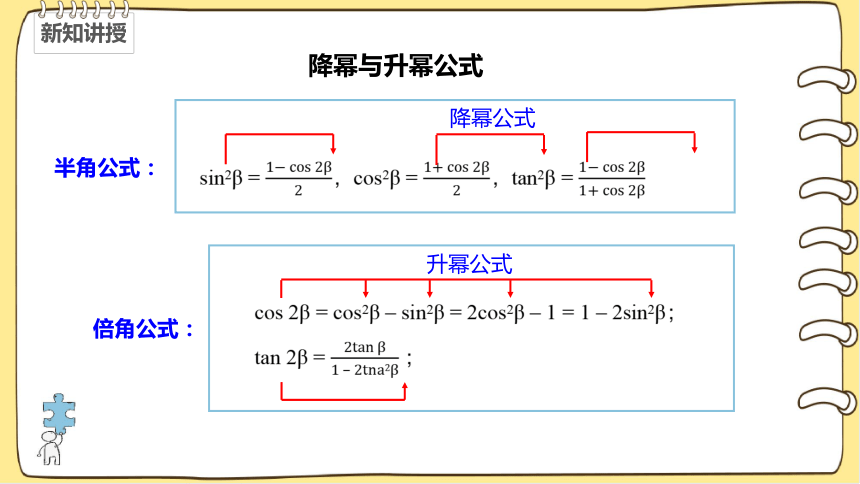
降幂与升幂公式
sin2β = ,cos2β = ,tan2β =
降幂公式
半角公式:
cos 2β = cos2β – sin2β = 2cos2β – 1 = 1 – 2sin2β;
tan 2β = ;
升幂公式
倍角公式:
1.公式的“本质”是用 角的余弦表示 角的正弦、余弦、正切.
2.根号前均有“± ”,它是由角“ ”所在象限来确定的,如果没有给定角的范围,“± ”应保留.
3.半角之间的相对性.
注意:
例1 求证:
证:左边
=右边.
例2 等腰三角形顶角的余弦值为,求它的底角的正弦、余弦和正切.
解:设顶角为α,底角为θ,则cos α=,α+2θ=2π,
∴θ∈(0,),cos 2θ=cos(π-α)=-cos α=-,
∴sin θ==,cos θ==,tanθ==.
问题3:求证:
(1)sin α·cos β = [sin (α+β) + sin (α – β)];
(2)sin θ + sin φ = 2 sin · cos .
证明:(1)因为 sin (α + β) = sin α·cos β + cos α·sin β,
sin (α – β) = sin α·cos β – cos α·sin β,
将以上两式的左右两边分别相加,得 sin (α + β) + sin (α – β) = 2sin α·cos β ①,
即 sin α·cos β = [sin (α+β) + sin (α – β)],故(1)得证;
求证:(2)sin θ + sin φ = 2 sin · cos .
证明:(2)由(1)可得:sin (α + β) + sin (α – β) = 2sin α·cos β ① ,
设:α = ,β = ,把 α、β 带入 ① 中,
即得:sin θ + sin φ = 2 sin · cos ,故(2)得证;
问题4:参照问题3,证明下列式子.
(1)cos α·cos β = [cos(α+β)+cos(α–β)];
(2)cos θ+cos φ = 2coscos .
思考:结合上述证明,你还能发现其他类似的式子吗?
积化和差与和差化积公式
(1)sin α·cos β = [sin(α + β) + sin(α – β)];
(2)cos α·sin β = [sin(α + β) – sin(α – β)];
(3)cos α·cos β = [cos(α + β) + cos(α – β)];
(4)sin α·sin β = – [cos(α + β) – cos(α – β)].
积化和差
(1)sin θ + sin φ = 2sin cos;
(2)sin θ – sin φ = 2cos sin;
(3)cos θ + cos φ = 2cos cos;
(4)cos θ – cos φ = –2sin sin.
和差化积
例3 已知sin(θ+)sin(θ-)=,求tan θ.
解:∵sin(θ+)sin(θ-)=-,
∴cos 2θ=-=,
∴tan θ=±2.
分析:先化简条件,再求值.
例4 求函数y=sin x[sin x-sin(x+)]的最值.
解:y=sin x[sin x-sin(x+)]=sin x·2cos(x+)sin(-)
=-sin xcos(x+)
=-[sin(2x+)+sin(-)]
=-sin(2x+)+,
∵sin(2x+)∈[-1,1],
∴当sin(2x+)=-1,即x=kπ-,k∈Z时,ymax=.
当sin(2x+)=1,即x=kπ+,k∈Z时,ymin=.
B
B
D
4.sin 15°sin 30°sin 75°的值是 .
根据今天所学,回答下列问题:
(1)说说你对倍角公式和半角公式间相互转化关系的理解;
(2)写出积化和差与和差化积公式公式.
8.2.4 三角恒等变换的应用
人教B版(2019)必修第三册
1.能用倍角公式导出半角公式.
2.掌握和差化积、积化和差公式的结构特征.
3.能利用三角恒等变换对三角函数式化简、求值和证明.
S2α :sin 2α = 2sin α·cos α;
C2α:cos 2α = cos2α sin2α = 1 2sin2α = 2cos2α 1;
T2α:tan 2α = .
忆一忆:写出α的倍角公式.
问题1:试以 cos α 表示 sin2,cos2,tan2 .
α 是 的二倍角,在倍角公式 cos 2α = 1 2sin2α 中,
以 α 代替 2α,以 代替 α 得:cos α = 1 2sin2 ,所以 sin2 = ①;
同理:根据倍角公式 cos 2α = 2cos2α 1得:cos2 = ②;
将①②两个等式的左右两边分别相除得:tan2 = .
已知:sin2 = ,cos2 = ,tan2 = ;
问题2:已知 cos α = ,求出 sin ,cos ,tan 的值.
由上式可得:sin =±,cos =±,tan =± ;
将 cos α = 分别带入即可求出 sin ,cos ,tan 的值.
半角公式
下列公式称为半角公式,符号由角 的象限决定.
sin = ±,cos =±,tan =±
思考:若 = β,你能表示出 sin β ,cos β ,tan β 的半角公式吗?
降幂与升幂公式
sin2β = ,cos2β = ,tan2β =
降幂公式
半角公式:
cos 2β = cos2β – sin2β = 2cos2β – 1 = 1 – 2sin2β;
tan 2β = ;
升幂公式
倍角公式:
1.公式的“本质”是用 角的余弦表示 角的正弦、余弦、正切.
2.根号前均有“± ”,它是由角“ ”所在象限来确定的,如果没有给定角的范围,“± ”应保留.
3.半角之间的相对性.
注意:
例1 求证:
证:左边
=右边.
例2 等腰三角形顶角的余弦值为,求它的底角的正弦、余弦和正切.
解:设顶角为α,底角为θ,则cos α=,α+2θ=2π,
∴θ∈(0,),cos 2θ=cos(π-α)=-cos α=-,
∴sin θ==,cos θ==,tanθ==.
问题3:求证:
(1)sin α·cos β = [sin (α+β) + sin (α – β)];
(2)sin θ + sin φ = 2 sin · cos .
证明:(1)因为 sin (α + β) = sin α·cos β + cos α·sin β,
sin (α – β) = sin α·cos β – cos α·sin β,
将以上两式的左右两边分别相加,得 sin (α + β) + sin (α – β) = 2sin α·cos β ①,
即 sin α·cos β = [sin (α+β) + sin (α – β)],故(1)得证;
求证:(2)sin θ + sin φ = 2 sin · cos .
证明:(2)由(1)可得:sin (α + β) + sin (α – β) = 2sin α·cos β ① ,
设:α = ,β = ,把 α、β 带入 ① 中,
即得:sin θ + sin φ = 2 sin · cos ,故(2)得证;
问题4:参照问题3,证明下列式子.
(1)cos α·cos β = [cos(α+β)+cos(α–β)];
(2)cos θ+cos φ = 2coscos .
思考:结合上述证明,你还能发现其他类似的式子吗?
积化和差与和差化积公式
(1)sin α·cos β = [sin(α + β) + sin(α – β)];
(2)cos α·sin β = [sin(α + β) – sin(α – β)];
(3)cos α·cos β = [cos(α + β) + cos(α – β)];
(4)sin α·sin β = – [cos(α + β) – cos(α – β)].
积化和差
(1)sin θ + sin φ = 2sin cos;
(2)sin θ – sin φ = 2cos sin;
(3)cos θ + cos φ = 2cos cos;
(4)cos θ – cos φ = –2sin sin.
和差化积
例3 已知sin(θ+)sin(θ-)=,求tan θ.
解:∵sin(θ+)sin(θ-)=-,
∴cos 2θ=-=,
∴tan θ=±2.
分析:先化简条件,再求值.
例4 求函数y=sin x[sin x-sin(x+)]的最值.
解:y=sin x[sin x-sin(x+)]=sin x·2cos(x+)sin(-)
=-sin xcos(x+)
=-[sin(2x+)+sin(-)]
=-sin(2x+)+,
∵sin(2x+)∈[-1,1],
∴当sin(2x+)=-1,即x=kπ-,k∈Z时,ymax=.
当sin(2x+)=1,即x=kπ+,k∈Z时,ymin=.
B
B
D
4.sin 15°sin 30°sin 75°的值是 .
根据今天所学,回答下列问题:
(1)说说你对倍角公式和半角公式间相互转化关系的理解;
(2)写出积化和差与和差化积公式公式.
