9.1.1 正弦定理 课件(26张PPT) 2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 9.1.1 正弦定理 课件(26张PPT) 2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
9.1.1 正弦定理
1.了解正弦定理的推导过程.
2.掌握正弦定理,并能解决一些简单的三角形度量问题.(重点、难点)
如图所示,若想知道河对岸的一点A与岸边一点B之间的距离,而且已经测量出了BC的长,也想办法得到了与的大小,你能借助这三个量,求出AB的长吗?
探究1:正弦定理
A
B
C
b
D
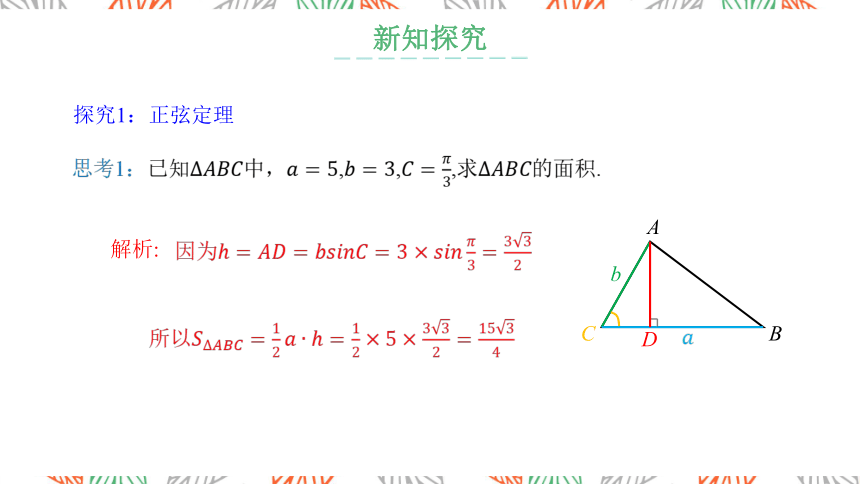
思考1:已知中,,,,求的面积.
因为
所以
解析:
解析:
A
B
C
b
D
思考2:一般地,在中,已知,与角,如何求的面积?
(1)若角为直角,,
所以
(2)若角为锐角,
所以
追问:角为钝角时,如何求的面积?
A
B
C
a
b
D
(2)若角为钝角,
所以
解析:
三角形面积公式
思考3:若已知与角或与的值,则的面积是多少?你有什么发现?
S ABC=absinC=acsinB=bbsinA
文字语言
符号语言
S ABC=absinC=acsinB=bbsinA
===
∵sin A>0,sin B>0,sin C>0,则有
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即:
例1
解析:
①
②
③
因为
所以由正弦定理
已知 ABC中,B=75°,C=60°,a =10,求A和b,c
已知两角及一边解三角形的一般步骤
(1)若所给边是已知角的对边时 ,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
①
②
③
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
①
②
③
AAS有且只有一解
方法总结
跟踪训练1
解:
由正弦定理得
同理
已知 ABC中,A=30°,C=45°,a =20,求B和b,c
例2
解析:
B
A
C
由正弦定理得:
①
因为所以或
在 ABC中,已知,a =2,b=2,A=30°求解这个三角形.
(1)当 时,
(2)当时,
此时是等腰三角形,从而由等角对等边可知 c = = 2.
此时为直角三角形,且为斜边,
则= = = 4;
解析:
B
A
C
①
检验1
内角和定理
检验2
大边对大角
由正弦定理 ,
①时,
②时,,舍去
,,
例3
在 ABC中,已知B=120°,c =6,b=3,求A,C及三角形面积
例4
解析:
由正弦定理
不存在这样的三角形
在 ABC中,已知A=30°,a =1,c=4,解这个三角形
已知两边及一边的对角解三角形的一般步骤
(1)可由正弦定理求另一边的对角,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)SSA解的个数可能:一解;两解;无解.根据正弦值范围、大边对大角、内角和定理判断.
方法总结
解析:
探究:如图,已知两边a、b 和其中边 a 的对角 A,利用几何图形,判断何时无解,一解,两解?
A
B
C
a
b
c
A
a
a
C
B
B
b
a
A 为 锐 角 图形
关系
解的个数 0 1 2 1
A 为 钝 角 或 直 角 图形
关系
解的个数 0 0 1 1
跟踪训练2
解:(1)由正弦定理得= ,∴===.
又=,=,∵,∴,故=30°,
∴.
由正弦定理得=,
∴===2.
∴,,.
在 ABC中,根据下列条件解这个三角形
(1)A=60°,c=,a=;
(2)a=,b=,B=45°.
解:(2)由正弦定理,得===.
∵∴或.
当时,,∴===;
当时,,∴===.
∴,,=或,,=.
跟踪训练2
在 ABC中,根据下列条件解这个三角形
(1)A=60°,c=,a=;
(2)a=,b=,B=45°.
探究点2:正弦定理的变形及应用
思考:观察 的形式,说说那么这个比值有什么特殊含义?
其中 c 是 △ABC 与 Rt△ABC 的外接圆的直径.
c
O
A
B
C
a
b
B'
(R为△ABC外接圆的半径).
所以对任意△ABC,均有
无论怎么移动 B',都有
所以在△ABC'中
作出如图所示图像,由图可知:
正弦定理的变形
(1) ,,;
(2),, ;
(3) ,,
知识归纳
在△ABC中,已知 sin2A + sin2B = sin2C,求证:△ABC是直角三角形.
设 = k,则 k ≠ 0,
且 sin A = ,sin B = ,sin C = ;
例5
解析:
又因为 sin2A + sin2B = sin2C,
所以 + = ,即 2 + b2 = c2;
因此由勾股定理的逆定理可知 ABC 是直角三角形.
在 △ABC 中,已知 ∠BAC 的角平分线 AD 与边 BC 相交于点 D,求证: .
证明:如图,设∠ADB = α,∠BAD = β,
则由题意可知∠ADC = π – α,∠CAD = β.
D
A
B
C
β
β
α
π–α
例6
在 ABD 和 ADC 中,应用正弦定理,
可得 , = ,
两式相除得 .
解:由 及正弦定理得
∴sin2A=sin2B,∴2A=2B或2A+2B=π,
即A=B或
故△ABC为等腰三角形或直角三角形.
在△ABC中,若 ,试判断△ABC的形状.
跟踪训练3
正弦定理
定理应用
已知两角和一边,解三角形
已知两边和其中一边的对角→解三角形
(注意多解问题)
思想方法
特殊到一般、方程思想
数形结合、分类讨论
本
课
知
识
文字语言:在一个三角形中,各边和它所对角的的正弦的比相等
9.1.1 正弦定理
1.了解正弦定理的推导过程.
2.掌握正弦定理,并能解决一些简单的三角形度量问题.(重点、难点)
如图所示,若想知道河对岸的一点A与岸边一点B之间的距离,而且已经测量出了BC的长,也想办法得到了与的大小,你能借助这三个量,求出AB的长吗?
探究1:正弦定理
A
B
C
b
D
思考1:已知中,,,,求的面积.
因为
所以
解析:
解析:
A
B
C
b
D
思考2:一般地,在中,已知,与角,如何求的面积?
(1)若角为直角,,
所以
(2)若角为锐角,
所以
追问:角为钝角时,如何求的面积?
A
B
C
a
b
D
(2)若角为钝角,
所以
解析:
三角形面积公式
思考3:若已知与角或与的值,则的面积是多少?你有什么发现?
S ABC=absinC=acsinB=bbsinA
文字语言
符号语言
S ABC=absinC=acsinB=bbsinA
===
∵sin A>0,sin B>0,sin C>0,则有
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即:
例1
解析:
①
②
③
因为
所以由正弦定理
已知 ABC中,B=75°,C=60°,a =10,求A和b,c
已知两角及一边解三角形的一般步骤
(1)若所给边是已知角的对边时 ,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
①
②
③
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
①
②
③
AAS有且只有一解
方法总结
跟踪训练1
解:
由正弦定理得
同理
已知 ABC中,A=30°,C=45°,a =20,求B和b,c
例2
解析:
B
A
C
由正弦定理得:
①
因为所以或
在 ABC中,已知,a =2,b=2,A=30°求解这个三角形.
(1)当 时,
(2)当时,
此时是等腰三角形,从而由等角对等边可知 c = = 2.
此时为直角三角形,且为斜边,
则= = = 4;
解析:
B
A
C
①
检验1
内角和定理
检验2
大边对大角
由正弦定理 ,
①时,
②时,,舍去
,,
例3
在 ABC中,已知B=120°,c =6,b=3,求A,C及三角形面积
例4
解析:
由正弦定理
不存在这样的三角形
在 ABC中,已知A=30°,a =1,c=4,解这个三角形
已知两边及一边的对角解三角形的一般步骤
(1)可由正弦定理求另一边的对角,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)SSA解的个数可能:一解;两解;无解.根据正弦值范围、大边对大角、内角和定理判断.
方法总结
解析:
探究:如图,已知两边a、b 和其中边 a 的对角 A,利用几何图形,判断何时无解,一解,两解?
A
B
C
a
b
c
A
a
a
C
B
B
b
a
A 为 锐 角 图形
关系
解的个数 0 1 2 1
A 为 钝 角 或 直 角 图形
关系
解的个数 0 0 1 1
跟踪训练2
解:(1)由正弦定理得= ,∴===.
又=,=,∵,∴,故=30°,
∴.
由正弦定理得=,
∴===2.
∴,,.
在 ABC中,根据下列条件解这个三角形
(1)A=60°,c=,a=;
(2)a=,b=,B=45°.
解:(2)由正弦定理,得===.
∵∴或.
当时,,∴===;
当时,,∴===.
∴,,=或,,=.
跟踪训练2
在 ABC中,根据下列条件解这个三角形
(1)A=60°,c=,a=;
(2)a=,b=,B=45°.
探究点2:正弦定理的变形及应用
思考:观察 的形式,说说那么这个比值有什么特殊含义?
其中 c 是 △ABC 与 Rt△ABC 的外接圆的直径.
c
O
A
B
C
a
b
B'
(R为△ABC外接圆的半径).
所以对任意△ABC,均有
无论怎么移动 B',都有
所以在△ABC'中
作出如图所示图像,由图可知:
正弦定理的变形
(1) ,,;
(2),, ;
(3) ,,
知识归纳
在△ABC中,已知 sin2A + sin2B = sin2C,求证:△ABC是直角三角形.
设 = k,则 k ≠ 0,
且 sin A = ,sin B = ,sin C = ;
例5
解析:
又因为 sin2A + sin2B = sin2C,
所以 + = ,即 2 + b2 = c2;
因此由勾股定理的逆定理可知 ABC 是直角三角形.
在 △ABC 中,已知 ∠BAC 的角平分线 AD 与边 BC 相交于点 D,求证: .
证明:如图,设∠ADB = α,∠BAD = β,
则由题意可知∠ADC = π – α,∠CAD = β.
D
A
B
C
β
β
α
π–α
例6
在 ABD 和 ADC 中,应用正弦定理,
可得 , = ,
两式相除得 .
解:由 及正弦定理得
∴sin2A=sin2B,∴2A=2B或2A+2B=π,
即A=B或
故△ABC为等腰三角形或直角三角形.
在△ABC中,若 ,试判断△ABC的形状.
跟踪训练3
正弦定理
定理应用
已知两角和一边,解三角形
已知两边和其中一边的对角→解三角形
(注意多解问题)
思想方法
特殊到一般、方程思想
数形结合、分类讨论
本
课
知
识
文字语言:在一个三角形中,各边和它所对角的的正弦的比相等
