10.3 复数的三角形式及其运算 课件(共21张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 10.3 复数的三角形式及其运算 课件(共21张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 642.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
*10.3 复数的三角形式及其运算
第十章 复数
1. 了解复数的三角形式及辐角与辐角主值的概念;
2. 能进行复数三角形式与代数形式的互化;
3. 了解复数乘除运算的三角形式及其几何意义.
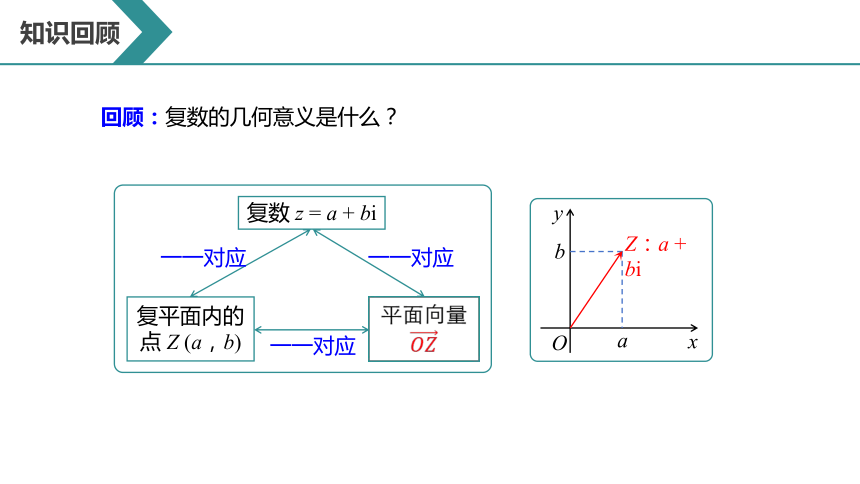
复数 z = a + bi
一一对应
一一对应
复平面内的点 Z (a,b)
平面向量
一一对应
a
b
Z:a + bi
O
y
x
回顾:复数的几何意义是什么?
知识点 1:复数的三角形式
如图,若非零复数 z = a + bi (a,b∈R) 在复平面内对应点 Z (a,b),
且 r 为向量 OZ 的模,θ 是以 x 轴正半轴为始边、射线 OZ 为终边的一个角,
则 r = |z| = .
根据余弦、正弦的定义可知 cos θ = ,sin θ = ,
因此 a = rcos θ,b = rsin θ,
从而 z = a + bi = (rcos θ) + (rsin θ)i = r(cos θ + isin θ).
a
b
Z
O
y
x
r
θ
rsin θ
rcos θ
思考:当点在实轴或虚轴上时,这个结论成立吗?
z = a + bi = r (cos θ + isin θ)
r = |z| =
cos θ =
sin θ =
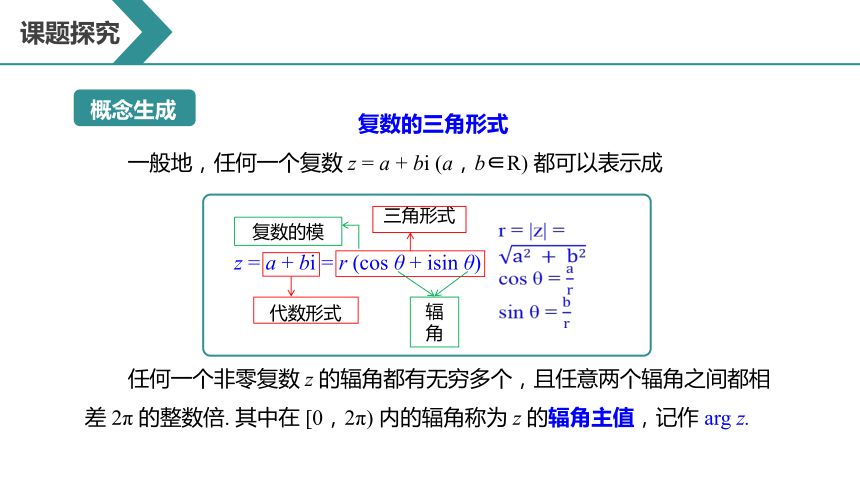
复数的三角形式
一般地,任何一个复数 z = a + bi (a,b∈R) 都可以表示成
任何一个非零复数 z 的辐角都有无穷多个,且任意两个辐角之间都相差 2π 的整数倍. 其中在 [0,2π) 内的辐角称为 z 的辐角主值,记作 arg z.
代数形式
三角形式
辐角
复数的模
概念生成
例1 把下列复数的代数形式改写成三角形式.
(1) + i ; (2)i.
例1 把下列复数的代数形式改写成三角形式.
(1) + i ; (2)i.
变式:分别指出下列复数的模和辐角主值,并把这些复数表示成代数形式.
(1)4(cos +isin ) ; (2)2(cos -isin ).
归纳总结
复数的代数形式化为三角形式的四个步骤:
(1)先求复数的模.
(2)确定辐角所在的象限.
(3)根据象限求出辐角.
(4)求出复数的三角形式.
知识点 2:复数三角形式的乘除法
问题 1:z1 = r1(cos θ1 + isin θ1),z2 = r2(cos θ2 + isin θ2),试求出 z1z2.
即
问题 2:如何用文字语言来表述复数乘法的三角表示公式?
模相乘,辐角相加:两个复数相乘,积的模等于各复数的模的积,积的辐角等于各复数的辐角的和.
复数乘法的几何意义
把向量 绕点 O 按逆时针方向旋转角 θ2,
两个复数 z1,z2 相乘时,
再把它的模变为原来的 r2 倍,得到向量
表示的复数就是积 z1z2.
(如果 θ2 < 0,就要把 绕点 O 按顺时针方向旋转角 |θ2|)
作出与复数 z1,z2 对应的向量
概念生成
问题 3:如何解释 i2 = – 1 和 (– 1)2 = 1 的几何意义?
所以 i2 = –1可以改写为
几何意义:将 i 对应的向量绕点 O 按逆时针旋转 得到 –1 对应的向量;
(–1)2 = 1可以改写为
因为 ,
几何意义:将 –1 对应的向量绕点 O 按逆时针旋转 π,得到 1 对应的向量.
[r(cos θ + isin θ)]n = rn[cos (nθ) + isin (nθ)]
两个复数三角形式的乘法及其几何意义,可推广到有限个复数的三角形式相乘.
特别地,如果 n∈N,则
归纳总结
问题 4:复数除法运算是乘法运算的逆运算.根据复数乘法运算的三角表示,如何推导出复数除法运算的三角表示?
所以根据复数除法的定义,有
因为
设
,且 z1 ≠ z2.
= [cos (θ1 – θ2) + isin (θ1 – θ2)]
模数相除,辐角相减:
两个复数相除,商的模等于被除数模除以除数的模所得的商,商的辐角等于被除数的辐角减去除数的辐角所得的差.
= [cos (θ1 – θ2) + isin (θ1 – θ2)]
归纳总结
复数除法的几何意义
把向量 绕点 O 按顺时针方向旋转角 θ2 (θ2 > 0),
两个复数 z1,z2 相除时,
再把它的模变为原来的 倍,得到向量
表示的复数就是商 .
作出与复数 z1,z2 对应的向量
概念生成
例2 计算.
(1)5(cos +isin )×2(cos +isin ); (2).
解:(1)原式=10(cos +isin )=10()=;
(2)原式===16(cos +isin )=16i.
A
C
*10.3 复数的三角形式及其运算
第十章 复数
1. 了解复数的三角形式及辐角与辐角主值的概念;
2. 能进行复数三角形式与代数形式的互化;
3. 了解复数乘除运算的三角形式及其几何意义.
复数 z = a + bi
一一对应
一一对应
复平面内的点 Z (a,b)
平面向量
一一对应
a
b
Z:a + bi
O
y
x
回顾:复数的几何意义是什么?
知识点 1:复数的三角形式
如图,若非零复数 z = a + bi (a,b∈R) 在复平面内对应点 Z (a,b),
且 r 为向量 OZ 的模,θ 是以 x 轴正半轴为始边、射线 OZ 为终边的一个角,
则 r = |z| = .
根据余弦、正弦的定义可知 cos θ = ,sin θ = ,
因此 a = rcos θ,b = rsin θ,
从而 z = a + bi = (rcos θ) + (rsin θ)i = r(cos θ + isin θ).
a
b
Z
O
y
x
r
θ
rsin θ
rcos θ
思考:当点在实轴或虚轴上时,这个结论成立吗?
z = a + bi = r (cos θ + isin θ)
r = |z| =
cos θ =
sin θ =
复数的三角形式
一般地,任何一个复数 z = a + bi (a,b∈R) 都可以表示成
任何一个非零复数 z 的辐角都有无穷多个,且任意两个辐角之间都相差 2π 的整数倍. 其中在 [0,2π) 内的辐角称为 z 的辐角主值,记作 arg z.
代数形式
三角形式
辐角
复数的模
概念生成
例1 把下列复数的代数形式改写成三角形式.
(1) + i ; (2)i.
例1 把下列复数的代数形式改写成三角形式.
(1) + i ; (2)i.
变式:分别指出下列复数的模和辐角主值,并把这些复数表示成代数形式.
(1)4(cos +isin ) ; (2)2(cos -isin ).
归纳总结
复数的代数形式化为三角形式的四个步骤:
(1)先求复数的模.
(2)确定辐角所在的象限.
(3)根据象限求出辐角.
(4)求出复数的三角形式.
知识点 2:复数三角形式的乘除法
问题 1:z1 = r1(cos θ1 + isin θ1),z2 = r2(cos θ2 + isin θ2),试求出 z1z2.
即
问题 2:如何用文字语言来表述复数乘法的三角表示公式?
模相乘,辐角相加:两个复数相乘,积的模等于各复数的模的积,积的辐角等于各复数的辐角的和.
复数乘法的几何意义
把向量 绕点 O 按逆时针方向旋转角 θ2,
两个复数 z1,z2 相乘时,
再把它的模变为原来的 r2 倍,得到向量
表示的复数就是积 z1z2.
(如果 θ2 < 0,就要把 绕点 O 按顺时针方向旋转角 |θ2|)
作出与复数 z1,z2 对应的向量
概念生成
问题 3:如何解释 i2 = – 1 和 (– 1)2 = 1 的几何意义?
所以 i2 = –1可以改写为
几何意义:将 i 对应的向量绕点 O 按逆时针旋转 得到 –1 对应的向量;
(–1)2 = 1可以改写为
因为 ,
几何意义:将 –1 对应的向量绕点 O 按逆时针旋转 π,得到 1 对应的向量.
[r(cos θ + isin θ)]n = rn[cos (nθ) + isin (nθ)]
两个复数三角形式的乘法及其几何意义,可推广到有限个复数的三角形式相乘.
特别地,如果 n∈N,则
归纳总结
问题 4:复数除法运算是乘法运算的逆运算.根据复数乘法运算的三角表示,如何推导出复数除法运算的三角表示?
所以根据复数除法的定义,有
因为
设
,且 z1 ≠ z2.
= [cos (θ1 – θ2) + isin (θ1 – θ2)]
模数相除,辐角相减:
两个复数相除,商的模等于被除数模除以除数的模所得的商,商的辐角等于被除数的辐角减去除数的辐角所得的差.
= [cos (θ1 – θ2) + isin (θ1 – θ2)]
归纳总结
复数除法的几何意义
把向量 绕点 O 按顺时针方向旋转角 θ2 (θ2 > 0),
两个复数 z1,z2 相除时,
再把它的模变为原来的 倍,得到向量
表示的复数就是商 .
作出与复数 z1,z2 对应的向量
概念生成
例2 计算.
(1)5(cos +isin )×2(cos +isin ); (2).
解:(1)原式=10(cos +isin )=10()=;
(2)原式===16(cos +isin )=16i.
A
C
