11.1.1 空间几何体与斜二测画法 课件(共20张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.1 空间几何体与斜二测画法 课件(共20张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 15:30:43 | ||
图片预览





文档简介
(共20张PPT)
11.1.1 空间几何体与斜二测画法
1.认识空间几何体.
2.会用斜二测画法画水平放置的平面图形的直观图.(重点)
3.会用斜二测画法画常见的柱、锥、台的直观图.
如图是国家游泳中心(又称“水立方”),它可以抽象成一个几何体—长方体,你能试着画出一个长方体吗?上下底面的长方形,怎么画更有立体感?
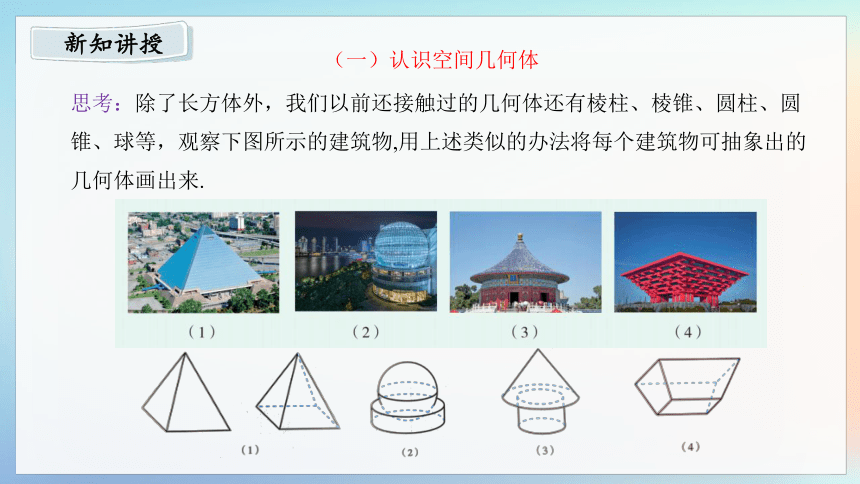
(一)认识空间几何体
思考:除了长方体外,我们以前还接触过的几何体还有棱柱、棱锥、圆柱、圆锥、球等,观察下图所示的建筑物,用上述类似的办法将每个建筑物可抽象出的几何体画出来.
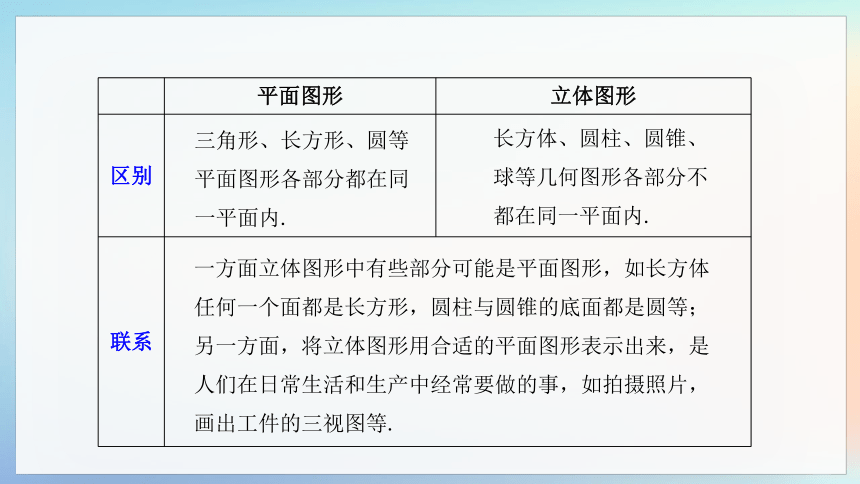
平面图形 立体图形
区别
联系 三角形、长方形、圆等平面图形各部分都在同一平面内.
长方体、圆柱、圆锥、球等几何图形各部分不都在同一平面内.
一方面立体图形中有些部分可能是平面图形,如长方体任何一个面都是长方形,圆柱与圆锥的底面都是圆等;另一方面,将立体图形用合适的平面图形表示出来,是人们在日常生活和生产中经常要做的事,如拍摄照片,画出工件的三视图等.
下图(1)(2)是从不同角度拍摄同一个魔方的照片,哪个图更能给人立体感?
图(1)更能给人立体感.
立体几何中用来表示空间图形的平面图形习惯上称为空间图形的直观图,为了使直观图具有立体感,人们常使用斜二测画法来作直观图.
思考
(2)斜二测画法
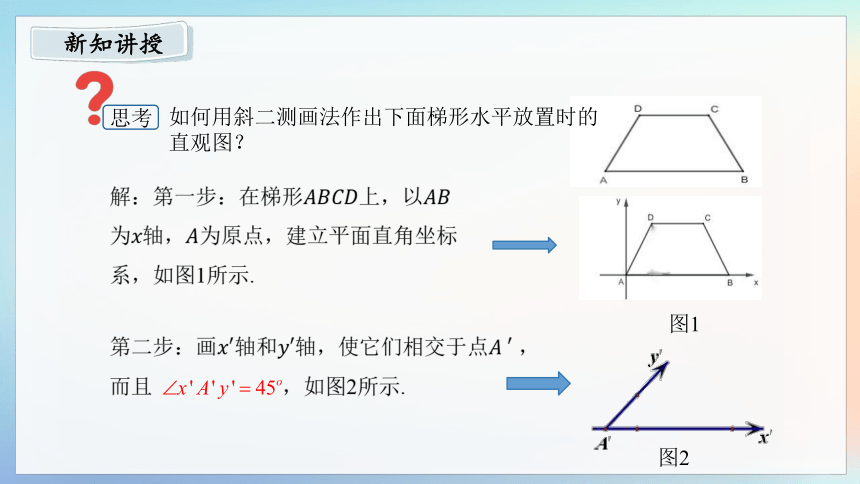
如何用斜二测画法作出下面梯形水平放置时的直观图?
解:第一步:在梯形上,以为轴,为原点,建立平面直角坐标系,如图1所示.
第二步:画轴和轴,使它们相交于点 ,而且 ,如图2所示.
图1
图2
思考
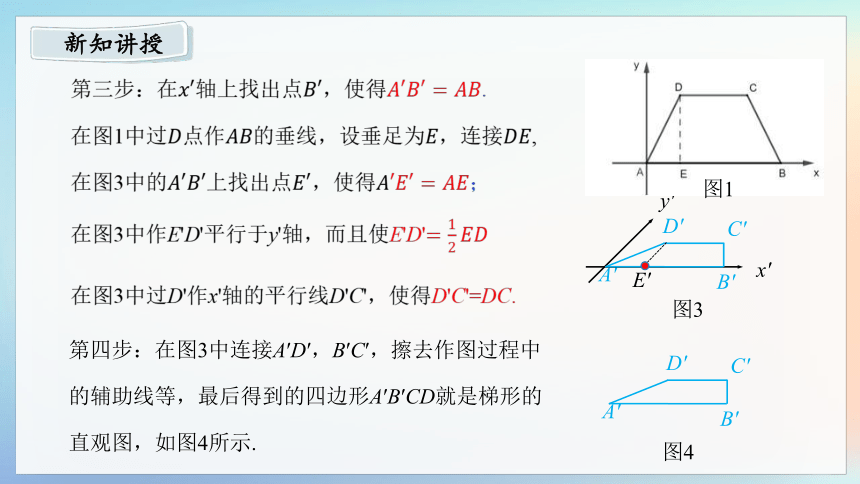
第三步:在轴上找出点,使得.
在图1中过点作的垂线,设垂足为,连接,
在图3中的上找出点,使得;
在图3中作E'D'平行于y'轴,而且使E'D'
在图3中过D'作x'轴的平行线D'C',使得D'C'=DC.
第四步:在图3中连接A′D′,B′C′,擦去作图过程中的辅助线等,最后得到的四边形A′B′CD就是梯形的直观图,如图4所示.
A′
x′
y′
B′
C′
D′
E′
图3
A′
B′
C′
D′
图4
图1
用斜二测画法作水平放置的平面图形直观图的步骤:
(1)在平面图形上取互相垂直的x轴和y轴,作出与之对应的 x′ 轴和 y′ 轴,使得它们正方向的夹角为 45°(或135°);
(2)平面图形中与x轴平行(或重合)的线段画成与 y′ 轴重合(或平行)的线段,且长度不变.平面图形中与y轴平行(或重合)的线段画成与 y′ 轴重合(或平行)的线段,且长度为原来长度的一半.
(3)连接有关线段,擦去作图过程中的辅助线.
知识归纳
1.用斜二测画法画水平放置的平面图形的直观图时,下列结论是否正确?正确的在括号内画“√”,错误的画“×”
(1)相等的线段在直观图中仍然相等. ( )
(2)平行的线段在直观图中仍然平行. ( )
(3)一个角的直观图仍是一个角. ( )
(4)相等的角在直观图中仍然相等. ( )
√
√
×
√
2.用斜二测画法画边长为4 cm的水平放置的正三角形的直观图.
解: (1)如图①所示,以BC边所在的直线为x轴,以BC边上的高线AO所在的直线为y轴,建立平面直角坐标系.
(2)画对应的x′轴、y′轴,使∠x′O′y′=45°.在x′轴上截取O′B′=O′C′=2 cm,在y′轴上截取O′A′=OA,连结A′B′,A′C′,则三角形A′B′C′即为正三角形ABC的直观图,如图②所示.
画一个水平放置的长为4,宽为3,高为2的长方体的直观图.
(1)首先,用上面的方法作出水平放置的长为4,宽为3的长方形的直观图(保留坐标轴,如右图所示)
(2)过A作z '轴,使之垂直于x '轴,在z '轴上截取AA ' =2,过B,C,D分别作z'的平行线BB',CC',DD',并使BB'=CC'=DD'=2,然后连接A'B',B'C',C'D',D'A',如图2所示:
思考
(3)擦去作图3过程中的辅助线,并把被面遮挡住的线段AD,DC,DD′改成虚线(或擦除),由此得到的就是所求长方体的直观图,如右图所示.
用斜二测画法作立体图形直观图的步骤:
(1)在立体图形中取水平平面,在其中取互相垂直的x轴与y轴,作出水平平面上图形的直观图(保留 x′ 轴 y′ 轴).
(2)在立体图形中,过x轴与y轴的交点取z轴,并使z轴垂直于x轴与y轴.过 x′ 轴与 y′ 轴的交点作z轴对应的z ' 轴,且 z ' 轴垂直于 x′ 轴与 y′ 轴 .图形中与z轴平行(或重合)的线段画成与 z ' 轴平行(或重合)的线段,且长度不变.连接有关线段.
(3)擦去辅助线,并把被面遮挡住的线段改成虚线(或擦除).
口诀:平行依旧垂改斜,横等纵半竖不变;
眼见为实遮为虚,空间观感好体现.
方法归纳
例1
如图所示, A′B′C′是水平放置的平面图形的斜二测直观图,将其还原成平面图形.
解:①画出直角坐标系xOy,在x轴的正方向上取OA=O′A′,即CA=C′A′;
②过B′作B′D′∥y′轴,交x′轴于点D′,在OA上取OD=O′D′,过D作DB∥y轴,且使DB=2D′B′; ③连接AB,BC,得△ABC.则△ABC即为△A′B′C′对应的平面图形,如图所示.
注意:平行依旧斜改垂;横等纵倍竖不变.
3.已知水平放置的 ABC按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么 ABC是一个( )
A.等边三角形 B.直角三角形C.等腰三角形 D.钝角三角形
解:根据斜二测画法还原△ABC在直角坐标系中的图形,如图,
所以△ABC是一个等边三角形.
A
则BC=B' C' =2,AO=2A' O' =,
AC=AB ==2,
例2
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为________.
2+
解析
小结
按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积的关系:S直观图=。
DC=AB=,
BC=AB+AD=+1,
S梯形ABCD=(AD+BC) DC
=(+)×=+,
S=S梯形ABCD=2+
4.如图,一个水平放置的平面图形的直观图是一个底角为45°的等腰梯形,已知直观图OA′B′C′的面积为4,则该平面图形的面积为 ( )
C
解析:由S原图形=2S直观图,得S原图形2×4=8.
按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积的关系:S直观图=
11.1.1 空间几何体与斜二测画法
1.认识空间几何体.
2.会用斜二测画法画水平放置的平面图形的直观图.(重点)
3.会用斜二测画法画常见的柱、锥、台的直观图.
如图是国家游泳中心(又称“水立方”),它可以抽象成一个几何体—长方体,你能试着画出一个长方体吗?上下底面的长方形,怎么画更有立体感?
(一)认识空间几何体
思考:除了长方体外,我们以前还接触过的几何体还有棱柱、棱锥、圆柱、圆锥、球等,观察下图所示的建筑物,用上述类似的办法将每个建筑物可抽象出的几何体画出来.
平面图形 立体图形
区别
联系 三角形、长方形、圆等平面图形各部分都在同一平面内.
长方体、圆柱、圆锥、球等几何图形各部分不都在同一平面内.
一方面立体图形中有些部分可能是平面图形,如长方体任何一个面都是长方形,圆柱与圆锥的底面都是圆等;另一方面,将立体图形用合适的平面图形表示出来,是人们在日常生活和生产中经常要做的事,如拍摄照片,画出工件的三视图等.
下图(1)(2)是从不同角度拍摄同一个魔方的照片,哪个图更能给人立体感?
图(1)更能给人立体感.
立体几何中用来表示空间图形的平面图形习惯上称为空间图形的直观图,为了使直观图具有立体感,人们常使用斜二测画法来作直观图.
思考
(2)斜二测画法
如何用斜二测画法作出下面梯形水平放置时的直观图?
解:第一步:在梯形上,以为轴,为原点,建立平面直角坐标系,如图1所示.
第二步:画轴和轴,使它们相交于点 ,而且 ,如图2所示.
图1
图2
思考
第三步:在轴上找出点,使得.
在图1中过点作的垂线,设垂足为,连接,
在图3中的上找出点,使得;
在图3中作E'D'平行于y'轴,而且使E'D'
在图3中过D'作x'轴的平行线D'C',使得D'C'=DC.
第四步:在图3中连接A′D′,B′C′,擦去作图过程中的辅助线等,最后得到的四边形A′B′CD就是梯形的直观图,如图4所示.
A′
x′
y′
B′
C′
D′
E′
图3
A′
B′
C′
D′
图4
图1
用斜二测画法作水平放置的平面图形直观图的步骤:
(1)在平面图形上取互相垂直的x轴和y轴,作出与之对应的 x′ 轴和 y′ 轴,使得它们正方向的夹角为 45°(或135°);
(2)平面图形中与x轴平行(或重合)的线段画成与 y′ 轴重合(或平行)的线段,且长度不变.平面图形中与y轴平行(或重合)的线段画成与 y′ 轴重合(或平行)的线段,且长度为原来长度的一半.
(3)连接有关线段,擦去作图过程中的辅助线.
知识归纳
1.用斜二测画法画水平放置的平面图形的直观图时,下列结论是否正确?正确的在括号内画“√”,错误的画“×”
(1)相等的线段在直观图中仍然相等. ( )
(2)平行的线段在直观图中仍然平行. ( )
(3)一个角的直观图仍是一个角. ( )
(4)相等的角在直观图中仍然相等. ( )
√
√
×
√
2.用斜二测画法画边长为4 cm的水平放置的正三角形的直观图.
解: (1)如图①所示,以BC边所在的直线为x轴,以BC边上的高线AO所在的直线为y轴,建立平面直角坐标系.
(2)画对应的x′轴、y′轴,使∠x′O′y′=45°.在x′轴上截取O′B′=O′C′=2 cm,在y′轴上截取O′A′=OA,连结A′B′,A′C′,则三角形A′B′C′即为正三角形ABC的直观图,如图②所示.
画一个水平放置的长为4,宽为3,高为2的长方体的直观图.
(1)首先,用上面的方法作出水平放置的长为4,宽为3的长方形的直观图(保留坐标轴,如右图所示)
(2)过A作z '轴,使之垂直于x '轴,在z '轴上截取AA ' =2,过B,C,D分别作z'的平行线BB',CC',DD',并使BB'=CC'=DD'=2,然后连接A'B',B'C',C'D',D'A',如图2所示:
思考
(3)擦去作图3过程中的辅助线,并把被面遮挡住的线段AD,DC,DD′改成虚线(或擦除),由此得到的就是所求长方体的直观图,如右图所示.
用斜二测画法作立体图形直观图的步骤:
(1)在立体图形中取水平平面,在其中取互相垂直的x轴与y轴,作出水平平面上图形的直观图(保留 x′ 轴 y′ 轴).
(2)在立体图形中,过x轴与y轴的交点取z轴,并使z轴垂直于x轴与y轴.过 x′ 轴与 y′ 轴的交点作z轴对应的z ' 轴,且 z ' 轴垂直于 x′ 轴与 y′ 轴 .图形中与z轴平行(或重合)的线段画成与 z ' 轴平行(或重合)的线段,且长度不变.连接有关线段.
(3)擦去辅助线,并把被面遮挡住的线段改成虚线(或擦除).
口诀:平行依旧垂改斜,横等纵半竖不变;
眼见为实遮为虚,空间观感好体现.
方法归纳
例1
如图所示, A′B′C′是水平放置的平面图形的斜二测直观图,将其还原成平面图形.
解:①画出直角坐标系xOy,在x轴的正方向上取OA=O′A′,即CA=C′A′;
②过B′作B′D′∥y′轴,交x′轴于点D′,在OA上取OD=O′D′,过D作DB∥y轴,且使DB=2D′B′; ③连接AB,BC,得△ABC.则△ABC即为△A′B′C′对应的平面图形,如图所示.
注意:平行依旧斜改垂;横等纵倍竖不变.
3.已知水平放置的 ABC按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么 ABC是一个( )
A.等边三角形 B.直角三角形C.等腰三角形 D.钝角三角形
解:根据斜二测画法还原△ABC在直角坐标系中的图形,如图,
所以△ABC是一个等边三角形.
A
则BC=B' C' =2,AO=2A' O' =,
AC=AB ==2,
例2
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为________.
2+
解析
小结
按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积的关系:S直观图=。
DC=AB=,
BC=AB+AD=+1,
S梯形ABCD=(AD+BC) DC
=(+)×=+,
S=S梯形ABCD=2+
4.如图,一个水平放置的平面图形的直观图是一个底角为45°的等腰梯形,已知直观图OA′B′C′的面积为4,则该平面图形的面积为 ( )
C
解析:由S原图形=2S直观图,得S原图形2×4=8.
按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积的关系:S直观图=
