11.1.4 棱锥与棱台 课件(20张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.4 棱锥与棱台 课件(20张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1007.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
11.1.4 棱锥与棱台
1.了解棱锥、棱台的定义和结构特征
2.知道棱锥、棱台的表面积计算公式,能用公式解决简单的实际问题.(重点)
下图所示的建筑是什么几何体呢?你还能举出一些例子吗?
情景导入
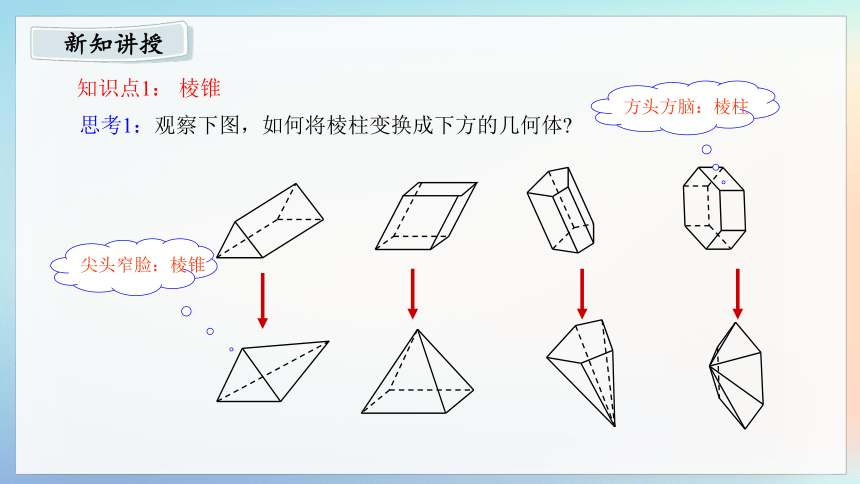
思考1:观察下图,如何将棱柱变换成下方的几何体
方头方脑:棱柱
尖头窄脸:棱锥
知识点1: 棱锥
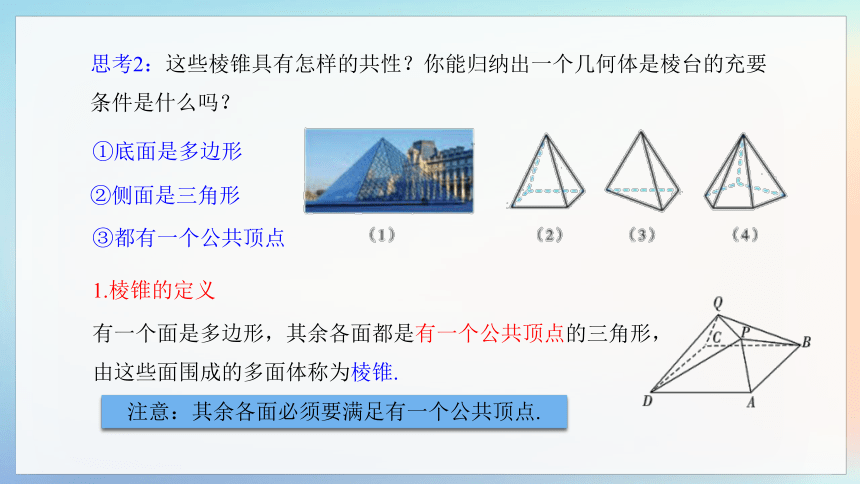
思考2:这些棱锥具有怎样的共性?你能归纳出一个几何体是棱台的充要条件是什么吗?
1.棱锥的定义
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体称为棱锥.
注意:其余各面必须要满足有一个公共顶点.
①底面是多边形
②侧面是三角形
③都有一个公共顶点
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
O
棱锥的高
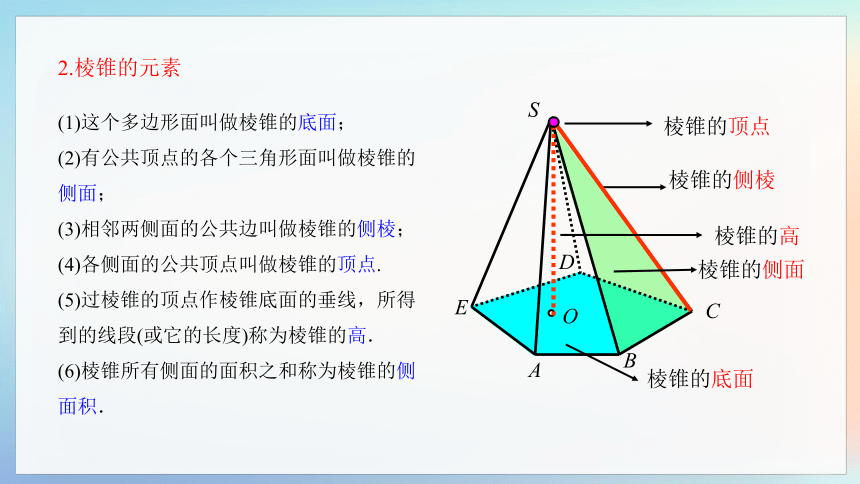
(1)这个多边形面叫做棱锥的底面;
(2)有公共顶点的各个三角形面叫做棱锥的侧面;
(3)相邻两侧面的公共边叫做棱锥的侧棱;
(4)各侧面的公共顶点叫做棱锥的顶点.
(5)过棱锥的顶点作棱锥底面的垂线,所得到的线段(或它的长度)称为棱锥的高.
(6)棱锥所有侧面的面积之和称为棱锥的侧面积.
2.棱锥的元素
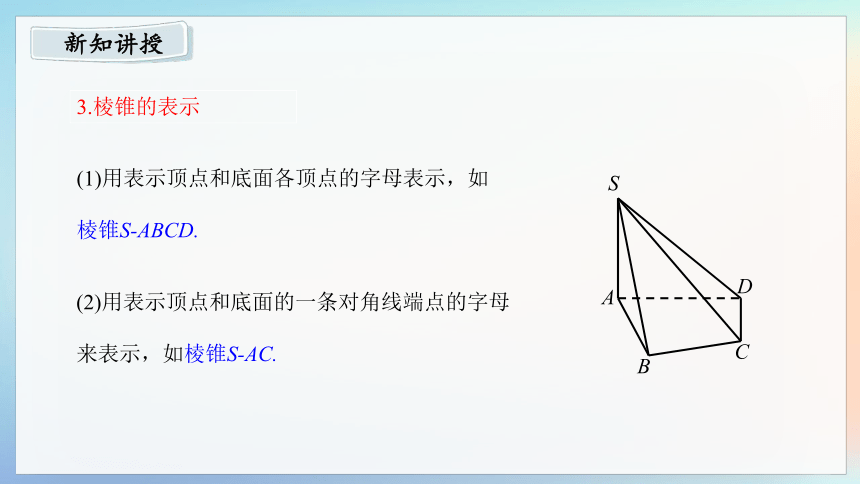
(1)用表示顶点和底面各顶点的字母表示,如棱锥S-ABCD.
(2)用表示顶点和底面的一条对角线端点的字母来表示,如棱锥S-AC.
S
A
B
C
D
3.棱锥的表示
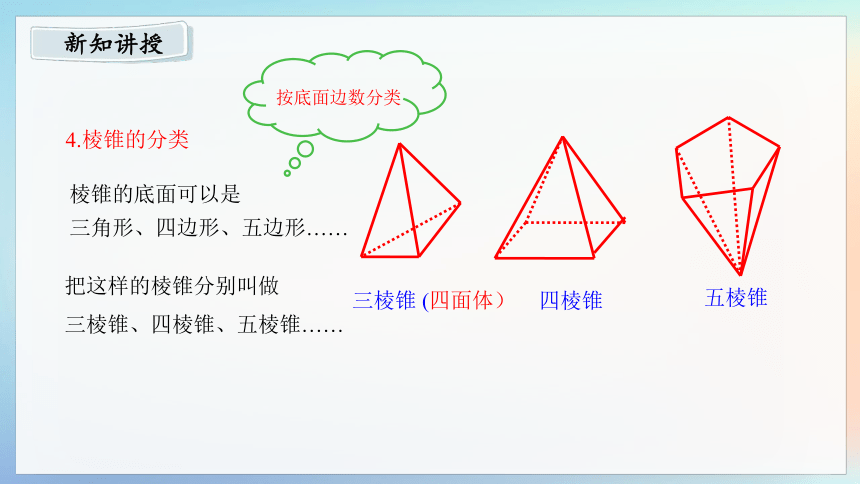
4.棱锥的分类
棱锥的底面可以是
三角形、四边形、五边形……
把这样的棱锥分别叫做
三棱锥、四棱锥、五棱锥……
三棱锥 (四面体)
四棱锥
五棱锥
按底面边数分类
正棱椎:
如图,PO为棱锥P-ABCD的高,因此PO⊥面ABCD.
从而可知:
如果棱锥的底面是正多边形,且棱锥的顶点与底面中心的连线垂直于底面,则称这个棱锥为正棱锥.正棱锥的侧面都全等,而且都是等腰三角形,这些等腰三角形底边上的高也都相等,称为棱锥的斜高.
1.能保证棱锥是正棱锥的一个条件是( )
(A)底面为正多边形 (B)各侧棱都相等
(C)各侧面与底面都是全等的正三角形 (D)各侧面都是等腰三角形
C
例1 如图是底面边长为1且侧棱长为 的正六棱锥
(1)写出直线PA与直线CD,直线PA与面ABCDEF之间的关系;
(2)求棱锥的高和斜高;
(3)求棱锥的侧面积.
解:(1)直线PA与直线CD异面,直线PA∩面ABCDEF=A.
(2)作出棱锥的高PO,因为是正六棱锥,所以O是底面的中心,连接OC,可知OC=1.
在Rt△POC中,可知:
设BC的中点为M,由△PBC为等腰三角形可知,PM⊥MC ,
因此PM为斜高,从而
(3)因为△PBC的面积为:
故棱锥的侧面积为:
2.已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为 ,计算它的高和斜高.
因为底面正方形ABCD的面积是16,所以BC=4,MB=OM=2,
又因为VB= ,在Rt VOB中,由勾股定理得
在Rt△VOM中,由勾股定理得
即正四棱锥的高为6,斜高为
解:
知识点2:棱台
思考1:观察下图,如何将棱锥变换成下方的几何体
棱锥被平行于底面的平面所截,截面和底面间的多面体叫做棱台.
1.棱台的定义:
(1)原棱锥的底面与截面分别称为棱台的下底面和上底面,其余各面称为棱台的侧面;
(2)相邻两侧面的公共边称为棱台的侧棱.
(3)过棱台一个底面上的任意一个顶点,
作另一个底面的垂线所得到的线段(或它的长度)称为棱台的高.
上底面
侧面
侧棱
高
下底面
2.棱台的元素
3.棱台的性质:两底面是相似的多边形,侧棱的延长线交于一点.
思考2:下图中的几何体是不是棱台 为什么
不是.
因为棱台是用一个平行于棱锥底面的平面去截棱锥得到的,所以棱台的各侧棱延长后必须交于一点.
4.棱台的表示
可用上底面与下底面的顶点表示.
例如,如图所示的棱台ABCD-A′B′C′D′.
A
B
C
D
5.棱台的分类
按底面的形状分为三棱台(底面是三角形)、四棱台(底面是四边形)、……
正棱台:由正棱锥截得的棱台,其中正棱台上、下底面都是正多边形,两者中心的连线是棱台的高;
斜高
正四棱台
高
正棱台的侧面都全等,且都是等腰梯形,这些等腰梯形的高也都相等,称为棱台的斜高.
例2 如图所示是一个正三棱台,而且下底面边长为2,上底面边长和侧棱长都为1,O与O′分别是下底面和上底面的中心.
(1)求棱台的斜高;
(2)求棱台的高.
解:(1)因为是正三棱台,所以侧面都是全等的等腰梯形.
如图所示,在梯形ACC′A′中,分别过A′,C′作AC的垂线A′E与C′F,
则由 AC=2,AA′=A′C′=C′C=1 可知 ,
从而 ,即斜高为 .
因此:O′O 因此棱台的高为:
方法归纳:计算锥体和台体的表面积,注意四个基本量:底面边长、高、斜高、侧棱,并注意它们组成的直角三角形的应用.
O′
O
B′
B
H
在tB′中,B′H
(2)根据O与O′分别为下底面和上底面的中心,以及下底面边长和上底面的边长分别为2,1,可以算出:
连接O′B′与,过B′作B′H,则
棱锥、棱台的定义与几何特征;
棱锥、棱台的棱长、斜高与高之间的关系.
棱锥
棱台
正棱锥
正棱台
本节课你学到了哪些知识?
11.1.4 棱锥与棱台
1.了解棱锥、棱台的定义和结构特征
2.知道棱锥、棱台的表面积计算公式,能用公式解决简单的实际问题.(重点)
下图所示的建筑是什么几何体呢?你还能举出一些例子吗?
情景导入
思考1:观察下图,如何将棱柱变换成下方的几何体
方头方脑:棱柱
尖头窄脸:棱锥
知识点1: 棱锥
思考2:这些棱锥具有怎样的共性?你能归纳出一个几何体是棱台的充要条件是什么吗?
1.棱锥的定义
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体称为棱锥.
注意:其余各面必须要满足有一个公共顶点.
①底面是多边形
②侧面是三角形
③都有一个公共顶点
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
O
棱锥的高
(1)这个多边形面叫做棱锥的底面;
(2)有公共顶点的各个三角形面叫做棱锥的侧面;
(3)相邻两侧面的公共边叫做棱锥的侧棱;
(4)各侧面的公共顶点叫做棱锥的顶点.
(5)过棱锥的顶点作棱锥底面的垂线,所得到的线段(或它的长度)称为棱锥的高.
(6)棱锥所有侧面的面积之和称为棱锥的侧面积.
2.棱锥的元素
(1)用表示顶点和底面各顶点的字母表示,如棱锥S-ABCD.
(2)用表示顶点和底面的一条对角线端点的字母来表示,如棱锥S-AC.
S
A
B
C
D
3.棱锥的表示
4.棱锥的分类
棱锥的底面可以是
三角形、四边形、五边形……
把这样的棱锥分别叫做
三棱锥、四棱锥、五棱锥……
三棱锥 (四面体)
四棱锥
五棱锥
按底面边数分类
正棱椎:
如图,PO为棱锥P-ABCD的高,因此PO⊥面ABCD.
从而可知:
如果棱锥的底面是正多边形,且棱锥的顶点与底面中心的连线垂直于底面,则称这个棱锥为正棱锥.正棱锥的侧面都全等,而且都是等腰三角形,这些等腰三角形底边上的高也都相等,称为棱锥的斜高.
1.能保证棱锥是正棱锥的一个条件是( )
(A)底面为正多边形 (B)各侧棱都相等
(C)各侧面与底面都是全等的正三角形 (D)各侧面都是等腰三角形
C
例1 如图是底面边长为1且侧棱长为 的正六棱锥
(1)写出直线PA与直线CD,直线PA与面ABCDEF之间的关系;
(2)求棱锥的高和斜高;
(3)求棱锥的侧面积.
解:(1)直线PA与直线CD异面,直线PA∩面ABCDEF=A.
(2)作出棱锥的高PO,因为是正六棱锥,所以O是底面的中心,连接OC,可知OC=1.
在Rt△POC中,可知:
设BC的中点为M,由△PBC为等腰三角形可知,PM⊥MC ,
因此PM为斜高,从而
(3)因为△PBC的面积为:
故棱锥的侧面积为:
2.已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为 ,计算它的高和斜高.
因为底面正方形ABCD的面积是16,所以BC=4,MB=OM=2,
又因为VB= ,在Rt VOB中,由勾股定理得
在Rt△VOM中,由勾股定理得
即正四棱锥的高为6,斜高为
解:
知识点2:棱台
思考1:观察下图,如何将棱锥变换成下方的几何体
棱锥被平行于底面的平面所截,截面和底面间的多面体叫做棱台.
1.棱台的定义:
(1)原棱锥的底面与截面分别称为棱台的下底面和上底面,其余各面称为棱台的侧面;
(2)相邻两侧面的公共边称为棱台的侧棱.
(3)过棱台一个底面上的任意一个顶点,
作另一个底面的垂线所得到的线段(或它的长度)称为棱台的高.
上底面
侧面
侧棱
高
下底面
2.棱台的元素
3.棱台的性质:两底面是相似的多边形,侧棱的延长线交于一点.
思考2:下图中的几何体是不是棱台 为什么
不是.
因为棱台是用一个平行于棱锥底面的平面去截棱锥得到的,所以棱台的各侧棱延长后必须交于一点.
4.棱台的表示
可用上底面与下底面的顶点表示.
例如,如图所示的棱台ABCD-A′B′C′D′.
A
B
C
D
5.棱台的分类
按底面的形状分为三棱台(底面是三角形)、四棱台(底面是四边形)、……
正棱台:由正棱锥截得的棱台,其中正棱台上、下底面都是正多边形,两者中心的连线是棱台的高;
斜高
正四棱台
高
正棱台的侧面都全等,且都是等腰梯形,这些等腰梯形的高也都相等,称为棱台的斜高.
例2 如图所示是一个正三棱台,而且下底面边长为2,上底面边长和侧棱长都为1,O与O′分别是下底面和上底面的中心.
(1)求棱台的斜高;
(2)求棱台的高.
解:(1)因为是正三棱台,所以侧面都是全等的等腰梯形.
如图所示,在梯形ACC′A′中,分别过A′,C′作AC的垂线A′E与C′F,
则由 AC=2,AA′=A′C′=C′C=1 可知 ,
从而 ,即斜高为 .
因此:O′O 因此棱台的高为:
方法归纳:计算锥体和台体的表面积,注意四个基本量:底面边长、高、斜高、侧棱,并注意它们组成的直角三角形的应用.
O′
O
B′
B
H
在tB′中,B′H
(2)根据O与O′分别为下底面和上底面的中心,以及下底面边长和上底面的边长分别为2,1,可以算出:
连接O′B′与,过B′作B′H,则
棱锥、棱台的定义与几何特征;
棱锥、棱台的棱长、斜高与高之间的关系.
棱锥
棱台
正棱锥
正棱台
本节课你学到了哪些知识?
