11.1.5 旋转体 课件(共24张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.5 旋转体 课件(共24张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 15:33:37 | ||
图片预览





文档简介
(共24张PPT)
11.1.5 旋转体
1.了解圆柱、圆锥、圆台和球的有关概念.(重点)
2.理解圆柱、圆锥、圆台和球及其简单组合体的结构特征.
3.掌握圆柱、圆锥、圆台和球的相关性质.(难点)
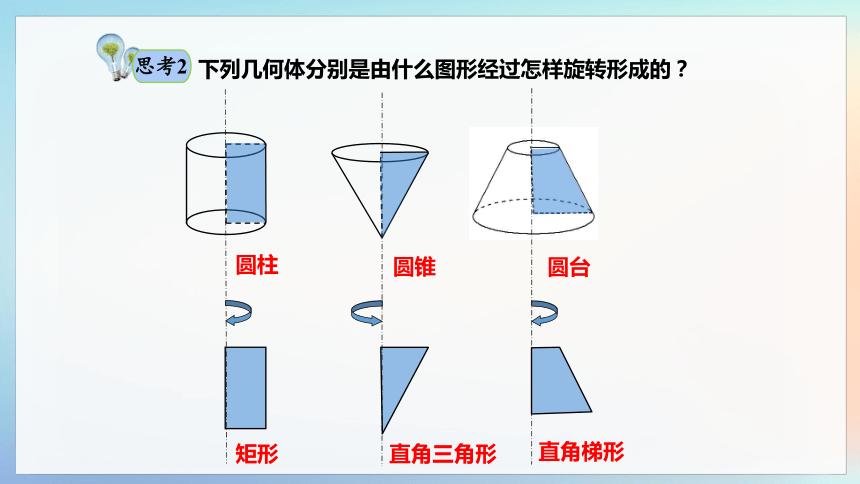
下面的几何体与多面体不同,仔细观察这些几何体,它们有什么共同特点或生成规律?
知识点1 圆柱、圆锥、圆台
思考1
直角三角形
直角梯形
圆柱
圆锥
圆台
矩形
下列几何体分别是由什么图形经过怎样旋转形成的?
思考2
圆柱O′O
圆锥SO
圆台O′O
1.圆柱、圆锥、圆台的定义:
分别以矩形的一边、直角三角形的一直角边、直角梯形中垂直于底边的腰所在的直线为旋转轴,将矩形、直角三角形、直角梯形分别旋转一周而形成的曲面所围成的几何体, 叫做圆柱,圆锥,圆台.
用类似圆柱、圆锥、圆台的围绕着旋转轴旋转形成方式构成的几何体都是旋转体.
圆柱
圆锥
圆台
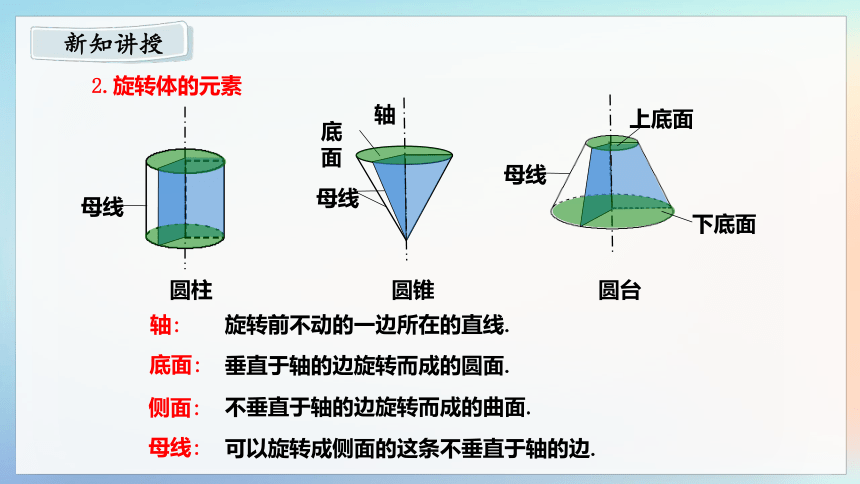
轴:
侧面:
底面
垂直于轴的边旋转而成的圆面.
不垂直于轴的边旋转而成的曲面.
母线:
可以旋转成侧面的这条不垂直于轴的边.
旋转前不动的一边所在的直线.
轴
底面:
母线
2.旋转体的元素
母线
母线
上底面
下底面
性质1:平行于底面的截面都是圆.
性质2:过轴的截面(轴截面)分别是全等的矩形、等腰三角形、等腰梯形.
1.平行于圆柱,圆锥,圆台的底面的截面是什么图形?
2.过圆柱、圆锥、圆台的旋转轴的截面是什么图形?
想一想
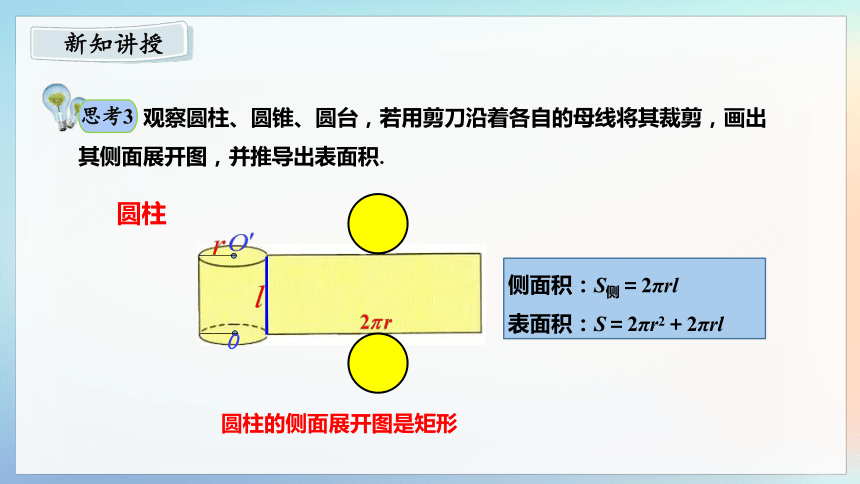
侧面积:S侧=2πrl
表面积:S=2πr2+2πrl
观察圆柱、圆锥、圆台,若用剪刀沿着各自的母线将其裁剪,画出
其侧面展开图,并推导出表面积.
圆柱的侧面展开图是矩形
O
圆柱
思考3
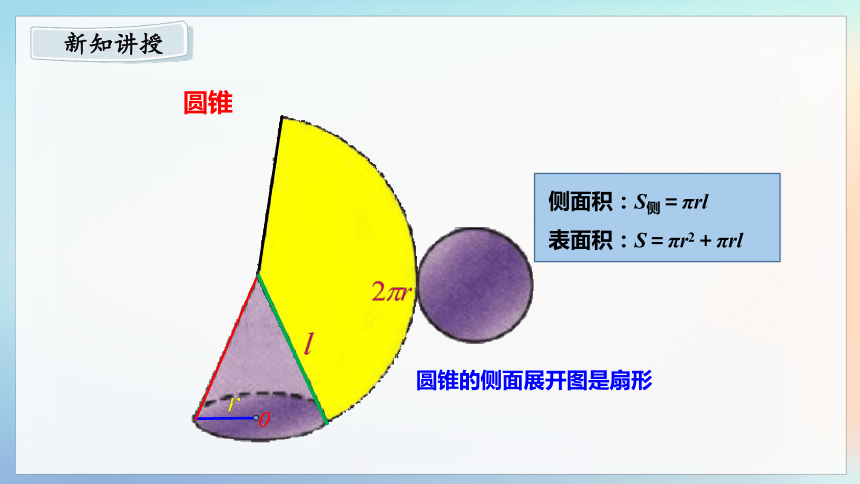
圆锥的侧面展开图是扇形
O
圆锥
侧面积:S侧=πrl
表面积:S=πr2+πrl
侧面积:S侧=π(r+r′)l
表面积:S=πr2+πr′2+π(r+r′)l
O
O′
圆台的侧面展开图是扇环
圆台
小扇形的半径: .
O
O′
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
r′=r
上底扩大
O
r′=0
上底缩小
O
S=πr2+πr′2+π(r+r′)l
S=πr2+πrl
S=2πr2+2πrl
思考
球
知识点2 球
圆可以看成平面上到定点的距离等于定长的点的集合,类比圆,球面上的点有怎样的性质?
球面可以看成空间中到一个定点的距离等于定长的点的集合;
半圆
球
球是由什么图形经过怎样旋转形成的?
思考1
思考2
球O
球面可以看作一个半圆绕着它的直径所在的直线旋转一周所形成的曲面,球面围成的几何体,叫做球.
轴
形成球的半圆的圆心叫球心,连接球面上一点和球心的线段叫球的半径,连接球面上两点且通过球心的线段叫球的直径.
1.球的定义:
用一个平面去截球体得到的截面是什么图形?
用一个平面去截球体得到的截面是一个圆面.
球面被经过球心的平面截得的圆叫做球的大圆;被不经过球心的平面截得的圆叫做球的小圆.
当用刀去切一个球形的西瓜时所得到的截面是什么形状?
想一想
2.球的截面性质:
用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.
若R:球的半径, r:截面圆的半径,d:球心到截面的距离,则
(球的半径、截面圆的半径和球心到截面的距离组成一个直角三角形)
R2=r2+d2
如图,用一个平面α去截半径为R的球O,截得的圆面的圆心为O′,OO′与平面α有什么位置关系?若OO′=d,O′P的长等于多少?
思考3
例2 把地球看成一个半径为6370km的球,已知我国首都北京靠近北纬40°,
求北纬40°纬线的长度( π≈3.1416,cos40°≈0.7660,结果精确到1km)
解:作出截面图,如图所示,
设A是北纬40°圈上的一点,AK是北纬40°圈的半径,O为球心,
所以OK⊥AK.
设北纬40°的纬线长为ckm,因为∠AOB=∠OAK=40°,
所以
即北纬40°的纬线长约为30658km.
例题讲解
3.球的表面积
柱、锥的表面都可展开放在平面内,这样我们就可以根据平面图形的性质,求它们的表面积.但球面不能展平成平面,我们要用其他方法求它的表面积:
分 割
近似求和
化为准确和
例3 已知一个长方体的8个顶点都在一个球面上,且长方体的棱长为3,4, 5,求球的表面积.
所以所求的球的表面积为:
分析:确定满足到长方体的8个顶点都相等的点即为球心.
解:由题设可知,长方体的体对角线的中点的就是球心,
又因为
例题讲解
.
已知一个正方体的棱长为2.正方体的八个顶点均在同一球面上,求此球的表面积.
所以正方体的外接球直径等于正方体的对角线长,即
∴球的表面积
解:正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图,
.
长方体、正方体与球切、接的常用结论:
①长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则
②正方体的棱长为a,则正方体的外接球的半径 ,正方体的内切球的半径为 ,球与正方体的各棱相切,则球的半径为
1.正方形绕其一条对角线所在直线旋转一周,所得几何体是( )
A.圆柱 B.圆锥
C.圆台 D.两个圆锥
D
2.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为________cm.
解:如图是圆锥的轴截面,
则SA=20 cm,∠ASO=30°,
∴AO=10 cm,SO= cm.
11.1.5 旋转体
1.了解圆柱、圆锥、圆台和球的有关概念.(重点)
2.理解圆柱、圆锥、圆台和球及其简单组合体的结构特征.
3.掌握圆柱、圆锥、圆台和球的相关性质.(难点)
下面的几何体与多面体不同,仔细观察这些几何体,它们有什么共同特点或生成规律?
知识点1 圆柱、圆锥、圆台
思考1
直角三角形
直角梯形
圆柱
圆锥
圆台
矩形
下列几何体分别是由什么图形经过怎样旋转形成的?
思考2
圆柱O′O
圆锥SO
圆台O′O
1.圆柱、圆锥、圆台的定义:
分别以矩形的一边、直角三角形的一直角边、直角梯形中垂直于底边的腰所在的直线为旋转轴,将矩形、直角三角形、直角梯形分别旋转一周而形成的曲面所围成的几何体, 叫做圆柱,圆锥,圆台.
用类似圆柱、圆锥、圆台的围绕着旋转轴旋转形成方式构成的几何体都是旋转体.
圆柱
圆锥
圆台
轴:
侧面:
底面
垂直于轴的边旋转而成的圆面.
不垂直于轴的边旋转而成的曲面.
母线:
可以旋转成侧面的这条不垂直于轴的边.
旋转前不动的一边所在的直线.
轴
底面:
母线
2.旋转体的元素
母线
母线
上底面
下底面
性质1:平行于底面的截面都是圆.
性质2:过轴的截面(轴截面)分别是全等的矩形、等腰三角形、等腰梯形.
1.平行于圆柱,圆锥,圆台的底面的截面是什么图形?
2.过圆柱、圆锥、圆台的旋转轴的截面是什么图形?
想一想
侧面积:S侧=2πrl
表面积:S=2πr2+2πrl
观察圆柱、圆锥、圆台,若用剪刀沿着各自的母线将其裁剪,画出
其侧面展开图,并推导出表面积.
圆柱的侧面展开图是矩形
O
圆柱
思考3
圆锥的侧面展开图是扇形
O
圆锥
侧面积:S侧=πrl
表面积:S=πr2+πrl
侧面积:S侧=π(r+r′)l
表面积:S=πr2+πr′2+π(r+r′)l
O
O′
圆台的侧面展开图是扇环
圆台
小扇形的半径: .
O
O′
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
r′=r
上底扩大
O
r′=0
上底缩小
O
S=πr2+πr′2+π(r+r′)l
S=πr2+πrl
S=2πr2+2πrl
思考
球
知识点2 球
圆可以看成平面上到定点的距离等于定长的点的集合,类比圆,球面上的点有怎样的性质?
球面可以看成空间中到一个定点的距离等于定长的点的集合;
半圆
球
球是由什么图形经过怎样旋转形成的?
思考1
思考2
球O
球面可以看作一个半圆绕着它的直径所在的直线旋转一周所形成的曲面,球面围成的几何体,叫做球.
轴
形成球的半圆的圆心叫球心,连接球面上一点和球心的线段叫球的半径,连接球面上两点且通过球心的线段叫球的直径.
1.球的定义:
用一个平面去截球体得到的截面是什么图形?
用一个平面去截球体得到的截面是一个圆面.
球面被经过球心的平面截得的圆叫做球的大圆;被不经过球心的平面截得的圆叫做球的小圆.
当用刀去切一个球形的西瓜时所得到的截面是什么形状?
想一想
2.球的截面性质:
用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.
若R:球的半径, r:截面圆的半径,d:球心到截面的距离,则
(球的半径、截面圆的半径和球心到截面的距离组成一个直角三角形)
R2=r2+d2
如图,用一个平面α去截半径为R的球O,截得的圆面的圆心为O′,OO′与平面α有什么位置关系?若OO′=d,O′P的长等于多少?
思考3
例2 把地球看成一个半径为6370km的球,已知我国首都北京靠近北纬40°,
求北纬40°纬线的长度( π≈3.1416,cos40°≈0.7660,结果精确到1km)
解:作出截面图,如图所示,
设A是北纬40°圈上的一点,AK是北纬40°圈的半径,O为球心,
所以OK⊥AK.
设北纬40°的纬线长为ckm,因为∠AOB=∠OAK=40°,
所以
即北纬40°的纬线长约为30658km.
例题讲解
3.球的表面积
柱、锥的表面都可展开放在平面内,这样我们就可以根据平面图形的性质,求它们的表面积.但球面不能展平成平面,我们要用其他方法求它的表面积:
分 割
近似求和
化为准确和
例3 已知一个长方体的8个顶点都在一个球面上,且长方体的棱长为3,4, 5,求球的表面积.
所以所求的球的表面积为:
分析:确定满足到长方体的8个顶点都相等的点即为球心.
解:由题设可知,长方体的体对角线的中点的就是球心,
又因为
例题讲解
.
已知一个正方体的棱长为2.正方体的八个顶点均在同一球面上,求此球的表面积.
所以正方体的外接球直径等于正方体的对角线长,即
∴球的表面积
解:正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图,
.
长方体、正方体与球切、接的常用结论:
①长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则
②正方体的棱长为a,则正方体的外接球的半径 ,正方体的内切球的半径为 ,球与正方体的各棱相切,则球的半径为
1.正方形绕其一条对角线所在直线旋转一周,所得几何体是( )
A.圆柱 B.圆锥
C.圆台 D.两个圆锥
D
2.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为________cm.
解:如图是圆锥的轴截面,
则SA=20 cm,∠ASO=30°,
∴AO=10 cm,SO= cm.
