11.2 平面的基本事实与推论 课件(共21张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.2 平面的基本事实与推论 课件(共21张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
11.2 平面的基本事实与推论
1.了解平面的概念,掌握平面的画法及表示方法.
2.掌握平面的基本事实及推论,能用符号语言描述空间点、直线、平面之间的位置关系.
3.能用图形、文字、符号三种语言描述三个基本事实,并能解决空间线面的位置关系问题.
情景导入
在初中,我们学习过直线,回忆一下直线有哪些特征?观察下面三个“平面”,思考一下平面应该具有哪些特征?
直线很“直”且“无限延伸
类似地,平面很“平”
且“无限延展
欧几里得
平面是一个表面,上面贴合着很多直线
海伦
平面是直线恰好与相合的表面并且是笔直延展的
希尔伯特
平面无大小,无厚度,可无限延展
莱布尼茨
平面是点的几何,与两个定点的距离相等
观察以下几位数学家对平面的定义并思考,我们可以通过哪些数学元素来研究平面?
情景导入
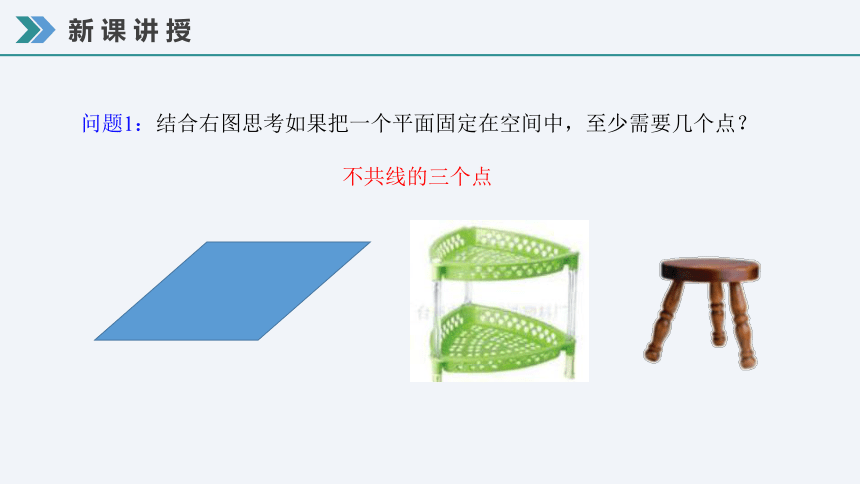
问题1:结合右图思考如果把一个平面固定在空间中,至少需要几个点?
不共线的三个点
基本事实1:
经过不在一条直线上的三个点,有且只有一个平面。
不共线的三个点A、B、C,
问题2:结合图片思考,直线上至少已知几点在某平面内时,就能确保该直线在该平面内?
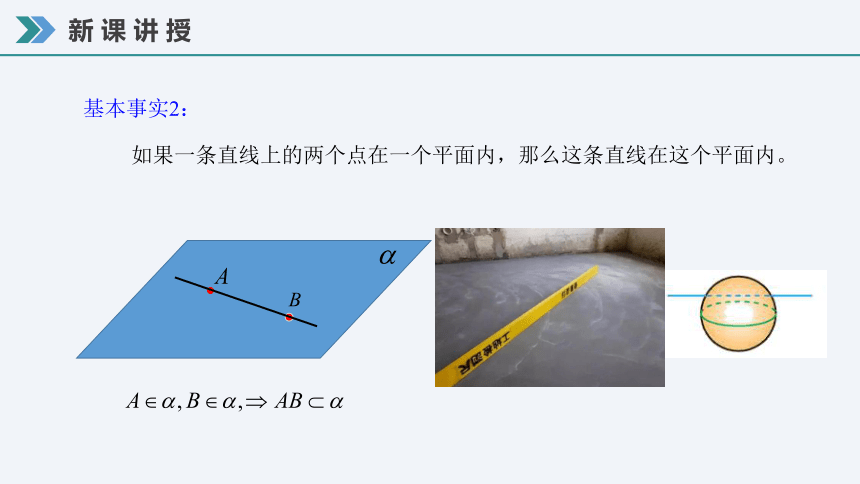
基本事实2:
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内。
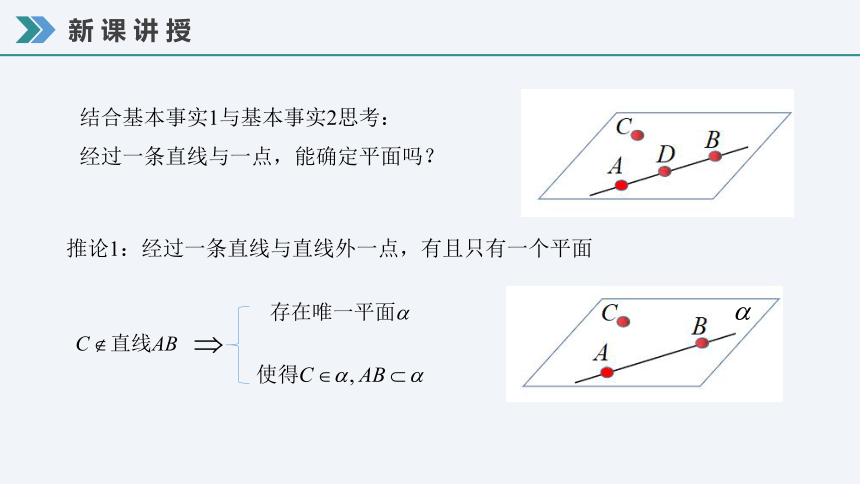
结合基本事实1与基本事实2思考:
经过一条直线与一点,能确定平面吗?
推论1:经过一条直线与直线外一点,有且只有一个平面
如图,把三角尺的一个角立在课桌上,三角尺所在平面与课桌面所在平面是否只相交于点B 为什么?
基本事实3:
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
下图是一张倒置的凳子,你能用所学知识检查一下凳子的四条腿的末端是否在同一平面内?
推论2:经过两条相交直线,有且只有一个平面
推论3:经过两条平行直线,有且只有一个平面
推论:
推理2:经过两条相交直线,有且只有一个平面。
推理3:经过两条平行直线,有且只有一个平面。
1、判断正误.
(1)三点可以确定一个平面。
(2)一条直线和直线外一点可以确定一个平面。
(3)四边形是平面图形。
(4)两条不重合的直线可以确定一个平面。
练一练
M
N
H
证明:
问题3:
已知三条直线a、b、c两两相交,且不共点
求证:a、b、c三线共面
问题4:
解:因为A∈面D1AE,A∈面ABCD,所以面D1AE∩ABCD,
即面D1AE与面ABCD相交.
延长D1E与DC,设它们相交于F,
如图所示,则:
F∈直线D1E,直线D1E 面D1AE,
F∈直线DC,直线DC 面ABCD,
则F∈面D1AE∩面ABCD,从而AF为面D1AE与面ABCD的交线,如图所示.
基本事实
基本事实1
推论2
推论3
推论1
基本事实2
基本事实3
推论
基本事实1
推论2
推论3
推论1
基本事实2
基本事实3
确定平面
线面关系
面面关系
三种语言
图形语言
文字语言
符号语言
新知识的应用
今天我们学习了什么?
1.在下列各种面中,不能被认为是平面的一部分的是( )
A.黑板面
B.乒乓球桌面
C.篮球的表面
D.平静的水面
C
2.
11.2 平面的基本事实与推论
1.了解平面的概念,掌握平面的画法及表示方法.
2.掌握平面的基本事实及推论,能用符号语言描述空间点、直线、平面之间的位置关系.
3.能用图形、文字、符号三种语言描述三个基本事实,并能解决空间线面的位置关系问题.
情景导入
在初中,我们学习过直线,回忆一下直线有哪些特征?观察下面三个“平面”,思考一下平面应该具有哪些特征?
直线很“直”且“无限延伸
类似地,平面很“平”
且“无限延展
欧几里得
平面是一个表面,上面贴合着很多直线
海伦
平面是直线恰好与相合的表面并且是笔直延展的
希尔伯特
平面无大小,无厚度,可无限延展
莱布尼茨
平面是点的几何,与两个定点的距离相等
观察以下几位数学家对平面的定义并思考,我们可以通过哪些数学元素来研究平面?
情景导入
问题1:结合右图思考如果把一个平面固定在空间中,至少需要几个点?
不共线的三个点
基本事实1:
经过不在一条直线上的三个点,有且只有一个平面。
不共线的三个点A、B、C,
问题2:结合图片思考,直线上至少已知几点在某平面内时,就能确保该直线在该平面内?
基本事实2:
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内。
结合基本事实1与基本事实2思考:
经过一条直线与一点,能确定平面吗?
推论1:经过一条直线与直线外一点,有且只有一个平面
如图,把三角尺的一个角立在课桌上,三角尺所在平面与课桌面所在平面是否只相交于点B 为什么?
基本事实3:
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
下图是一张倒置的凳子,你能用所学知识检查一下凳子的四条腿的末端是否在同一平面内?
推论2:经过两条相交直线,有且只有一个平面
推论3:经过两条平行直线,有且只有一个平面
推论:
推理2:经过两条相交直线,有且只有一个平面。
推理3:经过两条平行直线,有且只有一个平面。
1、判断正误.
(1)三点可以确定一个平面。
(2)一条直线和直线外一点可以确定一个平面。
(3)四边形是平面图形。
(4)两条不重合的直线可以确定一个平面。
练一练
M
N
H
证明:
问题3:
已知三条直线a、b、c两两相交,且不共点
求证:a、b、c三线共面
问题4:
解:因为A∈面D1AE,A∈面ABCD,所以面D1AE∩ABCD,
即面D1AE与面ABCD相交.
延长D1E与DC,设它们相交于F,
如图所示,则:
F∈直线D1E,直线D1E 面D1AE,
F∈直线DC,直线DC 面ABCD,
则F∈面D1AE∩面ABCD,从而AF为面D1AE与面ABCD的交线,如图所示.
基本事实
基本事实1
推论2
推论3
推论1
基本事实2
基本事实3
推论
基本事实1
推论2
推论3
推论1
基本事实2
基本事实3
确定平面
线面关系
面面关系
三种语言
图形语言
文字语言
符号语言
新知识的应用
今天我们学习了什么?
1.在下列各种面中,不能被认为是平面的一部分的是( )
A.黑板面
B.乒乓球桌面
C.篮球的表面
D.平静的水面
C
2.
