11.3.1 平行直线与异面直线 课件(共21张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.3.1 平行直线与异面直线 课件(共21张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
11.3.1 平行直线与异面直线
1.掌握空间直线的平行公理.(重点)
2.掌握等角定理以及平移和空间四边形的定义.(难点)
3.理解异面直线的概念,会判断两条直线是否异面.(重点)
情景导入
想一想:
(1)折纸的折痕之间、路灯杆所在的直线具有怎样的关系?
(2)对于空间中的两条直线,它们有怎样的位置关系?
知识点1 平行直线
“过直线外一点有且只有一条直线与已知直线平行”在空间中是否仍成立?
平行公理:过直线外一点有且只有一条直线与已知直线平行.
成立
思考1
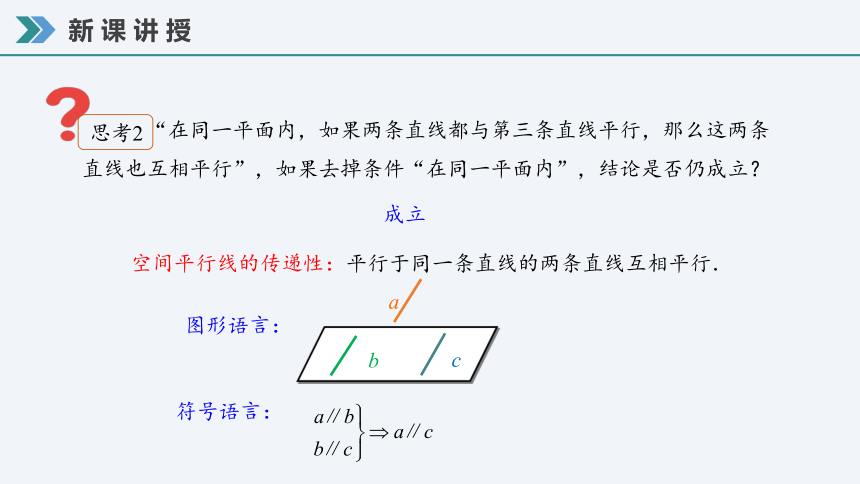
“在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也互相平行”,如果去掉条件“在同一平面内”,结论是否仍成立?
成立
空间平行线的传递性:平行于同一条直线的两条直线互相平行.
图形语言:
符号语言:
a
b
c
思考2
由空间平行线的传递性可以得到几何体中的一些线线平行关系.
例如,如图所示的棱柱中,因为侧面都是平行四边形,所以有:
如图所示,在三棱锥S MNP中,E,F,G,H分别是棱SN、SP、MN、MP的中点,则EF与HG的位置关系是 .
平行
解析: ∵E,F分别是SN和SP的中点,∴EF∥PN.同理可证HG∥PN,∴EF∥HG.
练一练
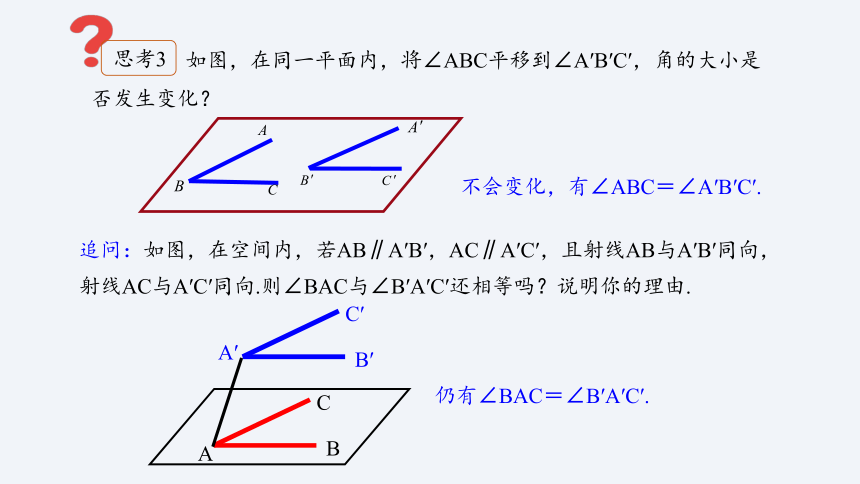
不会变化,有∠ABC=∠A′B′C′.
追问:如图,在空间内,若AB∥A′B′,AC∥A′C′,且射线AB与A′B′同向,射线AC与A′C′同向.则∠BAC与∠B′A′C′还相等吗?说明你的理由.
C′
B
C
A
B′
A′
仍有∠BAC=∠B′A′C′.
如图,在同一平面内,将∠ABC平移到∠A′B′C′,角的大小是否发生变化?
思考3
证明:在AB上取一点E,在A'B'上取一点E',使得AE=A'E';在AC上取一点F,在A'C'上取一点F',使得AF=A'F';
∵AEA'E'且 AE=A'E' ,∴AEE'A'是一个平行四边形,∴ ,
同理
由空间平行线的传递性可知 ,
∴EFF'E'是一个平行四边形,∴EF=E'F';
于是有 ,从而∠EAF=∠E'A'F'.
F'
E'
E
F
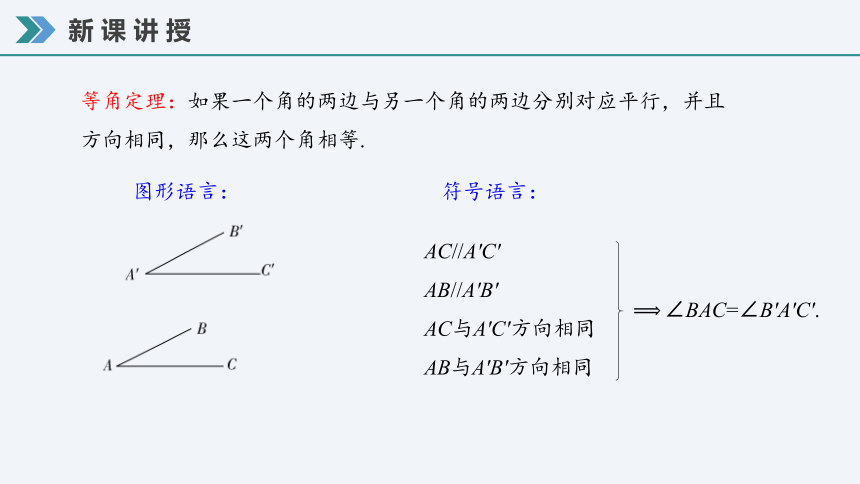
等角定理:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
图形语言:
AC//A'C'
AB//A'B'
AC与A′C′方向相同
AB与A′B′方向相同
∠BAC=∠B′A′C′.
符号语言:
m
图2
l
l
m
P
图1
从图中可见,直线 与既不相交,也不平行.
空间中直线之间的这种关系称为异面直线.
如图,直线与直线有怎样的位置关系?
知识点2 异面直线
两条直线不能同时在任何一个平面内
1.异面直线的定义
思考1
为了表示异面直线,不共面的特点,作图时,通常用一个或两个平面来衬托,如图所示.
2.异面直线的画法
(1)两图中直线m和l是异面直线吗
α
β
l
m
m
l
(2 ,则与是异面直线吗?
不一定
不是
(3)如何判断两条直线是异面直线?
思考2
这是因为同时通过直线与点的平面只能是(过一条直线与直线外一点有且只有一个平面),如果与直线是共面的,则,这与矛盾.
与一个平面相交于一点的直线与这个平面内不经过交点的直线异面.
3.异面直线的判定
判定两条直线是异面直线的方法:①定义法,②定理法,③反证法.
③
如图,点P,Q,R,S分别是正方体的四条棱的中点,则直线PQ与RS是异面直线的图是 .
练一练
(1)相交
(2)平行
只有一个公共点
没有公共点
在同一平面
总结:空间中两直线的三种位置关系
(3)异面直线
没有公共点
不同在任一平面
m
P
l
C
A
B
D
如图,将平面四边形ABCD沿着BD折起来,得到怎样的图形?
A
C
D
B
知识点3 空间四边形
思考1
像折后的空间图形ABCD这样,顺次连接不共面
的四点A,B,C,D所构成的图形,叫做空间四边形.
这四个点中的各个点叫做空间四边形的顶点;
所连接的相邻顶点间的线段叫做空间四边形的边;
连接不相邻的顶点的线段叫做空间四边形的对角线.
1.空间四边形的定义
2.空间四边形的元素
A
C
D
B
A
C
D
B
四条边
对角线
空间四边形用表示顶点的四个字母表示,如下图中的四边形可以表示为空间四边形ABCD,线段AB,BC,CD,DA是它的四条边,线段AC,BD是它的对角线.
3.空间四边形的表示
例 如图所示的空间四边形ABCD中,E,F,G,H分别是边AB,AD,BC,CD的中点,求证:四边形EFHG是平行四边形.
证明:在△ABC中,因为E,F分别是AB,AD的中点,所以由三角形的中位线定理可知
且 ,
同理, 且
因此 ,所以四边形EFGH是平行四边形.
已知四边形 ABCD是空间四边形, E,H分别是边AB ,AD 的中点, F,G分别是边CB,CD上的点,且 ,求证:四边形 EFGH是梯形.
证明:
练一练
11.3.1 平行直线与异面直线
1.掌握空间直线的平行公理.(重点)
2.掌握等角定理以及平移和空间四边形的定义.(难点)
3.理解异面直线的概念,会判断两条直线是否异面.(重点)
情景导入
想一想:
(1)折纸的折痕之间、路灯杆所在的直线具有怎样的关系?
(2)对于空间中的两条直线,它们有怎样的位置关系?
知识点1 平行直线
“过直线外一点有且只有一条直线与已知直线平行”在空间中是否仍成立?
平行公理:过直线外一点有且只有一条直线与已知直线平行.
成立
思考1
“在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也互相平行”,如果去掉条件“在同一平面内”,结论是否仍成立?
成立
空间平行线的传递性:平行于同一条直线的两条直线互相平行.
图形语言:
符号语言:
a
b
c
思考2
由空间平行线的传递性可以得到几何体中的一些线线平行关系.
例如,如图所示的棱柱中,因为侧面都是平行四边形,所以有:
如图所示,在三棱锥S MNP中,E,F,G,H分别是棱SN、SP、MN、MP的中点,则EF与HG的位置关系是 .
平行
解析: ∵E,F分别是SN和SP的中点,∴EF∥PN.同理可证HG∥PN,∴EF∥HG.
练一练
不会变化,有∠ABC=∠A′B′C′.
追问:如图,在空间内,若AB∥A′B′,AC∥A′C′,且射线AB与A′B′同向,射线AC与A′C′同向.则∠BAC与∠B′A′C′还相等吗?说明你的理由.
C′
B
C
A
B′
A′
仍有∠BAC=∠B′A′C′.
如图,在同一平面内,将∠ABC平移到∠A′B′C′,角的大小是否发生变化?
思考3
证明:在AB上取一点E,在A'B'上取一点E',使得AE=A'E';在AC上取一点F,在A'C'上取一点F',使得AF=A'F';
∵AEA'E'且 AE=A'E' ,∴AEE'A'是一个平行四边形,∴ ,
同理
由空间平行线的传递性可知 ,
∴EFF'E'是一个平行四边形,∴EF=E'F';
于是有 ,从而∠EAF=∠E'A'F'.
F'
E'
E
F
等角定理:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
图形语言:
AC//A'C'
AB//A'B'
AC与A′C′方向相同
AB与A′B′方向相同
∠BAC=∠B′A′C′.
符号语言:
m
图2
l
l
m
P
图1
从图中可见,直线 与既不相交,也不平行.
空间中直线之间的这种关系称为异面直线.
如图,直线与直线有怎样的位置关系?
知识点2 异面直线
两条直线不能同时在任何一个平面内
1.异面直线的定义
思考1
为了表示异面直线,不共面的特点,作图时,通常用一个或两个平面来衬托,如图所示.
2.异面直线的画法
(1)两图中直线m和l是异面直线吗
α
β
l
m
m
l
(2 ,则与是异面直线吗?
不一定
不是
(3)如何判断两条直线是异面直线?
思考2
这是因为同时通过直线与点的平面只能是(过一条直线与直线外一点有且只有一个平面),如果与直线是共面的,则,这与矛盾.
与一个平面相交于一点的直线与这个平面内不经过交点的直线异面.
3.异面直线的判定
判定两条直线是异面直线的方法:①定义法,②定理法,③反证法.
③
如图,点P,Q,R,S分别是正方体的四条棱的中点,则直线PQ与RS是异面直线的图是 .
练一练
(1)相交
(2)平行
只有一个公共点
没有公共点
在同一平面
总结:空间中两直线的三种位置关系
(3)异面直线
没有公共点
不同在任一平面
m
P
l
C
A
B
D
如图,将平面四边形ABCD沿着BD折起来,得到怎样的图形?
A
C
D
B
知识点3 空间四边形
思考1
像折后的空间图形ABCD这样,顺次连接不共面
的四点A,B,C,D所构成的图形,叫做空间四边形.
这四个点中的各个点叫做空间四边形的顶点;
所连接的相邻顶点间的线段叫做空间四边形的边;
连接不相邻的顶点的线段叫做空间四边形的对角线.
1.空间四边形的定义
2.空间四边形的元素
A
C
D
B
A
C
D
B
四条边
对角线
空间四边形用表示顶点的四个字母表示,如下图中的四边形可以表示为空间四边形ABCD,线段AB,BC,CD,DA是它的四条边,线段AC,BD是它的对角线.
3.空间四边形的表示
例 如图所示的空间四边形ABCD中,E,F,G,H分别是边AB,AD,BC,CD的中点,求证:四边形EFHG是平行四边形.
证明:在△ABC中,因为E,F分别是AB,AD的中点,所以由三角形的中位线定理可知
且 ,
同理, 且
因此 ,所以四边形EFGH是平行四边形.
已知四边形 ABCD是空间四边形, E,H分别是边AB ,AD 的中点, F,G分别是边CB,CD上的点,且 ,求证:四边形 EFGH是梯形.
证明:
练一练
