11.3.2 直线与平面平行 课件(共23张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.3.2 直线与平面平行 课件(共23张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 815.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
11.3.2 直线与平面平行
1.掌握直线与平面平行的判定定理和性质定理,能利用以上定理解决空间中的相关平行问题.
线
面
位
置
关
系
特征
图形表示
符号表示
内容
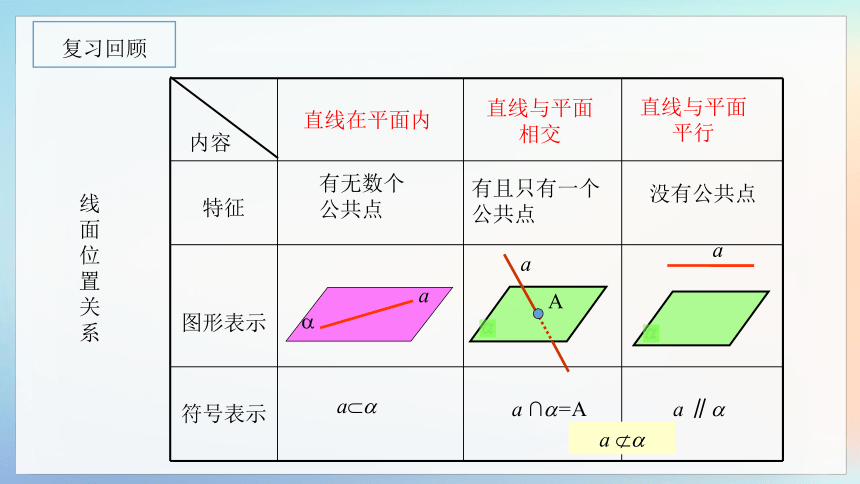
直线在平面内
直线与平面相交
直线与平面平行
有无数个
公共点
有且只有一个
公共点
没有公共点
a
a
A
a
a
a ∩ =A
a ∥
a
复习回顾
将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?
A
B
C
D
从中你能得出什么结论?
如何判断线面平行?
思考1
(一)线面平行判定定理
猜想:
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
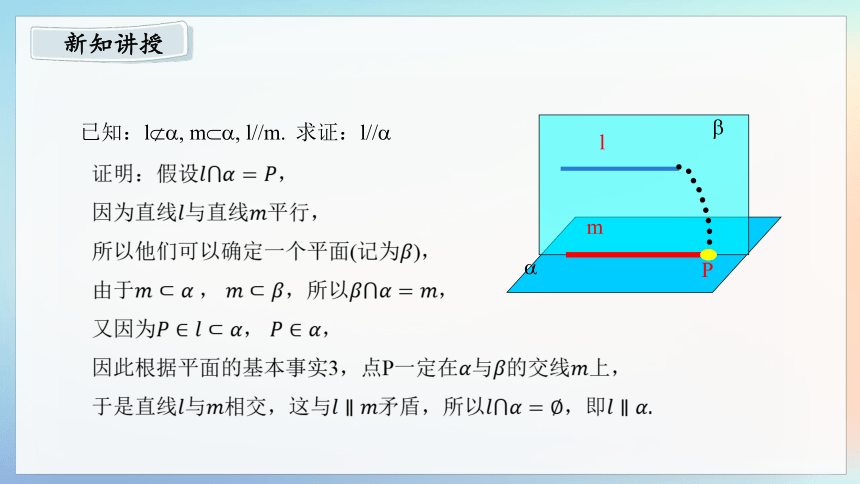
已知:l m l//m.
求证:l//
l
m
P
证明:假设,
因为直线与直线平行,
所以他们可以确定一个平面(记为),
由于, 所以,
又因为, ,
因此根据平面的基本事实3,点P一定在与的交线上,
于是直线与相交,这与 矛盾,所以,即
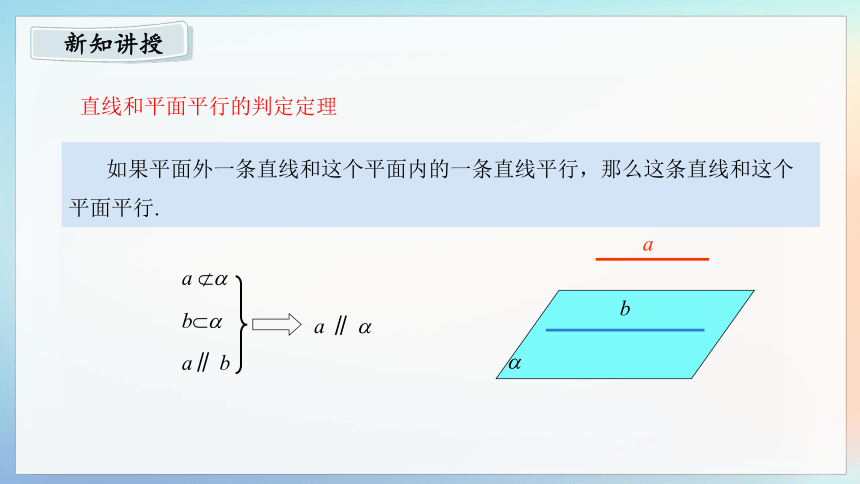
直线和平面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
b
a∥ b
a
a ∥
b
a
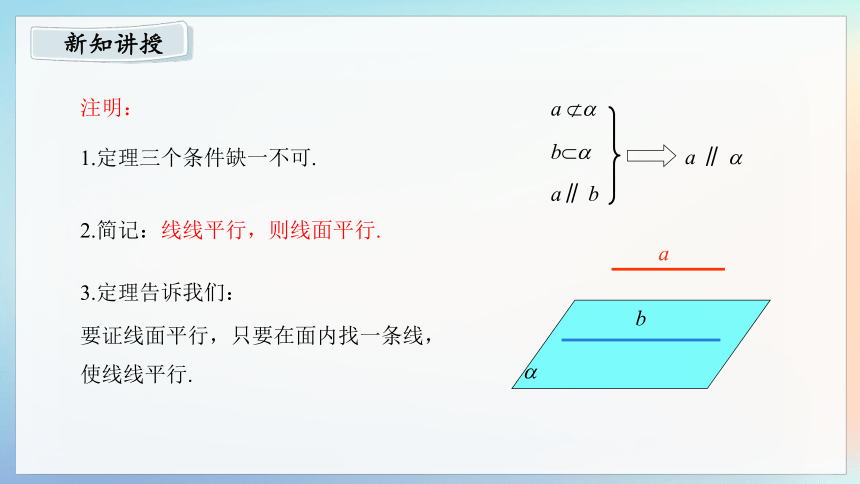
注明:
1.定理三个条件缺一不可.
2.简记:线线平行,则线面平行.
3.定理告诉我们:
要证线面平行,只要在面内找一条线,使线线平行.
b
a
b
a∥ b
a
a ∥
1.判断:对的打“√”,错的打“×”.
(1)若直线a与平面α内无数条直线平行,则a∥α.( )
(2)若直线l∥平面α,则l与平面α内的任意一条直线都不相交. ( )
(3)若直线a∥平面α,直线a∥直线b,则直线b∥平面α. ( )
(4)若直线a,b和平面α满足a∥α,b∥α,则a∥b. ( )
×
√
×
×
提示:(1)×.若直线a与平面α内无数条直线平行,则这条直线可能在这个平面内,也可能与这个平面平行,所以该命题错误.
(2)√.若直线l∥平面α,则l与平面α无公共点,所以l与平面α内的任意一条直线都不相交.
(3)×.直线b有可能在平面α内.
(4)×.若直线a,b和平面α满足a∥α,b∥α,则a与b平行、相交和异面都有可能.
例1 已知:空间四边形ABCD,E、F分别是AB、AD的中点,
求证:EF∥平面BCD
A
B
C
D
E
F
证明:连接BD,
∵E、F分别是AB、AD的中点,
∴EF ∥ BD
∴EF ∥平面BCD
BD 平面BCD
∩
在△ ABD中
又∵EF 平面BCD,
练习1 如图,在三棱锥P-ABC中,O,D分别是AC,PC的中点.
求证:OD∥平面PAB.
证明:在△ACP中,
∵O为AC的中点,D为PC的中点
∴OD∥AP.
∵OD 平面PAB,AP 平面PAB,
∴OD∥平面PAB.
练习2 如图,P是平行四边形ABCD所在平面外一点,E,F分别是AB,PD的中点. 求证:AF∥平面PCE.
练习3 已知有公共边AB的两个全等的矩形ABCD和ABEF不同在一个平面内,
P,Q分别是对角线AE,BD上的点,且AP=DQ.求证:PQ∥平面CBE.
练习3 已知有公共边AB的两个全等的矩形ABCD和ABEF不同在一个平面内,
P,Q分别是对角线AE,BD上的点,且AP=DQ.求证:PQ∥平面CBE.
平行关系的传递性
三角形中位线
平行四边形
平行线分线段成比例
方法小结
(二)线面平行性质定理
(1)如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?
(2)已知直线 a∥平面α,如何在平面α内找出和直线a 平行的一条直线?
思考2
m
l
证明:因为, 与没有公共点,
又因为,所以,
注意到且
所以与共面且没有公共点,即
直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
m
l
例2.如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PBC∩平面PAD=l.
(1)l与BC是否平行?说明理由;
(2)MN与平面PAD是否平行?试证明你的结论.
解: (1)平行,理由如下:
因为BC∥AD,BC 平面PAD,
AD 平面PAD,所以BC∥平面PAD.
又平面PBC∩平面PAD=l,BC 平面PBC,
所以BC∥l.
例2.如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PBC∩平面PAD=l.
(2)MN与平面PAD是否平行?试证明你的结论.
E
练习4 如图,AB是圆O的直径,点C是圆O上异于A,B的点,P为平面ABC外一点,E,F分别是PA,PC的中点.记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
解: 直线l∥平面PAC,证明如下:
因为E,F分别是PA,PC的中点,所以EF∥AC.
又EF 平面ABC,且AC 平面ABC,所以EF∥平面ABC.
而EF 平面BEF,且平面BEF∩平面ABC=l,
所以EF∥l.
因为l 平面PAC,EF 平面PAC,所以l∥平面PAC.
本节课你学到了哪些知识?
11.3.2 直线与平面平行
1.掌握直线与平面平行的判定定理和性质定理,能利用以上定理解决空间中的相关平行问题.
线
面
位
置
关
系
特征
图形表示
符号表示
内容
直线在平面内
直线与平面相交
直线与平面平行
有无数个
公共点
有且只有一个
公共点
没有公共点
a
a
A
a
a
a ∩ =A
a ∥
a
复习回顾
将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?
A
B
C
D
从中你能得出什么结论?
如何判断线面平行?
思考1
(一)线面平行判定定理
猜想:
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
已知:l m l//m.
求证:l//
l
m
P
证明:假设,
因为直线与直线平行,
所以他们可以确定一个平面(记为),
由于, 所以,
又因为, ,
因此根据平面的基本事实3,点P一定在与的交线上,
于是直线与相交,这与 矛盾,所以,即
直线和平面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
b
a∥ b
a
a ∥
b
a
注明:
1.定理三个条件缺一不可.
2.简记:线线平行,则线面平行.
3.定理告诉我们:
要证线面平行,只要在面内找一条线,使线线平行.
b
a
b
a∥ b
a
a ∥
1.判断:对的打“√”,错的打“×”.
(1)若直线a与平面α内无数条直线平行,则a∥α.( )
(2)若直线l∥平面α,则l与平面α内的任意一条直线都不相交. ( )
(3)若直线a∥平面α,直线a∥直线b,则直线b∥平面α. ( )
(4)若直线a,b和平面α满足a∥α,b∥α,则a∥b. ( )
×
√
×
×
提示:(1)×.若直线a与平面α内无数条直线平行,则这条直线可能在这个平面内,也可能与这个平面平行,所以该命题错误.
(2)√.若直线l∥平面α,则l与平面α无公共点,所以l与平面α内的任意一条直线都不相交.
(3)×.直线b有可能在平面α内.
(4)×.若直线a,b和平面α满足a∥α,b∥α,则a与b平行、相交和异面都有可能.
例1 已知:空间四边形ABCD,E、F分别是AB、AD的中点,
求证:EF∥平面BCD
A
B
C
D
E
F
证明:连接BD,
∵E、F分别是AB、AD的中点,
∴EF ∥ BD
∴EF ∥平面BCD
BD 平面BCD
∩
在△ ABD中
又∵EF 平面BCD,
练习1 如图,在三棱锥P-ABC中,O,D分别是AC,PC的中点.
求证:OD∥平面PAB.
证明:在△ACP中,
∵O为AC的中点,D为PC的中点
∴OD∥AP.
∵OD 平面PAB,AP 平面PAB,
∴OD∥平面PAB.
练习2 如图,P是平行四边形ABCD所在平面外一点,E,F分别是AB,PD的中点. 求证:AF∥平面PCE.
练习3 已知有公共边AB的两个全等的矩形ABCD和ABEF不同在一个平面内,
P,Q分别是对角线AE,BD上的点,且AP=DQ.求证:PQ∥平面CBE.
练习3 已知有公共边AB的两个全等的矩形ABCD和ABEF不同在一个平面内,
P,Q分别是对角线AE,BD上的点,且AP=DQ.求证:PQ∥平面CBE.
平行关系的传递性
三角形中位线
平行四边形
平行线分线段成比例
方法小结
(二)线面平行性质定理
(1)如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?
(2)已知直线 a∥平面α,如何在平面α内找出和直线a 平行的一条直线?
思考2
m
l
证明:因为, 与没有公共点,
又因为,所以,
注意到且
所以与共面且没有公共点,即
直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
m
l
例2.如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PBC∩平面PAD=l.
(1)l与BC是否平行?说明理由;
(2)MN与平面PAD是否平行?试证明你的结论.
解: (1)平行,理由如下:
因为BC∥AD,BC 平面PAD,
AD 平面PAD,所以BC∥平面PAD.
又平面PBC∩平面PAD=l,BC 平面PBC,
所以BC∥l.
例2.如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PBC∩平面PAD=l.
(2)MN与平面PAD是否平行?试证明你的结论.
E
练习4 如图,AB是圆O的直径,点C是圆O上异于A,B的点,P为平面ABC外一点,E,F分别是PA,PC的中点.记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
解: 直线l∥平面PAC,证明如下:
因为E,F分别是PA,PC的中点,所以EF∥AC.
又EF 平面ABC,且AC 平面ABC,所以EF∥平面ABC.
而EF 平面BEF,且平面BEF∩平面ABC=l,
所以EF∥l.
因为l 平面PAC,EF 平面PAC,所以l∥平面PAC.
本节课你学到了哪些知识?
