10.1.1 复数的概念 课件(共15张PPT) 2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 10.1.1 复数的概念 课件(共15张PPT) 2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 422.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 09:56:55 | ||
图片预览





文档简介
(共15张PPT)
10.1.1 复数的概念
1.了解复数的意义.
2.掌握有关复数的概念、复数的分类,初步掌握虚数单位的概念和性质.(重点)
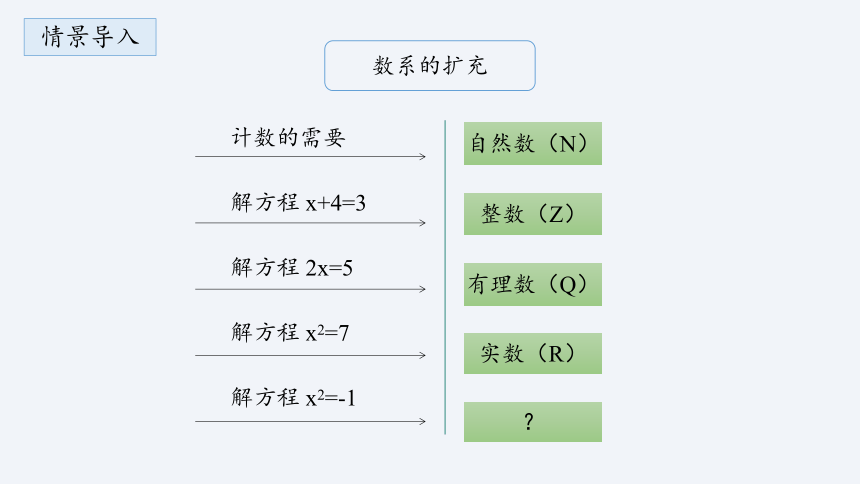
数系的扩充
计数的需要
自然数(N)
解方程 x+4=3
整数(Z)
解方程 2x=5
有理数(Q)
解方程 x2=7
实数(R)
解方程 x2=-1
?
情景导入
卡当生于1501年9月,他的数学贡献表现在他对算术和代数的研究,他在1545年出版了《大术》.该书系统给出代数学中的许多新概念和新方法;并著有《博奕论》一书,成为概率论的奠基者.在代数学上的一个重要贡献,是认真地引入了虚数,并接受虚数是方程式的根.
1873年,我国数学家华蘅芳将 “复数”引入中国!
情景导入
一般地,为了使方程=1有解,人们规定的平方等于=1,称为虚数单位。
所以方程 =-1的解为=或=-。
1.虚数的定义
例:解方程x =-2
解方程(x+1) =-2
说明:
(1)实数与i可以进行加法和乘法运算:
实数a与数i相加记为:a+i
实数b与数i相乘记为:bi ,并规定0 i =0
实数a与 bi相加记为:a+bi
(2)实数与 i 进行四则运算时,原有的加法、乘法运算律仍然成立.
z=a+bi(a,b∈R)
实部
虚部
虚数单位
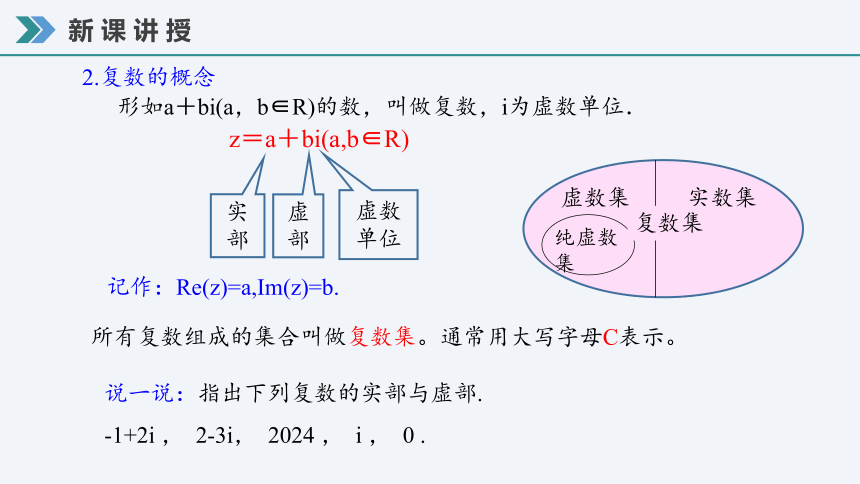
形如a+bi(a,b∈R)的数,叫做复数,i为虚数单位.
所有复数组成的集合叫做复数集。通常用大写字母C表示。
2.复数的概念
实数集
虚数集
纯虚数集
复数集
记作:Re(z)=a,Im(z)=b.
说一说:指出下列复数的实部与虚部.
-1+2i , 2-3i, 2024 , i , 0 .
3.复数的分类
复数集C和实数集R之间有什么关系?
想一想
例1 分别求实数x的取值,使得复数z=(x-2)+(x+3)i
(1)是实数;(2)是虚数;(3)是纯虚数.
解:(1)当x+3=0,即x=-3时,复数z是实数.
(2)当x+3≠0,即x≠-3时,复数z是虚数.
(3)当x-2=0,且x+3≠0,即x=2时,复数z是纯虚数.
1.若a=0,则z=a+bi (a ∈ R、b ∈ R)为纯虚数.
2.若z=a+bi (a ∈ R、b ∈ R)为纯虚数,则a=0.
故a=0是z=a+bi (a ∈ R、b ∈ R)为纯虚数的
条件.
判一判
4.复数的相等
复数相等:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注:
2) 一般来说,两个复数只能说相等或不相等,而不能比较大小.
1)
例2 分别求满足下列关系式的实数与的值
(1);
(2)
解:(1)根据复数相等的定义,得
(2)根据复数等于0得充要条件,得
解这个方程组,得
解这个方程组,得
例3 已知关于x的方程x2+(1-2i)x+(3m-i)=0有实根,求实数m的值.
2.4-3a-a2i=a2+4ai,则实数a的值为( )
A.1 B.1或-4 C.-4 D.0或-4
C
1.若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为( )
A.1 B.2 C.1或2 D.-1
B
虚数的引入
复 数
复数的分类
复数的相等
z = a + bi
(a,b∈R)
当b=0时z为实数;
当b 0时z为虚数;
(此时,当a =0时z为纯虚数).
a=c
b=d
a+bi=c+di
(a,b,c,d R)
10.1.1 复数的概念
1.了解复数的意义.
2.掌握有关复数的概念、复数的分类,初步掌握虚数单位的概念和性质.(重点)
数系的扩充
计数的需要
自然数(N)
解方程 x+4=3
整数(Z)
解方程 2x=5
有理数(Q)
解方程 x2=7
实数(R)
解方程 x2=-1
?
情景导入
卡当生于1501年9月,他的数学贡献表现在他对算术和代数的研究,他在1545年出版了《大术》.该书系统给出代数学中的许多新概念和新方法;并著有《博奕论》一书,成为概率论的奠基者.在代数学上的一个重要贡献,是认真地引入了虚数,并接受虚数是方程式的根.
1873年,我国数学家华蘅芳将 “复数”引入中国!
情景导入
一般地,为了使方程=1有解,人们规定的平方等于=1,称为虚数单位。
所以方程 =-1的解为=或=-。
1.虚数的定义
例:解方程x =-2
解方程(x+1) =-2
说明:
(1)实数与i可以进行加法和乘法运算:
实数a与数i相加记为:a+i
实数b与数i相乘记为:bi ,并规定0 i =0
实数a与 bi相加记为:a+bi
(2)实数与 i 进行四则运算时,原有的加法、乘法运算律仍然成立.
z=a+bi(a,b∈R)
实部
虚部
虚数单位
形如a+bi(a,b∈R)的数,叫做复数,i为虚数单位.
所有复数组成的集合叫做复数集。通常用大写字母C表示。
2.复数的概念
实数集
虚数集
纯虚数集
复数集
记作:Re(z)=a,Im(z)=b.
说一说:指出下列复数的实部与虚部.
-1+2i , 2-3i, 2024 , i , 0 .
3.复数的分类
复数集C和实数集R之间有什么关系?
想一想
例1 分别求实数x的取值,使得复数z=(x-2)+(x+3)i
(1)是实数;(2)是虚数;(3)是纯虚数.
解:(1)当x+3=0,即x=-3时,复数z是实数.
(2)当x+3≠0,即x≠-3时,复数z是虚数.
(3)当x-2=0,且x+3≠0,即x=2时,复数z是纯虚数.
1.若a=0,则z=a+bi (a ∈ R、b ∈ R)为纯虚数.
2.若z=a+bi (a ∈ R、b ∈ R)为纯虚数,则a=0.
故a=0是z=a+bi (a ∈ R、b ∈ R)为纯虚数的
条件.
判一判
4.复数的相等
复数相等:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注:
2) 一般来说,两个复数只能说相等或不相等,而不能比较大小.
1)
例2 分别求满足下列关系式的实数与的值
(1);
(2)
解:(1)根据复数相等的定义,得
(2)根据复数等于0得充要条件,得
解这个方程组,得
解这个方程组,得
例3 已知关于x的方程x2+(1-2i)x+(3m-i)=0有实根,求实数m的值.
2.4-3a-a2i=a2+4ai,则实数a的值为( )
A.1 B.1或-4 C.-4 D.0或-4
C
1.若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为( )
A.1 B.2 C.1或2 D.-1
B
虚数的引入
复 数
复数的分类
复数的相等
z = a + bi
(a,b∈R)
当b=0时z为实数;
当b 0时z为虚数;
(此时,当a =0时z为纯虚数).
a=c
b=d
a+bi=c+di
(a,b,c,d R)
