2025年山东省济南市商河县七年级下学期数学期中考试试题(含答案)
文档属性
| 名称 | 2025年山东省济南市商河县七年级下学期数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 346.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 07:43:49 | ||
图片预览


文档简介
七年级下学期数学期中试题
本试卷分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分。本试题共 8 页,满分 150 分,考试时间为 120 分钟。
答卷前请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填在试卷规定的位置。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷 选择题(共 40 分)
一、选择题(本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列成语描述的事件为必然事件的是( )
A. 旭日东升 B. 空中楼阁 C. 水中捞月 D. 刻舟求剑
2.下列运算正确的是( )
A. a3+a3=a6 B. (a3)2=a6 C. (ab)2=ab2 D. 2a5·3a5=5a5
3.数学源于生活,寓于生活,用于生活.下列各选项中能用 “垂线段最短” 来解释的现象是( )
A. 测量跳远成绩 B. 木板上弹墨线
C. 弯曲河道改直 D. 两钉子固定木条
4.澳大利亚昆士兰大学的科学家在海底下约 4.8 公里深处的砂岩中,发现了一种世界上最小的神秘生物,它们的最大身长只有 0.00000015 米,甚至比已知的最小细菌还要小,将 0.00000015 用科学记数法表示为( )
A. 0.15×10 6 B. 1.5×10 7 C. 1.5×10 8 D. 15×10 9
5.下列各式中能用平方差公式计算的是( )
A. ( x+2y)(x 2y) B. (3x 5y)( 3x 5y) C. (1 5m)(5m 1) D. (a+b)(b+a)
6.如图,直线m∥n,一块含有30 的直角三角板按如图所示放置.若∠1=40 ,则∠2的大小为( )
A. 70 B. 60 C. 50 D. 40
7.如图,为某小组做 “用频率估计概率” 的实验时,绘制的频率分布折线图,则符合这一结果的实验是( )
A. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 抛两枚硬币,一枚正面朝上,一枚反面朝上
C. 掷一个正六面体的骰子,朝上点数是 3 的倍数
D. 一个装有 2 个红球 1 个黑球的袋子中任取一球,取到的是红球
8.如图,飞镖游戏板中的每一块小正方形都完全一样.假设飞镖击中任何一个位置都是等可能的,任意投掷飞镖 1 次,则飞镖击中白色区域的概率是( )
A. B. C. D.
9.如图,在△ABC中,∠BAC=90 ,AD,AE,BF分别是△ABC的高线、中线和角平分线,下列结论错误的是( )
A. ∠ABF=∠CBF B. ∠ABC=∠CAD C. S△ABE=S△ACE D. AF=CF
10.请看杨辉三角(如图),并观察下列等式:
根据前面各式的规律,则(a+b)40的第三项系数是( )
A. 730 B. 741 C. 780 D. 820
二、填空题(本大题共 6 小题,每小题 4 分,共 24 分)
11一个角的补角等于这个角的余角的,则这个角为______度.
12.小明做作业时,把一滴墨水滴在一道数学题上,题目变成了:,看不清x前面的数字是什么,只知道这是一个完全平方式,请你判断这个被墨水遮住的数字可能是 .
13.已知△ABC中,AB=8cm,AC=6cm,若在3cm、6cm、9cm、12cm、15cm五条线段中任选一条能作为BC边长的概率是 .
14.已知a2+a=3,则(2a 4)(a+3)的值是______.
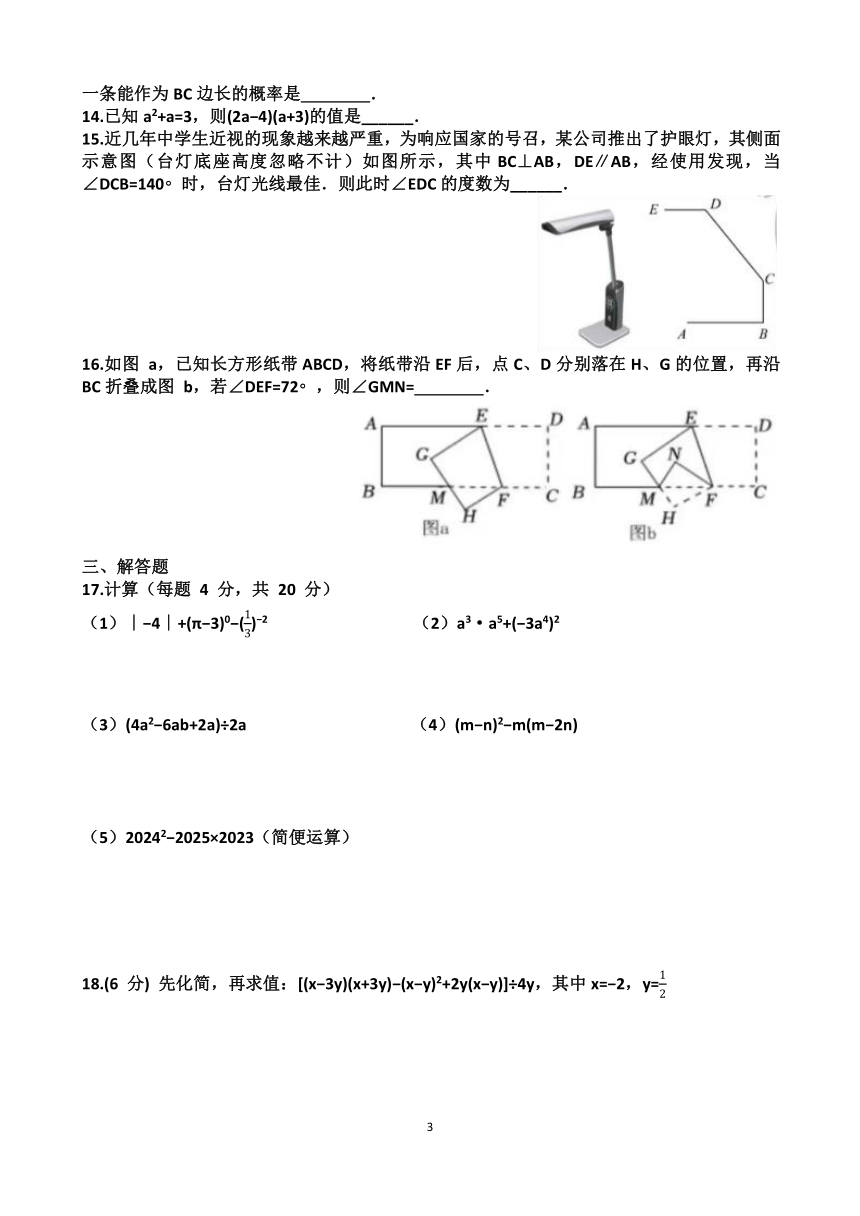
15.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了护眼灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中BC⊥AB,DE∥AB,经使用发现,当∠DCB=140 时,台灯光线最佳.则此时∠EDC的度数为______.
16.如图 a,已知长方形纸带ABCD,将纸带沿EF后,点C、D分别落在H、G的位置,再沿BC折叠成图 b,若∠DEF=72 ,则∠GMN= .
三、解答题
17.计算(每题 4 分,共 20 分)
(1)∣ 4∣+(π 3)0 () 2 (2)a3·a5+( 3a4)2
(3)(4a2 6ab+2a)÷2a (4)(m n)2 m(m 2n)
(5)20242 2025×2023(简便运算)
18.(6 分) 先化简,再求值:[(x 3y)(x+3y) (x y)2+2y(x y)]÷4y,其中x= 2,y=
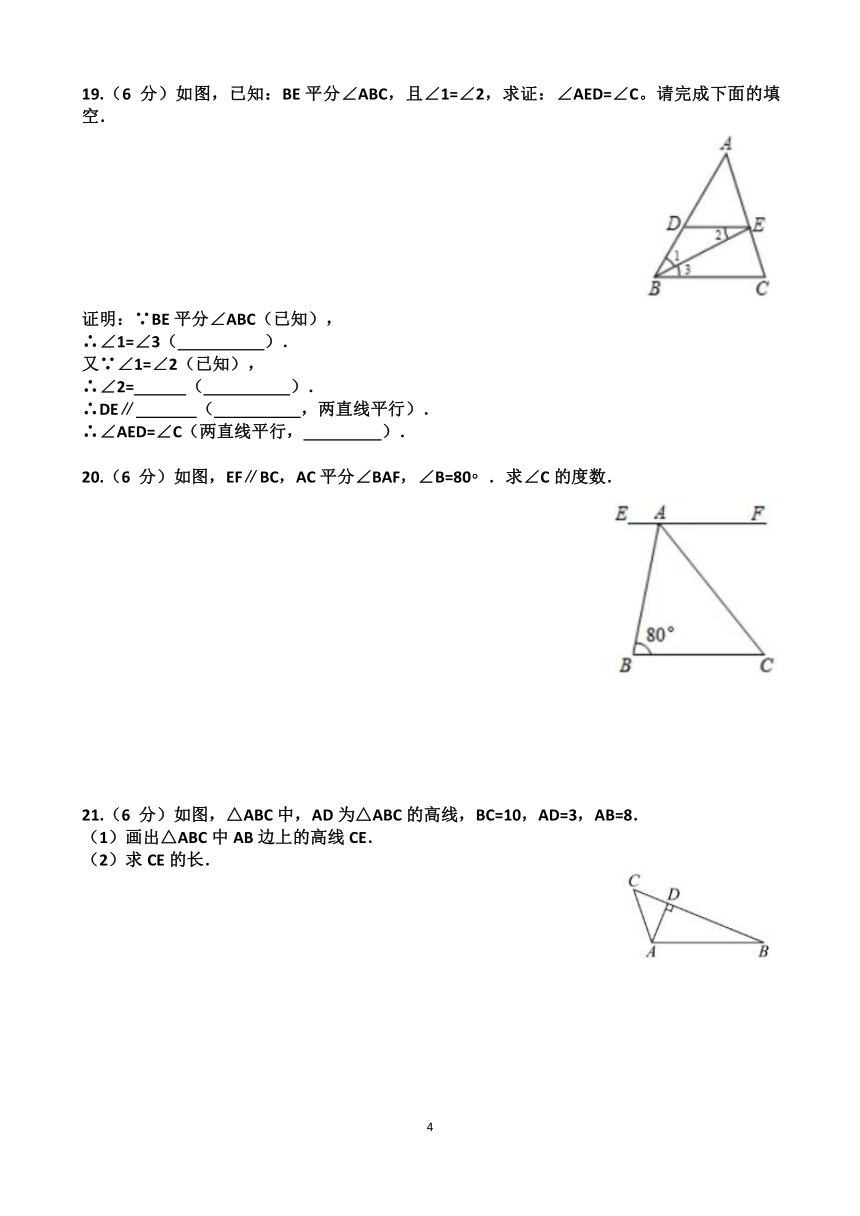
19.(6 分)如图,已知:BE平分∠ABC,且∠1=∠2,求证:∠AED=∠C。请完成下面的填空.
证明:∵BE平分∠ABC(已知),
∴∠1=∠3( ).
又∵∠1=∠2(已知),
∴∠2= ( ).
∴DE∥ ( ,两直线平行).
∴∠AED=∠C(两直线平行, ).
20.(6 分)如图,EF∥BC,AC平分∠BAF,∠B=80 .求∠C的度数.
21.(6 分)如图,△ABC中,AD为△ABC的高线,BC=10,AD=3,AB=8.
(1)画出△ABC中AB边上的高线CE.
(2)求CE的长.
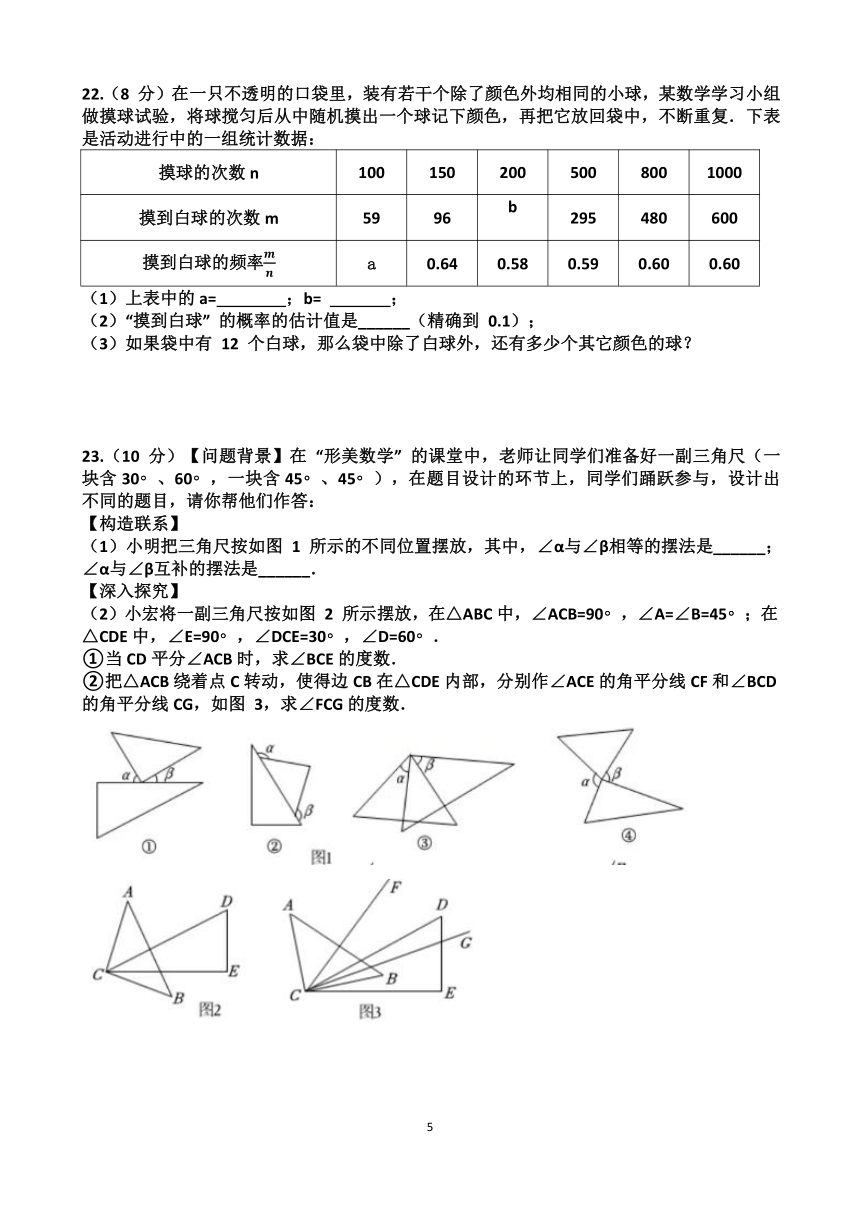
22.(8 分)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 600
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.60
(1)上表中的a= ;b= ;
(2)“摸到白球” 的概率的估计值是______(精确到 0.1);
(3)如果袋中有 12 个白球,那么袋中除了白球外,还有多少个其它颜色的球?
23.(10 分)【问题背景】在 “形美数学” 的课堂中,老师让同学们准备好一副三角尺(一块含30 、60 ,一块含45 、45 ),在题目设计的环节上,同学们踊跃参与,设计出不同的题目,请你帮他们作答:
【构造联系】
(1)小明把三角尺按如图 1 所示的不同位置摆放,其中,∠α与∠β相等的摆法是______;∠α与∠β互补的摆法是______.
【深入探究】
(2)小宏将一副三角尺按如图 2 所示摆放,在△ABC中,∠ACB=90 ,∠A=∠B=45 ;在
△CDE中,∠E=90 ,∠DCE=30 ,∠D=60 .
①当CD平分∠ACB时,求∠BCE的度数.
②把△ACB绕着点C转动,使得边CB在△CDE内部,分别作∠ACE的角平分线CF和∠BCD的角平分线CG,如图 3,求∠FCG的度数.
24.(12分)数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题。
【知识生成】
(1)请写出图 1,图 2,阴影部分的面积分别能解释的乘法公式。
图 1:________
图 2:________
【拓展探究】
(2)用 4 个全等的长和宽分别为 a,b 的长方形拼摆成一个如图 3 的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式(a+b)2,(a b)2,ab之间的等量关系是________。
【解决问题】
(3)如图 4,C 是线段 AB 上的一点,分别以 AC,BC 为边向两边作正方形 ACDE 和正方形 BCFG。已知AB=7,两正方形的面积和为 21,求△AFC的面积。
【知识迁移】
(4)当(2029 x)(x 2026)=时,则(2x 4055)2的值是________。(直接写出结果)
25.(12 分)【阅读探究】
如图 1,已知AB∥CD,E、F 分别是 AB、CD 上的点,点 M 在 AB、CD 两平行线之间,
∠AEM=45 ,∠CFM=25 ,求∠EMF的度数。
解:过点 M 作MN∥AB
∵AB∥CD
∴MN∥CD
∴∠EMN=∠AEM=45 ,∠FMN=∠CFM=25
∴∠EMF=∠EMN+∠FMN=45 +25 =70
从上面的推理过程中,我们发现平行线具有 “等角转化” 的功能,将∠AEM和∠CFM“凑” 在一起,得出角之间的关系,使问题得以解决。
【方法运用】
如图2,已知直线m∥n,AB 是一个平面镜,光线从直线 m 上的点 O 射出,在平面镜 AB 上经点 P 反射后,到达直线 n 上的点 Q。我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB。
(1)由图 2 写出∠AOP、∠BQP、∠OPQ之间的数量关系,并说明理由。
(2)如图 3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n 上,另一块在两直线之间四块平面镜构成四边形 ABCD 光线从点 O 以适当的角度射出后,其传播路径为
O→P→Q→R→O→P→
直接写出∠OPQ和∠ORQ的数量关系。
【应用拓展】
(3)问题情境:“公路村村通” 的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与外面的世界。数学活动课上,老师把山路抽象成图 4 所示的样子,并提出了一个问题:
在图 4 中,AB∥CD,∠B=125 ,∠PQC=65 ,∠C=145 ,求∠BPQ的度数。
答案
一、选择题(本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列成语描述的事件为必然事件的是( A )
A. 旭日东升 B. 空中楼阁 C. 水中捞月 D. 刻舟求剑
2.下列运算正确的是( B )
A. a3+a3=a6 B. (a3)2=a6 C. (ab)2=ab2 D. 2a5·3a5=5a5
3.数学源于生活,寓于生活,用于生活.下列各选项中能用 “垂线段最短” 来解释的现象是( A )
A. 测量跳远成绩 B. 木板上弹墨线
C. 弯曲河道改直 D. 两钉子固定木条
4.澳大利亚昆士兰大学的科学家在海底下约 4.8 公里深处的砂岩中,发现了一种世界上最小的神秘生物,它们的最大身长只有 0.00000015 米,甚至比已知的最小细菌还要小,将 0.00000015 用科学记数法表示为( B )
A. 0.15×10 6 B. 1.5×10 7 C. 1.5×10 8 D. 15×10 9
5.下列各式中能用平方差公式计算的是( B )
A. ( x+2y)(x 2y) B. (3x 5y)( 3x 5y) C. (1 5m)(5m 1) D. (a+b)(b+a)
6.如图,直线m∥n,一块含有30 的直角三角板按如图所示放置.若∠1=40 ,则∠2的大小为( A )
A. 70 B. 60 C. 50 D. 40
7.如图,为某小组做 “用频率估计概率” 的实验时,绘制的频率分布折线图,则符合这一结果的实验是( C )
A. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 抛两枚硬币,一枚正面朝上,一枚反面朝上
C. 掷一个正六面体的骰子,朝上点数是 3 的倍数
D. 一个装有 2 个红球 1 个黑球的袋子中任取一球,取到的是红球
8.如图,飞镖游戏板中的每一块小正方形都完全一样.假设飞镖击中任何一个位置都是等可能的,任意投掷飞镖 1 次,则飞镖击中白色区域的概率是( B )
A. B. C. D.
9.如图,在△ABC中,∠BAC=90 ,AD,AE,BF分别是△ABC的高线、中线和角平分线,下列结论错误的是( D )
A. ∠ABF=∠CBF B. ∠ABC=∠CAD C. S△ABE=S△ACE D. AF=CF
10.请看杨辉三角(如图),并观察下列等式:
根据前面各式的规律,则(a+b)40的第三项系数是( C )
A. 730 B. 741 C. 780 D. 820
二、填空题(本大题共 6 小题,每小题 4 分,共 24 分)
11一个角的补角等于这个角的余角的,则这个角为___18°___度.
12.小明做作业时,把一滴墨水滴在一道数学题上,题目变成了:,看不清x前面的数字是什么,只知道这是一个完全平方式,请你判断这个被墨水遮住的数字可能是 ±8 .
13.已知△ABC中,AB=8cm,AC=6cm,若在3cm、6cm、9cm、12cm、15cm五条线段中任选一条能作为BC边长的概率是 .
14.已知a2+a=3,则(2a 4)(a+3)的值是___﹣6___.
15.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了护眼灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中BC⊥AB,DE∥AB,经使用发现,当∠DCB=140 时,台灯光线最佳.则此时∠EDC的度数为___130°___.
16.如图 a,已知长方形纸带ABCD,将纸带沿EF后,点C、D分别落在H、G的位置,再沿BC折叠成图 b,若∠DEF=72 ,则∠GMN= 72° .
三、解答题
17.计算(每题 4 分,共 20 分)
(1)∣ 4∣+(π 3)0 () 2 (2)a3·a5+( 3a4)2
=4+1﹣9 =a8+9a8
=﹣4 =10a8
(3)(4a2 6ab+2a)÷2a (4)(m n)2 m(m 2n)
=2a﹣3b+1 =m2﹣2mn+n2﹣m2+2mn
=n2
(5)20242 2025×2023(简便运算)
=20242 (2024+1)×(2024﹣1)
=1
18.(6 分) 先化简,再求值:[(x 3y)(x+3y) (x y)2+2y(x y)]÷4y,其中x= 2,y=
解:原式=[x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2]÷4y
=﹣3y+x
将x= 2,y=代入得﹣
19.(6 分)如图,已知:BE平分∠ABC,且∠1=∠2,求证:∠AED=∠C。请完成下面的填空.
证明:∵BE平分∠ABC(已知),
∴∠1=∠3( 角平分线定义 ).
又∵∠1=∠2(已知),
∴∠2= ∠3 ( 等量代换 ).
∴DE∥ BC ( 内错角相等 ,两直线平行).
∴∠AED=∠C(两直线平行, 同位角相等 ).
20.(6 分)如图,EF∥BC,AC平分∠BAF,∠B=80 .求∠C的度数.
解:∵EF // BC ,∠B =80(已知)
∴∠BAF =180°-∠B =100(两直线平行,同旁内角互补)
∠C = ∠CAF (两直线平行,内错角相等)
又:AC 平分∠BAF (已知)
∴∠CAF=∠BAF =50°(角平分线的定义)
∴∠C =∠CAF =50°(等量代换)
21.(6 分)如图,△ABC中,AD为△ABC的高线,BC=10,AD=3,AB=8.
(1)画出△ABC中AB边上的高线CE.
(2)求CE的长.
(1)解:如图所示,CE 即为所求;
(2)解:∵AD 为△ ABC 的高线, BC =10, AD =3, AB =8,
∴△ABC的面积=BC·AD =AB·CE
×10×3=×8CE.
∴CE =
22.(8 分)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 600
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.60
(1)上表中的a= ;b= ;
(2)“摸到白球” 的概率的估计值是______(精确到 0.1);
(3)如果袋中有 12 个白球,那么袋中除了白球外,还有多少个其它颜色的球?
(1)0.59,116(2)0.6
(3)12÷0.6=20(个),20-12=8(个)
答:还有8个其它颜色的球
23.(10 分)【问题背景】在 “形美数学” 的课堂中,老师让同学们准备好一副三角尺(一块含30 、60 ,一块含45 、45 ),在题目设计的环节上,同学们踊跃参与,设计出不同的题目,请你帮他们作答:
【构造联系】
(1)小明把三角尺按如图 1 所示的不同位置摆放,其中,∠α与∠β相等的摆法是______;∠α与∠β互补的摆法是______.
【深入探究】
(2)小宏将一副三角尺按如图 2 所示摆放,在△ABC中,∠ACB=90 ,∠A=∠B=45 ;在
△CDE中,∠E=90 ,∠DCE=30 ,∠D=60 .
①当CD平分∠ACB时,求∠BCE的度数.
②把△ACB绕着点C转动,使得边CB在△CDE内部,分别作∠ACE的角平分线CF和∠BCD的角平分线CG,如图 3,求∠FCG的度数.
(1)②③④
(2)①∵CD 平分∠ACB
∴∠BCD =∠ACB=4S°
∴∠BCE=45°-30°=15°:
②∵CF平分∠ACE
∴∠BCD=∠ACB =45°
∵CG 平分∠BCD
∴∠BCG =∠BCD =(∠DCE-∠BCE )=(30°-∠BCE ).
∴∠FCG =∠ECF -∠ECG =45°+∠BCE -∠BCE -∠BCG =45°-∠BCE -(15°-∠BCE )=45°-∠BCE-15+-∠BCE=30°
24.(12分)数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题。
【知识生成】
(1)请写出图 1,图 2,阴影部分的面积分别能解释的乘法公式。
图 1:________
图 2:________
【拓展探究】
(2)用 4 个全等的长和宽分别为 a,b 的长方形拼摆成一个如图 3 的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式(a+b)2,(a b)2,ab之间的等量关系是________。
【解决问题】
(3)如图 4,C 是线段 AB 上的一点,分别以 AC,BC 为边向两边作正方形 ACDE 和正方形 BCFG。已知AB=7,两正方形的面积和为 21,求△AFC的面积。
【知识迁移】
(4)当(2029 x)(x 2026)=时,则(2x 4055)2的值是________。(直接写出结果)
(1)(a+b)2(a-b)2
(2)( a+ b)2-(a - b)=4ab
(3)由题意可知 AC + BC =7, S正方形ACDE + S正方形BCFG =21,
∴AC2+BC2=21
∴( AC+ BC)2-(AC2+BC2)=72-21
∴AC·BC =14,
∴S△MCP =7
25.(12 分)【阅读探究】
如图 1,已知AB∥CD,E、F 分别是 AB、CD 上的点,点 M 在 AB、CD 两平行线之间,
∠AEM=45 ,∠CFM=25 ,求∠EMF的度数。
解:过点 M 作MN∥AB
∵AB∥CD
∴MN∥CD
∴∠EMN=∠AEM=45 ,∠FMN=∠CFM=25
∴∠EMF=∠EMN+∠FMN=45 +25 =70
从上面的推理过程中,我们发现平行线具有 “等角转化” 的功能,将∠AEM和∠CFM“凑” 在一起,得出角之间的关系,使问题得以解决。
【方法运用】
如图2,已知直线m∥n,AB 是一个平面镜,光线从直线 m 上的点 O 射出,在平面镜 AB 上经点 P 反射后,到达直线 n 上的点 Q。我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB。
(1)由图 2 写出∠AOP、∠BQP、∠OPQ之间的数量关系,并说明理由。
(2)如图 3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n 上,另一块在两直线之间四块平面镜构成四边形 ABCD 光线从点 O 以适当的角度射出后,其传播路径为
O→P→Q→R→O→P→
直接写出∠OPQ和∠ORQ的数量关系。
【应用拓展】
(3)问题情境:“公路村村通” 的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与外面的世界。数学活动课上,老师把山路抽象成图 4 所示的样子,并提出了一个问题:
在图 4 中,AB∥CD,∠B=125 ,∠PQC=65 ,∠C=145 ,求∠BPQ的度数。
(1) ∠OPQ =∠AOP +∠BQP ,
理由如下,如图所示,过点P 作 PE // OA ,则PE //BQ .
∴∠AOP =∠OPE , ∠BQP =∠QPE .
∴∠OPQ =∠OPE +∠QPE
∴∠OPQ=∠AOP +∠BQP :
(2)∠OPQ=∠ORQ
【应用拓展】如图,过点 P 作 PM // AB。过点 Q作QN //AB
则AB //PM // QN//CD .
∴∠ABP +∠BPM =180,∠MPQ =∠PQN , ∠DCQ +∠CQN =180
∵∠B=125°,∠C=145°
∴∠BPM =180°-125°=55°,∠CQN =180°-145°=35°
∵∠PQC -65°
∴∠PQN =∠PQC -∠CQN -65°-35°=30°
∴∠QPM=∠PQN =30°,
∴∠BPQ -∠BPM +∠QPM =30°+55°=85°.
本试卷分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分。本试题共 8 页,满分 150 分,考试时间为 120 分钟。
答卷前请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填在试卷规定的位置。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷 选择题(共 40 分)
一、选择题(本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列成语描述的事件为必然事件的是( )
A. 旭日东升 B. 空中楼阁 C. 水中捞月 D. 刻舟求剑
2.下列运算正确的是( )
A. a3+a3=a6 B. (a3)2=a6 C. (ab)2=ab2 D. 2a5·3a5=5a5
3.数学源于生活,寓于生活,用于生活.下列各选项中能用 “垂线段最短” 来解释的现象是( )
A. 测量跳远成绩 B. 木板上弹墨线
C. 弯曲河道改直 D. 两钉子固定木条
4.澳大利亚昆士兰大学的科学家在海底下约 4.8 公里深处的砂岩中,发现了一种世界上最小的神秘生物,它们的最大身长只有 0.00000015 米,甚至比已知的最小细菌还要小,将 0.00000015 用科学记数法表示为( )
A. 0.15×10 6 B. 1.5×10 7 C. 1.5×10 8 D. 15×10 9
5.下列各式中能用平方差公式计算的是( )
A. ( x+2y)(x 2y) B. (3x 5y)( 3x 5y) C. (1 5m)(5m 1) D. (a+b)(b+a)
6.如图,直线m∥n,一块含有30 的直角三角板按如图所示放置.若∠1=40 ,则∠2的大小为( )
A. 70 B. 60 C. 50 D. 40
7.如图,为某小组做 “用频率估计概率” 的实验时,绘制的频率分布折线图,则符合这一结果的实验是( )
A. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 抛两枚硬币,一枚正面朝上,一枚反面朝上
C. 掷一个正六面体的骰子,朝上点数是 3 的倍数
D. 一个装有 2 个红球 1 个黑球的袋子中任取一球,取到的是红球
8.如图,飞镖游戏板中的每一块小正方形都完全一样.假设飞镖击中任何一个位置都是等可能的,任意投掷飞镖 1 次,则飞镖击中白色区域的概率是( )
A. B. C. D.
9.如图,在△ABC中,∠BAC=90 ,AD,AE,BF分别是△ABC的高线、中线和角平分线,下列结论错误的是( )
A. ∠ABF=∠CBF B. ∠ABC=∠CAD C. S△ABE=S△ACE D. AF=CF
10.请看杨辉三角(如图),并观察下列等式:
根据前面各式的规律,则(a+b)40的第三项系数是( )
A. 730 B. 741 C. 780 D. 820
二、填空题(本大题共 6 小题,每小题 4 分,共 24 分)
11一个角的补角等于这个角的余角的,则这个角为______度.
12.小明做作业时,把一滴墨水滴在一道数学题上,题目变成了:,看不清x前面的数字是什么,只知道这是一个完全平方式,请你判断这个被墨水遮住的数字可能是 .
13.已知△ABC中,AB=8cm,AC=6cm,若在3cm、6cm、9cm、12cm、15cm五条线段中任选一条能作为BC边长的概率是 .
14.已知a2+a=3,则(2a 4)(a+3)的值是______.
15.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了护眼灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中BC⊥AB,DE∥AB,经使用发现,当∠DCB=140 时,台灯光线最佳.则此时∠EDC的度数为______.
16.如图 a,已知长方形纸带ABCD,将纸带沿EF后,点C、D分别落在H、G的位置,再沿BC折叠成图 b,若∠DEF=72 ,则∠GMN= .
三、解答题
17.计算(每题 4 分,共 20 分)
(1)∣ 4∣+(π 3)0 () 2 (2)a3·a5+( 3a4)2
(3)(4a2 6ab+2a)÷2a (4)(m n)2 m(m 2n)
(5)20242 2025×2023(简便运算)
18.(6 分) 先化简,再求值:[(x 3y)(x+3y) (x y)2+2y(x y)]÷4y,其中x= 2,y=
19.(6 分)如图,已知:BE平分∠ABC,且∠1=∠2,求证:∠AED=∠C。请完成下面的填空.
证明:∵BE平分∠ABC(已知),
∴∠1=∠3( ).
又∵∠1=∠2(已知),
∴∠2= ( ).
∴DE∥ ( ,两直线平行).
∴∠AED=∠C(两直线平行, ).
20.(6 分)如图,EF∥BC,AC平分∠BAF,∠B=80 .求∠C的度数.
21.(6 分)如图,△ABC中,AD为△ABC的高线,BC=10,AD=3,AB=8.
(1)画出△ABC中AB边上的高线CE.
(2)求CE的长.
22.(8 分)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 600
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.60
(1)上表中的a= ;b= ;
(2)“摸到白球” 的概率的估计值是______(精确到 0.1);
(3)如果袋中有 12 个白球,那么袋中除了白球外,还有多少个其它颜色的球?
23.(10 分)【问题背景】在 “形美数学” 的课堂中,老师让同学们准备好一副三角尺(一块含30 、60 ,一块含45 、45 ),在题目设计的环节上,同学们踊跃参与,设计出不同的题目,请你帮他们作答:
【构造联系】
(1)小明把三角尺按如图 1 所示的不同位置摆放,其中,∠α与∠β相等的摆法是______;∠α与∠β互补的摆法是______.
【深入探究】
(2)小宏将一副三角尺按如图 2 所示摆放,在△ABC中,∠ACB=90 ,∠A=∠B=45 ;在
△CDE中,∠E=90 ,∠DCE=30 ,∠D=60 .
①当CD平分∠ACB时,求∠BCE的度数.
②把△ACB绕着点C转动,使得边CB在△CDE内部,分别作∠ACE的角平分线CF和∠BCD的角平分线CG,如图 3,求∠FCG的度数.
24.(12分)数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题。
【知识生成】
(1)请写出图 1,图 2,阴影部分的面积分别能解释的乘法公式。
图 1:________
图 2:________
【拓展探究】
(2)用 4 个全等的长和宽分别为 a,b 的长方形拼摆成一个如图 3 的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式(a+b)2,(a b)2,ab之间的等量关系是________。
【解决问题】
(3)如图 4,C 是线段 AB 上的一点,分别以 AC,BC 为边向两边作正方形 ACDE 和正方形 BCFG。已知AB=7,两正方形的面积和为 21,求△AFC的面积。
【知识迁移】
(4)当(2029 x)(x 2026)=时,则(2x 4055)2的值是________。(直接写出结果)
25.(12 分)【阅读探究】
如图 1,已知AB∥CD,E、F 分别是 AB、CD 上的点,点 M 在 AB、CD 两平行线之间,
∠AEM=45 ,∠CFM=25 ,求∠EMF的度数。
解:过点 M 作MN∥AB
∵AB∥CD
∴MN∥CD
∴∠EMN=∠AEM=45 ,∠FMN=∠CFM=25
∴∠EMF=∠EMN+∠FMN=45 +25 =70
从上面的推理过程中,我们发现平行线具有 “等角转化” 的功能,将∠AEM和∠CFM“凑” 在一起,得出角之间的关系,使问题得以解决。
【方法运用】
如图2,已知直线m∥n,AB 是一个平面镜,光线从直线 m 上的点 O 射出,在平面镜 AB 上经点 P 反射后,到达直线 n 上的点 Q。我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB。
(1)由图 2 写出∠AOP、∠BQP、∠OPQ之间的数量关系,并说明理由。
(2)如图 3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n 上,另一块在两直线之间四块平面镜构成四边形 ABCD 光线从点 O 以适当的角度射出后,其传播路径为
O→P→Q→R→O→P→
直接写出∠OPQ和∠ORQ的数量关系。
【应用拓展】
(3)问题情境:“公路村村通” 的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与外面的世界。数学活动课上,老师把山路抽象成图 4 所示的样子,并提出了一个问题:
在图 4 中,AB∥CD,∠B=125 ,∠PQC=65 ,∠C=145 ,求∠BPQ的度数。
答案
一、选择题(本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列成语描述的事件为必然事件的是( A )
A. 旭日东升 B. 空中楼阁 C. 水中捞月 D. 刻舟求剑
2.下列运算正确的是( B )
A. a3+a3=a6 B. (a3)2=a6 C. (ab)2=ab2 D. 2a5·3a5=5a5
3.数学源于生活,寓于生活,用于生活.下列各选项中能用 “垂线段最短” 来解释的现象是( A )
A. 测量跳远成绩 B. 木板上弹墨线
C. 弯曲河道改直 D. 两钉子固定木条
4.澳大利亚昆士兰大学的科学家在海底下约 4.8 公里深处的砂岩中,发现了一种世界上最小的神秘生物,它们的最大身长只有 0.00000015 米,甚至比已知的最小细菌还要小,将 0.00000015 用科学记数法表示为( B )
A. 0.15×10 6 B. 1.5×10 7 C. 1.5×10 8 D. 15×10 9
5.下列各式中能用平方差公式计算的是( B )
A. ( x+2y)(x 2y) B. (3x 5y)( 3x 5y) C. (1 5m)(5m 1) D. (a+b)(b+a)
6.如图,直线m∥n,一块含有30 的直角三角板按如图所示放置.若∠1=40 ,则∠2的大小为( A )
A. 70 B. 60 C. 50 D. 40
7.如图,为某小组做 “用频率估计概率” 的实验时,绘制的频率分布折线图,则符合这一结果的实验是( C )
A. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 抛两枚硬币,一枚正面朝上,一枚反面朝上
C. 掷一个正六面体的骰子,朝上点数是 3 的倍数
D. 一个装有 2 个红球 1 个黑球的袋子中任取一球,取到的是红球
8.如图,飞镖游戏板中的每一块小正方形都完全一样.假设飞镖击中任何一个位置都是等可能的,任意投掷飞镖 1 次,则飞镖击中白色区域的概率是( B )
A. B. C. D.
9.如图,在△ABC中,∠BAC=90 ,AD,AE,BF分别是△ABC的高线、中线和角平分线,下列结论错误的是( D )
A. ∠ABF=∠CBF B. ∠ABC=∠CAD C. S△ABE=S△ACE D. AF=CF
10.请看杨辉三角(如图),并观察下列等式:
根据前面各式的规律,则(a+b)40的第三项系数是( C )
A. 730 B. 741 C. 780 D. 820
二、填空题(本大题共 6 小题,每小题 4 分,共 24 分)
11一个角的补角等于这个角的余角的,则这个角为___18°___度.
12.小明做作业时,把一滴墨水滴在一道数学题上,题目变成了:,看不清x前面的数字是什么,只知道这是一个完全平方式,请你判断这个被墨水遮住的数字可能是 ±8 .
13.已知△ABC中,AB=8cm,AC=6cm,若在3cm、6cm、9cm、12cm、15cm五条线段中任选一条能作为BC边长的概率是 .
14.已知a2+a=3,则(2a 4)(a+3)的值是___﹣6___.
15.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了护眼灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中BC⊥AB,DE∥AB,经使用发现,当∠DCB=140 时,台灯光线最佳.则此时∠EDC的度数为___130°___.
16.如图 a,已知长方形纸带ABCD,将纸带沿EF后,点C、D分别落在H、G的位置,再沿BC折叠成图 b,若∠DEF=72 ,则∠GMN= 72° .
三、解答题
17.计算(每题 4 分,共 20 分)
(1)∣ 4∣+(π 3)0 () 2 (2)a3·a5+( 3a4)2
=4+1﹣9 =a8+9a8
=﹣4 =10a8
(3)(4a2 6ab+2a)÷2a (4)(m n)2 m(m 2n)
=2a﹣3b+1 =m2﹣2mn+n2﹣m2+2mn
=n2
(5)20242 2025×2023(简便运算)
=20242 (2024+1)×(2024﹣1)
=1
18.(6 分) 先化简,再求值:[(x 3y)(x+3y) (x y)2+2y(x y)]÷4y,其中x= 2,y=
解:原式=[x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2]÷4y
=﹣3y+x
将x= 2,y=代入得﹣
19.(6 分)如图,已知:BE平分∠ABC,且∠1=∠2,求证:∠AED=∠C。请完成下面的填空.
证明:∵BE平分∠ABC(已知),
∴∠1=∠3( 角平分线定义 ).
又∵∠1=∠2(已知),
∴∠2= ∠3 ( 等量代换 ).
∴DE∥ BC ( 内错角相等 ,两直线平行).
∴∠AED=∠C(两直线平行, 同位角相等 ).
20.(6 分)如图,EF∥BC,AC平分∠BAF,∠B=80 .求∠C的度数.
解:∵EF // BC ,∠B =80(已知)
∴∠BAF =180°-∠B =100(两直线平行,同旁内角互补)
∠C = ∠CAF (两直线平行,内错角相等)
又:AC 平分∠BAF (已知)
∴∠CAF=∠BAF =50°(角平分线的定义)
∴∠C =∠CAF =50°(等量代换)
21.(6 分)如图,△ABC中,AD为△ABC的高线,BC=10,AD=3,AB=8.
(1)画出△ABC中AB边上的高线CE.
(2)求CE的长.
(1)解:如图所示,CE 即为所求;
(2)解:∵AD 为△ ABC 的高线, BC =10, AD =3, AB =8,
∴△ABC的面积=BC·AD =AB·CE
×10×3=×8CE.
∴CE =
22.(8 分)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 600
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.60
(1)上表中的a= ;b= ;
(2)“摸到白球” 的概率的估计值是______(精确到 0.1);
(3)如果袋中有 12 个白球,那么袋中除了白球外,还有多少个其它颜色的球?
(1)0.59,116(2)0.6
(3)12÷0.6=20(个),20-12=8(个)
答:还有8个其它颜色的球
23.(10 分)【问题背景】在 “形美数学” 的课堂中,老师让同学们准备好一副三角尺(一块含30 、60 ,一块含45 、45 ),在题目设计的环节上,同学们踊跃参与,设计出不同的题目,请你帮他们作答:
【构造联系】
(1)小明把三角尺按如图 1 所示的不同位置摆放,其中,∠α与∠β相等的摆法是______;∠α与∠β互补的摆法是______.
【深入探究】
(2)小宏将一副三角尺按如图 2 所示摆放,在△ABC中,∠ACB=90 ,∠A=∠B=45 ;在
△CDE中,∠E=90 ,∠DCE=30 ,∠D=60 .
①当CD平分∠ACB时,求∠BCE的度数.
②把△ACB绕着点C转动,使得边CB在△CDE内部,分别作∠ACE的角平分线CF和∠BCD的角平分线CG,如图 3,求∠FCG的度数.
(1)②③④
(2)①∵CD 平分∠ACB
∴∠BCD =∠ACB=4S°
∴∠BCE=45°-30°=15°:
②∵CF平分∠ACE
∴∠BCD=∠ACB =45°
∵CG 平分∠BCD
∴∠BCG =∠BCD =(∠DCE-∠BCE )=(30°-∠BCE ).
∴∠FCG =∠ECF -∠ECG =45°+∠BCE -∠BCE -∠BCG =45°-∠BCE -(15°-∠BCE )=45°-∠BCE-15+-∠BCE=30°
24.(12分)数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题。
【知识生成】
(1)请写出图 1,图 2,阴影部分的面积分别能解释的乘法公式。
图 1:________
图 2:________
【拓展探究】
(2)用 4 个全等的长和宽分别为 a,b 的长方形拼摆成一个如图 3 的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式(a+b)2,(a b)2,ab之间的等量关系是________。
【解决问题】
(3)如图 4,C 是线段 AB 上的一点,分别以 AC,BC 为边向两边作正方形 ACDE 和正方形 BCFG。已知AB=7,两正方形的面积和为 21,求△AFC的面积。
【知识迁移】
(4)当(2029 x)(x 2026)=时,则(2x 4055)2的值是________。(直接写出结果)
(1)(a+b)2(a-b)2
(2)( a+ b)2-(a - b)=4ab
(3)由题意可知 AC + BC =7, S正方形ACDE + S正方形BCFG =21,
∴AC2+BC2=21
∴( AC+ BC)2-(AC2+BC2)=72-21
∴AC·BC =14,
∴S△MCP =7
25.(12 分)【阅读探究】
如图 1,已知AB∥CD,E、F 分别是 AB、CD 上的点,点 M 在 AB、CD 两平行线之间,
∠AEM=45 ,∠CFM=25 ,求∠EMF的度数。
解:过点 M 作MN∥AB
∵AB∥CD
∴MN∥CD
∴∠EMN=∠AEM=45 ,∠FMN=∠CFM=25
∴∠EMF=∠EMN+∠FMN=45 +25 =70
从上面的推理过程中,我们发现平行线具有 “等角转化” 的功能,将∠AEM和∠CFM“凑” 在一起,得出角之间的关系,使问题得以解决。
【方法运用】
如图2,已知直线m∥n,AB 是一个平面镜,光线从直线 m 上的点 O 射出,在平面镜 AB 上经点 P 反射后,到达直线 n 上的点 Q。我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB。
(1)由图 2 写出∠AOP、∠BQP、∠OPQ之间的数量关系,并说明理由。
(2)如图 3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n 上,另一块在两直线之间四块平面镜构成四边形 ABCD 光线从点 O 以适当的角度射出后,其传播路径为
O→P→Q→R→O→P→
直接写出∠OPQ和∠ORQ的数量关系。
【应用拓展】
(3)问题情境:“公路村村通” 的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与外面的世界。数学活动课上,老师把山路抽象成图 4 所示的样子,并提出了一个问题:
在图 4 中,AB∥CD,∠B=125 ,∠PQC=65 ,∠C=145 ,求∠BPQ的度数。
(1) ∠OPQ =∠AOP +∠BQP ,
理由如下,如图所示,过点P 作 PE // OA ,则PE //BQ .
∴∠AOP =∠OPE , ∠BQP =∠QPE .
∴∠OPQ =∠OPE +∠QPE
∴∠OPQ=∠AOP +∠BQP :
(2)∠OPQ=∠ORQ
【应用拓展】如图,过点 P 作 PM // AB。过点 Q作QN //AB
则AB //PM // QN//CD .
∴∠ABP +∠BPM =180,∠MPQ =∠PQN , ∠DCQ +∠CQN =180
∵∠B=125°,∠C=145°
∴∠BPM =180°-125°=55°,∠CQN =180°-145°=35°
∵∠PQC -65°
∴∠PQN =∠PQC -∠CQN -65°-35°=30°
∴∠QPM=∠PQN =30°,
∴∠BPQ -∠BPM +∠QPM =30°+55°=85°.
同课章节目录
