人教版物理高三选修3-5第十六章第五节反冲运动 火箭同步训练
文档属性
| 名称 | 人教版物理高三选修3-5第十六章第五节反冲运动 火箭同步训练 |
|
|
| 格式 | doc | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-06-03 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
人教版物理高三选修3-5第十六章
第五节反冲运动 火箭同步训练
一.选择题
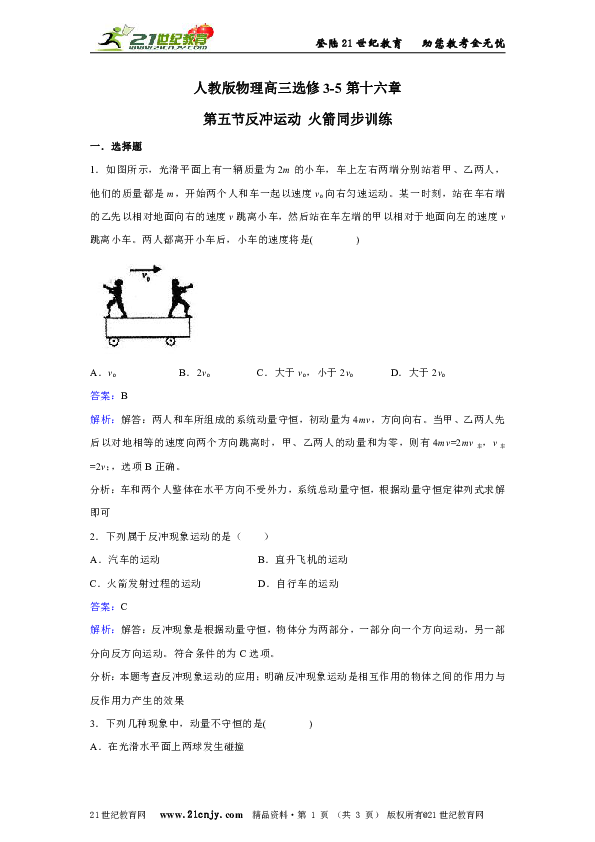
1.如图所示,光滑平面上有一辆质量为2m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度vo向右匀速运动。某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车。两人都离开小车后,小车的速度将是( )
A.vo B.2vo C.大于vo,小于2vo D.大于2vo
答案:B
解析:解答:两人和车所组成的系统动量守恒,初动量为4mv,方向向右。当甲、乙两人先后以对地相等的速度向两个方向跳离时,甲、乙两人的动量和为零,则有4mv=2mv车,v车=2v;,选项B正确。
分析:车和两个人整体在水平方向不受外力,系统总动量守恒,根据动量守恒定律列式求解即可
2.下列属于反冲现象运动的是( )
A.汽车的运动 B.直升飞机的运动
C.火箭发射过程的运动 D.自行车的运动
答案:C
解析:解答:反冲现象是根据动量守恒,物体分为两部分,一部分向一个方向运动,另一部分向反方向运动。符合条件的为C选项。
分析:本题考查反冲现象运动的应用;明确反冲现象运动是相互作用的物体之间的作用力与反作用力产生的效果
3.下列几种现象中,动量不守恒的是( )
A.在光滑水平面上两球发生碰撞
B.车原来静止在光滑的水平面上,车上的人从车头走到车尾
C.水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动
D.火箭的反冲现象运动
答案:C
解析:解答:在光滑水平面上两球发生碰撞,系统所受合外力为零,故动量守恒车原来静止在光滑的水平面上,车上的人从车头走到车尾,系统所受合外力为零,故动量守恒
水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动,系统所受合外力不为零,故动量不守恒火箭的反冲现象运动,系统内力远大于外力,故动量守恒选动量不守恒的情况,所以选C
分析:动量守恒的条件是:系统所受合外力为零,或者系统内力远大于外力情况
4.在光滑水平面上有两辆车,上面分别站着A、B两个人,人与车的质量总和相等,在A的手中拿有一个球,两车均保持静止状态.当A将手中球抛给B,B接到后,又抛给A,如此反复多次,最后球落在B的手中.则关于A、B速率的大小是( )
A.A、B两车速率相等
B.A车速率大
C.A车速率小
D.两车均保持静止状态
答案:B
解析:解答:由动量守恒可知,总动量始终为零,则两辆车(包括各自车上站的人)的动量大小相等,方向相反.这样质量大的速度就小,最后球在B车上,所以A车速度大.?
分析:以整体为研究对象,水平方向动量守恒,依据动量守恒列方程即可判断二者速度的大小
5.如图所示,一个质量为m的玩具蛙蹲在质量为m′的小车的细杆上,小车放在光滑的水平桌面上.若车长为,细杆高为h,且位于小车的中点,则玩具蛙至少以多大的水平速度v0跳出时,才能落到桌面上( )
A.v B.3 C.2 D.
答案:D
解析:解答:设蛙水平跳出速度为v0,小车后退速度为v1,则与蛙在车作用过程中,系统水平方向动量守恒,则
0=mv0-m′v1(以v0方向为正).
在蛙未落至桌面前,小车以v1做匀速运动,设t内走x,则
x=v1·t(x为对地位移).
在t时间内,蛙做平抛运动,根据平抛运动规律,即
,蛙对地的水平位移应为,而至少应为.
解以上各式得.
分析:车与蛙系统动量守恒,蛙跳出后做平抛运动,应用动量守恒定律与平抛运动规律求出速度
6.一个人在地面上立定跳远最好成绩是s.假设他站在静止于地面的小车的A端(车与地面的摩擦不计),如图所示,他欲从A端跳上L远处的站台上,则……( )
A.只要LB.只要LC.只要L=s,他一定能跳上站台
D.只要L=s,他有可能跳上站台
答案:B
解析:解答:由于反冲现象作用,运动员从车上起跳的最好成绩一定小于s,故选项B正确.
分析:当人往站台上跳的时候,人有一个向站台的速度,由于动量守恒,车子必然有一个离开站台的速度.
这样的话,如果L=S或L>S,人就一定跳不到站台上了,L<S,人才有可能跳上站台
7.人静止于光滑冰面上,现欲前进,下列方法中可行的是( )
A.向后踢腿
B.手臂向前甩
C.在冰上滚
D.脱去外衣向后投掷
答案:D
解析:解答:欲使物体获得一定的动量,必须有外力作用在该物体上.A、B两种方法属于物体两部分间的作用,不会对物体产生冲量;因冰面是光滑的,故C也不行.
分析:选取合适的系统为研究对象,根据动量守恒定律进行分析
8.假设一小型火箭沿人造地球卫星的轨道在高空中做匀速圆周运动.如果火箭向跟其速度相反的方向射出一个质量不可忽略的物体A,则下列情况哪些是能够成立的( )
A.物体A可能竖直落下地球,火箭可能沿原轨道运动
B.A跟火箭都不可能沿原轨道运动
C.A运行轨道半径将减小,火箭运动轨道半径将减小
D.A可能沿地球半径方向竖直下落,火箭运行的轨道半径增大
答案:D
解析:解答:火箭绕地球做匀速圆周运动时,万有引力刚好充当向心力,在轨迹切线方向无外力作用,故火箭沿切线向后发射物体过程中,系统沿轨道切线方向动量守恒,所以v′>v0.所以火箭要做离心运动,即火箭不可能在原轨道上运行.至于被发射的物体A,由于发射时做功情况的不同,发射后的A,速度可沿原运动方向,但速度变小,要做向心运动,即轨道半径变小;速度也可能刚好为零(对地),以后则竖直下落;速度也可能大小刚好等于火箭原飞行速度,所以A也可能在原轨道上运行,只是绕行方向与火箭绕行方向相反.综上讨论可知,正确选项为D.
分析:整个过程中系统动量守恒,而抛出后A的速度方向有几种可能,根据抛出后A的速度的大小和方向结合向心力的知识判断A物体的运动情况
9.一人静止于光滑的水平冰面上,现欲离开冰面,下列方法中可行的是( )
A.向后踢腿 B.手臂向后甩 C.在冰面上滚动 D.脱下外衣水平抛出
答案:D
解析:解答:把人和外衣看作系统,由动量守恒定律可知:衣服向后抛出时,人会向前反冲现象,故D对.由于人体各部分总动量为零,故A、B皆错.由于冰面“光滑”,故人不可能在冰面上滚动,D错.
分析:选取合适的系统为研究对象,根据动量守恒定律进行分析
10.在光滑水平面上停放着一辆平板车,车上站着质量分别为m1和m2的两个人.现两人都以相同的对地速度,从车尾跳下车.如果两人同时跳下车,车的运动速度为v1;如果两人是先后跳下车,车的运动速度为v2.则( )
A.一定有v1=v2
B.一定有v1>v2
C.一定有v1D.与m1和m2的大小有关
答案:A
解析:解答:把人、m1、m2和车看成系统,跳前跳后总动量守恒.两人同时跳,则有0=(m1+m2)v+Mv1,所以v1=;两人先后跳,设质量为m1的人先跳,跳后车速为v′,则0=m1v+(m2+M)v′,质量为m2的人后跳,跳后车速为v2,则有:(m2+M)v′=m2v+Mv2,解之得v2=,故A对.
分析:以平板小车和n个人为系统,根据系统动量守恒求解.
根据动量守恒定律,研究第一个人跳下,根据系统动量守恒求出第一个人跳下后小车的速度,依次求出
11.一个人从正在行驶的小车上向前跳下来,小车沿与原运动方向相反的方向驶去,由此可知( )
A.人跳车的速度一定小于小车原来的速度
B.人跳车后的动量一定小于系统原有的总动量
C.人跳车后的动量一定大于系统原有的总动量
D.人给车的冲量一定大于车给人的冲量
答案:C
解析:解答:把人和车看成系统,由动量守恒定律可知:总动量方向是向前的.又因为车后退,C正确.由牛顿第三定律和冲量的定义可知D错.
分析:人与小车组成的系统动量守恒,根据动量守恒定律列方程求解即可
12.一装有柴油的船静止于水面上,船前舱进水,堵住漏洞后用一水泵把前舱的水抽往后舱(如图所示),不计水的阻力,船的运动情况是( )
A.向前运动
B.向后运动
C.静止
D.无法判断
答案:A
解析:解答:不计水的阻力,则系统动量守恒,用一水泵把前舱的水抽往后舱,则水的重心后移,故船将向前运动(等效于人船模型).
分析:水与船组成系统动量守恒,据此分析答题
13.对于下列现象,以下判断正确的是( )
A.喷气式飞机能飞出大气层
B.每秒钟喷出一定量的气体时,喷气速度越大,飞机受到的推力越小
C.战斗开始前扔掉副油箱,在喷气情况相同时,可以飞得更快,操作更灵活
D.以上叙述都不正确
答案:C
解析:解答:因喷气式飞机靠的是从进气道吸入气体然后高速喷出而获得强大的“反推”作用力,故不能飞出大气层,所以A错,B错.根据牛顿第一定律知:减小质量,惯性减小,C对.
分析:一切物体都有保持原来运动状态的性质叫惯性,任何物体都有惯性,物体的惯性大小取决于物体的质量,质量越大,惯性越大,与物体的运动状态及受力情况无关
14.甲、乙两船的质量均为M,它们都静止在平静的湖面上,质量为M的人从甲船跳到乙船上,再从乙船跳回甲船,经过多次跳跃后,最后人在乙船上.假设受的阻力可忽略,则( )
A.甲、乙两船的速度大小之比为3∶2
B.甲、乙两船(包括人)的动量大小之比为2∶1
C.甲、乙两船(包括人)的动量之和为零
D.因跳跃次数未知,故无法判断
答案:C
解析:解答:两船和人组成的系统满足动量守恒.初态动量为零,最后的动量也为零,因此甲、乙两船(包括人)的动量大小一定相等.
分析:对系统应用动量守恒定律求出动量之比,然后求出船的速度之比,根据动量守恒定律求出系统总动量
15.如图所示,质量为M的物体P静止在光滑的水平桌面上,另有一质量为m(M>m)的物体Q以速度v0正对P滑行,则它们相碰后(设桌面足够大)( )
A.Q物体一定被弹回,因为M>m
B.Q物体可能继续向前
C.Q物体的速度不可能为零
D.若相碰后两物体分离,则过一段时间可能再碰
答案:B
解析:解答:因为相碰后Q、P有获得相同速度的可能,所以A错.只有M=m且M、m发生了弹性正碰时,m才可能将动量全部传给M.若M、m发生非弹性碰撞,尽管M>m,但碰后速度仍有可能为零,所以C错.若Q被反向弹回,则Q、P不再相碰,所以D错.
分析:两球滑块在水平方向不受外力,故两滑块组成的系统水平方向的动量守恒.碰撞前后的动量一定守恒,但是动能不一定是守恒的,根据两物体速度的可能的变化进行分析
二.填空题
16.将静置在地面上,质量为M(含燃料)的火箭模型点火升空,在极短时间内以相对地面的速度v0竖直向下喷出质量为m的炽热气体。忽略喷气过程重力和空气阻力的影响,则喷气结束时火箭模型获得的速度大小为 .
答案:mV0/(M—m)
解析:解答:取向上为正方向,由动量守恒定律得:
则火箭速度,
分析:以火箭为研究对象,由动量守恒定律可以求出火箭的速度
17.总质量为M的热气球由于故障在高空以速度v竖直匀速下降,为了阻止其继续下降,在t=0时刻,从热气球中释放了一个质量为m的沙袋.不计空气阻力,当t= 时,热气球停止下降,此时沙袋的速度为 (此时沙袋未着地).
答案:|
解析:解答:因为开始热气球匀速下降,所以热气球受到的浮力等于其重力,即F=Mg,释放沙袋后,对气球由动量定理(选择向下为正方向),有
[(M-m)g-F]·t=0-(M-m)v
时间t=(M-m)v/mg
在沙袋落地之前,对系统(气球及释放的重物)分析,该系统所受合外力为零,所以系统的动量守恒.取竖直向下为正方向,由动量守恒定律得Mv=mv′,解得:v′=Mv/m
即气球的速度减为零时,沙袋的速度为Mv/m.
分析:先根据牛顿第二定律求出热气球释放沙袋后的加速度,根据v=at求停止所用时间;然后根据速度公式可求速度
18.质量为m=60kg的人站在质量为M=100kg的小车上,一起以v=3m/s的速度在光滑水平地面上做匀速直线运动.若人相对车以u=4m/s的速率水平向后跳出,则车的速率变为 .
答案:4.5m/s
解析:解答:取小车的初速度方向为正方向,设人跳出小车时车的速度为v′,则此时人对地的速度为(u+v′).由动量守恒定律得(M+m)v=Mv′+m(u+v′),所以,人向后跳出后,车的速率为v′==4.5m/s(式中u取负值代入).
分析:首先要明确参考系,一般选地面为参考系.其次选择研究的对象,以小车和车上的人组成的系统为研究对象.接着选择正方向,以小车前进的方向为正方向.最关键的是明确系统中各物体的速度大小及方向,跳前系统对地的速度为v0,设跳离时车对地的速度为v,人对地的速度为-u+v.最后根据动量守恒定律列方程求解
19.一质量为6×103kg的火箭从地面竖直向上发射,若火箭喷射燃料气体的速率(相对于火箭)为103m/s,每秒钟喷出 气体才能有克服火箭重力所需的推力,每秒钟喷出
气体才能使火箭在开始时有20m/s2的加速度?(取g=10m/s2)
答案:60kg/s|180kg/s
解析:解答:这是一个反冲现象运动的问题,火箭升空是喷出的气体对火箭反作用力的结果,可以根据动量定理先求出火箭对气体的作用力.(1)以喷出的气体质量为研究对象,设每秒喷出的质量为Δm,火箭对这部分气体的作用力为F,由动量定理有FΔt=Δmv0①
火箭刚要升空时对地速度为零,此时气体相对火箭的速度也就是气体对地的速度,气体对火箭的反作用力F′=F.对火箭(因忽略气体的重力)F′=Mg②
由①②两式解得
kg/s=60kg/s
即要获得克服火箭重力的推力,每秒要喷出60kg的气体.(2)同第(1)问,以喷出的气体Δm为对象.
FΔt=Δmv0③
而对火箭F-Mg=Ma④
由③④两式解得
kg/s=180kg/s.
分析:(1)根据推力的大小,运用动量定理求出每秒喷出的气体.(2)根据牛顿第二定律求出推力的大小,运用动量定理求出每秒喷出气体的质量
20.一个在空中飞行的手雷,以水平速度v飞经离地面高为h的轨道最高点时,炸裂成A、B两块,A、B质量之比为n(少量炸药质量不计)之后,B正好自由下落,A的落地点比不发生爆炸时手雷的落地点远 爆炸前后机械能变化了 。
答案:|增加
解析:解答:爆炸前后动量守恒,有mv=mAvA
得
爆炸后,A以vA做平抛运动,运动时间
射程的增加量Δs为
此题爆炸前后可认为动量守恒,但机械能并不?守恒?,
.机械能是增加的,这一点与碰撞过程不同.
分析:根据两块爆竹爆炸时水平方向动量守恒求出大块爆竹的速度,然后根据平抛运动求出时间和水平位移
三.计算题
21.质量为4t的火箭,其喷出气体对地的速度为500m/s,则:
(1)它至少每秒喷出质量为多少的气体,才能开始上升?
答案:当喷出的气体对火箭的平均冲力大于重力时,火箭才能开始上升.由F=>(M-m)g,t=1s,得m>+g=78.4kg.
(2)如果要以2m/s2的加速度上升,则每秒可喷出多少气体?
答案:设a=2m/s2时,每秒喷出气体的质量为m′,则由牛顿运动定律得,-(M-m′)g=(M-m′)a,t=1s,求出m′==93.8kg
(3)火箭上升后,由于继续喷气,火箭质量将逐渐变小,如果喷气对地速度保持不变,要维持不变的上升加速度,则每秒喷出的气体的质量应如何变化?取g=10m/s2.
答案:由-(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=-g=-g,要使a保持不变,只有使每秒喷出气体的质量m′减小
解析:解答:(1)当喷出的气体对火箭的平均冲力大于重力时,火箭才能开始上升.由F=>(M-m)g,t=1s,得m>+g=78.4kg.(2)设a=2m/s2时,每秒喷出气体的质量为m′,则由牛顿运动定律得,-(M-m′)g=(M-m′)a,t=1s,求出m′==93.8kg.(3)由-(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=-g=-g,要使a保持不变,只有使每秒喷出气体的质量m′减小.
分析:对气体分析由动量定理可求得反冲现象力与动量的关系;再对火箭分析可求得加速度与力的关系,联立可求
22.一门旧式大炮,炮身的质量为M,射出的炮弹的质量为m,对地的速度为v,方向与水平方向成α角.若不计炮身与水平地面间的摩擦,则炮身后退的速度多大
答案:解答:在发射炮弹的过程中,炮身和炮弹的总动量不守恒(由于斜向上发射炮弹,所以地面对炮身的支持力大于它们的重力).但在水平方向,系统并没受到外力,所以可把系统的动量沿水平方向和竖直方向分解,其水平分量保持不变.由水平方向的动量守恒知MV-mvcosα=0,炮身后退的速度为V=vcosα.
解析:解答:在发射炮弹的过程中,炮身和炮弹的总动量不守恒(由于斜向上发射炮弹,所以地面对炮身的支持力大于它们的重力).但在水平方向,系统并没受到外力,所以可把系统的动量沿水平方向和竖直方向分解,其水平分量保持不变.由水平方向的动量守恒知MV-mvcosα=0,炮身后退的速度为V=vcosα.
分析:对炮弹和炮身组成的系统,火炮发射炮弹的过程中,在水平方向受到的外力可忽略不计,在水平方向动量守恒,列式可求得炮弹离开炮口时炮车后退速度
23.一总质量M=300kg的火箭,每次喷出气体的质量为m=200g,每次喷气的速度(相对地面)均为v=1000m/s.假设火箭开始处于静止状态,每次喷气时间极短,则第二次气体喷出后火箭水平飞行的速度为多大?
答案:解答:由于题设条件每次喷气的对地速度相同,因此,分批喷出后火箭的速度与这些气体一起一次喷出时火箭获得的速度是一样的.即由
0=(M-2m)v2-2mv,得
v2=v=×1000m/s=1.335m/s.
解析:解答:由于题设条件每次喷气的对地速度相同,因此,分批喷出后火箭的速度与这些气体一起一次喷出时火箭获得的速度是一样的.即由
0=(M-2m)v2-2mv,得
v2=v=×1000m/s=1.335m/s.
分析:以火箭为研究对象,由动量守恒定律可以求出火箭的速度
24.“神舟”六号宇宙飞船是由火箭喷气发动机向后喷气而加速的.假设火箭喷气发动机每次喷出气体质量为m,喷出的气体相对地面的速度为v,设“神舟”六号载人飞船及火箭的总质量为M(m<答案:解答:选火箭和1s内喷出的气体为研究对象,设火箭1s末的速度为v′,1s内共喷出质量为20m的气体,取火箭运动方向为正方向,由动量守恒定律得
(M-20m)v′-20mv=0
所以1s末火箭的速度v′=.
解析:解答:选火箭和1s内喷出的气体为研究对象,设火箭1s末的速度为v′,1s内共喷出质量为20m的气体,取火箭运动方向为正方向,由动量守恒定律得
(M-20m)v′-20mv=0
所以1s末火箭的速度v′=.
分析:以火箭整体为研究对象,由动量守恒定律可以求出火箭的速度
25.倾角为θ、长为L的斜面置于光滑水平面上,如图所示.已知斜面质量为M,今有一质量为m的滑块从斜面上端开始下滑,求滑块滑到底端时,斜面后退的位移大小.
答案:解答:在两物体相互作用的过程中,水平方向上动量时时守恒,其速度可取平均速度,本题可取后退方向为正方向,列动量守恒方程:0=M·,即s=.
解析:解答:在两物体相互作用的过程中,水平方向上动量时时守恒,其速度可取平均速度,本题可取后退方向为正方向,列动量守恒方程:0=M·,即s=.
分析:对于物体在水平面上滑行过程,运用动量守恒求解物体在水平面上滑过的距离
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
人教版物理高三选修3-5第十六章
第五节反冲运动 火箭同步训练
一.选择题
1.如图所示,光滑平面上有一辆质量为2m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度vo向右匀速运动。某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车。两人都离开小车后,小车的速度将是( )
A.vo B.2vo C.大于vo,小于2vo D.大于2vo
答案:B
解析:解答:两人和车所组成的系统动量守恒,初动量为4mv,方向向右。当甲、乙两人先后以对地相等的速度向两个方向跳离时,甲、乙两人的动量和为零,则有4mv=2mv车,v车=2v;,选项B正确。
分析:车和两个人整体在水平方向不受外力,系统总动量守恒,根据动量守恒定律列式求解即可
2.下列属于反冲现象运动的是( )
A.汽车的运动 B.直升飞机的运动
C.火箭发射过程的运动 D.自行车的运动
答案:C
解析:解答:反冲现象是根据动量守恒,物体分为两部分,一部分向一个方向运动,另一部分向反方向运动。符合条件的为C选项。
分析:本题考查反冲现象运动的应用;明确反冲现象运动是相互作用的物体之间的作用力与反作用力产生的效果
3.下列几种现象中,动量不守恒的是( )
A.在光滑水平面上两球发生碰撞
B.车原来静止在光滑的水平面上,车上的人从车头走到车尾
C.水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动
D.火箭的反冲现象运动
答案:C
解析:解答:在光滑水平面上两球发生碰撞,系统所受合外力为零,故动量守恒车原来静止在光滑的水平面上,车上的人从车头走到车尾,系统所受合外力为零,故动量守恒
水平放置的弹簧一端固定,另一端与置于光滑水平面的物体相连,伸长的弹簧拉物体运动,系统所受合外力不为零,故动量不守恒火箭的反冲现象运动,系统内力远大于外力,故动量守恒选动量不守恒的情况,所以选C
分析:动量守恒的条件是:系统所受合外力为零,或者系统内力远大于外力情况
4.在光滑水平面上有两辆车,上面分别站着A、B两个人,人与车的质量总和相等,在A的手中拿有一个球,两车均保持静止状态.当A将手中球抛给B,B接到后,又抛给A,如此反复多次,最后球落在B的手中.则关于A、B速率的大小是( )
A.A、B两车速率相等
B.A车速率大
C.A车速率小
D.两车均保持静止状态
答案:B
解析:解答:由动量守恒可知,总动量始终为零,则两辆车(包括各自车上站的人)的动量大小相等,方向相反.这样质量大的速度就小,最后球在B车上,所以A车速度大.?
分析:以整体为研究对象,水平方向动量守恒,依据动量守恒列方程即可判断二者速度的大小
5.如图所示,一个质量为m的玩具蛙蹲在质量为m′的小车的细杆上,小车放在光滑的水平桌面上.若车长为,细杆高为h,且位于小车的中点,则玩具蛙至少以多大的水平速度v0跳出时,才能落到桌面上( )
A.v B.3 C.2 D.
答案:D
解析:解答:设蛙水平跳出速度为v0,小车后退速度为v1,则与蛙在车作用过程中,系统水平方向动量守恒,则
0=mv0-m′v1(以v0方向为正).
在蛙未落至桌面前,小车以v1做匀速运动,设t内走x,则
x=v1·t(x为对地位移).
在t时间内,蛙做平抛运动,根据平抛运动规律,即
,蛙对地的水平位移应为,而至少应为.
解以上各式得.
分析:车与蛙系统动量守恒,蛙跳出后做平抛运动,应用动量守恒定律与平抛运动规律求出速度
6.一个人在地面上立定跳远最好成绩是s.假设他站在静止于地面的小车的A端(车与地面的摩擦不计),如图所示,他欲从A端跳上L远处的站台上,则……( )
A.只要L
D.只要L=s,他有可能跳上站台
答案:B
解析:解答:由于反冲现象作用,运动员从车上起跳的最好成绩一定小于s,故选项B正确.
分析:当人往站台上跳的时候,人有一个向站台的速度,由于动量守恒,车子必然有一个离开站台的速度.
这样的话,如果L=S或L>S,人就一定跳不到站台上了,L<S,人才有可能跳上站台
7.人静止于光滑冰面上,现欲前进,下列方法中可行的是( )
A.向后踢腿
B.手臂向前甩
C.在冰上滚
D.脱去外衣向后投掷
答案:D
解析:解答:欲使物体获得一定的动量,必须有外力作用在该物体上.A、B两种方法属于物体两部分间的作用,不会对物体产生冲量;因冰面是光滑的,故C也不行.
分析:选取合适的系统为研究对象,根据动量守恒定律进行分析
8.假设一小型火箭沿人造地球卫星的轨道在高空中做匀速圆周运动.如果火箭向跟其速度相反的方向射出一个质量不可忽略的物体A,则下列情况哪些是能够成立的( )
A.物体A可能竖直落下地球,火箭可能沿原轨道运动
B.A跟火箭都不可能沿原轨道运动
C.A运行轨道半径将减小,火箭运动轨道半径将减小
D.A可能沿地球半径方向竖直下落,火箭运行的轨道半径增大
答案:D
解析:解答:火箭绕地球做匀速圆周运动时,万有引力刚好充当向心力,在轨迹切线方向无外力作用,故火箭沿切线向后发射物体过程中,系统沿轨道切线方向动量守恒,所以v′>v0.所以火箭要做离心运动,即火箭不可能在原轨道上运行.至于被发射的物体A,由于发射时做功情况的不同,发射后的A,速度可沿原运动方向,但速度变小,要做向心运动,即轨道半径变小;速度也可能刚好为零(对地),以后则竖直下落;速度也可能大小刚好等于火箭原飞行速度,所以A也可能在原轨道上运行,只是绕行方向与火箭绕行方向相反.综上讨论可知,正确选项为D.
分析:整个过程中系统动量守恒,而抛出后A的速度方向有几种可能,根据抛出后A的速度的大小和方向结合向心力的知识判断A物体的运动情况
9.一人静止于光滑的水平冰面上,现欲离开冰面,下列方法中可行的是( )
A.向后踢腿 B.手臂向后甩 C.在冰面上滚动 D.脱下外衣水平抛出
答案:D
解析:解答:把人和外衣看作系统,由动量守恒定律可知:衣服向后抛出时,人会向前反冲现象,故D对.由于人体各部分总动量为零,故A、B皆错.由于冰面“光滑”,故人不可能在冰面上滚动,D错.
分析:选取合适的系统为研究对象,根据动量守恒定律进行分析
10.在光滑水平面上停放着一辆平板车,车上站着质量分别为m1和m2的两个人.现两人都以相同的对地速度,从车尾跳下车.如果两人同时跳下车,车的运动速度为v1;如果两人是先后跳下车,车的运动速度为v2.则( )
A.一定有v1=v2
B.一定有v1>v2
C.一定有v1
答案:A
解析:解答:把人、m1、m2和车看成系统,跳前跳后总动量守恒.两人同时跳,则有0=(m1+m2)v+Mv1,所以v1=;两人先后跳,设质量为m1的人先跳,跳后车速为v′,则0=m1v+(m2+M)v′,质量为m2的人后跳,跳后车速为v2,则有:(m2+M)v′=m2v+Mv2,解之得v2=,故A对.
分析:以平板小车和n个人为系统,根据系统动量守恒求解.
根据动量守恒定律,研究第一个人跳下,根据系统动量守恒求出第一个人跳下后小车的速度,依次求出
11.一个人从正在行驶的小车上向前跳下来,小车沿与原运动方向相反的方向驶去,由此可知( )
A.人跳车的速度一定小于小车原来的速度
B.人跳车后的动量一定小于系统原有的总动量
C.人跳车后的动量一定大于系统原有的总动量
D.人给车的冲量一定大于车给人的冲量
答案:C
解析:解答:把人和车看成系统,由动量守恒定律可知:总动量方向是向前的.又因为车后退,C正确.由牛顿第三定律和冲量的定义可知D错.
分析:人与小车组成的系统动量守恒,根据动量守恒定律列方程求解即可
12.一装有柴油的船静止于水面上,船前舱进水,堵住漏洞后用一水泵把前舱的水抽往后舱(如图所示),不计水的阻力,船的运动情况是( )
A.向前运动
B.向后运动
C.静止
D.无法判断
答案:A
解析:解答:不计水的阻力,则系统动量守恒,用一水泵把前舱的水抽往后舱,则水的重心后移,故船将向前运动(等效于人船模型).
分析:水与船组成系统动量守恒,据此分析答题
13.对于下列现象,以下判断正确的是( )
A.喷气式飞机能飞出大气层
B.每秒钟喷出一定量的气体时,喷气速度越大,飞机受到的推力越小
C.战斗开始前扔掉副油箱,在喷气情况相同时,可以飞得更快,操作更灵活
D.以上叙述都不正确
答案:C
解析:解答:因喷气式飞机靠的是从进气道吸入气体然后高速喷出而获得强大的“反推”作用力,故不能飞出大气层,所以A错,B错.根据牛顿第一定律知:减小质量,惯性减小,C对.
分析:一切物体都有保持原来运动状态的性质叫惯性,任何物体都有惯性,物体的惯性大小取决于物体的质量,质量越大,惯性越大,与物体的运动状态及受力情况无关
14.甲、乙两船的质量均为M,它们都静止在平静的湖面上,质量为M的人从甲船跳到乙船上,再从乙船跳回甲船,经过多次跳跃后,最后人在乙船上.假设受的阻力可忽略,则( )
A.甲、乙两船的速度大小之比为3∶2
B.甲、乙两船(包括人)的动量大小之比为2∶1
C.甲、乙两船(包括人)的动量之和为零
D.因跳跃次数未知,故无法判断
答案:C
解析:解答:两船和人组成的系统满足动量守恒.初态动量为零,最后的动量也为零,因此甲、乙两船(包括人)的动量大小一定相等.
分析:对系统应用动量守恒定律求出动量之比,然后求出船的速度之比,根据动量守恒定律求出系统总动量
15.如图所示,质量为M的物体P静止在光滑的水平桌面上,另有一质量为m(M>m)的物体Q以速度v0正对P滑行,则它们相碰后(设桌面足够大)( )
A.Q物体一定被弹回,因为M>m
B.Q物体可能继续向前
C.Q物体的速度不可能为零
D.若相碰后两物体分离,则过一段时间可能再碰
答案:B
解析:解答:因为相碰后Q、P有获得相同速度的可能,所以A错.只有M=m且M、m发生了弹性正碰时,m才可能将动量全部传给M.若M、m发生非弹性碰撞,尽管M>m,但碰后速度仍有可能为零,所以C错.若Q被反向弹回,则Q、P不再相碰,所以D错.
分析:两球滑块在水平方向不受外力,故两滑块组成的系统水平方向的动量守恒.碰撞前后的动量一定守恒,但是动能不一定是守恒的,根据两物体速度的可能的变化进行分析
二.填空题
16.将静置在地面上,质量为M(含燃料)的火箭模型点火升空,在极短时间内以相对地面的速度v0竖直向下喷出质量为m的炽热气体。忽略喷气过程重力和空气阻力的影响,则喷气结束时火箭模型获得的速度大小为 .
答案:mV0/(M—m)
解析:解答:取向上为正方向,由动量守恒定律得:
则火箭速度,
分析:以火箭为研究对象,由动量守恒定律可以求出火箭的速度
17.总质量为M的热气球由于故障在高空以速度v竖直匀速下降,为了阻止其继续下降,在t=0时刻,从热气球中释放了一个质量为m的沙袋.不计空气阻力,当t= 时,热气球停止下降,此时沙袋的速度为 (此时沙袋未着地).
答案:|
解析:解答:因为开始热气球匀速下降,所以热气球受到的浮力等于其重力,即F=Mg,释放沙袋后,对气球由动量定理(选择向下为正方向),有
[(M-m)g-F]·t=0-(M-m)v
时间t=(M-m)v/mg
在沙袋落地之前,对系统(气球及释放的重物)分析,该系统所受合外力为零,所以系统的动量守恒.取竖直向下为正方向,由动量守恒定律得Mv=mv′,解得:v′=Mv/m
即气球的速度减为零时,沙袋的速度为Mv/m.
分析:先根据牛顿第二定律求出热气球释放沙袋后的加速度,根据v=at求停止所用时间;然后根据速度公式可求速度
18.质量为m=60kg的人站在质量为M=100kg的小车上,一起以v=3m/s的速度在光滑水平地面上做匀速直线运动.若人相对车以u=4m/s的速率水平向后跳出,则车的速率变为 .
答案:4.5m/s
解析:解答:取小车的初速度方向为正方向,设人跳出小车时车的速度为v′,则此时人对地的速度为(u+v′).由动量守恒定律得(M+m)v=Mv′+m(u+v′),所以,人向后跳出后,车的速率为v′==4.5m/s(式中u取负值代入).
分析:首先要明确参考系,一般选地面为参考系.其次选择研究的对象,以小车和车上的人组成的系统为研究对象.接着选择正方向,以小车前进的方向为正方向.最关键的是明确系统中各物体的速度大小及方向,跳前系统对地的速度为v0,设跳离时车对地的速度为v,人对地的速度为-u+v.最后根据动量守恒定律列方程求解
19.一质量为6×103kg的火箭从地面竖直向上发射,若火箭喷射燃料气体的速率(相对于火箭)为103m/s,每秒钟喷出 气体才能有克服火箭重力所需的推力,每秒钟喷出
气体才能使火箭在开始时有20m/s2的加速度?(取g=10m/s2)
答案:60kg/s|180kg/s
解析:解答:这是一个反冲现象运动的问题,火箭升空是喷出的气体对火箭反作用力的结果,可以根据动量定理先求出火箭对气体的作用力.(1)以喷出的气体质量为研究对象,设每秒喷出的质量为Δm,火箭对这部分气体的作用力为F,由动量定理有FΔt=Δmv0①
火箭刚要升空时对地速度为零,此时气体相对火箭的速度也就是气体对地的速度,气体对火箭的反作用力F′=F.对火箭(因忽略气体的重力)F′=Mg②
由①②两式解得
kg/s=60kg/s
即要获得克服火箭重力的推力,每秒要喷出60kg的气体.(2)同第(1)问,以喷出的气体Δm为对象.
FΔt=Δmv0③
而对火箭F-Mg=Ma④
由③④两式解得
kg/s=180kg/s.
分析:(1)根据推力的大小,运用动量定理求出每秒喷出的气体.(2)根据牛顿第二定律求出推力的大小,运用动量定理求出每秒喷出气体的质量
20.一个在空中飞行的手雷,以水平速度v飞经离地面高为h的轨道最高点时,炸裂成A、B两块,A、B质量之比为n(少量炸药质量不计)之后,B正好自由下落,A的落地点比不发生爆炸时手雷的落地点远 爆炸前后机械能变化了 。
答案:|增加
解析:解答:爆炸前后动量守恒,有mv=mAvA
得
爆炸后,A以vA做平抛运动,运动时间
射程的增加量Δs为
此题爆炸前后可认为动量守恒,但机械能并不?守恒?,
.机械能是增加的,这一点与碰撞过程不同.
分析:根据两块爆竹爆炸时水平方向动量守恒求出大块爆竹的速度,然后根据平抛运动求出时间和水平位移
三.计算题
21.质量为4t的火箭,其喷出气体对地的速度为500m/s,则:
(1)它至少每秒喷出质量为多少的气体,才能开始上升?
答案:当喷出的气体对火箭的平均冲力大于重力时,火箭才能开始上升.由F=>(M-m)g,t=1s,得m>+g=78.4kg.
(2)如果要以2m/s2的加速度上升,则每秒可喷出多少气体?
答案:设a=2m/s2时,每秒喷出气体的质量为m′,则由牛顿运动定律得,-(M-m′)g=(M-m′)a,t=1s,求出m′==93.8kg
(3)火箭上升后,由于继续喷气,火箭质量将逐渐变小,如果喷气对地速度保持不变,要维持不变的上升加速度,则每秒喷出的气体的质量应如何变化?取g=10m/s2.
答案:由-(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=-g=-g,要使a保持不变,只有使每秒喷出气体的质量m′减小
解析:解答:(1)当喷出的气体对火箭的平均冲力大于重力时,火箭才能开始上升.由F=>(M-m)g,t=1s,得m>+g=78.4kg.(2)设a=2m/s2时,每秒喷出气体的质量为m′,则由牛顿运动定律得,-(M-m′)g=(M-m′)a,t=1s,求出m′==93.8kg.(3)由-(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=-g=-g,要使a保持不变,只有使每秒喷出气体的质量m′减小.
分析:对气体分析由动量定理可求得反冲现象力与动量的关系;再对火箭分析可求得加速度与力的关系,联立可求
22.一门旧式大炮,炮身的质量为M,射出的炮弹的质量为m,对地的速度为v,方向与水平方向成α角.若不计炮身与水平地面间的摩擦,则炮身后退的速度多大
答案:解答:在发射炮弹的过程中,炮身和炮弹的总动量不守恒(由于斜向上发射炮弹,所以地面对炮身的支持力大于它们的重力).但在水平方向,系统并没受到外力,所以可把系统的动量沿水平方向和竖直方向分解,其水平分量保持不变.由水平方向的动量守恒知MV-mvcosα=0,炮身后退的速度为V=vcosα.
解析:解答:在发射炮弹的过程中,炮身和炮弹的总动量不守恒(由于斜向上发射炮弹,所以地面对炮身的支持力大于它们的重力).但在水平方向,系统并没受到外力,所以可把系统的动量沿水平方向和竖直方向分解,其水平分量保持不变.由水平方向的动量守恒知MV-mvcosα=0,炮身后退的速度为V=vcosα.
分析:对炮弹和炮身组成的系统,火炮发射炮弹的过程中,在水平方向受到的外力可忽略不计,在水平方向动量守恒,列式可求得炮弹离开炮口时炮车后退速度
23.一总质量M=300kg的火箭,每次喷出气体的质量为m=200g,每次喷气的速度(相对地面)均为v=1000m/s.假设火箭开始处于静止状态,每次喷气时间极短,则第二次气体喷出后火箭水平飞行的速度为多大?
答案:解答:由于题设条件每次喷气的对地速度相同,因此,分批喷出后火箭的速度与这些气体一起一次喷出时火箭获得的速度是一样的.即由
0=(M-2m)v2-2mv,得
v2=v=×1000m/s=1.335m/s.
解析:解答:由于题设条件每次喷气的对地速度相同,因此,分批喷出后火箭的速度与这些气体一起一次喷出时火箭获得的速度是一样的.即由
0=(M-2m)v2-2mv,得
v2=v=×1000m/s=1.335m/s.
分析:以火箭为研究对象,由动量守恒定律可以求出火箭的速度
24.“神舟”六号宇宙飞船是由火箭喷气发动机向后喷气而加速的.假设火箭喷气发动机每次喷出气体质量为m,喷出的气体相对地面的速度为v,设“神舟”六号载人飞船及火箭的总质量为M(m<
(M-20m)v′-20mv=0
所以1s末火箭的速度v′=.
解析:解答:选火箭和1s内喷出的气体为研究对象,设火箭1s末的速度为v′,1s内共喷出质量为20m的气体,取火箭运动方向为正方向,由动量守恒定律得
(M-20m)v′-20mv=0
所以1s末火箭的速度v′=.
分析:以火箭整体为研究对象,由动量守恒定律可以求出火箭的速度
25.倾角为θ、长为L的斜面置于光滑水平面上,如图所示.已知斜面质量为M,今有一质量为m的滑块从斜面上端开始下滑,求滑块滑到底端时,斜面后退的位移大小.
答案:解答:在两物体相互作用的过程中,水平方向上动量时时守恒,其速度可取平均速度,本题可取后退方向为正方向,列动量守恒方程:0=M·,即s=.
解析:解答:在两物体相互作用的过程中,水平方向上动量时时守恒,其速度可取平均速度,本题可取后退方向为正方向,列动量守恒方程:0=M·,即s=.
分析:对于物体在水平面上滑行过程,运用动量守恒求解物体在水平面上滑过的距离
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
