初中数学北师大版八年级下册 1.1 等腰三角形小节复习题 (含解析)
文档属性
| 名称 | 初中数学北师大版八年级下册 1.1 等腰三角形小节复习题 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览

文档简介
1.1 等腰三角形小节复习题
【题型1 利用等边对等角求解】
1.如图,四边形中,,将沿着折叠,点B恰好落在边上的点处.若,则可表示为( )
A. B. C. D.
2.某平板电脑支架如图所示,其中,,为了使用的舒适性,可调整的大小.若增大,则的变化情况是( )
A.增大 B.减小 C.增大 D.减小
3.如图,与关于对称,,在上取一点,使得.若,则的度数是()
A. B. C. D.
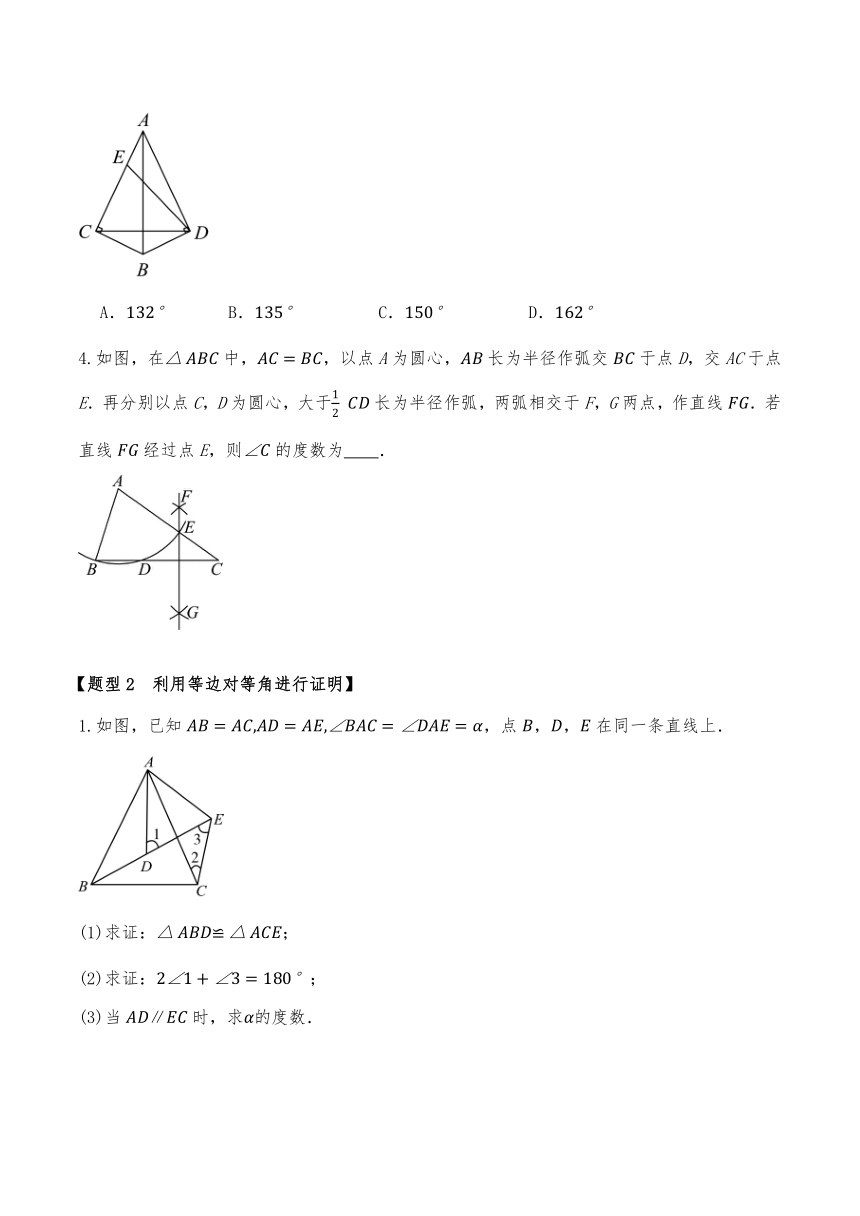
4.如图,在中,,以点A为圆心,长为半径作弧交于点D,交AC于点E.再分别以点C,D为圆心,大于 长为半径作弧,两弧相交于F,G两点,作直线.若直线经过点E,则的度数为 .
【题型2 利用等边对等角进行证明】
1.如图,已知,点,,在同一条直线上.
(1)求证:;
(2)求证:;
(3)当时,求的度数.
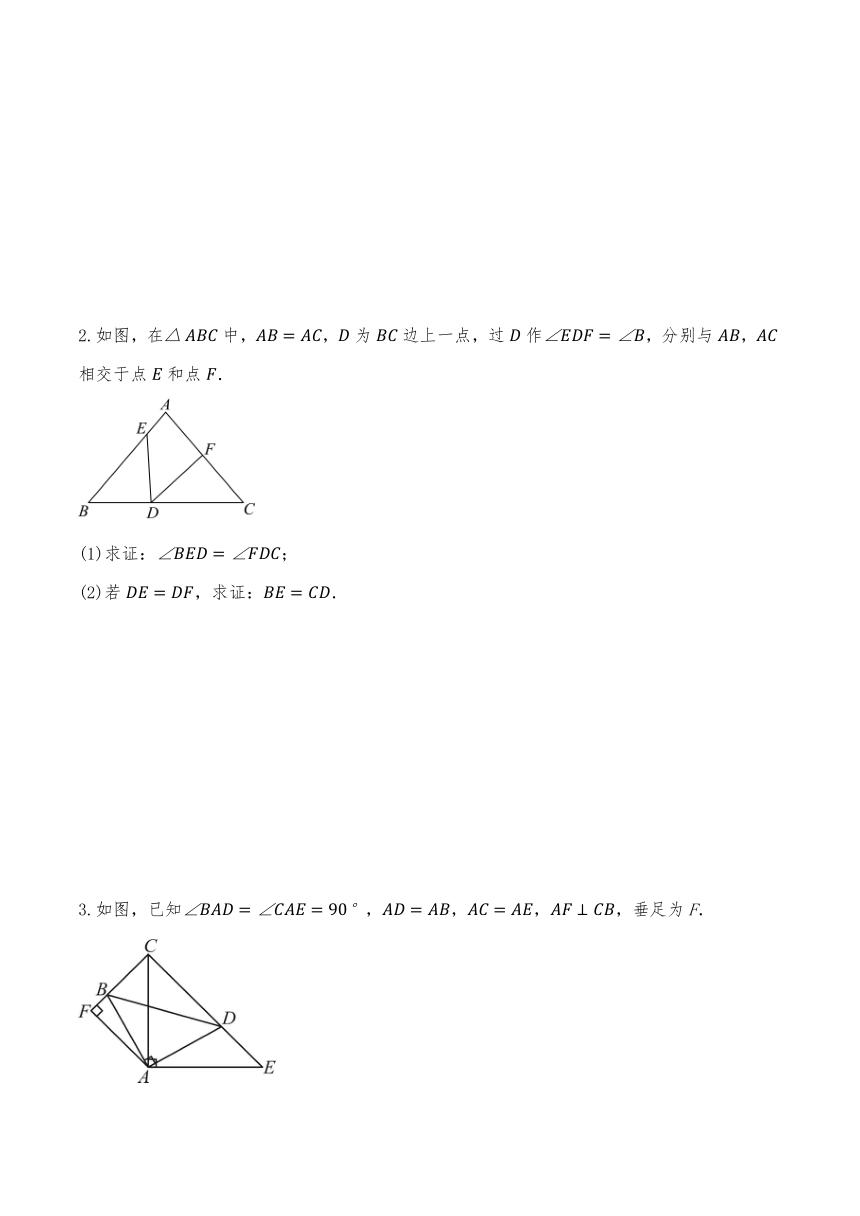
2.如图,在中,,为边上一点,过作,分别与,相交于点和点.
(1)求证:;
(2)若,求证:.
3.如图,已知,,,,垂足为F.
(1)求证:;
(2)已知 ,求证:.
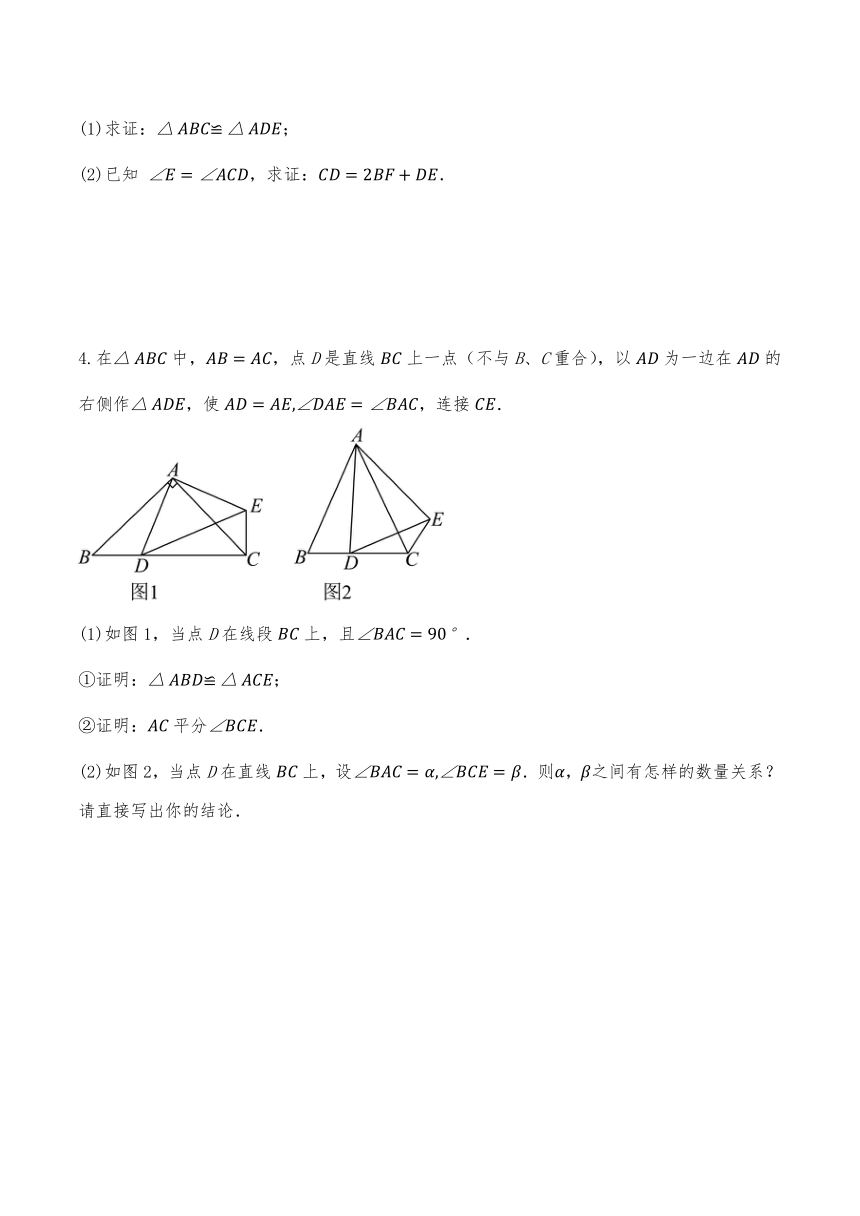
4.在中,,点D是直线上一点(不与B、C重合),以为一边在的右侧作,使,连接.
(1)如图1,当点D在线段上,且.
①证明:;
②证明:平分.
(2)如图2,当点D在直线上,设.则,之间有怎样的数量关系?请直接写出你的结论.
【题型3 利用三线合一求解】
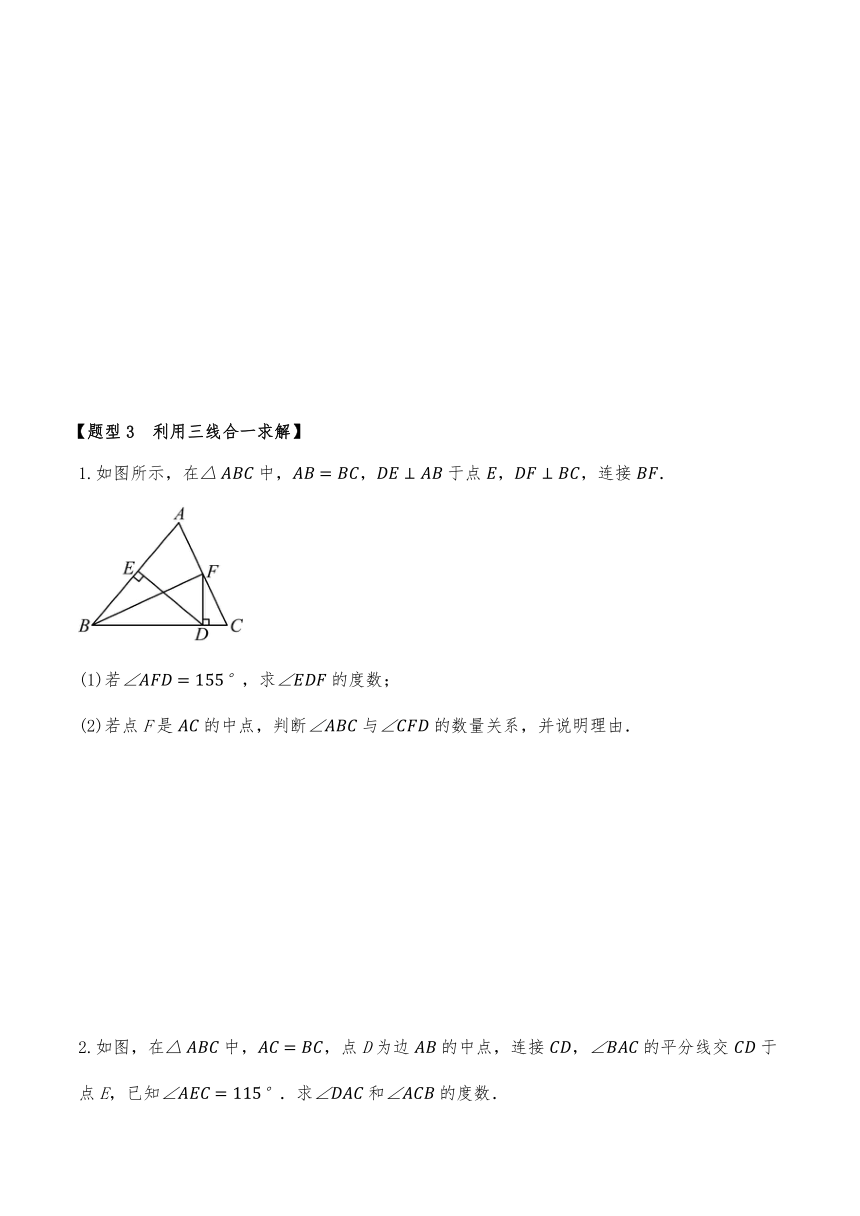
1.如图所示,在中,,于点,,连接.
(1)若,求的度数;
(2)若点F是的中点,判断与的数量关系,并说明理由.
2.如图,在中,,点D为边的中点,连接,的平分线交于点E,已知.求和的度数.
3.如图,在中,,是边上的中线,的垂直平分线分别交、、于点、、,连接,.
(1)试说明:;
(2)若,求的度数.
4.如图,在中,,是的中点,垂直平分,交于点,交于点,是直线上的动点.
(1)当时,
①若,则点到的距离为________;
②若,,求的周长;
(2)若,且的面积为40,求周长的最小值.
【题型4 利用三线合一证明】
1.如图,在中,是边上的高线,是中线,且于,.
(1)求证:是的中点;
(2)求证.
2.如图,在中,的垂直平分线交于点,交于点,为线段的中点,.
(1)求证:;
(2)若,则的度数为 ___________.
3.如图,为线段 上一点, ,,, 平分 .
(1)求证:;
(2)问: 与 的位置关系并证明.
4.已知:如图,在中,,,于点,将沿折叠,使点A落在直线上的点处,是的平分线,交于点,交于点,连接.
(1)吗?为什么?
(2)试说明垂直平分.
【题型5 格点中画等腰三角形】
1.如图,在的网格中,每个网格线的交点称为格点.已知图中,两个格点,请在图中再寻找另一个格点,使成为等腰三角形,则满足条件的点有( )个.
A. B. C. D.
2.在方格纸中,点P、Q都在格点上,请用无刻度的直尺按要求画格点三角形:
(1)在图1中,画一个以为腰的等腰(为格点);
(2)在图2中,画一个以为底的等腰(为格点).
3.如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个等腰,且使得点为格点.请在下面的网格图中画出3种不同的等腰.
4.图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图1、图2、图3给定的网格中按要求作图.
要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
(1)在图1中的格点上确定一点P,画一个以AB为腰的等腰△ABP.
(2)在图2中的格点上确定一点P,画一个以AB为底的等腰△ABP.
(3)在图3中的格线MN上确定一点P,使PA与PB的长度之和最小.
【题型6 找出图中的等腰三角形】
1.如图,在中,,的垂直平分线交于点D、E,则图中等腰三角形的个数是( )
A.2 B.3 C.4 D.5
2.如图,在中,已知边的垂直平分线与边的垂直平分线交于点,连接,则图中有 个等腰三角形.
3.如图,在四边形中,,,,点E是线段上一点,且.
(1)求证:;
(2)直接写出图中所有的等腰三角形.
4.如图,中,,,平分,于点,连结交于点,则图中的等腰三角形有( )
A.2个 B.3个 C.4个 D.5个
【题型7 利用等角对等边证明等腰三角形】
1.如图,在中,,,边的垂直平分线与交于点,与交于点,连接.求证:是等腰三角形.
2.如图,在中,,是斜边上的高,角平分线交于点.求证:是等腰三角形.
3.如图,,点分别在,上,以,为边在内作等边三角形,,连接并延长交于点,求证:.
4.如图,在中,,,与的角平分线、分别交、边于点D和点E.
(1)求证:是等腰三角形;
(2)用等式表示线段之间的数量关系,并证明.
【题型8 利用等角对等边求边长或证明边相等】
1.如图,在中,,分别是和的平分线,,交于点D,于点F.若,,,则的面积为( )
A.50 B.55 C.60 D.65
2.如图,,,交于F,交于点E,求证:.
3.如图,在中,,和的平分线分别交于点、,若,,,,则 .
4.已知:如图,点D是的边上的一点,过点D作,,垂足分别为E、F,再过点D作,交于点G,且.
求证:
(1);
(2).
【题型9 尺规作等腰三角形】
1.如图,已知一个等腰三角形的底边为c,底边上的高为,求作这个等腰三角形.(保留作图痕迹,不必写作法)
2.如图,已知,点B是射线上一点,求作等腰三角形,使得为等腰三角形的底边,点A在内部,且点A到角的两边距离相等.(尺规作图)
3.如图.已知一个含有角的直角三角形,请利用它用两种不同的方法构造一个含角的直角三角形.(尺规作图,不写做法,保留作图轨迹)
4.证明:等腰三角形的两底角相等.要求:
(1)用无刻度的直尺和圆规作等腰,使底边,腰;
(2)结合图形,写出已知、求证,并完成证明;
(3)证明过程若需添加辅助线,则辅助线也需用无刻度的直尺和圆规作图.
【题型10 确定与已知两点构成等腰三角形的点】
1.如图所示,在中,,,点D在CA上,且,动点P从A点出发沿A→B→C的路线运动,运动到点C停止.在点P的运动过程中,使为等腰三角形的点P有 个.
2.如图所示,在长方形的对称轴上找点,使得、均为等腰三角形,则满足条件的点的个数是( )
A.2 B.3 C.4 D.5
3.如图,已知中,.在直线或上取一点P,使得是等腰三角形,则符合条件的P点有 个.
4.如图,线段的一个端点B在直线m上,直线m上存在点C,使为等腰三角形,这样的点C有( )
A.2个 B.3个 C.4个 D.5个
参考答案
【题型1 利用等边对等角求解】
1.B
【分析】本题考查了折叠的性质,等腰三角形的性质,三角形外角的性质;由折叠得,,由等腰三角形的性质得,由三角形外角的性质得 ,即可求解;掌握折叠的性质,等腰三角形的性质是解题的关键.
【详解】解:由折叠得:
,
,
,
,
,
,
,
,
,
,
故选:B.
2.D
【分析】本题考查了等腰三角形的性质,三角形内角和定理等知识,设设原来,求出此时,然后类似求出变化后,然后两角作差即可得出结论.
【详解】解:设原来,则
∵,
∴,
∴,
增大后,,
∴,
∴,
∴,
∴的变化情况是减小,
故选:D.
3.A
【分析】本题考查了轴对称性质、等腰三角形的性质及直角三角形的性质,解决本题的关键是熟练掌握轴对称性质、等腰三角形的性质及直角三角形的性质,由轴对称性质得,
设,得出,再由等腰三角形的性质得.再由直角三角形的性质列出方程求解即可.
【详解】解:与关于对称,
,
设.
,
在中,,
.
又,
,
,
故选:A
4.
【分析】本题考查了作图复杂作图,线段垂直平分线的性质和等腰三角形的性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作. 连接、,如图,设,利用基本作图得到,则,所以,再根据等腰三角形的性质和三角形内角和得到,接着利用得到,则根据求出.
【详解】解:连接、,如图,设,
由作法得垂直平分,
,
,
,
,,
,
,,
,,
,
,
解得,
.
故答案为:.
【题型2 利用等边对等角进行证明】
1.(1)证明:,
,
即,
在和中,
,
;
(2)证明:,
,
,
,
,
,
;
(3)解:,
,
,
,
,
.
2.(1)∵,
∴,
又∵,,
∴;
(2)在和中
,
∴,
∴.
3.(1)∵,
∴,,
∴,
在和中,
,
∴.
(2)如图,延长到G,使,连接,
∵,
∴,
∴,
∵,
∴,
由(1)得:,
,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴.
4.(1)证明:① ,
,
,
在和中,
,
;
② 中,,
,
由①得,
,
,
平分.
(2)解:,
①点D在线段上,如图:
,
,
,
在和中,
,
;
,
在中,,
∴,
∴,
∵,
∴;
②当点D在射线上时,如图:
,
,
,
在和中,
,
,
,
在中,,
∴,
∴,
∵,
∴;
③当点D在射线上时,如图:
同理可得 ,
∴,
在中,,
∴,
∴.
∵,
∴;
综上所述α,β之间的数量关系为:或.
【题型3 利用三线合一求解】
1.(1)解:∵,
∴,
∵,,
∴,
在Rt△FDC中,
∴,
∵,
∴,
∴,
∵,
∴;
(2),理由如下:
∵,且点F是的中点,
∴,,
∴,,
∴,
∴.
2.解:∵,点D为边的中点,
∴,,
∴,
∵,,
∴,
∵是的平分线,
∴,
在中,
,
∴.
3.(1)因为,点是的中点,
所以,所以是的垂直平分线,
所以,
因为是的垂直平分线,所以,
所以;
(2)因为,点是的中点,
所以平分,
因为,所以,
所以,
因为,所以,
所以,
所以,
因为,所以,
所以.
4.(1)①解:∵,是的中点;
∴处垂直平分;
连接;
∵;
∴,,三点共线;
即平分;
∵,;
∴到的距离为1.
②解:由题可知;
∵;
∴;
∴是等边三角形;
∵;
∴;
∴周长为18.
(2)解:∵;
∴;
∵垂直平分;
连接;
∴;
即;
∵;
∴;
即只需求出长即可;
∵;
∴=10;
∴周长的最小值为.
【题型4 利用三线合一证明】
1.(1)证明:连接,
∵是的中线,
∴是的中线,
∵是高,
∴,
∴,
∵是中线,
∴,
∵,
∴,
∴,
∵,
∴,
即是的中点;
(2)证明:∵,
∴,
∵,
∴,
∴,
∴.
2.(1)证明:连接,
的垂直平分线交于点,
,
,
,
为线段的中点,
;
(2)解:,
,
,
由(1)知,,
,
,,
,,
,
.
故答案为:.
3.(1)∵,
∴,
在和中,
,
∴ ;
(2),理由:
∵,
∴,
又∵平分,
∴.
4.(1)解:,,,,
,
将沿折叠,使点落在直线上的点处,
是的平分线,
,
,
在和中,
,
.
(2)解:由(1)得,,,
,
即,
,
是的平分线,
垂直平分.
【题型5 格点中画等腰三角形】
1.B
【分析】根据题意,分三种情况:当时,当时,当时,即可解答.
【详解】解:如图所示:
分三种情况:
①当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
②当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
③当时,作的垂直平分线,交网格线的格点为,,,,
综上所述:使成为等腰三角形,则满足条件的点有个,
故选:B.
2.(1)解:如图1中,即为所求(答案不唯一);
(2)解:如图2中,即为所求(答案不唯一).
3.解:如图,
……
[答案不唯一]
4.(1)解:如图:
(2)解:如图:
(3)解:如图所示:
【题型6 找出图中的等腰三角形】
1.B
【分析】本题考查了等腰三角形的判定,垂直平分线的性质,三角形的内角和,解题的关键是熟练掌握等腰三角形的判定方法,
根据两边相等的三角形即可等腰三角形即可解答
【详解】解:
,
是等腰三角形;
垂直平分线交
是等腰三角形;
,
是等腰三角形,
则图中等腰三角形的个数是3个,
故选:B
2.3
【分析】本题考查了线段垂直平分线的性质,等腰三角形的判定,熟练掌握线段垂直平分线的性质是解题的关键.
根据线段垂直平分线的性质和等腰三角形的判定可解答.
【详解】解:∵边的垂直平分线与边的垂直平分线交于点,
,
,
∴都是等腰三角形;
故答案为:3.
3.(1)解:∵,
∴,
∵,
∴,
在和中,
,
∴.
(2)解:∵由(1)可得
∴是等腰三角形,
∵,
∴,
又∵,
∴,
∴是等腰三角形.
∴图中的等腰三角形有、.
4.C
【分析】根据等腰三角形的判定,运用直角三角形的两个锐角互余和角平分线的性质,证得∠CAD=∠BAD=30°,CD=ED,AC=AE,即△ABD、△CDE、△ACE、△BCE是等腰三角形.
【详解】解:∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,
∵AD是角平分线,
∴∠CAD=∠BAD=30°,
∴AD=BD.
∴△ABD是等腰三角形.
∵AD是角平分线,∠ACB=90°,DE⊥AB,
∴CD=ED
∴AC=AE
∴△CDE、△ACE是等腰三角形;
∵AC=AE,∠BAC=60°,
∴∠ACE=60°,
∵,
∴∠BCE=30°
∴∠BCE=∠B
∴△CEB是等腰三角形
所以此图中有4个等腰三角形.
故选C.
【题型7 利用等角对等边证明等腰三角形】
1.证明:∵垂直平分,
∴,
∴,
∵,
∴,
∴;
∵,
∴,
∴为等腰三角形.
2.∵平分,
∴,
∵,,
∴,,
∵,
∴,
∴,
∴,
∴是等腰三角形.
3.证明:依题意是等边三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,,
∴,
∴.
4.(1)解:证明:在中,,,
,
平分,
,
,
,
是等腰三角形.
(2),
证明:延长至,使,连接,
,
,
,
,
,
,
平分,
,
,
,
,
,即.
【题型8 利用等角对等边求边长或证明边相等】
1.B
【分析】本题考查了角平分线的性质、平行线的性质的综合应用以及等角对等边的应用;解题的关键是熟练掌握相关性质.过E作于M,根据角平分线上的点到角两边的距离相等可求得,根据平行线和角平分线的性质易证,根据等角对等边求得,从而求得,最后根据三角形面积公式求解即可.
【详解】解:过E作于M,
平分,,,,
,
平分,
,
,
,
,
,
,
,
,
故选:B.
2.证明:∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴.
3.
【分析】本题考查了平行线的性质,等腰三角形的判定与性质,由两直线平行,内错角相等,与两个角平分线,列出相等的角,通过等角对等边,可得到两个等腰三角形,代入已知线段长度,即可求解,解题的关键是:通过平行与角平分线的条件,推导出等腰三角形.
【详解】解:,
,,
又和的平分线分别交于点、,
,,
,,
,,
,
故答案为:.
4.(1)证明:连接,如图所示:
∵,且,
∴平分,
∴,
又∵,
∴,
∴,
∴;
(2)解:在和中
,
∴,
∴,
∵,
又∵,
∴.
【题型9 尺规作等腰三角形】
1.解:如图所示,即为所求.
2.解:如图,即为所求作的等腰三角形.
3.解:①为含角的直角三角形,
①为含角的直角三角形.
4.如图,即为所求作的三角形.
已知:如图,中,.
求证:.
证明:法一:作的平分线,交于点
在和中
.
法二:取的中点为,连接.
在和中
法三:过点作于点
在和中
.
【题型10 确定与已知两点构成等腰三角形的点】
1.
【分析】点在上时,存在三种情况使为等腰三角,点在上时,存在一种情况使为等腰三角形.
【详解】解:①点在上时,
当时,
∵,,
∵,
∴,
∴,
∴;
当时,;
当时,;
②当点在上时,
存在,
综上,使为等腰三角形的点P有个,
故答案为:.
2.D
【分析】利用分类讨论的思想,当PB=PC,BP=BC,CP=BC时分别找到点P即可.
【详解】如图所示,l为长方形ABCD的对称轴,即l为AB的垂直平分线,
∴当P在l上时满足PA=PB,
作BC的中垂线交l于,满足;
作BP=BC与l交于、两点,满足,;
作CP=BC与l交于、两点,满足,;
满足题意的点P共5个,
故选:D.
3.6
【分析】本题考查了等腰三角形的判定来解决实际问题。根据题意,画出图形结合求解.
【详解】如图,第1个点在AC上,作线段的垂直平分线,交于点P,则有;
第2个点是以A为圆心,以长为半径截取,交延长线上于点P;
第3个点是以A为圆心,以长为半径截取,在上边于延长线上交于点P;
第4个点是以B为圆心,以长为半径截取,与的延长线交于点P;
第5个点是以B为圆心,以长为半径截取,与在左边交于点P;
第6个点是以A为圆心,以长为半径截取,与在右边交于点P;
故符合条件的点P有6个点.
故答案为:6.
4.C
【分析】以A为圆心,以的长为半径画弧与直线m交于点D,此时,同理以B为圆心以的长为半径画弧与直线m交于E、C,此时,,再作的垂直平分线与直线m交于点F,此时,据此可得答案.
【详解】解:如图所示,
以A为圆心,以的长为半径画弧与直线m交于点D,此时,同理以B为圆心以的长为半径画弧与直线m交于E、C,此时,,再作的垂直平分线与直线m交于点F,此时,
∴直线m上存在4个点C,使为等腰三角形,
故选:C.
【题型1 利用等边对等角求解】
1.如图,四边形中,,将沿着折叠,点B恰好落在边上的点处.若,则可表示为( )
A. B. C. D.
2.某平板电脑支架如图所示,其中,,为了使用的舒适性,可调整的大小.若增大,则的变化情况是( )
A.增大 B.减小 C.增大 D.减小
3.如图,与关于对称,,在上取一点,使得.若,则的度数是()
A. B. C. D.
4.如图,在中,,以点A为圆心,长为半径作弧交于点D,交AC于点E.再分别以点C,D为圆心,大于 长为半径作弧,两弧相交于F,G两点,作直线.若直线经过点E,则的度数为 .
【题型2 利用等边对等角进行证明】
1.如图,已知,点,,在同一条直线上.
(1)求证:;
(2)求证:;
(3)当时,求的度数.
2.如图,在中,,为边上一点,过作,分别与,相交于点和点.
(1)求证:;
(2)若,求证:.
3.如图,已知,,,,垂足为F.
(1)求证:;
(2)已知 ,求证:.
4.在中,,点D是直线上一点(不与B、C重合),以为一边在的右侧作,使,连接.
(1)如图1,当点D在线段上,且.
①证明:;
②证明:平分.
(2)如图2,当点D在直线上,设.则,之间有怎样的数量关系?请直接写出你的结论.
【题型3 利用三线合一求解】
1.如图所示,在中,,于点,,连接.
(1)若,求的度数;
(2)若点F是的中点,判断与的数量关系,并说明理由.
2.如图,在中,,点D为边的中点,连接,的平分线交于点E,已知.求和的度数.
3.如图,在中,,是边上的中线,的垂直平分线分别交、、于点、、,连接,.
(1)试说明:;
(2)若,求的度数.
4.如图,在中,,是的中点,垂直平分,交于点,交于点,是直线上的动点.
(1)当时,
①若,则点到的距离为________;
②若,,求的周长;
(2)若,且的面积为40,求周长的最小值.
【题型4 利用三线合一证明】
1.如图,在中,是边上的高线,是中线,且于,.
(1)求证:是的中点;
(2)求证.
2.如图,在中,的垂直平分线交于点,交于点,为线段的中点,.
(1)求证:;
(2)若,则的度数为 ___________.
3.如图,为线段 上一点, ,,, 平分 .
(1)求证:;
(2)问: 与 的位置关系并证明.
4.已知:如图,在中,,,于点,将沿折叠,使点A落在直线上的点处,是的平分线,交于点,交于点,连接.
(1)吗?为什么?
(2)试说明垂直平分.
【题型5 格点中画等腰三角形】
1.如图,在的网格中,每个网格线的交点称为格点.已知图中,两个格点,请在图中再寻找另一个格点,使成为等腰三角形,则满足条件的点有( )个.
A. B. C. D.
2.在方格纸中,点P、Q都在格点上,请用无刻度的直尺按要求画格点三角形:
(1)在图1中,画一个以为腰的等腰(为格点);
(2)在图2中,画一个以为底的等腰(为格点).
3.如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个等腰,且使得点为格点.请在下面的网格图中画出3种不同的等腰.
4.图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图1、图2、图3给定的网格中按要求作图.
要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
(1)在图1中的格点上确定一点P,画一个以AB为腰的等腰△ABP.
(2)在图2中的格点上确定一点P,画一个以AB为底的等腰△ABP.
(3)在图3中的格线MN上确定一点P,使PA与PB的长度之和最小.
【题型6 找出图中的等腰三角形】
1.如图,在中,,的垂直平分线交于点D、E,则图中等腰三角形的个数是( )
A.2 B.3 C.4 D.5
2.如图,在中,已知边的垂直平分线与边的垂直平分线交于点,连接,则图中有 个等腰三角形.
3.如图,在四边形中,,,,点E是线段上一点,且.
(1)求证:;
(2)直接写出图中所有的等腰三角形.
4.如图,中,,,平分,于点,连结交于点,则图中的等腰三角形有( )
A.2个 B.3个 C.4个 D.5个
【题型7 利用等角对等边证明等腰三角形】
1.如图,在中,,,边的垂直平分线与交于点,与交于点,连接.求证:是等腰三角形.
2.如图,在中,,是斜边上的高,角平分线交于点.求证:是等腰三角形.
3.如图,,点分别在,上,以,为边在内作等边三角形,,连接并延长交于点,求证:.
4.如图,在中,,,与的角平分线、分别交、边于点D和点E.
(1)求证:是等腰三角形;
(2)用等式表示线段之间的数量关系,并证明.
【题型8 利用等角对等边求边长或证明边相等】
1.如图,在中,,分别是和的平分线,,交于点D,于点F.若,,,则的面积为( )
A.50 B.55 C.60 D.65
2.如图,,,交于F,交于点E,求证:.
3.如图,在中,,和的平分线分别交于点、,若,,,,则 .
4.已知:如图,点D是的边上的一点,过点D作,,垂足分别为E、F,再过点D作,交于点G,且.
求证:
(1);
(2).
【题型9 尺规作等腰三角形】
1.如图,已知一个等腰三角形的底边为c,底边上的高为,求作这个等腰三角形.(保留作图痕迹,不必写作法)
2.如图,已知,点B是射线上一点,求作等腰三角形,使得为等腰三角形的底边,点A在内部,且点A到角的两边距离相等.(尺规作图)
3.如图.已知一个含有角的直角三角形,请利用它用两种不同的方法构造一个含角的直角三角形.(尺规作图,不写做法,保留作图轨迹)
4.证明:等腰三角形的两底角相等.要求:
(1)用无刻度的直尺和圆规作等腰,使底边,腰;
(2)结合图形,写出已知、求证,并完成证明;
(3)证明过程若需添加辅助线,则辅助线也需用无刻度的直尺和圆规作图.
【题型10 确定与已知两点构成等腰三角形的点】
1.如图所示,在中,,,点D在CA上,且,动点P从A点出发沿A→B→C的路线运动,运动到点C停止.在点P的运动过程中,使为等腰三角形的点P有 个.
2.如图所示,在长方形的对称轴上找点,使得、均为等腰三角形,则满足条件的点的个数是( )
A.2 B.3 C.4 D.5
3.如图,已知中,.在直线或上取一点P,使得是等腰三角形,则符合条件的P点有 个.
4.如图,线段的一个端点B在直线m上,直线m上存在点C,使为等腰三角形,这样的点C有( )
A.2个 B.3个 C.4个 D.5个
参考答案
【题型1 利用等边对等角求解】
1.B
【分析】本题考查了折叠的性质,等腰三角形的性质,三角形外角的性质;由折叠得,,由等腰三角形的性质得,由三角形外角的性质得 ,即可求解;掌握折叠的性质,等腰三角形的性质是解题的关键.
【详解】解:由折叠得:
,
,
,
,
,
,
,
,
,
,
故选:B.
2.D
【分析】本题考查了等腰三角形的性质,三角形内角和定理等知识,设设原来,求出此时,然后类似求出变化后,然后两角作差即可得出结论.
【详解】解:设原来,则
∵,
∴,
∴,
增大后,,
∴,
∴,
∴,
∴的变化情况是减小,
故选:D.
3.A
【分析】本题考查了轴对称性质、等腰三角形的性质及直角三角形的性质,解决本题的关键是熟练掌握轴对称性质、等腰三角形的性质及直角三角形的性质,由轴对称性质得,
设,得出,再由等腰三角形的性质得.再由直角三角形的性质列出方程求解即可.
【详解】解:与关于对称,
,
设.
,
在中,,
.
又,
,
,
故选:A
4.
【分析】本题考查了作图复杂作图,线段垂直平分线的性质和等腰三角形的性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作. 连接、,如图,设,利用基本作图得到,则,所以,再根据等腰三角形的性质和三角形内角和得到,接着利用得到,则根据求出.
【详解】解:连接、,如图,设,
由作法得垂直平分,
,
,
,
,,
,
,,
,,
,
,
解得,
.
故答案为:.
【题型2 利用等边对等角进行证明】
1.(1)证明:,
,
即,
在和中,
,
;
(2)证明:,
,
,
,
,
,
;
(3)解:,
,
,
,
,
.
2.(1)∵,
∴,
又∵,,
∴;
(2)在和中
,
∴,
∴.
3.(1)∵,
∴,,
∴,
在和中,
,
∴.
(2)如图,延长到G,使,连接,
∵,
∴,
∴,
∵,
∴,
由(1)得:,
,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴.
4.(1)证明:① ,
,
,
在和中,
,
;
② 中,,
,
由①得,
,
,
平分.
(2)解:,
①点D在线段上,如图:
,
,
,
在和中,
,
;
,
在中,,
∴,
∴,
∵,
∴;
②当点D在射线上时,如图:
,
,
,
在和中,
,
,
,
在中,,
∴,
∴,
∵,
∴;
③当点D在射线上时,如图:
同理可得 ,
∴,
在中,,
∴,
∴.
∵,
∴;
综上所述α,β之间的数量关系为:或.
【题型3 利用三线合一求解】
1.(1)解:∵,
∴,
∵,,
∴,
在Rt△FDC中,
∴,
∵,
∴,
∴,
∵,
∴;
(2),理由如下:
∵,且点F是的中点,
∴,,
∴,,
∴,
∴.
2.解:∵,点D为边的中点,
∴,,
∴,
∵,,
∴,
∵是的平分线,
∴,
在中,
,
∴.
3.(1)因为,点是的中点,
所以,所以是的垂直平分线,
所以,
因为是的垂直平分线,所以,
所以;
(2)因为,点是的中点,
所以平分,
因为,所以,
所以,
因为,所以,
所以,
所以,
因为,所以,
所以.
4.(1)①解:∵,是的中点;
∴处垂直平分;
连接;
∵;
∴,,三点共线;
即平分;
∵,;
∴到的距离为1.
②解:由题可知;
∵;
∴;
∴是等边三角形;
∵;
∴;
∴周长为18.
(2)解:∵;
∴;
∵垂直平分;
连接;
∴;
即;
∵;
∴;
即只需求出长即可;
∵;
∴=10;
∴周长的最小值为.
【题型4 利用三线合一证明】
1.(1)证明:连接,
∵是的中线,
∴是的中线,
∵是高,
∴,
∴,
∵是中线,
∴,
∵,
∴,
∴,
∵,
∴,
即是的中点;
(2)证明:∵,
∴,
∵,
∴,
∴,
∴.
2.(1)证明:连接,
的垂直平分线交于点,
,
,
,
为线段的中点,
;
(2)解:,
,
,
由(1)知,,
,
,,
,,
,
.
故答案为:.
3.(1)∵,
∴,
在和中,
,
∴ ;
(2),理由:
∵,
∴,
又∵平分,
∴.
4.(1)解:,,,,
,
将沿折叠,使点落在直线上的点处,
是的平分线,
,
,
在和中,
,
.
(2)解:由(1)得,,,
,
即,
,
是的平分线,
垂直平分.
【题型5 格点中画等腰三角形】
1.B
【分析】根据题意,分三种情况:当时,当时,当时,即可解答.
【详解】解:如图所示:
分三种情况:
①当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
②当时,以点为圆心,以长为半径作圆,交网格线的格点为,,
③当时,作的垂直平分线,交网格线的格点为,,,,
综上所述:使成为等腰三角形,则满足条件的点有个,
故选:B.
2.(1)解:如图1中,即为所求(答案不唯一);
(2)解:如图2中,即为所求(答案不唯一).
3.解:如图,
……
[答案不唯一]
4.(1)解:如图:
(2)解:如图:
(3)解:如图所示:
【题型6 找出图中的等腰三角形】
1.B
【分析】本题考查了等腰三角形的判定,垂直平分线的性质,三角形的内角和,解题的关键是熟练掌握等腰三角形的判定方法,
根据两边相等的三角形即可等腰三角形即可解答
【详解】解:
,
是等腰三角形;
垂直平分线交
是等腰三角形;
,
是等腰三角形,
则图中等腰三角形的个数是3个,
故选:B
2.3
【分析】本题考查了线段垂直平分线的性质,等腰三角形的判定,熟练掌握线段垂直平分线的性质是解题的关键.
根据线段垂直平分线的性质和等腰三角形的判定可解答.
【详解】解:∵边的垂直平分线与边的垂直平分线交于点,
,
,
∴都是等腰三角形;
故答案为:3.
3.(1)解:∵,
∴,
∵,
∴,
在和中,
,
∴.
(2)解:∵由(1)可得
∴是等腰三角形,
∵,
∴,
又∵,
∴,
∴是等腰三角形.
∴图中的等腰三角形有、.
4.C
【分析】根据等腰三角形的判定,运用直角三角形的两个锐角互余和角平分线的性质,证得∠CAD=∠BAD=30°,CD=ED,AC=AE,即△ABD、△CDE、△ACE、△BCE是等腰三角形.
【详解】解:∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,
∵AD是角平分线,
∴∠CAD=∠BAD=30°,
∴AD=BD.
∴△ABD是等腰三角形.
∵AD是角平分线,∠ACB=90°,DE⊥AB,
∴CD=ED
∴AC=AE
∴△CDE、△ACE是等腰三角形;
∵AC=AE,∠BAC=60°,
∴∠ACE=60°,
∵,
∴∠BCE=30°
∴∠BCE=∠B
∴△CEB是等腰三角形
所以此图中有4个等腰三角形.
故选C.
【题型7 利用等角对等边证明等腰三角形】
1.证明:∵垂直平分,
∴,
∴,
∵,
∴,
∴;
∵,
∴,
∴为等腰三角形.
2.∵平分,
∴,
∵,,
∴,,
∵,
∴,
∴,
∴,
∴是等腰三角形.
3.证明:依题意是等边三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,,
∴,
∴.
4.(1)解:证明:在中,,,
,
平分,
,
,
,
是等腰三角形.
(2),
证明:延长至,使,连接,
,
,
,
,
,
,
平分,
,
,
,
,
,即.
【题型8 利用等角对等边求边长或证明边相等】
1.B
【分析】本题考查了角平分线的性质、平行线的性质的综合应用以及等角对等边的应用;解题的关键是熟练掌握相关性质.过E作于M,根据角平分线上的点到角两边的距离相等可求得,根据平行线和角平分线的性质易证,根据等角对等边求得,从而求得,最后根据三角形面积公式求解即可.
【详解】解:过E作于M,
平分,,,,
,
平分,
,
,
,
,
,
,
,
,
故选:B.
2.证明:∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴.
3.
【分析】本题考查了平行线的性质,等腰三角形的判定与性质,由两直线平行,内错角相等,与两个角平分线,列出相等的角,通过等角对等边,可得到两个等腰三角形,代入已知线段长度,即可求解,解题的关键是:通过平行与角平分线的条件,推导出等腰三角形.
【详解】解:,
,,
又和的平分线分别交于点、,
,,
,,
,,
,
故答案为:.
4.(1)证明:连接,如图所示:
∵,且,
∴平分,
∴,
又∵,
∴,
∴,
∴;
(2)解:在和中
,
∴,
∴,
∵,
又∵,
∴.
【题型9 尺规作等腰三角形】
1.解:如图所示,即为所求.
2.解:如图,即为所求作的等腰三角形.
3.解:①为含角的直角三角形,
①为含角的直角三角形.
4.如图,即为所求作的三角形.
已知:如图,中,.
求证:.
证明:法一:作的平分线,交于点
在和中
.
法二:取的中点为,连接.
在和中
法三:过点作于点
在和中
.
【题型10 确定与已知两点构成等腰三角形的点】
1.
【分析】点在上时,存在三种情况使为等腰三角,点在上时,存在一种情况使为等腰三角形.
【详解】解:①点在上时,
当时,
∵,,
∵,
∴,
∴,
∴;
当时,;
当时,;
②当点在上时,
存在,
综上,使为等腰三角形的点P有个,
故答案为:.
2.D
【分析】利用分类讨论的思想,当PB=PC,BP=BC,CP=BC时分别找到点P即可.
【详解】如图所示,l为长方形ABCD的对称轴,即l为AB的垂直平分线,
∴当P在l上时满足PA=PB,
作BC的中垂线交l于,满足;
作BP=BC与l交于、两点,满足,;
作CP=BC与l交于、两点,满足,;
满足题意的点P共5个,
故选:D.
3.6
【分析】本题考查了等腰三角形的判定来解决实际问题。根据题意,画出图形结合求解.
【详解】如图,第1个点在AC上,作线段的垂直平分线,交于点P,则有;
第2个点是以A为圆心,以长为半径截取,交延长线上于点P;
第3个点是以A为圆心,以长为半径截取,在上边于延长线上交于点P;
第4个点是以B为圆心,以长为半径截取,与的延长线交于点P;
第5个点是以B为圆心,以长为半径截取,与在左边交于点P;
第6个点是以A为圆心,以长为半径截取,与在右边交于点P;
故符合条件的点P有6个点.
故答案为:6.
4.C
【分析】以A为圆心,以的长为半径画弧与直线m交于点D,此时,同理以B为圆心以的长为半径画弧与直线m交于E、C,此时,,再作的垂直平分线与直线m交于点F,此时,据此可得答案.
【详解】解:如图所示,
以A为圆心,以的长为半径画弧与直线m交于点D,此时,同理以B为圆心以的长为半径画弧与直线m交于E、C,此时,,再作的垂直平分线与直线m交于点F,此时,
∴直线m上存在4个点C,使为等腰三角形,
故选:C.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
