第9章矩形的判定证明题专项训练(含解析)
文档属性
| 名称 | 第9章矩形的判定证明题专项训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 07:14:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第9章矩形的判定证明题专项训练-2024-2025学年数学八年级下册苏科版
1.如图,在中,于点,延长至点,使,连接与DE交于点.
(1)求证:四边形为矩形;
(2)若,求的长.
2.如图,在中,,是的角平分线,四边形是平行四边形.求证:四边形是矩形.
3.如图,在四边形中,,和互相平分并交于点,,求证:四边形是矩形.
4.如图,在四边形中,,,,,若动点从点出发,以的速度沿线段向点运动;动点从点出发,以的速度沿向点运动,当点到达点时,动点,同时停止运动.已知点,同时出发,运动时间为.
(1)当取何值时,四边形为平行四边形?
(2)当取何值时,四边形为矩形?
5.已知:如图,E是外一点,且.
求证:四边形是矩形.
6.如图,在中,点分别在边上,且.
(1)求证:;
下面是小轩的证明过程:
证明:四边形是平行四边形,
.①
,
,②
在与中,
,
;
上述推理过程从第___________步开始出现错误?请写出完整的正确证明过程.
(2)请添加一个条件___________,使四边形是矩形.(直接填空,不需说明理由)
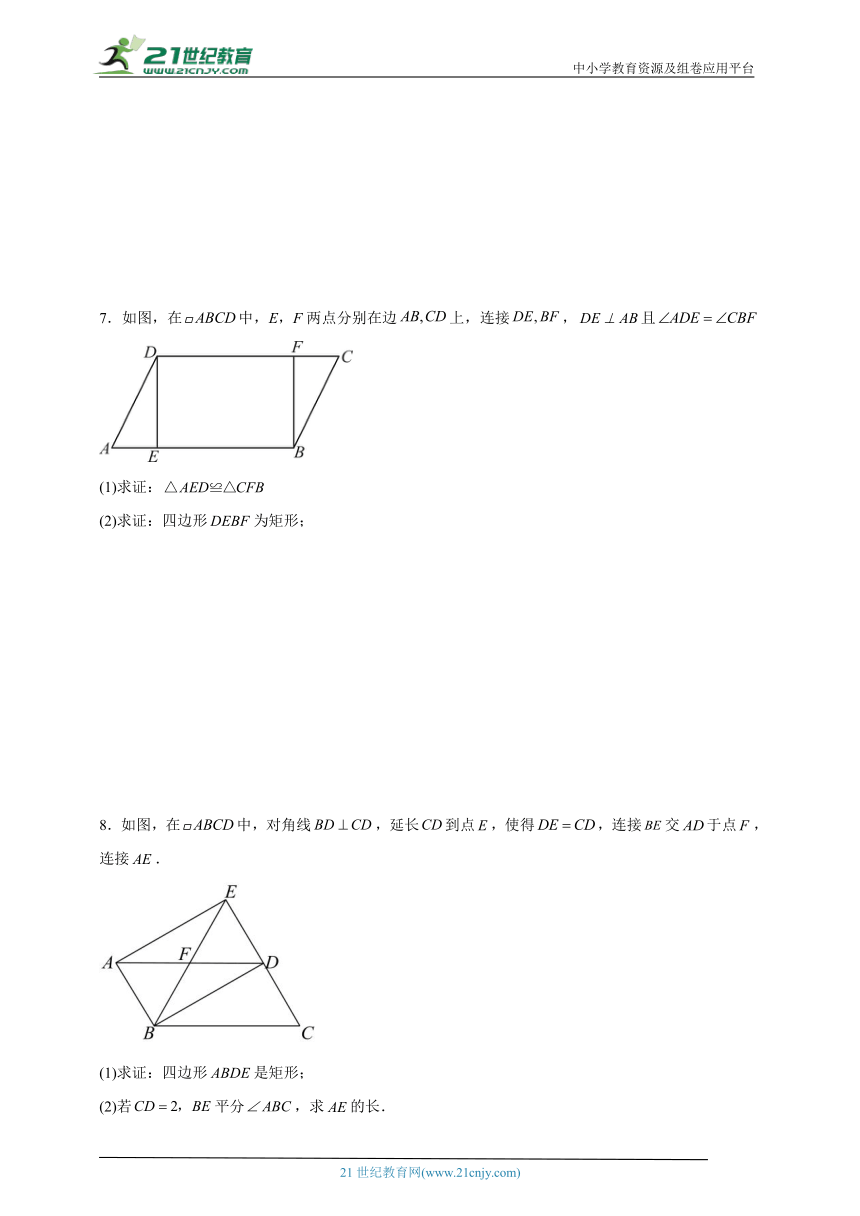
7.如图,在中,E,F两点分别在边上,连接,且
(1)求证:
(2)求证:四边形为矩形;
8.如图,在中,对角线,延长到点,使得,连接交于点,连接.
(1)求证:四边形是矩形;
(2)若平分,求的长.
9.已知:如图,在中,,,垂足为,是外角的平分线,,垂足为,连接交于.
(1)求证:四边形为矩形.
(2)①判断四边形的形状,并证明你的结论.
②线段与有怎样的关系?直接写出你的结论.
10.如图,在四边形中,,,.
(1)求证:四边形是矩形;
(2)点是上一点,点是的中点,连接,,,若,,,求的长.
11.如图,的对角线,相交于点,将对角线向两个方向延长,分别至点和点,且使.
(1)求证:;
(2)若,求证:四边形是矩形.
12.如图,已知点是平行四边形中边的中点,连接并延长交的延长线于点,连接,且.求证:四边形为矩形.
13.已知:如图,在菱形中,对角线相交于点O,过点D作,且,连接.
(1)求证:四边形是矩形;
(2)若,求的长.
14.如图,在中,是上一点(不与点,重合),,过点作,交于点,连接,.
(1)求证:四边形是矩形;
(2)当,时,求和的长.
15.如图,已知为等边三角形,,点为线段上任意一点(点不与、重合),过点作,分别交、于、.
(1)求证:;
(2)试探索:当为的中点时,四边形是什么样的特殊四边形?并说明理由.
《第9章矩形的判定证明题专项训练-2024-2025学年数学八年级下册苏科版》参考答案
1.(1)见解析
(2)
【分析】本题考查平行四边形的判定和性质,矩形的判定和性质,勾股定理及其逆定理等知识点,熟练掌握相关知识点,是解题的关键:
(1)先证明四边形为平行四边形,再根据有一个角为直角的平行四边形是矩形,即可得证;
(2)矩形的性质,得到,勾股定理逆定理,得到,等积法求出的长,再利用勾股定理求出的长即可.
【详解】(1)证明:∵四边形是平行四边形,
∴,
∴,
∵,
∴,即:,
∴,
∴四边形为平行四边形,
∵,
∴,
∴平行四边形为矩形;
(2)由(1)知:四边形为矩形,
∴,
∵,
∴,
∴,
∵,
∴,即:,
∴,
在中,由勾股定理,得:,
∴.
2.证明见解析
【分析】本题考查矩形的判定,平行四边形的判定与性质,等腰三角形的三线合一,熟练掌握这些性质与判定是解题的关键.先利用三线合一得出,,利用四边形是平行四边形结合,推出四边形是平行四边形,再结合,即可证明.
【详解】证明:∵,是的角平分线,
∴,,
∵四边形是平行四边形,
∴,,
∴,,
∴四边形是平行四边形,
∵,
∴四边形是矩形.
3.见解析
【分析】本题考查了矩形的判定,平行四边形的判定与性质,连接,根据对角线互相平分的四边形是平行四边形判断出四边形是平行四边形,根据平行四边形的对边平行且相等可得,,然后求出,再求出四边形是平行四边形,然后根据有一个角是直角的平行四边形是矩形证明.
【详解】证明:如图,连接,
∵和互相平分,
∴四边形是平行四边形,
∴,
∵,
∴,
即,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形.
4.(1)
(2)
【分析】本题考查了矩形的判定、平行四边形的判定等知识,此题难度适中,注意掌握数形结合思想与方程思想的应用.
(1)当时,四边形为平行四边形,根据列出关于t的方程,解方程即可;
(2)当时,四边形为矩形,根据列出关于t的方程,解方程即可.
【详解】(1)解:如图,,
当时,四边形为平行四边形.
根据题意,,,
,
解得,
当时,四边形为平行四边形.
(2)解:如图,,,
当时,四边形为矩形.
根据题意,,,
,
解得,
当时,四边形为矩形.
5.见解析
【分析】本题考查平行四边形的性质,斜边上的中线,矩形的判定,熟练掌握相关知识点,是解题的关键:
连接、,设、相交于点,连接,根据斜边上的中线得到,,进而得到,即可得证.
【详解】证明:连接、,设、相交于点,连接,则:,
在中,是斜边的中点,
所以.
同理,在中,,
,
,即,
是矩形.
6.(1)②,证明过程见解析
(2)(答案不唯一)
【分析】本题主要考查了平行四边形的性质,全等三角形的判定,矩形的判定,
对于(1),根据平行四边形的性质得,再根据可得,然后根据“边角边”得出答案;
对于(2),先证明四边形是平行四边形,再根据有一个角是直角的平行四边形是矩形得出答案.
【详解】(1)解:上述推理过程从第②步开始出现错误.
证明:∵四边形是平行四边形,
∴.
∵,
∴.
在和中,
,
∴;
故答案为:②;
(2)解:.(答案不唯一)
∵,,
∴四边形是平行四边形.
当时,
∴四边形是矩形.
故答案为:.(答案不唯一)
7.(1)见解析
(2)见解析
【分析】本题考查了矩形的性质与判定、平行四边形的性质,全等三角形的性质与判定,熟练掌握相关知识点是解题的关键.
(1)利用平行四边形的性质得到,,,由得到,进而得到,即可证明;
(2)由得到,最后利用矩形的判定即可证明.
【详解】(1)证明:,
,,,
,
,
又,
,
在和中,
,
;
(2)证明:,
,
,
,
四边形为矩形.
8.(1)证明见解析;
(2).
【分析】本题主要考查了平行四边形的判定与性质,矩形的判定与性质,勾股定理,掌握知识点的应用是解题的关键是.
()由平行四边形的性质得出,,再由得出,从而证明四边形是平行四边形,然后根据矩形的判定方法即可求证;
()由()得:四边形是矩形,则,,再由平行线的性质及等腰三角形的判定得出,然后由勾股定理即可求解.
【详解】(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形;
(2)解:由()得:四边形是矩形,
∴,,
∴,
∵平分,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴.
9.(1)见解析
(2)①四边形是平行四边形,见解析;②,,理由见解析
【分析】本题主要考查了矩形的判定与性质,等腰三角形的性质,平行四边形的判定与性质,角平分线的定义,熟练掌握平行四边形和矩形的各种判定方法是解题关键.
(1)根据,,得,根据等腰三角形的三线合一,得,根据角平分线的定义,得,推出,即可证明四边形为矩形;
(2)①根据四边形为矩形,得,,根据等腰三角形三线合一,得,推出,即可证明;②根据四边形为矩形,得,根据四边形是平行四边形,得,,即可求解.
【详解】(1)证明:∵在中,,,,
∴,平分,
∴,
∵是外角的平分线,
∴,
∴,
∴,
∴四边形为矩形.
(2)解:①四边形是平行四边形,理由如下:
∵四边形为矩形,
∴,,
∵,,
∴,
∴,
∴四边形是平行四边形;
②,,理由如下:
∵四边形为矩形,
∴,
∵四边形是平行四边形,
∴,,
∴,.
10.(1)见解析
(2)
【分析】本题主要考查了矩形的判定,勾股定理的逆定理,直角三角形斜边上的中线性质,熟练掌握矩形的判定方法是解题关键.
(1)根据有一个角是直角的平行四边形是矩形即可求解;
(2)根据勾股定理的逆定理证明是直角三角形,进而根据直角三角形斜边上的中线性质可知,即可求解.
【详解】(1)证明:∵,,
∴四边形是平行四边形.
∵,
∴四边形是矩形.
(2)解:∵,,,
∴,
∴是直角三角形,且,
∵点是的中点,
∴.
11.(1)见解析
(2)见解析
【分析】此题考查了平行四边形的判定和性质,全等三角形的判定和性质,矩形的判定,熟练掌握矩形的判定是解题的关键,解题时要注意选择适宜的判定方法.
(1)由四边形是平行四边形易知,,即可得出结论;
(2)证明四边形为平行四边形,由平行四边形的性质证出,根据矩形的判定可得出结论.
【详解】(1)证明:四边形为平行四边形,
,,
,
,即,
在与中,
,
(2)证明:,
,
,
四边形为平行四边形,
,
,
,即,
平行四边形为矩形.
12.见解析
【分析】该题考查了平行四边形的性质,矩形的判定,全等三角形的性质和判定,根据平行四边形的性质得到两角一边对应相等,利用判定,从而得到,结合已知可得四边形是平行四边形,结合,根据对角线相等的平行四边形是矩形,可得到四边形是矩形.
【详解】证明:∵四边形是平行四边形,
∴,
∴,,
又∵为中点,
∴,
∴,
∴,
∴四边形是平行四边形,
又∵,
∴四边形是矩形.
13.(1)见解析
(2)
【分析】(1)由菱形的性质得,再根据平行四边形的判定定理(一组对边平行且相等的四边形是平行四边形)证明四边形是平行四边形,然后由矩形的定义(有一个角是直角的平行四边形叫做矩形)即可得出结论;
(2)由矩形的性质得,再根据菱形的性质可知,;在中,根据勾股定理可得的长,即可得到答案.
【详解】(1)证明:∵四边形是菱形
∴
∵
∴
∴四边形是平行四边形
又∵
∴
∴四边形是矩形
(2)解:∵四边形是矩形,
∴
∵四边形是菱形,
∴,
∴在中,根据勾股定理可得
∴
【点睛】本题考查了矩形的判定与性质、菱形的性质、平行四边形的判定及勾股定理,熟练掌握矩形的判定与性质是解题的关键.
14.(1)见解析
(2),
【分析】(1)根据题意证明出,即可得证;
(2)根据已知条件和矩形的性质证明,得到,设,则,在中,由勾股定理得:,
即,解出的值即可求出的长,设,则,在中,根据勾股定理得:,即,解出的值即可求出的长.
【详解】(1)证明:,,
,
,
,
四边形是矩形;
(2)解:四边形是矩形,
,
在和中,
,
,
,
设,则,
在中,由勾股定理得:,
,
解得:,
,
设,则,
在中,根据勾股定理得:,
即,
解得:,
.
【点睛】本题考查了外角的定义,矩形的判定与性质,直角三角形全等的判定,勾股定理,熟练掌握以上知识点是解答本题的关键.
15.(1)见解析;
(2)当为的中点时,四边形是矩形,理由见解析.
【分析】此题考查矩形的判定,全等三角形的判定与性质,等边三角形的性质和平行四边形的判定,解题关键在于根据已知条件两组对边相互平行证明平行四边形.
(1)证出,再加上条件,可得,可得到;
(2)首先证明四边形是平行四边形,再证明,即可以证出四边形是矩形.
【详解】(1)证明:如图,
∵是等边三角形,
∴,,
∵,
∴,
∴,
∵(即),,
∴四边形是平行四边形;
∴,
在和中,
,
∴,
∴;
(2)解:当为的中点时,四边形是矩形,
理由:∵为的中点,
∴,
又由()证得:,
∴,
∵,即,
∴四边形是平行四边形
又∵是等边三角形,为的中点,
∴(三线合一),
∴,
∴四边形是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第9章矩形的判定证明题专项训练-2024-2025学年数学八年级下册苏科版
1.如图,在中,于点,延长至点,使,连接与DE交于点.
(1)求证:四边形为矩形;
(2)若,求的长.
2.如图,在中,,是的角平分线,四边形是平行四边形.求证:四边形是矩形.
3.如图,在四边形中,,和互相平分并交于点,,求证:四边形是矩形.
4.如图,在四边形中,,,,,若动点从点出发,以的速度沿线段向点运动;动点从点出发,以的速度沿向点运动,当点到达点时,动点,同时停止运动.已知点,同时出发,运动时间为.
(1)当取何值时,四边形为平行四边形?
(2)当取何值时,四边形为矩形?
5.已知:如图,E是外一点,且.
求证:四边形是矩形.
6.如图,在中,点分别在边上,且.
(1)求证:;
下面是小轩的证明过程:
证明:四边形是平行四边形,
.①
,
,②
在与中,
,
;
上述推理过程从第___________步开始出现错误?请写出完整的正确证明过程.
(2)请添加一个条件___________,使四边形是矩形.(直接填空,不需说明理由)
7.如图,在中,E,F两点分别在边上,连接,且
(1)求证:
(2)求证:四边形为矩形;
8.如图,在中,对角线,延长到点,使得,连接交于点,连接.
(1)求证:四边形是矩形;
(2)若平分,求的长.
9.已知:如图,在中,,,垂足为,是外角的平分线,,垂足为,连接交于.
(1)求证:四边形为矩形.
(2)①判断四边形的形状,并证明你的结论.
②线段与有怎样的关系?直接写出你的结论.
10.如图,在四边形中,,,.
(1)求证:四边形是矩形;
(2)点是上一点,点是的中点,连接,,,若,,,求的长.
11.如图,的对角线,相交于点,将对角线向两个方向延长,分别至点和点,且使.
(1)求证:;
(2)若,求证:四边形是矩形.
12.如图,已知点是平行四边形中边的中点,连接并延长交的延长线于点,连接,且.求证:四边形为矩形.
13.已知:如图,在菱形中,对角线相交于点O,过点D作,且,连接.
(1)求证:四边形是矩形;
(2)若,求的长.
14.如图,在中,是上一点(不与点,重合),,过点作,交于点,连接,.
(1)求证:四边形是矩形;
(2)当,时,求和的长.
15.如图,已知为等边三角形,,点为线段上任意一点(点不与、重合),过点作,分别交、于、.
(1)求证:;
(2)试探索:当为的中点时,四边形是什么样的特殊四边形?并说明理由.
《第9章矩形的判定证明题专项训练-2024-2025学年数学八年级下册苏科版》参考答案
1.(1)见解析
(2)
【分析】本题考查平行四边形的判定和性质,矩形的判定和性质,勾股定理及其逆定理等知识点,熟练掌握相关知识点,是解题的关键:
(1)先证明四边形为平行四边形,再根据有一个角为直角的平行四边形是矩形,即可得证;
(2)矩形的性质,得到,勾股定理逆定理,得到,等积法求出的长,再利用勾股定理求出的长即可.
【详解】(1)证明:∵四边形是平行四边形,
∴,
∴,
∵,
∴,即:,
∴,
∴四边形为平行四边形,
∵,
∴,
∴平行四边形为矩形;
(2)由(1)知:四边形为矩形,
∴,
∵,
∴,
∴,
∵,
∴,即:,
∴,
在中,由勾股定理,得:,
∴.
2.证明见解析
【分析】本题考查矩形的判定,平行四边形的判定与性质,等腰三角形的三线合一,熟练掌握这些性质与判定是解题的关键.先利用三线合一得出,,利用四边形是平行四边形结合,推出四边形是平行四边形,再结合,即可证明.
【详解】证明:∵,是的角平分线,
∴,,
∵四边形是平行四边形,
∴,,
∴,,
∴四边形是平行四边形,
∵,
∴四边形是矩形.
3.见解析
【分析】本题考查了矩形的判定,平行四边形的判定与性质,连接,根据对角线互相平分的四边形是平行四边形判断出四边形是平行四边形,根据平行四边形的对边平行且相等可得,,然后求出,再求出四边形是平行四边形,然后根据有一个角是直角的平行四边形是矩形证明.
【详解】证明:如图,连接,
∵和互相平分,
∴四边形是平行四边形,
∴,
∵,
∴,
即,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形.
4.(1)
(2)
【分析】本题考查了矩形的判定、平行四边形的判定等知识,此题难度适中,注意掌握数形结合思想与方程思想的应用.
(1)当时,四边形为平行四边形,根据列出关于t的方程,解方程即可;
(2)当时,四边形为矩形,根据列出关于t的方程,解方程即可.
【详解】(1)解:如图,,
当时,四边形为平行四边形.
根据题意,,,
,
解得,
当时,四边形为平行四边形.
(2)解:如图,,,
当时,四边形为矩形.
根据题意,,,
,
解得,
当时,四边形为矩形.
5.见解析
【分析】本题考查平行四边形的性质,斜边上的中线,矩形的判定,熟练掌握相关知识点,是解题的关键:
连接、,设、相交于点,连接,根据斜边上的中线得到,,进而得到,即可得证.
【详解】证明:连接、,设、相交于点,连接,则:,
在中,是斜边的中点,
所以.
同理,在中,,
,
,即,
是矩形.
6.(1)②,证明过程见解析
(2)(答案不唯一)
【分析】本题主要考查了平行四边形的性质,全等三角形的判定,矩形的判定,
对于(1),根据平行四边形的性质得,再根据可得,然后根据“边角边”得出答案;
对于(2),先证明四边形是平行四边形,再根据有一个角是直角的平行四边形是矩形得出答案.
【详解】(1)解:上述推理过程从第②步开始出现错误.
证明:∵四边形是平行四边形,
∴.
∵,
∴.
在和中,
,
∴;
故答案为:②;
(2)解:.(答案不唯一)
∵,,
∴四边形是平行四边形.
当时,
∴四边形是矩形.
故答案为:.(答案不唯一)
7.(1)见解析
(2)见解析
【分析】本题考查了矩形的性质与判定、平行四边形的性质,全等三角形的性质与判定,熟练掌握相关知识点是解题的关键.
(1)利用平行四边形的性质得到,,,由得到,进而得到,即可证明;
(2)由得到,最后利用矩形的判定即可证明.
【详解】(1)证明:,
,,,
,
,
又,
,
在和中,
,
;
(2)证明:,
,
,
,
四边形为矩形.
8.(1)证明见解析;
(2).
【分析】本题主要考查了平行四边形的判定与性质,矩形的判定与性质,勾股定理,掌握知识点的应用是解题的关键是.
()由平行四边形的性质得出,,再由得出,从而证明四边形是平行四边形,然后根据矩形的判定方法即可求证;
()由()得:四边形是矩形,则,,再由平行线的性质及等腰三角形的判定得出,然后由勾股定理即可求解.
【详解】(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形;
(2)解:由()得:四边形是矩形,
∴,,
∴,
∵平分,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴.
9.(1)见解析
(2)①四边形是平行四边形,见解析;②,,理由见解析
【分析】本题主要考查了矩形的判定与性质,等腰三角形的性质,平行四边形的判定与性质,角平分线的定义,熟练掌握平行四边形和矩形的各种判定方法是解题关键.
(1)根据,,得,根据等腰三角形的三线合一,得,根据角平分线的定义,得,推出,即可证明四边形为矩形;
(2)①根据四边形为矩形,得,,根据等腰三角形三线合一,得,推出,即可证明;②根据四边形为矩形,得,根据四边形是平行四边形,得,,即可求解.
【详解】(1)证明:∵在中,,,,
∴,平分,
∴,
∵是外角的平分线,
∴,
∴,
∴,
∴四边形为矩形.
(2)解:①四边形是平行四边形,理由如下:
∵四边形为矩形,
∴,,
∵,,
∴,
∴,
∴四边形是平行四边形;
②,,理由如下:
∵四边形为矩形,
∴,
∵四边形是平行四边形,
∴,,
∴,.
10.(1)见解析
(2)
【分析】本题主要考查了矩形的判定,勾股定理的逆定理,直角三角形斜边上的中线性质,熟练掌握矩形的判定方法是解题关键.
(1)根据有一个角是直角的平行四边形是矩形即可求解;
(2)根据勾股定理的逆定理证明是直角三角形,进而根据直角三角形斜边上的中线性质可知,即可求解.
【详解】(1)证明:∵,,
∴四边形是平行四边形.
∵,
∴四边形是矩形.
(2)解:∵,,,
∴,
∴是直角三角形,且,
∵点是的中点,
∴.
11.(1)见解析
(2)见解析
【分析】此题考查了平行四边形的判定和性质,全等三角形的判定和性质,矩形的判定,熟练掌握矩形的判定是解题的关键,解题时要注意选择适宜的判定方法.
(1)由四边形是平行四边形易知,,即可得出结论;
(2)证明四边形为平行四边形,由平行四边形的性质证出,根据矩形的判定可得出结论.
【详解】(1)证明:四边形为平行四边形,
,,
,
,即,
在与中,
,
(2)证明:,
,
,
四边形为平行四边形,
,
,
,即,
平行四边形为矩形.
12.见解析
【分析】该题考查了平行四边形的性质,矩形的判定,全等三角形的性质和判定,根据平行四边形的性质得到两角一边对应相等,利用判定,从而得到,结合已知可得四边形是平行四边形,结合,根据对角线相等的平行四边形是矩形,可得到四边形是矩形.
【详解】证明:∵四边形是平行四边形,
∴,
∴,,
又∵为中点,
∴,
∴,
∴,
∴四边形是平行四边形,
又∵,
∴四边形是矩形.
13.(1)见解析
(2)
【分析】(1)由菱形的性质得,再根据平行四边形的判定定理(一组对边平行且相等的四边形是平行四边形)证明四边形是平行四边形,然后由矩形的定义(有一个角是直角的平行四边形叫做矩形)即可得出结论;
(2)由矩形的性质得,再根据菱形的性质可知,;在中,根据勾股定理可得的长,即可得到答案.
【详解】(1)证明:∵四边形是菱形
∴
∵
∴
∴四边形是平行四边形
又∵
∴
∴四边形是矩形
(2)解:∵四边形是矩形,
∴
∵四边形是菱形,
∴,
∴在中,根据勾股定理可得
∴
【点睛】本题考查了矩形的判定与性质、菱形的性质、平行四边形的判定及勾股定理,熟练掌握矩形的判定与性质是解题的关键.
14.(1)见解析
(2),
【分析】(1)根据题意证明出,即可得证;
(2)根据已知条件和矩形的性质证明,得到,设,则,在中,由勾股定理得:,
即,解出的值即可求出的长,设,则,在中,根据勾股定理得:,即,解出的值即可求出的长.
【详解】(1)证明:,,
,
,
,
四边形是矩形;
(2)解:四边形是矩形,
,
在和中,
,
,
,
设,则,
在中,由勾股定理得:,
,
解得:,
,
设,则,
在中,根据勾股定理得:,
即,
解得:,
.
【点睛】本题考查了外角的定义,矩形的判定与性质,直角三角形全等的判定,勾股定理,熟练掌握以上知识点是解答本题的关键.
15.(1)见解析;
(2)当为的中点时,四边形是矩形,理由见解析.
【分析】此题考查矩形的判定,全等三角形的判定与性质,等边三角形的性质和平行四边形的判定,解题关键在于根据已知条件两组对边相互平行证明平行四边形.
(1)证出,再加上条件,可得,可得到;
(2)首先证明四边形是平行四边形,再证明,即可以证出四边形是矩形.
【详解】(1)证明:如图,
∵是等边三角形,
∴,,
∵,
∴,
∴,
∵(即),,
∴四边形是平行四边形;
∴,
在和中,
,
∴,
∴;
(2)解:当为的中点时,四边形是矩形,
理由:∵为的中点,
∴,
又由()证得:,
∴,
∵,即,
∴四边形是平行四边形
又∵是等边三角形,为的中点,
∴(三线合一),
∴,
∴四边形是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
