19.1.2.2 函数的表示方法 课件(共26张PPT)
文档属性
| 名称 | 19.1.2.2 函数的表示方法 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.1 函数
19.1.2.2 函数的表示方法
第19章 一次函数
学习目标
1.通过实例,理解函数的三种表示方法及优点.
2.能根据实际情况选择合适的函数的表示方法,并能解决问题.
新课引入
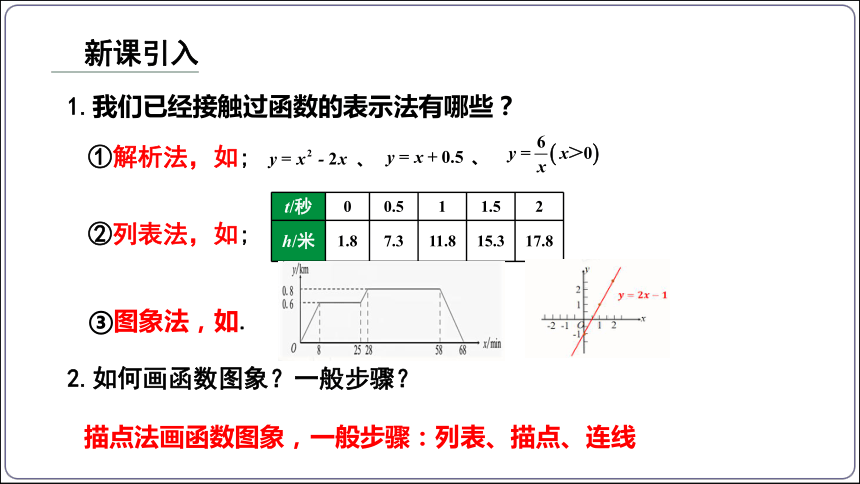
1.我们已经接触过函数的表示法有哪些?
①解析法,如;
②列表法,如;
③图象法,如.
t/秒 0 0.5 1 1.5 2
h/米 1.8 7.3 11.8 15.3 17.8
2.如何画函数图象?一般步骤?
描点法画函数图象,一般步骤:列表、描点、连线
思考:
1.如果想要知道函数之间的数量关系,选择哪种形式更方便呢?
3.如何选择合适的表示函数关系的表示方式呢?
2.如果能更直观地找到自变量对应的函数值,选择哪种更方便呢?
(1) 变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
解: y 是 x 的函数,自变量 x 的取值范围是 x > 0.
(2) 能求出 y 与 x 之间的函数解析式吗?
新知学习
探究
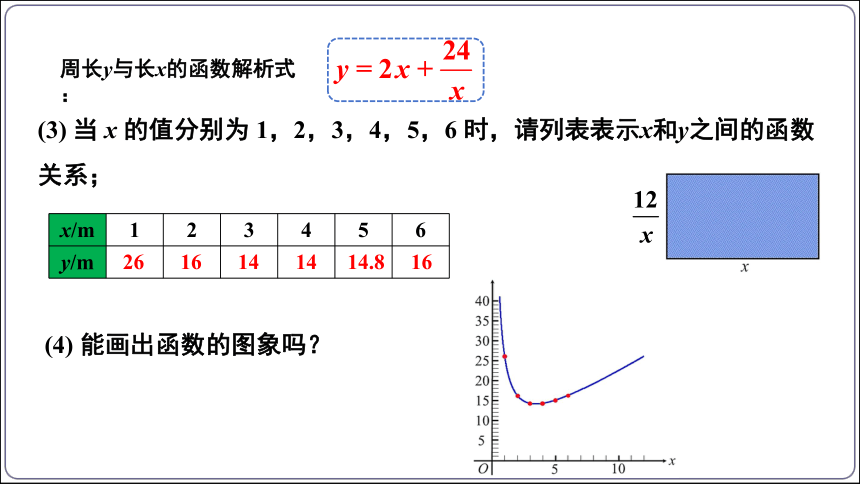
如图,要做一个面积为12m2 的花坛,该花坛的一边长为x m,周长为ym.
(3) 当 x 的值分别为 1,2,3,4,5,6 时,请列表表示x和y之间的函数关系;
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
(4) 能画出函数的图象吗?
周长y与长x的函数解析式:
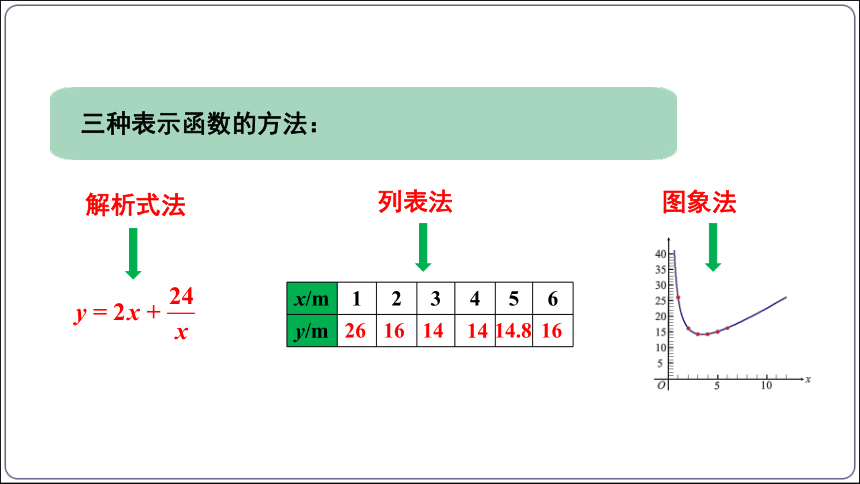
三种表示函数的方法:
解析式法
列表法
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
图象法
思考 (1) 对于每一个大于 0 的自变量的值,想准确求出自变量对应的函数值,选择哪种表示方?
解析式法
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
(2) 对于 x 的值分别为 1,2,3,4,5,6 时,能快速知道其对应的函数值,选择哪种表示方法?
列表法
图象法
(3) 想知道函数值 y 与自变量x之间的变化情况,选择哪种表示方法?
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
表示方法 定 义 优 点 缺 点
解析式法 用解析式来表示函数关系的方法 能准确地反映整个变化过程中自变量与函数的关系 不是所有函数都能用解析式法表示出来
列表法 用表格来表示函数关系的方法 由表中已有的自变量的每个值,可以直接得出相应的函数值 有局限性,自变量的值不能够一一列出,也不容易看出自变量与函数之间的对应关系
图象法 用图象来表示函数关系的方法 比较直观,可以反映出函数变化的趋势和某些性质 从图象中难以找到与自变量值对应的函数的准确值
函数的三种表示方法的特点:
例1 一个水库的水位在最近 5 h 内持续上涨,下表记录了这 5 h 内 6 个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
(1) 在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
解:(1) 如图,描出表中数据对应的点.可以看出,这 6 个点在一条直线上.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
再结合表中数据,可以发现每小时水位上升0.3m.
由此猜想,如果画出这5 h内其他时刻(如t=2.5 h等)及其水位高度所对应的点,它们可能也在这条直线上,
即在这个时间段中水位可能是始终以同一速度匀速上升的.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(2) 水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象. 这个函数能表示水位的变化规律吗?
解:由于水位在最近 5 h内持续上涨,对于时间 t 的每一个确定的值,水位高度 y 都有唯一的值与其对应,所以 y 是 t 的函数.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
开始时水位高度为3m,以后每小时水位升高0.3m.函数
y=0.3t+3(0≤t≤5 )
是符合表中数据的一个函数.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)列表;
(2)描点;
o
t/h
y /m
4.5
3
1 2 3 4 5
A
B
(3)连线 .
y = 0.3t+3
如果在这 5 h内,水位一直匀速上升,即升速为 0.3 m/h,那么函数y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.即使在这5h内,水位的升速有些变化,而由于每小时水位上升 0.3m 是确定的,因此这个函数也可以近似地表示水位的变化规律.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
o
t/h
y /m
4.5
3
5
A
B
y = 0.3t+3
由上面的例题可以看出,函数的不同表示法之间可以转化.
(3) 据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米.
法一:解析式求:
如果水位的变化规律不变,可利用函数预测,再过 2 h,即 t=5+2=7(h) 时,水位高度y=0.3×7+3=5.1(m).
(3) 据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米.
o
t/h
y /m
4.5
3
5
A
B
y = 0.3t+3
7
5.1
法二:图象法:
把图中的函数图象(线段AB)向右延伸到 t=7 所对应的位置,如图,从图象也能看出这时的水位高度约为 5.1 m.
(3) 据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米.
法三:表格法:
观察表格中数据的规律 ,可以发现每小时水位上升0.3m.由此猜想,如果再过2 h(t=7 h)水位高度约为 5.1 m.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
6
4.8
5.1
7
随堂练习
1.用列表法与解析式法表示n边形的内角和m(单位:度)关于边数n的函数.
解:列表如下:
边数 n 3 4 5 ……
内角和 m/度 …
180
360
540
解析式为m=180(n-2),n≥3,且n为整数.
2.一条小船沿直线向码头匀速前进. 在 0 min,2 min,4 min,6 min 时,测得小船与码头的距离分别为 200 m, 150 m,100 m,50 m. 小船与码头的距离 s 是时间 t 的函数吗?如果是,写出函数解析式,并画出函数图象. 如果船速不变,多长时间后小船到达码头?
解:小船与码头的距离 s 是时间 t 的函数.
由题意得,小船的速度为 50÷2=25(m/min),
则函数关系式为 s=200-25t (0≤t≤8) ,
函数图象如图所示:
x
y
O
1
2
3
5
4
6
7
50
100
150
200
8
y=200-25x(0≤x≤8)
由图象可知,若船速不变8 min后船到码头.
3.甲、乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设x s(0 ≤ x ≤ 100)后两车相距 y m.用解析式和图象表示y与x的对应关系.
解:甲、乙两车相距距离y与时间x之间的关系式为: y= 500-(25x-20x)=-5x+500
函数图象如图所示:
o
x(秒)
y (米)
500
400
300
200
100
10 20 30 40 50 60 70 80 90 100
y = -5x+500
课堂小结
函数的
表示方法
表示方法 定 义 优 点 缺 点
解析式法 用解析式来表示函数关系的方法 能准确地反映整个变化过程中自变量与函数的关系 不是所有函数都能用解析式法表示出来
列表法 用表格来表示函数关系的方法 由表中已有的自变量的每个值,可以直接得出相应的函数值 有局限性,自变量的值不能够一一列出,也不容易看出自变量与函数之间的对应关系
图象法 用图象来表示函数关系的方法 比较直观,可以反映出函数变化的趋势和某些性质 从图象中难以找到与自变量值对应的函数的准确值
函数的三种表示方法及特点:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.1 函数
19.1.2.2 函数的表示方法
第19章 一次函数
学习目标
1.通过实例,理解函数的三种表示方法及优点.
2.能根据实际情况选择合适的函数的表示方法,并能解决问题.
新课引入
1.我们已经接触过函数的表示法有哪些?
①解析法,如;
②列表法,如;
③图象法,如.
t/秒 0 0.5 1 1.5 2
h/米 1.8 7.3 11.8 15.3 17.8
2.如何画函数图象?一般步骤?
描点法画函数图象,一般步骤:列表、描点、连线
思考:
1.如果想要知道函数之间的数量关系,选择哪种形式更方便呢?
3.如何选择合适的表示函数关系的表示方式呢?
2.如果能更直观地找到自变量对应的函数值,选择哪种更方便呢?
(1) 变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
解: y 是 x 的函数,自变量 x 的取值范围是 x > 0.
(2) 能求出 y 与 x 之间的函数解析式吗?
新知学习
探究
如图,要做一个面积为12m2 的花坛,该花坛的一边长为x m,周长为ym.
(3) 当 x 的值分别为 1,2,3,4,5,6 时,请列表表示x和y之间的函数关系;
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
(4) 能画出函数的图象吗?
周长y与长x的函数解析式:
三种表示函数的方法:
解析式法
列表法
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
图象法
思考 (1) 对于每一个大于 0 的自变量的值,想准确求出自变量对应的函数值,选择哪种表示方?
解析式法
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
(2) 对于 x 的值分别为 1,2,3,4,5,6 时,能快速知道其对应的函数值,选择哪种表示方法?
列表法
图象法
(3) 想知道函数值 y 与自变量x之间的变化情况,选择哪种表示方法?
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
表示方法 定 义 优 点 缺 点
解析式法 用解析式来表示函数关系的方法 能准确地反映整个变化过程中自变量与函数的关系 不是所有函数都能用解析式法表示出来
列表法 用表格来表示函数关系的方法 由表中已有的自变量的每个值,可以直接得出相应的函数值 有局限性,自变量的值不能够一一列出,也不容易看出自变量与函数之间的对应关系
图象法 用图象来表示函数关系的方法 比较直观,可以反映出函数变化的趋势和某些性质 从图象中难以找到与自变量值对应的函数的准确值
函数的三种表示方法的特点:
例1 一个水库的水位在最近 5 h 内持续上涨,下表记录了这 5 h 内 6 个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
(1) 在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
解:(1) 如图,描出表中数据对应的点.可以看出,这 6 个点在一条直线上.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
再结合表中数据,可以发现每小时水位上升0.3m.
由此猜想,如果画出这5 h内其他时刻(如t=2.5 h等)及其水位高度所对应的点,它们可能也在这条直线上,
即在这个时间段中水位可能是始终以同一速度匀速上升的.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(2) 水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象. 这个函数能表示水位的变化规律吗?
解:由于水位在最近 5 h内持续上涨,对于时间 t 的每一个确定的值,水位高度 y 都有唯一的值与其对应,所以 y 是 t 的函数.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
开始时水位高度为3m,以后每小时水位升高0.3m.函数
y=0.3t+3(0≤t≤5 )
是符合表中数据的一个函数.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)列表;
(2)描点;
o
t/h
y /m
4.5
3
1 2 3 4 5
A
B
(3)连线 .
y = 0.3t+3
如果在这 5 h内,水位一直匀速上升,即升速为 0.3 m/h,那么函数y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.即使在这5h内,水位的升速有些变化,而由于每小时水位上升 0.3m 是确定的,因此这个函数也可以近似地表示水位的变化规律.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
o
t/h
y /m
4.5
3
5
A
B
y = 0.3t+3
由上面的例题可以看出,函数的不同表示法之间可以转化.
(3) 据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米.
法一:解析式求:
如果水位的变化规律不变,可利用函数预测,再过 2 h,即 t=5+2=7(h) 时,水位高度y=0.3×7+3=5.1(m).
(3) 据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米.
o
t/h
y /m
4.5
3
5
A
B
y = 0.3t+3
7
5.1
法二:图象法:
把图中的函数图象(线段AB)向右延伸到 t=7 所对应的位置,如图,从图象也能看出这时的水位高度约为 5.1 m.
(3) 据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米.
法三:表格法:
观察表格中数据的规律 ,可以发现每小时水位上升0.3m.由此猜想,如果再过2 h(t=7 h)水位高度约为 5.1 m.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
6
4.8
5.1
7
随堂练习
1.用列表法与解析式法表示n边形的内角和m(单位:度)关于边数n的函数.
解:列表如下:
边数 n 3 4 5 ……
内角和 m/度 …
180
360
540
解析式为m=180(n-2),n≥3,且n为整数.
2.一条小船沿直线向码头匀速前进. 在 0 min,2 min,4 min,6 min 时,测得小船与码头的距离分别为 200 m, 150 m,100 m,50 m. 小船与码头的距离 s 是时间 t 的函数吗?如果是,写出函数解析式,并画出函数图象. 如果船速不变,多长时间后小船到达码头?
解:小船与码头的距离 s 是时间 t 的函数.
由题意得,小船的速度为 50÷2=25(m/min),
则函数关系式为 s=200-25t (0≤t≤8) ,
函数图象如图所示:
x
y
O
1
2
3
5
4
6
7
50
100
150
200
8
y=200-25x(0≤x≤8)
由图象可知,若船速不变8 min后船到码头.
3.甲、乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设x s(0 ≤ x ≤ 100)后两车相距 y m.用解析式和图象表示y与x的对应关系.
解:甲、乙两车相距距离y与时间x之间的关系式为: y= 500-(25x-20x)=-5x+500
函数图象如图所示:
o
x(秒)
y (米)
500
400
300
200
100
10 20 30 40 50 60 70 80 90 100
y = -5x+500
课堂小结
函数的
表示方法
表示方法 定 义 优 点 缺 点
解析式法 用解析式来表示函数关系的方法 能准确地反映整个变化过程中自变量与函数的关系 不是所有函数都能用解析式法表示出来
列表法 用表格来表示函数关系的方法 由表中已有的自变量的每个值,可以直接得出相应的函数值 有局限性,自变量的值不能够一一列出,也不容易看出自变量与函数之间的对应关系
图象法 用图象来表示函数关系的方法 比较直观,可以反映出函数变化的趋势和某些性质 从图象中难以找到与自变量值对应的函数的准确值
函数的三种表示方法及特点:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
