19.1.1.2 函数 课件(共35张PPT)
文档属性
| 名称 | 19.1.1.2 函数 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.1 函数
19.1.1.2 函数
第19章 一次函数
1..通过实例,了解函数的三种表示方法和函数的概念.
3. 能求简单实际问题中函数的解析式、自变量的取值范围及函数值.
学习目标
生活中充满了许许多多变化的量,你了解这些变量之间的关系吗?
高铁行驶的路程与行驶时间、速度有关
新课引入
运动消耗的能量与运动时间、激烈程度有关
抛出的篮球,篮球的高度和运动时间、抛掷点的位置有关
我们生活在一个瞬息万变的世界里,在这个世界里,许多东西相互之间有一定联系. 今天,我们就用数学的视角来研究和学习这些“变”与“不变”,看看这些量之间有何关系……
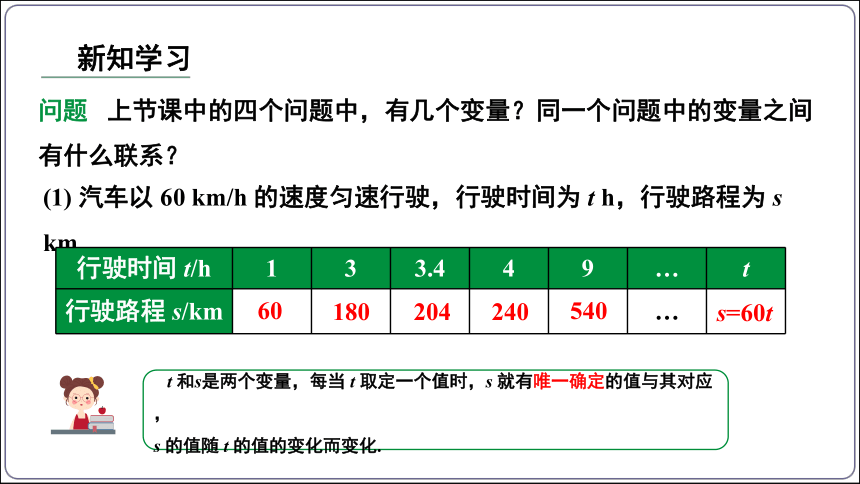
问题 上节课中的四个问题中,有几个变量?同一个问题中的变量之间有什么联系?
(1) 汽车以 60 km/h 的速度匀速行驶,行驶时间为 t h,行驶路程为 s km.
行驶时间 t/h 1 3 3.4 4 9 … t
行驶路程 s/km …
60
180
204
240
540
t 和s是两个变量,每当 t 取定一个值时,s 就有唯一确定的值与其对应,
s 的值随 t 的值的变化而变化.
新知学习
s=60t
(2) 每张电影票的售价为 10 元,第一场售出 150 张票,第二场售出 205张票,第三场售出 310 张票,三场电影的票房收入各多少元?设某场电影售出 x 张票,票房收入为 y 元.
当 x = 150 张时,y = 1500 元;
当 x = 205 张时,y = 2050 元;
当 x = 310 张时,y = 3100 元;
y = 10x.
x和y是两个变量,每当 x 取定一个值时,y 就有唯一确定的值与其对应,y 的值随 x 的值的变化而变化.
...
(3) 当圆的半径 r 为 10 cm,20 cm,30 cm 时,圆的面积 S 分别为多少?S 的值随 r 的值如何变化?
当 r = 10 cm 时,面积 S = 100π cm2;
当 r = 20 cm 时,面积 S = 400π cm2;
当 r = 30 cm 时,面积 S = 900π cm2;
S = πr2.
r和S是两个变量,每当 r 取定一个值时,S 就有唯一确定的值与其对应,S 的值随 r 的值的变化而变化.
...
当 x = 3 m 时,y = 2 m;
当 x = 3.5 m 时,y = 1.5 m;
当 x = 4 m 时,y = 1 m;
y = 5 - x.
(4) 用 10 m 长的绳子围一个矩形,当矩形的一边长 x 分别为 3 m,3. 5 m,4 m,4. 5 m 时,它的邻边长 y 分别为多少?y 的值随 x 的值如何变化?
x和y是两个变量,每当 x 取定一个值时,y 就有唯一确定的值与其对应,y 的值随 x 的值的变化而变化.
...
在上面的变化中,两个变量互相联系,当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
在生活中,经常还会用一些图或表格表达这种变化关系.一起来看看吧!
s=60t y = 10x S = πr2 y = 5 - x
1.下图是体检时的心电图,其中图上点的横坐标 x 表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量. 在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应吗?
对于 x 的每一个确定的值,y 都有唯一确定的值与其对应.
思考
2.下表是我国人口数统计表,年份与人口数可以分别记作两个变量 x 与 y,年份 x和人口数 y 是什么关系?
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
对于表中的每一个确定的年份 x,都对应着一个确定的人口数 y.
我们发现:在每一个变化过程中,都有两个变量 x 与 y ,并且对于x的每一个确定的值, y 都有唯一确定的值与其对应.
对于这样的关系我们该怎样定义呢?x 和 y 又代表什么含义呢?
如果当 x = a 时, y = b,那么 b 叫做当自变量的值为 a 时的函数值.
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
(1) 汽车以60km/h的速度匀速行驶,行驶路程为 s km,行驶时间为 t h.
3.你能指出下列问题中的自变量及函数吗?
(2) 体检时的心电图,横坐标时间x,纵坐标心脏部位的生物电流 y,它们是两个变量.
(3) 在我国人口数统计表,年份与人口数可以分别记作两个变量 x 和 y .
时间 t 是自变量
路程 s 是 t 的函数
时间 x是自变量
心脏部位的生物电流y是x的函数
年份x是自变量
人口数y是x的函数
s=60t
例1 汽车油箱中现有汽油 50L,如果不再加油,那么油箱中的油量 y (单位:L) 随行驶的路程 x (单位:km) 的增加而减少,耗油量 0.1 L/km.
(1) 写出表示 y 与 x 的函数关系的式子;
解:y 与 x 的函数关系式为:y = 50 - 0.1x.
像这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函数的解析式.
例1 汽车油箱中现有汽油 50L,如果不再加油,那么油箱中的油量
y (单位:L) 随行驶的路程 x (单位:km) 的增加而减少,耗油量
0.1 L/km.
(2) 指出自变量 x 的取值范围;
在实际问题中,函数的自变量取值范围往往是有限制的,要满足实际意义.我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
解: 从解析式y = 50 - 0.1x 看,x 可以取任意实数.
但 x 代表行驶路程,因此 x 不能取负数,
即 x ≥ 0.
又∵行驶中的耗油量为 0.1x,不能超过油箱中现有汽油量 50,
即 0.1x ≤ 50,
∴ x ≤ 500.
因此,自变量 x 的取值范围是:
0 ≤ x ≤ 500.
确定自变量的取值范围时,
不仅要考虑使函数关系式
有意义,而且还要注意问
题的实际意义.
例1 汽车油箱中现有汽油 50L,如果不再加油,那么油箱中的油量 y (单位:L) 随行驶的路程 x (单位:km) 的增加而减少,耗油量 0.1 L/km.
(3) 汽车行驶了 200km 时,油箱中还剩下多少汽油?
解:汽车行驶 200km 时,油箱中的汽油量是函数 y = 50 - 0.1x 在 x = 200 时的函数值.
将 x = 200 代入 y = 50 - 0.1x,得
y = 50 - 0.1×200 = 30.
汽车行驶了200km 时,油箱中还剩下汽油30L.
计算函数值时,自变量的取值要在其取值范围内.
例2 下列函数中自变量 x 的取值范围是什么?
.
0
.
-1
.
-2
x取全体实数
常见函数解析式中自变量的取值范围:
归纳总结
归纳总结
思考
4.函数的表示方法有哪些?
图象法
列表法
y = 50 - 0.1x
解析式法
随堂练习
1. 下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1) 改变正方形的边长 x,正方形的面积 S 随之变化.
自变量 x,S 是 x 的函数. S = x2 .
自变量 x,y 是 x 的函数. y = 0.1x .
(2) 每分钟向一水池注水 0.1 m3,注水量 y (单位: m3) 随注水时间 x (单位:min) 的变化而变化.
(3) 秀水村的耕地面积是 106 m2,这个村人均占有耕地面积 y (单位:m2) 随这个村人数 n 的变化而变化.
自变量 n,y 是 n 的函数. y = .
自变量 t ,V 是 t 的函数. V = 10 - 0.05t.
(4) 水池中有水 10 L,此后每小时漏水 0.05 L 水池中的水量 V (单位:L)随时间 t (单位:h) 的变化而变化.
(2)油箱中有油 30 kg,油从管道中匀速流出,1 h 流完,则油箱中剩余油量 Q (kg) 与流出时间 t (min) 之间的函数关系式是 ,自变量 t 的取值范围是 .
2. 填空
(1) 函数 中,自变量x的取值范围是 .
x ≥ 2
0 ≤ Q ≤ 30
3. 梯形的上底长 2 cm,高 3 cm,下底 x cm 大于上底长但不超过 5 cm.
写出梯形面积 S 关于 x 的函数解析式及自变量 x 的取值范围.
S = ,即 S = x + 3,
由题意可得x的取值范围是:2 < x ≤ 5.
解:
4.一次函数y 与 x 之间的函数关系式为:y = 15 - 0.5x,你可以在实际生活中找到它的应用场景吗?
解:(1)假设一个室内空间的初始温度为15℃,由于外部影响,温度每过一分钟下降0.5℃.这个降温过程可以用函数 y = 15 - 0.5x 来描述;
(2)价格和数量的关系:假设某种商品的单价是 15 元,每多买一件商品,价格就会减少 0.5 元.那么购买 n 件商品时的总价 y 与购买数量 x(件)之间的关系可以表示为 y = 15 - 0.5x.
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
课堂小结
概念
函数
函数解析式
函数值
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函数的解析式.
当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
自变量取值范围
函数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.1 函数
19.1.1.2 函数
第19章 一次函数
1..通过实例,了解函数的三种表示方法和函数的概念.
3. 能求简单实际问题中函数的解析式、自变量的取值范围及函数值.
学习目标
生活中充满了许许多多变化的量,你了解这些变量之间的关系吗?
高铁行驶的路程与行驶时间、速度有关
新课引入
运动消耗的能量与运动时间、激烈程度有关
抛出的篮球,篮球的高度和运动时间、抛掷点的位置有关
我们生活在一个瞬息万变的世界里,在这个世界里,许多东西相互之间有一定联系. 今天,我们就用数学的视角来研究和学习这些“变”与“不变”,看看这些量之间有何关系……
问题 上节课中的四个问题中,有几个变量?同一个问题中的变量之间有什么联系?
(1) 汽车以 60 km/h 的速度匀速行驶,行驶时间为 t h,行驶路程为 s km.
行驶时间 t/h 1 3 3.4 4 9 … t
行驶路程 s/km …
60
180
204
240
540
t 和s是两个变量,每当 t 取定一个值时,s 就有唯一确定的值与其对应,
s 的值随 t 的值的变化而变化.
新知学习
s=60t
(2) 每张电影票的售价为 10 元,第一场售出 150 张票,第二场售出 205张票,第三场售出 310 张票,三场电影的票房收入各多少元?设某场电影售出 x 张票,票房收入为 y 元.
当 x = 150 张时,y = 1500 元;
当 x = 205 张时,y = 2050 元;
当 x = 310 张时,y = 3100 元;
y = 10x.
x和y是两个变量,每当 x 取定一个值时,y 就有唯一确定的值与其对应,y 的值随 x 的值的变化而变化.
...
(3) 当圆的半径 r 为 10 cm,20 cm,30 cm 时,圆的面积 S 分别为多少?S 的值随 r 的值如何变化?
当 r = 10 cm 时,面积 S = 100π cm2;
当 r = 20 cm 时,面积 S = 400π cm2;
当 r = 30 cm 时,面积 S = 900π cm2;
S = πr2.
r和S是两个变量,每当 r 取定一个值时,S 就有唯一确定的值与其对应,S 的值随 r 的值的变化而变化.
...
当 x = 3 m 时,y = 2 m;
当 x = 3.5 m 时,y = 1.5 m;
当 x = 4 m 时,y = 1 m;
y = 5 - x.
(4) 用 10 m 长的绳子围一个矩形,当矩形的一边长 x 分别为 3 m,3. 5 m,4 m,4. 5 m 时,它的邻边长 y 分别为多少?y 的值随 x 的值如何变化?
x和y是两个变量,每当 x 取定一个值时,y 就有唯一确定的值与其对应,y 的值随 x 的值的变化而变化.
...
在上面的变化中,两个变量互相联系,当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
在生活中,经常还会用一些图或表格表达这种变化关系.一起来看看吧!
s=60t y = 10x S = πr2 y = 5 - x
1.下图是体检时的心电图,其中图上点的横坐标 x 表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量. 在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应吗?
对于 x 的每一个确定的值,y 都有唯一确定的值与其对应.
思考
2.下表是我国人口数统计表,年份与人口数可以分别记作两个变量 x 与 y,年份 x和人口数 y 是什么关系?
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
对于表中的每一个确定的年份 x,都对应着一个确定的人口数 y.
我们发现:在每一个变化过程中,都有两个变量 x 与 y ,并且对于x的每一个确定的值, y 都有唯一确定的值与其对应.
对于这样的关系我们该怎样定义呢?x 和 y 又代表什么含义呢?
如果当 x = a 时, y = b,那么 b 叫做当自变量的值为 a 时的函数值.
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
(1) 汽车以60km/h的速度匀速行驶,行驶路程为 s km,行驶时间为 t h.
3.你能指出下列问题中的自变量及函数吗?
(2) 体检时的心电图,横坐标时间x,纵坐标心脏部位的生物电流 y,它们是两个变量.
(3) 在我国人口数统计表,年份与人口数可以分别记作两个变量 x 和 y .
时间 t 是自变量
路程 s 是 t 的函数
时间 x是自变量
心脏部位的生物电流y是x的函数
年份x是自变量
人口数y是x的函数
s=60t
例1 汽车油箱中现有汽油 50L,如果不再加油,那么油箱中的油量 y (单位:L) 随行驶的路程 x (单位:km) 的增加而减少,耗油量 0.1 L/km.
(1) 写出表示 y 与 x 的函数关系的式子;
解:y 与 x 的函数关系式为:y = 50 - 0.1x.
像这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函数的解析式.
例1 汽车油箱中现有汽油 50L,如果不再加油,那么油箱中的油量
y (单位:L) 随行驶的路程 x (单位:km) 的增加而减少,耗油量
0.1 L/km.
(2) 指出自变量 x 的取值范围;
在实际问题中,函数的自变量取值范围往往是有限制的,要满足实际意义.我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
解: 从解析式y = 50 - 0.1x 看,x 可以取任意实数.
但 x 代表行驶路程,因此 x 不能取负数,
即 x ≥ 0.
又∵行驶中的耗油量为 0.1x,不能超过油箱中现有汽油量 50,
即 0.1x ≤ 50,
∴ x ≤ 500.
因此,自变量 x 的取值范围是:
0 ≤ x ≤ 500.
确定自变量的取值范围时,
不仅要考虑使函数关系式
有意义,而且还要注意问
题的实际意义.
例1 汽车油箱中现有汽油 50L,如果不再加油,那么油箱中的油量 y (单位:L) 随行驶的路程 x (单位:km) 的增加而减少,耗油量 0.1 L/km.
(3) 汽车行驶了 200km 时,油箱中还剩下多少汽油?
解:汽车行驶 200km 时,油箱中的汽油量是函数 y = 50 - 0.1x 在 x = 200 时的函数值.
将 x = 200 代入 y = 50 - 0.1x,得
y = 50 - 0.1×200 = 30.
汽车行驶了200km 时,油箱中还剩下汽油30L.
计算函数值时,自变量的取值要在其取值范围内.
例2 下列函数中自变量 x 的取值范围是什么?
.
0
.
-1
.
-2
x取全体实数
常见函数解析式中自变量的取值范围:
归纳总结
归纳总结
思考
4.函数的表示方法有哪些?
图象法
列表法
y = 50 - 0.1x
解析式法
随堂练习
1. 下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1) 改变正方形的边长 x,正方形的面积 S 随之变化.
自变量 x,S 是 x 的函数. S = x2 .
自变量 x,y 是 x 的函数. y = 0.1x .
(2) 每分钟向一水池注水 0.1 m3,注水量 y (单位: m3) 随注水时间 x (单位:min) 的变化而变化.
(3) 秀水村的耕地面积是 106 m2,这个村人均占有耕地面积 y (单位:m2) 随这个村人数 n 的变化而变化.
自变量 n,y 是 n 的函数. y = .
自变量 t ,V 是 t 的函数. V = 10 - 0.05t.
(4) 水池中有水 10 L,此后每小时漏水 0.05 L 水池中的水量 V (单位:L)随时间 t (单位:h) 的变化而变化.
(2)油箱中有油 30 kg,油从管道中匀速流出,1 h 流完,则油箱中剩余油量 Q (kg) 与流出时间 t (min) 之间的函数关系式是 ,自变量 t 的取值范围是 .
2. 填空
(1) 函数 中,自变量x的取值范围是 .
x ≥ 2
0 ≤ Q ≤ 30
3. 梯形的上底长 2 cm,高 3 cm,下底 x cm 大于上底长但不超过 5 cm.
写出梯形面积 S 关于 x 的函数解析式及自变量 x 的取值范围.
S = ,即 S = x + 3,
由题意可得x的取值范围是:2 < x ≤ 5.
解:
4.一次函数y 与 x 之间的函数关系式为:y = 15 - 0.5x,你可以在实际生活中找到它的应用场景吗?
解:(1)假设一个室内空间的初始温度为15℃,由于外部影响,温度每过一分钟下降0.5℃.这个降温过程可以用函数 y = 15 - 0.5x 来描述;
(2)价格和数量的关系:假设某种商品的单价是 15 元,每多买一件商品,价格就会减少 0.5 元.那么购买 n 件商品时的总价 y 与购买数量 x(件)之间的关系可以表示为 y = 15 - 0.5x.
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
课堂小结
概念
函数
函数解析式
函数值
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函数的解析式.
当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.
自变量取值范围
函数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
