19.2.2.4 一次函数的实际应用 课件(共34张PPT)
文档属性
| 名称 | 19.2.2.4 一次函数的实际应用 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 08:49:47 | ||
图片预览








文档简介
(共34张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.2 一次函数
19.2.2.4
一次函数的实际应用
第19章 一次函数
1. 能解决一次函数简单的实际问题.
2. 了解分段函数的表示及其图象的意义,并能决绝相关问题.
学习目标
新课引入
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
据说篮球巨人姚明的鞋子长31cm,那么你怎么判断他穿多大码的鞋子呢?
O
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
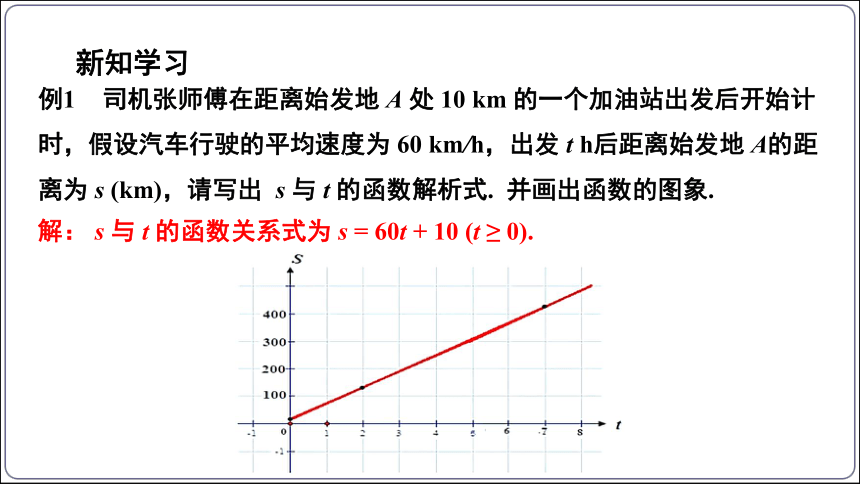
例1 司机张师傅在距离始发地 A 处 10 km 的一个加油站出发后开始计时,假设汽车行驶的平均速度为 60 km/h,出发 t h后距离始发地 A的距离为 s (km),请写出 s 与 t 的函数解析式. 并画出函数的图象.
解: s 与 t 的函数关系式为 s = 60t + 10 (t ≥ 0).
新知学习
例2 “黄金 1 号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
(1) 填写下表:
购买种子数量\kg 0.5 1 1.5 2 2.5 3 3.5 4 ...
付款金额\元 ...
2.5
5
7.5
10
12
14
16
18
解:设购买量为 x 千克,付款金额为 y 元.
当 x>2 时,y = 4(x - 2) + 10 = 4x + 2.
当 0≤x≤2 时,y = 5x;
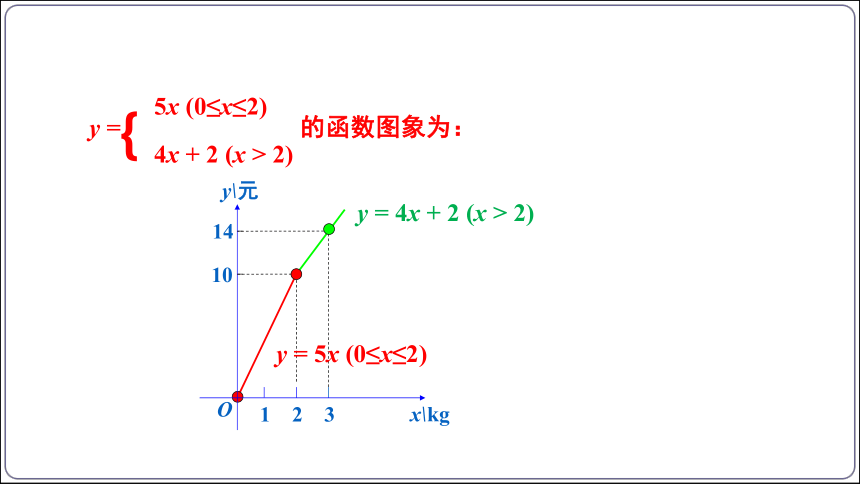
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
叫做分段函数.
注意:1.它是函数;
2.要写明每段自变量取值范围.
例2 “黄金 1 号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
的函数图象为:
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
思考
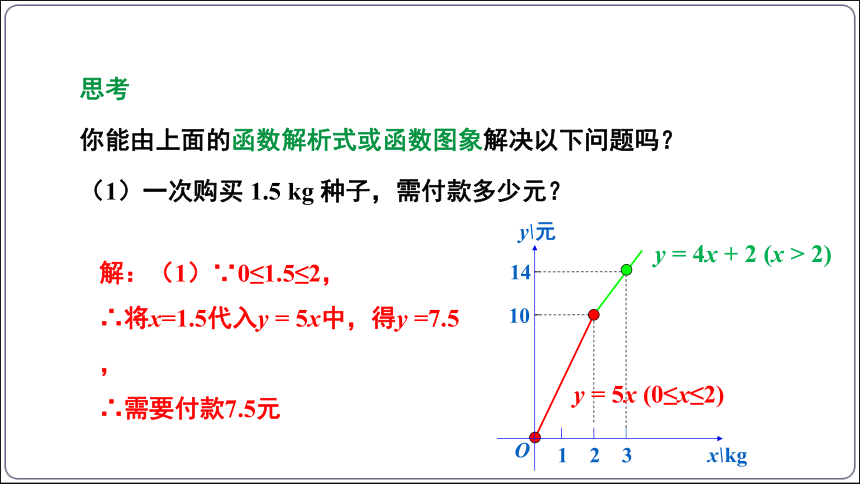
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买 1.5 kg 种子,需付款多少元?
解:(1)∵0≤1.5≤2,
∴将x=1.5代入y = 5x中,得y =7.5,
∴需要付款7.5元
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
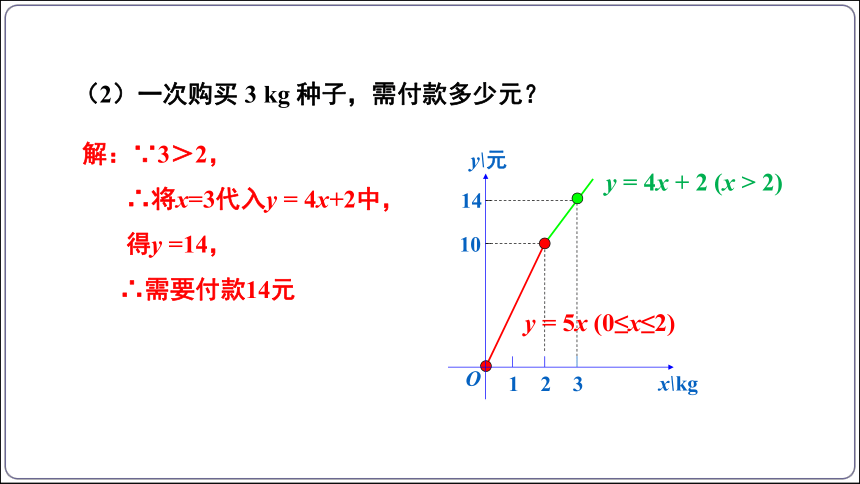
(2)一次购买 3 kg 种子,需付款多少元?
解:∵3>2,
∴将x=3代入y = 4x+2中,
得y =14,
∴需要付款14元
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
(3)32 元最多能购买多少种子?
解:当y =32>10,
∴满足函数 y = 4x + 2 (x > 2)
∴将y =32代入y =4x + 2中,得
4x + 2=32,
得x =7.5
∴32 元最多能购买7.5kg种子
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
变式1(2024 长春)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶 小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,
测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.
(1)a的值为______;
(2)当1≤x≤a时,求y与x之间的函数关系式;
解:由题可得1≤x≤ ,
∴设y=kx+b,将( ,17),( ,20)代入,
k+b=17
k+b=20 ,
得
解得:
k=90
b=2,
∴当1≤x≤ 时
y与x之间的函数关系式y=90x+2.
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米\时).
(3)将x= 代入y=90x+2,得y=
∴减速前行驶的路程为 千米,
∴减速前的速度为 ÷ =114千米\时,
∵114<120,
所以该辆汽车减速前没有超速.
变式2(2024 牡丹江)一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早 小时到达目的地.甲、乙两车之间的路程与两车行驶时间的函数关系如图所示,请结合图象信息,解答下列问题:
A
B
C
甲
乙
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
(1)甲车行驶的速度是_________;
分析:由图可知,甲车 小时行驶的路程为(200-180)km,
∴甲车行驶的速度是(200-180)÷ =70(km\h)
70km\h
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
解:由图可知,E( ,0),F(4,180)
设线段EF所在直线的解析式为y=kx+b,
则
解得
线段EF所在直线的函数解析式为y=120x-300.
(2)求图中线段EF所在直线的函数解析式(不要求写出自变量的取值范围);
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
A
B
C
甲
乙
300
解:由题意知,A、C两地的距离为:
(4+ )×70=300(km),
乙车行驶的速度为:300÷ -70=50 (km\h),
C、B两地的距离为:50×4=200(km),
A、B两地的距离为:300-200=100(km),
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况,当在甲乙相遇前时,
即在线段DE上:
200-50x=3(100-70x),
解得x= ;
当甲乙相遇后时:
200-50x=3(70x-100),
解得x= ;
综上可知,两车出发 h或 h时,
乙车距B地的路程是甲车距B地路程的3倍.
A
B
C
甲
乙
100
200
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
300
方法总结
读懂折线形图象的方法:
(1)弄清楚横轴与纵轴所表示的函数变量;
(2)找起点:结合题干中所给自变量及因变量的取值范围,在图象中找相对应的点,将坐标转化为实际意义;
(3)拐点:图象上的拐点既是前一段函数的终点,又是后一段函数的起点,反映函数图象在这一时刻开始发生变化,说明运动状态发生了变化;
(4)水平线:函数值随自变量的变化而保持不变;
(5)交点:表示两个函数的自变量与函数值分别对应相等,这个交点是函数值大小关系的“分界点”
2.一个试验室在0:00—2:00保持20 ℃的恒温,在2:00—4:00 匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
分析:试验室温度不是固定不变的,它与时间有关.
当 0≤t≤2 时,试验室温度T为20 ℃;
当2<t≤4 时,试验室温度T关于时间t的解析式为T=20+5(t-2).
因此,写函数解析式与画函数图象时,应对 0≤t≤2 和2<t≤4 分段讨论.
随堂练习
解:当0≤t≤2 时,T=20.
当 2<t≤4 时,T=20+5(t-2)=5t+10.
函数图象如图所示.
∴T 与 t 的函数解析式为
T=
y
x
O
30
20
2
4
20, 0≤t≤2,
5x+10, 21. 节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水 w(L) 与滴水时间 t(h) 的关系用可以显示水量的容器做如图 1 的试验,并根据试验数据绘制出如图 2 的函数图象,结合图象解答下列问题.
(1) 容器内原有水多少升.
解:(1) 根据图象可知,t = 0 时,w = 0.3,即容器内原有水 0.3 升;
(2) 求 w 与 t 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
解:(2) 设 w 与 t 之间的函数关系式为 w = kt + b,将 (0 , 0.3),(1.5 , 0.9) 代入,
得: ,解得: ,
故 w 与 t 之间的函数关系式为 w = 0.4t + 0.3;
由解析式可知,每小时滴水量为 0.4L,一天的滴水量为:0.4×24 = 9.6L,
即在这种滴水状态下一天的滴水量是 9.6 升.
3. 某公司开发出一款新包装的牛奶,牛奶的成本价为 6 元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月 (30 天) 的试营销,售价为 8 元/盒. 前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前 12 天日销售量 y (盒) 与销售时间 x (天) 之间的函数关系,于是从第 13 天起采用打折销售 (不低于成本价),时间每增加 1 天,日销售量就增加 10 盒.
(1) 打折销售后,第 17 天的日销售量为 ________ 盒;
分析:(1) 由图象可得第 12 天的日销售量为 190 盒,
因为从第 13 天起采用打折销售 (不低于成本价),时间每增加 1 天,日销售量就增加 10 盒,
故日销售量比第 12 天增加 50 盒,为 240 盒;
240
(2) 求 y 与 x 之间的函数关系式,并写出 x 的取值范围;
解:(2) 当 1 ≤ x ≤ 12 时,
令 y = kx + b.
由图知:当 x = 1 时,y = 300;x = 12,y = 190.
∴ ,∴ ,
∴y = -10x + 310 (1 ≤ x ≤ 12).
当 12 < x ≤ 30 时,y = 190 + 10(x - 12).
∴y = 10x + 70 (12 < x ≤ 30).
∴
课堂小结
读懂折线形图象的方法:
(1)弄清楚横轴与纵轴所表示的函数变量;
(2)找起点:结合题干中所给自变量及因变量的取值范围,在图象中找相对应的点,将坐标转化为实际意义;
(3)拐点:图象上的拐点既是前一段函数的终点,又是后一段函数的起点,反映函数图象在这一时刻开始发生变化,说明运动状态发生了变化;
(4)水平线:函数值随自变量的变化而保持不变;
(5)交点:表示两个函数的自变量与函数值分别对应相等,这个交点是函数值大小关系的“分界点”
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.2 一次函数
19.2.2.4
一次函数的实际应用
第19章 一次函数
1. 能解决一次函数简单的实际问题.
2. 了解分段函数的表示及其图象的意义,并能决绝相关问题.
学习目标
新课引入
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
据说篮球巨人姚明的鞋子长31cm,那么你怎么判断他穿多大码的鞋子呢?
O
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
例1 司机张师傅在距离始发地 A 处 10 km 的一个加油站出发后开始计时,假设汽车行驶的平均速度为 60 km/h,出发 t h后距离始发地 A的距离为 s (km),请写出 s 与 t 的函数解析式. 并画出函数的图象.
解: s 与 t 的函数关系式为 s = 60t + 10 (t ≥ 0).
新知学习
例2 “黄金 1 号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
(1) 填写下表:
购买种子数量\kg 0.5 1 1.5 2 2.5 3 3.5 4 ...
付款金额\元 ...
2.5
5
7.5
10
12
14
16
18
解:设购买量为 x 千克,付款金额为 y 元.
当 x>2 时,y = 4(x - 2) + 10 = 4x + 2.
当 0≤x≤2 时,y = 5x;
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
叫做分段函数.
注意:1.它是函数;
2.要写明每段自变量取值范围.
例2 “黄金 1 号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
的函数图象为:
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
思考
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买 1.5 kg 种子,需付款多少元?
解:(1)∵0≤1.5≤2,
∴将x=1.5代入y = 5x中,得y =7.5,
∴需要付款7.5元
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
(2)一次购买 3 kg 种子,需付款多少元?
解:∵3>2,
∴将x=3代入y = 4x+2中,
得y =14,
∴需要付款14元
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
(3)32 元最多能购买多少种子?
解:当y =32>10,
∴满足函数 y = 4x + 2 (x > 2)
∴将y =32代入y =4x + 2中,得
4x + 2=32,
得x =7.5
∴32 元最多能购买7.5kg种子
y = 5x (0≤x≤2)
y = 4x + 2 (x > 2)
y\元
x\kg
O
1
2
10
3
14
变式1(2024 长春)区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20千米的区间测速路段,从该路段起点开始,他先匀速行驶 小时,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,
测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的路程y(千米)与在此路段行驶的时间x(时)之间的函数图象如图所示.
(1)a的值为______;
(2)当1≤x≤a时,求y与x之间的函数关系式;
解:由题可得1≤x≤ ,
∴设y=kx+b,将( ,17),( ,20)代入,
k+b=17
k+b=20 ,
得
解得:
k=90
b=2,
∴当1≤x≤ 时
y与x之间的函数关系式y=90x+2.
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.(此路段要求小型汽车行驶速度不得超过120千米\时).
(3)将x= 代入y=90x+2,得y=
∴减速前行驶的路程为 千米,
∴减速前的速度为 ÷ =114千米\时,
∵114<120,
所以该辆汽车减速前没有超速.
变式2(2024 牡丹江)一条公路上依次有A、B、C三地,甲车从A地出发,沿公路经B地到C地,乙车从C地出发,沿公路驶向B地.甲、乙两车同时出发,匀速行驶,乙车比甲车早 小时到达目的地.甲、乙两车之间的路程与两车行驶时间的函数关系如图所示,请结合图象信息,解答下列问题:
A
B
C
甲
乙
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
(1)甲车行驶的速度是_________;
分析:由图可知,甲车 小时行驶的路程为(200-180)km,
∴甲车行驶的速度是(200-180)÷ =70(km\h)
70km\h
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
解:由图可知,E( ,0),F(4,180)
设线段EF所在直线的解析式为y=kx+b,
则
解得
线段EF所在直线的函数解析式为y=120x-300.
(2)求图中线段EF所在直线的函数解析式(不要求写出自变量的取值范围);
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
(3)请直接写出两车出发多少小时,乙车距B地的路程是甲车距B地路程的3倍.
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
A
B
C
甲
乙
300
解:由题意知,A、C两地的距离为:
(4+ )×70=300(km),
乙车行驶的速度为:300÷ -70=50 (km\h),
C、B两地的距离为:50×4=200(km),
A、B两地的距离为:300-200=100(km),
设两车出发x小时,乙车距B地的路程是甲车距B地路程的3倍,
分两种情况,当在甲乙相遇前时,
即在线段DE上:
200-50x=3(100-70x),
解得x= ;
当甲乙相遇后时:
200-50x=3(70x-100),
解得x= ;
综上可知,两车出发 h或 h时,
乙车距B地的路程是甲车距B地路程的3倍.
A
B
C
甲
乙
100
200
甲乙在此时相遇
这一段表示乙到达目的地,甲行驶的路程
此段代表甲乙相向行驶
此段代表甲乙背向而行
此点表示AC的距离
300
方法总结
读懂折线形图象的方法:
(1)弄清楚横轴与纵轴所表示的函数变量;
(2)找起点:结合题干中所给自变量及因变量的取值范围,在图象中找相对应的点,将坐标转化为实际意义;
(3)拐点:图象上的拐点既是前一段函数的终点,又是后一段函数的起点,反映函数图象在这一时刻开始发生变化,说明运动状态发生了变化;
(4)水平线:函数值随自变量的变化而保持不变;
(5)交点:表示两个函数的自变量与函数值分别对应相等,这个交点是函数值大小关系的“分界点”
2.一个试验室在0:00—2:00保持20 ℃的恒温,在2:00—4:00 匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
分析:试验室温度不是固定不变的,它与时间有关.
当 0≤t≤2 时,试验室温度T为20 ℃;
当2<t≤4 时,试验室温度T关于时间t的解析式为T=20+5(t-2).
因此,写函数解析式与画函数图象时,应对 0≤t≤2 和2<t≤4 分段讨论.
随堂练习
解:当0≤t≤2 时,T=20.
当 2<t≤4 时,T=20+5(t-2)=5t+10.
函数图象如图所示.
∴T 与 t 的函数解析式为
T=
y
x
O
30
20
2
4
20, 0≤t≤2,
5x+10, 2
(1) 容器内原有水多少升.
解:(1) 根据图象可知,t = 0 时,w = 0.3,即容器内原有水 0.3 升;
(2) 求 w 与 t 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
解:(2) 设 w 与 t 之间的函数关系式为 w = kt + b,将 (0 , 0.3),(1.5 , 0.9) 代入,
得: ,解得: ,
故 w 与 t 之间的函数关系式为 w = 0.4t + 0.3;
由解析式可知,每小时滴水量为 0.4L,一天的滴水量为:0.4×24 = 9.6L,
即在这种滴水状态下一天的滴水量是 9.6 升.
3. 某公司开发出一款新包装的牛奶,牛奶的成本价为 6 元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月 (30 天) 的试营销,售价为 8 元/盒. 前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前 12 天日销售量 y (盒) 与销售时间 x (天) 之间的函数关系,于是从第 13 天起采用打折销售 (不低于成本价),时间每增加 1 天,日销售量就增加 10 盒.
(1) 打折销售后,第 17 天的日销售量为 ________ 盒;
分析:(1) 由图象可得第 12 天的日销售量为 190 盒,
因为从第 13 天起采用打折销售 (不低于成本价),时间每增加 1 天,日销售量就增加 10 盒,
故日销售量比第 12 天增加 50 盒,为 240 盒;
240
(2) 求 y 与 x 之间的函数关系式,并写出 x 的取值范围;
解:(2) 当 1 ≤ x ≤ 12 时,
令 y = kx + b.
由图知:当 x = 1 时,y = 300;x = 12,y = 190.
∴ ,∴ ,
∴y = -10x + 310 (1 ≤ x ≤ 12).
当 12 < x ≤ 30 时,y = 190 + 10(x - 12).
∴y = 10x + 70 (12 < x ≤ 30).
∴
课堂小结
读懂折线形图象的方法:
(1)弄清楚横轴与纵轴所表示的函数变量;
(2)找起点:结合题干中所给自变量及因变量的取值范围,在图象中找相对应的点,将坐标转化为实际意义;
(3)拐点:图象上的拐点既是前一段函数的终点,又是后一段函数的起点,反映函数图象在这一时刻开始发生变化,说明运动状态发生了变化;
(4)水平线:函数值随自变量的变化而保持不变;
(5)交点:表示两个函数的自变量与函数值分别对应相等,这个交点是函数值大小关系的“分界点”
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
