19.2.3.2 一次函数与二元一次方程组 课件(共26张PPT)
文档属性
| 名称 | 19.2.3.2 一次函数与二元一次方程组 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 09:50:35 | ||
图片预览




文档简介
(共26张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.2 一次函数
19.2.3.2
一次函数与二元一次方程组
第19章 一次函数
1. 知道一次函数与二元一次方程组之间的关系.
2. 能根据一次函数图象求方程组的解、不等式的解集.
学习目标
新课引入
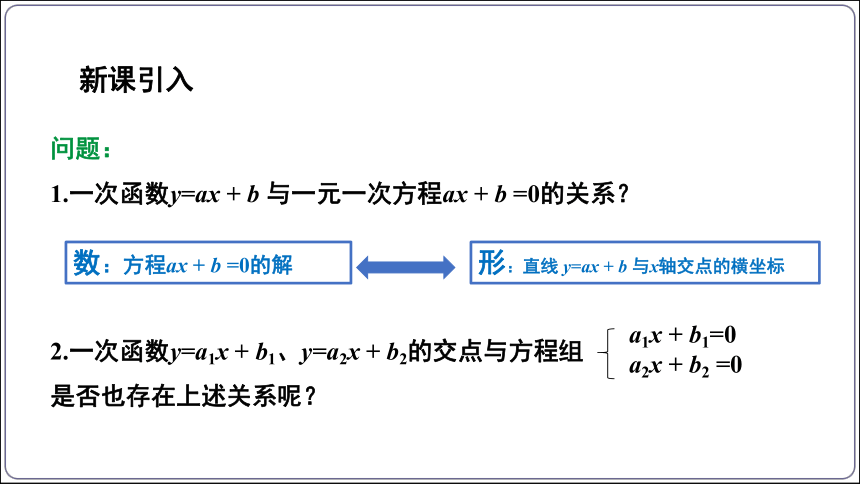
问题:
1.一次函数y=ax + b 与一元一次方程ax + b =0的关系?
数:方程ax + b =0的解
形:直线 y=ax + b 与x轴交点的横坐标
2.一次函数y=a1x + b1、y=a2x + b2的交点与方程组
是否也存在上述关系呢?
a1x + b1=0 a2x + b2 =0
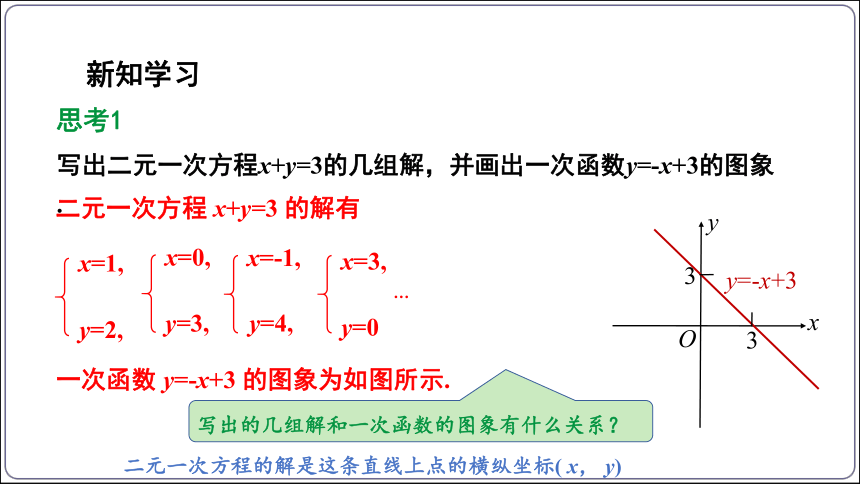
写出二元一次方程x+y=3的几组解,并画出一次函数y=-x+3的图象.
思考1
二元一次方程 x+y=3 的解有
x=1,
y=2,
x=-1,
y=4,
x=0,
y=3,
x=3,
y=0
一次函数 y=-x+3 的图象为如图所示.
y
x
O
3
3
y=-x+3
写出的几组解和一次函数的图象有什么关系?
…
新知学习
二元一次方程的解是这条直线上点的横纵坐标( x, y)
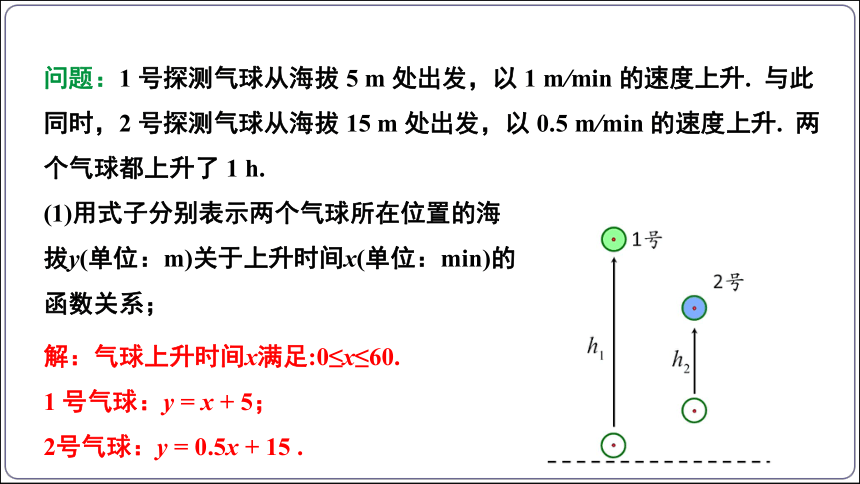
问题:1 号探测气球从海拔 5 m 处出发,以 1 m/min 的速度上升. 与此同时,2 号探测气球从海拔 15 m 处出发,以 0.5 m/min 的速度上升. 两个气球都上升了 1 h.
解:气球上升时间x满足:0≤x≤60.
1 号气球:y = x + 5;
2号气球:y = 0.5x + 15 .
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系;
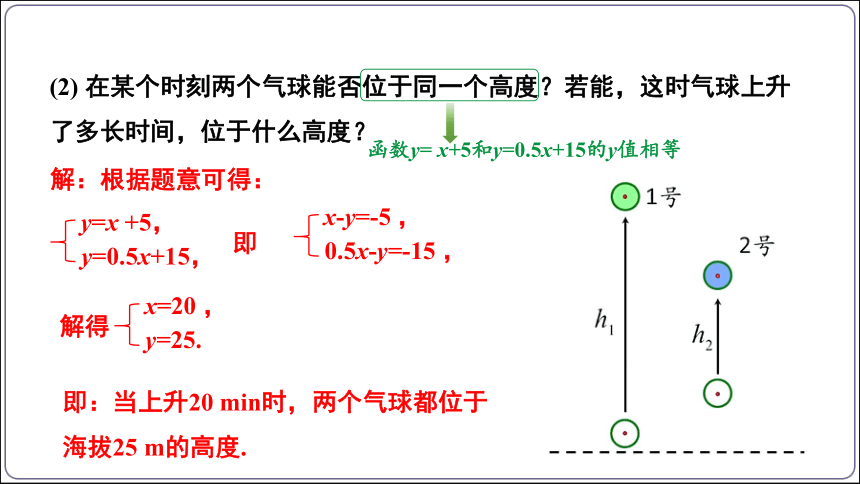
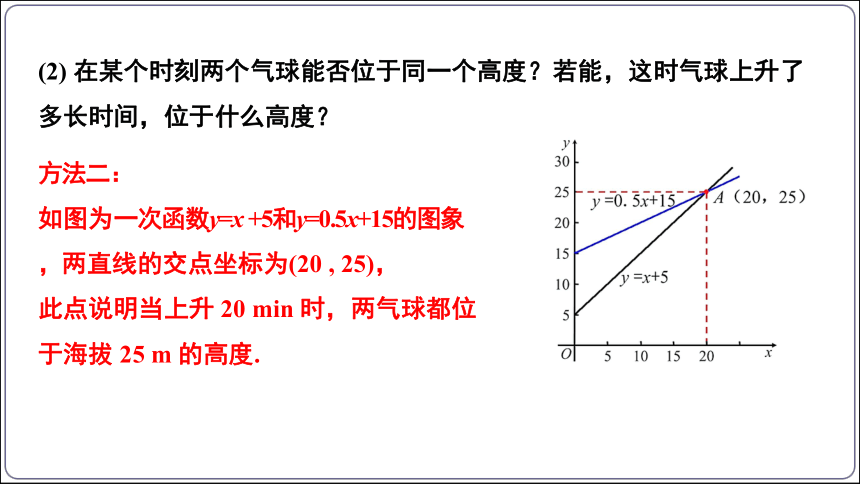
(2) 在某个时刻两个气球能否位于同一个高度?若能,这时气球上升了多长时间,位于什么高度?
函数y= x+5和y=0.5x+15的y值相等
y=x +5,
y=0.5x+15,
x-y=-5 ,
0.5x-y=-15 ,
解得
x=20 ,
y=25.
即:当上升20 min时,两个气球都位于海拔25 m的高度.
即
解:根据题意可得:
(2) 在某个时刻两个气球能否位于同一个高度?若能,这时气球上升了多长时间,位于什么高度?
方法二:
如图为一次函数y=x +5和y=0.5x+15的图象,两直线的交点坐标为(20 , 25),
此点说明当上升 20 min 时,两气球都位于海拔 25 m 的高度.
一般地,因为每个含有未知数 x和 y的二元一次方程,都可以改写为 y=kx+ b( k, b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标( x, y)都是这个二元一次方程的解.
一次函数与二元一次方程的关系:
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
y
x
O
P(x1, y1)
y=k1x +b1
y=k2x+b2
数:二元一次方程组 的解
形:直线y=k1x+b1 与直线y=k2x+b2 交点的横纵坐标
k1x +b1=0 (k1≠ 0) 解得: x=x1
k2x+b2=0 (k2≠ 0)
y=y1
一次函数与二元一次方程组的关系:
(x1,y1)是对应的二元一次方程组的解
所以交点坐标是(2,1).
x+y=3,
2x+y=5,
x=2,
y=1.
解:解法1:将直线 y=-x+3 和直线 y=-2x+5 转化为一个二元一次方程组,
即
例3 求直线 y=-x+3 和直线 y=-2x+5 的交点坐标.
解得
解法2:在同一平面直角坐标系中画出一次函数 y=-x+3和 y=-2x+5 的图象.
由图象可知交点坐标是(2,1).
y
x
O
y=-x+3
y=-2x+5
(2,1)
5
3
3
1
2
思考2
1.不等式3x + 2>x + 2的解集?
2.不等式3x + 2<x + 2的解集?
y=x + 2
x>0
x<0
3.求不等式组 的解集.
解:直线y=3x +2与x轴的交点坐标为( , 0),
y=x+2
∴不等式组的解集为:
-2 ≤ x ≤
归纳总结
P
y
x
O
y1=k1x+b1
y2=k2x+b2
直线 y1=k1x+b1 与直线y2=k2x+b2 的交点的横坐标即是方程 k1x+b1=k2x+b2的解;
直线 y1=k1x+b1 与直线y2=k2x+b2 的交点坐标即是二元一次方程组 的解;
不等式 y1>y2(或 y1k1x +b1=0 (k1≠ 0)
k2x+b2=0 (k2≠ 0)
例(2024 山西)如图,一次函数y=mx+n的图象与正比例函数
y=ax的图象交于点P(2,4).
(1)若直线y=mx+n与x轴交于点(-1,0),则关于x的方程mx+n=0的解为________;
(2)关于x,y的方程组 的解为________;
(3)不等式mx+n≤ax的解集为________.
x=-1
x≥2
1.如图所示,直线 l1 :y=x+6 与直线 l2 :y=-x-2 交于点 P(-2,3),不等式 x+6 > -x-2 的解集是( )
C. x<-2
A
D. x≤-2
A. x>-2
B. x≥-2
不等式 x+6 > -x-2的解集就是直线 l1 在直线 l2上方部分对应的 x 的取值范围.
随堂练习
x
y
3
-2
O
l
l
2.二元一次方程组 的解为_______.
分析:
方法一:两个式子矛盾,无解;
方法二:将方程组中的两个方程转化为两个一次函数,其自变量x的系数都为-1,且b不相等,说明两条直线平行,即图象无交点,所以二元一次方程组无解.
x+y=1,
x+y=3
y
x
O
y=1-x
y=-x+3
3
3
1
1
无解
3.考虑下面两种移动电话计费方式:
方式一 方式二
月租费/(元\月) 30 0
本地通话费/(元\min) 0.30 0.40
请用函数方法解答:何时两种计费方式费用相等.
解:由题意可得,
方式一:y=0.3x+30,
方式二:y=0.4x;
令0.3x+30=0.4x,
解得,x=300,即通话300分钟时两种计费方式费用相等.
4.求一次函数 l1: y=2x+2,l2 :y=-x+5 的图象与 x 轴围成的三角形的面积.
求三角形三个顶点的坐标
利用面积公式求三角形的面积
直线 l1 与 x 轴的交点坐标
直线 l2 与 x 轴的交点坐标
直线 l1 与 l2 的交点坐标
分析:
解:如图,画出函数图象,
设直线 l1,l2 交于点 A,两直线分别与 x 轴交于点 B,C.
令一次函数 y=2x+2=0,即 2x+2=0,
解得 x=-1,
∴ B (-1,0).
令一次函数 y=-x+5=0,即 -x+5=0,
解得 x=5,
∴C (5,0).
y=2x+2
y=-x+5
由 得
∴ A (1,4).
由图象易知 BC=6,
BC 边上的高,即为点 A 对应的纵坐标为 4,
故S△ABC= BC·yA= ×6×4=12.
一次函数
与二元一次方程组
课堂小结
一次函数与
二元一次方程(组)
一次函数与
二元一次不等式(组)
数:二元一次方程组 的解
形:直线y1=k1x+b1 与y2=k2x+b2 交点的横纵坐标
不等式 y1>y2(或 y1谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.2 一次函数
19.2.3.2
一次函数与二元一次方程组
第19章 一次函数
1. 知道一次函数与二元一次方程组之间的关系.
2. 能根据一次函数图象求方程组的解、不等式的解集.
学习目标
新课引入
问题:
1.一次函数y=ax + b 与一元一次方程ax + b =0的关系?
数:方程ax + b =0的解
形:直线 y=ax + b 与x轴交点的横坐标
2.一次函数y=a1x + b1、y=a2x + b2的交点与方程组
是否也存在上述关系呢?
a1x + b1=0 a2x + b2 =0
写出二元一次方程x+y=3的几组解,并画出一次函数y=-x+3的图象.
思考1
二元一次方程 x+y=3 的解有
x=1,
y=2,
x=-1,
y=4,
x=0,
y=3,
x=3,
y=0
一次函数 y=-x+3 的图象为如图所示.
y
x
O
3
3
y=-x+3
写出的几组解和一次函数的图象有什么关系?
…
新知学习
二元一次方程的解是这条直线上点的横纵坐标( x, y)
问题:1 号探测气球从海拔 5 m 处出发,以 1 m/min 的速度上升. 与此同时,2 号探测气球从海拔 15 m 处出发,以 0.5 m/min 的速度上升. 两个气球都上升了 1 h.
解:气球上升时间x满足:0≤x≤60.
1 号气球:y = x + 5;
2号气球:y = 0.5x + 15 .
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系;
(2) 在某个时刻两个气球能否位于同一个高度?若能,这时气球上升了多长时间,位于什么高度?
函数y= x+5和y=0.5x+15的y值相等
y=x +5,
y=0.5x+15,
x-y=-5 ,
0.5x-y=-15 ,
解得
x=20 ,
y=25.
即:当上升20 min时,两个气球都位于海拔25 m的高度.
即
解:根据题意可得:
(2) 在某个时刻两个气球能否位于同一个高度?若能,这时气球上升了多长时间,位于什么高度?
方法二:
如图为一次函数y=x +5和y=0.5x+15的图象,两直线的交点坐标为(20 , 25),
此点说明当上升 20 min 时,两气球都位于海拔 25 m 的高度.
一般地,因为每个含有未知数 x和 y的二元一次方程,都可以改写为 y=kx+ b( k, b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标( x, y)都是这个二元一次方程的解.
一次函数与二元一次方程的关系:
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
y
x
O
P(x1, y1)
y=k1x +b1
y=k2x+b2
数:二元一次方程组 的解
形:直线y=k1x+b1 与直线y=k2x+b2 交点的横纵坐标
k1x +b1=0 (k1≠ 0) 解得: x=x1
k2x+b2=0 (k2≠ 0)
y=y1
一次函数与二元一次方程组的关系:
(x1,y1)是对应的二元一次方程组的解
所以交点坐标是(2,1).
x+y=3,
2x+y=5,
x=2,
y=1.
解:解法1:将直线 y=-x+3 和直线 y=-2x+5 转化为一个二元一次方程组,
即
例3 求直线 y=-x+3 和直线 y=-2x+5 的交点坐标.
解得
解法2:在同一平面直角坐标系中画出一次函数 y=-x+3和 y=-2x+5 的图象.
由图象可知交点坐标是(2,1).
y
x
O
y=-x+3
y=-2x+5
(2,1)
5
3
3
1
2
思考2
1.不等式3x + 2>x + 2的解集?
2.不等式3x + 2<x + 2的解集?
y=x + 2
x>0
x<0
3.求不等式组 的解集.
解:直线y=3x +2与x轴的交点坐标为( , 0),
y=x+2
∴不等式组的解集为:
-2 ≤ x ≤
归纳总结
P
y
x
O
y1=k1x+b1
y2=k2x+b2
直线 y1=k1x+b1 与直线y2=k2x+b2 的交点的横坐标即是方程 k1x+b1=k2x+b2的解;
直线 y1=k1x+b1 与直线y2=k2x+b2 的交点坐标即是二元一次方程组 的解;
不等式 y1>y2(或 y1
k2x+b2=0 (k2≠ 0)
例(2024 山西)如图,一次函数y=mx+n的图象与正比例函数
y=ax的图象交于点P(2,4).
(1)若直线y=mx+n与x轴交于点(-1,0),则关于x的方程mx+n=0的解为________;
(2)关于x,y的方程组 的解为________;
(3)不等式mx+n≤ax的解集为________.
x=-1
x≥2
1.如图所示,直线 l1 :y=x+6 与直线 l2 :y=-x-2 交于点 P(-2,3),不等式 x+6 > -x-2 的解集是( )
C. x<-2
A
D. x≤-2
A. x>-2
B. x≥-2
不等式 x+6 > -x-2的解集就是直线 l1 在直线 l2上方部分对应的 x 的取值范围.
随堂练习
x
y
3
-2
O
l
l
2.二元一次方程组 的解为_______.
分析:
方法一:两个式子矛盾,无解;
方法二:将方程组中的两个方程转化为两个一次函数,其自变量x的系数都为-1,且b不相等,说明两条直线平行,即图象无交点,所以二元一次方程组无解.
x+y=1,
x+y=3
y
x
O
y=1-x
y=-x+3
3
3
1
1
无解
3.考虑下面两种移动电话计费方式:
方式一 方式二
月租费/(元\月) 30 0
本地通话费/(元\min) 0.30 0.40
请用函数方法解答:何时两种计费方式费用相等.
解:由题意可得,
方式一:y=0.3x+30,
方式二:y=0.4x;
令0.3x+30=0.4x,
解得,x=300,即通话300分钟时两种计费方式费用相等.
4.求一次函数 l1: y=2x+2,l2 :y=-x+5 的图象与 x 轴围成的三角形的面积.
求三角形三个顶点的坐标
利用面积公式求三角形的面积
直线 l1 与 x 轴的交点坐标
直线 l2 与 x 轴的交点坐标
直线 l1 与 l2 的交点坐标
分析:
解:如图,画出函数图象,
设直线 l1,l2 交于点 A,两直线分别与 x 轴交于点 B,C.
令一次函数 y=2x+2=0,即 2x+2=0,
解得 x=-1,
∴ B (-1,0).
令一次函数 y=-x+5=0,即 -x+5=0,
解得 x=5,
∴C (5,0).
y=2x+2
y=-x+5
由 得
∴ A (1,4).
由图象易知 BC=6,
BC 边上的高,即为点 A 对应的纵坐标为 4,
故S△ABC= BC·yA= ×6×4=12.
一次函数
与二元一次方程组
课堂小结
一次函数与
二元一次方程(组)
一次函数与
二元一次不等式(组)
数:二元一次方程组 的解
形:直线y1=k1x+b1 与y2=k2x+b2 交点的横纵坐标
不等式 y1>y2(或 y1
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
