19.3 课题学习 选择方案 课件(共32张PPT)
文档属性
| 名称 | 19.3 课题学习 选择方案 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 09:51:26 | ||
图片预览








文档简介
(共32张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.3 课题学习 选择方案
第19章 一次函数
1.会建立实际问题的数学模型,将实际问题转化为数学问题.
2.会用一次函数知识解决方案选择问题.
学习目标
新课引入
做一件事情,有时有不同的实施方案. 比较这些方案,从中选择最佳方案作为行动计划是非常必要的. 应用数学知识和方法对各种方案进行分析比较,可以帮助我们清楚地认识各种方案,做出理性的决策.
你怎样从多种方案中选择最佳方案呢?
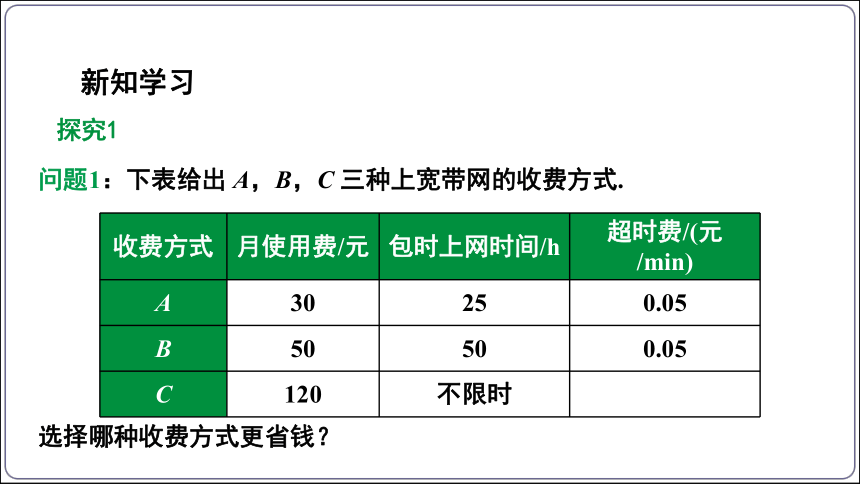
问题1:下表给出 A,B,C 三种上宽带网的收费方式.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选择哪种收费方式更省钱?
新知学习
探究1
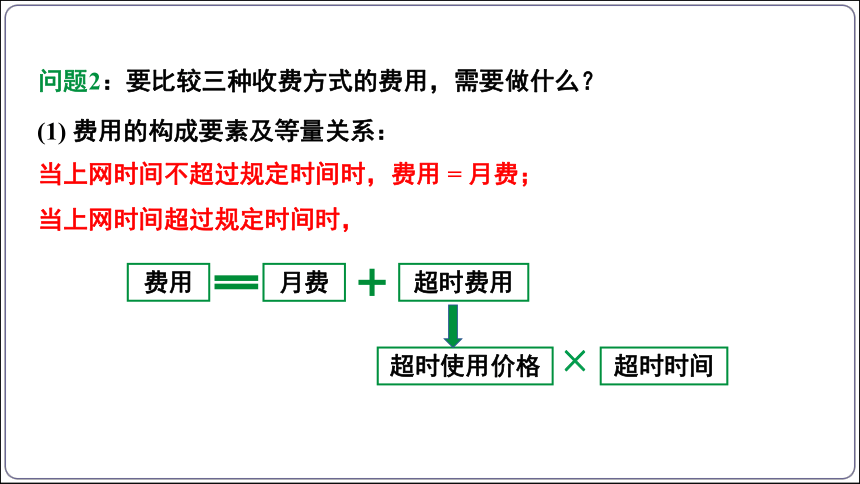
问题2:要比较三种收费方式的费用,需要做什么?
费用
月费
超时费用
超时使用价格
超时时间
(1) 费用的构成要素及等量关系:
当上网时间不超过规定时间时,费用 = 月费;
当上网时间超过规定时间时,
×
(2) 用适当方法表示出 A、B、C 两种方案的费用 (设上网时间为 t h).
①表示数量关系:
方式 A :
当上网时间不超过 25 h 时,费用 = 30 元;
当上网时间超过 25 h 时,费用 = 30+0.05×60(t - 25)元
y1=
方式 B :
当上网时间不超过 50 h 时,费用 = 50 元;
当上网时间超过 50 h 时,费用 = 50+0.05×60(t - 25)元.
尝试用表格形式表示数量关系
方式 C:120元.
y2=
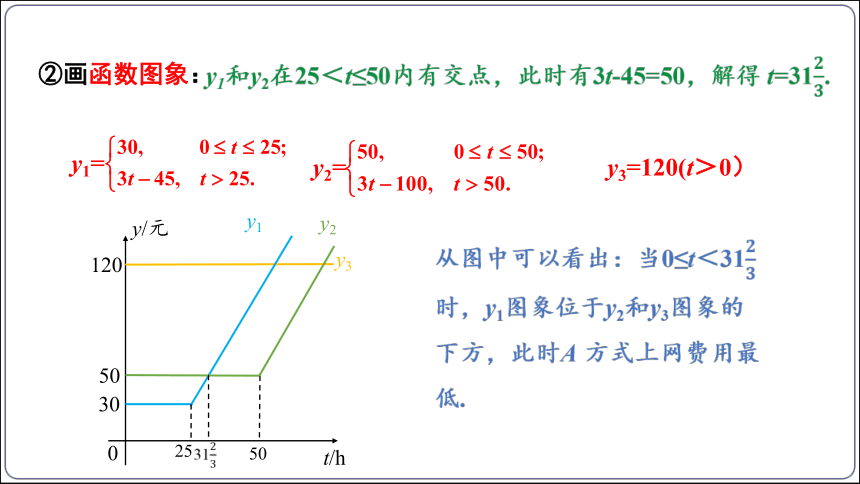
②画函数图象:
从图中可以看出:当0≤t<31时,y1图象位于y2和y3图象的下方,此时A 方式上网费用最低.
y1和y2在25<t≤50内有交点,此时有3t-45=50,解得 t=31.
0
30
50
25
50
120
y1
t/h
y/元
y3
y2
31
y1=
y2=
y3=120(t>0)
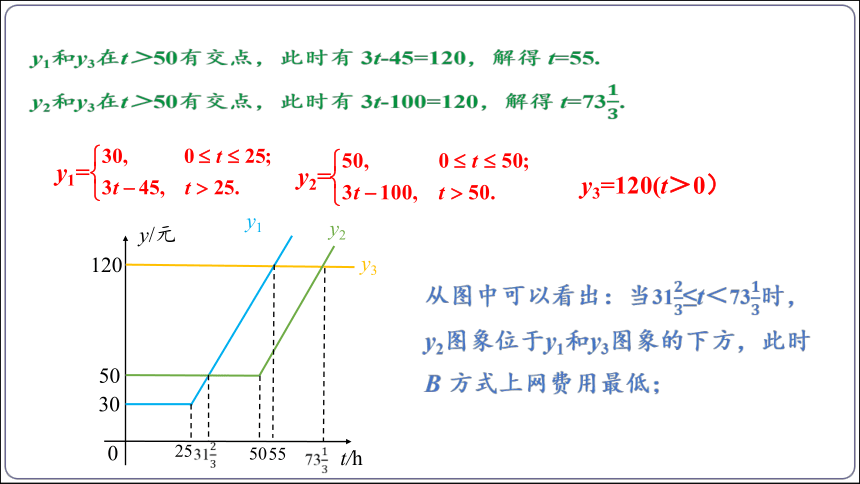
从图中可以看出:当31≤t<73时,y2图象位于y1和y3图象的下方,此时
B 方式上网费用最低;
y1和y3在t>50有交点,此时有 3t-45=120,解得 t=55.
y2和y3在t>50有交点,此时有 3t-100=120,解得 t=73.
0
30
50
25
50
120
y1
t/h
y/元
y3
y2
31
55
y1=
y2=
73
y3=120(t>0)
从图中可以看出:当t >73时,
y3图象位于y1和y2图象的下方,
C 方式上网费用最低.
0
30
50
25
50
120
y1
t/h
y/元
y3
y2
31
55
y1=
y2=
73
y3=120(t>0)
设上网时间为 t h,方案 A 的费用为 y1 元,方案 B 的费用为 y2 元,方案 C 的费用为 y3 元,则
y1 =
y2 =
y3 = 120, t ≥ 0.
③解答:
结合图象可知:
(1)当 y1 = y2,即 3t - 45 = 50,解方程得, t = ;
(2) 当y1 < y2,即 3t - 45 < 50,解不等式得, t < ;
(3) 当y1 > y2,即 3t - 45 > 50,解不等式得, t > ;
(4) 当y2 = y3,即 3t - 100 = 120得, t = ;
(5)当 y2 > y3,即 3t - 100 > 120得, t > .
0
30
50
25
50
120
y1
t
上网时间/h
y
上网
费用/元
y3
y2
31
55
73
y1=
y2=
y3=120(t>0)
即:
当上网时间为 ______________ 时,选择方案 A 最省钱;
当上网时间为 ______________ 时,选择方案 B 最省钱;
当上网时间为 ______________ 时,选择方案 C 最省钱.
t≤ h
h≤ t≤ h
t> h
0
30
50
25
50
120
y1
t
上网时间/h
y
上网
费用/元
y3
y2
31
55
73
某学校计划在总费用 2300 元的限额内,租用汽车送 234 名学生和 6 名教师集体外出活动,每辆汽车上至少有 1 名教师. 现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
(1) 共需租多少辆汽车?
(2) 给出最节省费用的租车方案.
探究2
(1) 需租多少辆汽车?
解:(1)∵(234+6)÷45=5(辆)……15(人),
∴保证240名师生都有车坐,每辆汽车上至少要有1名教师,
∴共需租6辆汽车.
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
总费用 2300 元
234 名学生和 6 名教师
(2) 给出最节省费用的租车方案.
解:设租乙种客车x辆,则甲种客车(6-x)辆,
由已知得:
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
总费用 2300 元
234 名学生和 6 名教师
解得:∵x为整数,
∴x=1或x=2.
设租车的总费用为y元,则y=280x+400×(6-x)=-120x+2400,
∵-120<0,
∴当x=2时,y取最小值,最小值为2160元.
故租甲种客车4辆、乙种客车2辆时,所需费用最低,最低费用为2160元.
学习了函数的图象及性质,我们可以利用函数图象的性质,直接求出最佳方案.
归纳总结
用一次函数选择最佳方案的一般步骤:
1.析:分析题意,弄清数量关系;
2.列:列出函数解析式;
3.求:根据函数图象求出不同取值时各函数的最小(最大)值;
4.选:结合实际需要选择最佳方案.
随堂练习
1.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6 000元,并且多买都有一定的优惠.各商场的优惠条件如下:
商场 优惠条件
甲商场 第一台按原报价收费,其余每台优惠25%
乙商场 每台优惠20%
(1)什么情况下到甲商场购买更优惠?
解:设学校购买x台电脑,选择甲商场时,所需费用为y1元,选择乙商场时,所需费用为y2元,
y1=6000+(1-25%)×6000(x-1)=4500x+1500;
y2=(1-20%)×6000x=4800x;
当 y1<y2时,有 4 500x+1 500<4 800x. 解得 x>5.
即当所购买电脑超过5台时,到甲商场购买更优惠.
商场 优惠条件
甲商场 第一台按原报价收费,其余每台优惠25%
乙商场 每台优惠20%
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
解:当y1>y2时,有4500x+1500>4 800x. 解得 x<5.
即当所购买电脑少于5台时,到乙商场买更优惠.
解:当 y1=y2 时,即4500x+1500=4800x. 解得x=5.
即当所购买电脑为5台时,两家商场的收费相同.
商场 优惠条件
甲商场 第一台按原报价收费,其余每台优惠25%
乙商场 每台优惠20%
2.云南的生活是美好中国带露珠的花朵,其中“云花”的年产量就高达180亿枝.已知某经销商购买甲种“云花”的费用y(元)与重量x(千克)之间的关系如图所示.购买乙种“云花”的价格为42元/千克.
(1)求y与x之间的函数解析式(解析式也称表达式);
解:(1)由题意得当0≤x≤70时,设y与x之间的函数解析式为y=kx,
将点(70,3 500)代入得3 500=70k,
解得k=50,∴y与x之间的函数解析式为y=50x;
当x>70时,设y与x之间的函数解析式为y=mx+n,
将点(70,3 500),(100,4 700)代入,得
∴y与x之间的函数解析式为y=40x+700.(x>70)
综上所述,y与x之间的函数解析式为y=
解得
(2)若甲种购买x千克,则乙种购买(100-x)千克,
①当60≤x≤70时,w=50x+42(100-x)=8x+4 200,
∵8>0,∴w随x的增大而增大,
∴当x=60时,w取最小值,此时w=8×60+4 200=4 680(元),
∴100-x=100-60=40(千克);
(2)该经销商计划一次性购进甲、乙两种“云花”共100千克,且要求甲种“云花”不少于60千克,但又不超过85千克.请你帮该经销商设计一种方案,应如何分配甲、乙两种“云花”的购买量,才能使经销商花费总金额w(元)最少?最少花费多少元?
②当70∵-2<0,∴w随x的增大而减小,
∴当x=85时,w取最小值,
此时w=-2×85+4 900=4 730(元),
∴100-x=100-85=15(千克),
∵4 680<4 730,
答:购进甲种“云花”60千克,乙种“云花”40千克时,经销商花费总金额w最少,最少花费4 680元.
课堂小结
用一次函数选择最佳方案的一般步骤
1.析:分析题意,弄清数量关系;
2.列:列出函数解析式、不等式或方程;
3.求:根据函数图象求出不同取值时各函数的值;
4.选:结合实际需要选择最佳方案.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.3 课题学习 选择方案
第19章 一次函数
1.会建立实际问题的数学模型,将实际问题转化为数学问题.
2.会用一次函数知识解决方案选择问题.
学习目标
新课引入
做一件事情,有时有不同的实施方案. 比较这些方案,从中选择最佳方案作为行动计划是非常必要的. 应用数学知识和方法对各种方案进行分析比较,可以帮助我们清楚地认识各种方案,做出理性的决策.
你怎样从多种方案中选择最佳方案呢?
问题1:下表给出 A,B,C 三种上宽带网的收费方式.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选择哪种收费方式更省钱?
新知学习
探究1
问题2:要比较三种收费方式的费用,需要做什么?
费用
月费
超时费用
超时使用价格
超时时间
(1) 费用的构成要素及等量关系:
当上网时间不超过规定时间时,费用 = 月费;
当上网时间超过规定时间时,
×
(2) 用适当方法表示出 A、B、C 两种方案的费用 (设上网时间为 t h).
①表示数量关系:
方式 A :
当上网时间不超过 25 h 时,费用 = 30 元;
当上网时间超过 25 h 时,费用 = 30+0.05×60(t - 25)元
y1=
方式 B :
当上网时间不超过 50 h 时,费用 = 50 元;
当上网时间超过 50 h 时,费用 = 50+0.05×60(t - 25)元.
尝试用表格形式表示数量关系
方式 C:120元.
y2=
②画函数图象:
从图中可以看出:当0≤t<31时,y1图象位于y2和y3图象的下方,此时A 方式上网费用最低.
y1和y2在25<t≤50内有交点,此时有3t-45=50,解得 t=31.
0
30
50
25
50
120
y1
t/h
y/元
y3
y2
31
y1=
y2=
y3=120(t>0)
从图中可以看出:当31≤t<73时,y2图象位于y1和y3图象的下方,此时
B 方式上网费用最低;
y1和y3在t>50有交点,此时有 3t-45=120,解得 t=55.
y2和y3在t>50有交点,此时有 3t-100=120,解得 t=73.
0
30
50
25
50
120
y1
t/h
y/元
y3
y2
31
55
y1=
y2=
73
y3=120(t>0)
从图中可以看出:当t >73时,
y3图象位于y1和y2图象的下方,
C 方式上网费用最低.
0
30
50
25
50
120
y1
t/h
y/元
y3
y2
31
55
y1=
y2=
73
y3=120(t>0)
设上网时间为 t h,方案 A 的费用为 y1 元,方案 B 的费用为 y2 元,方案 C 的费用为 y3 元,则
y1 =
y2 =
y3 = 120, t ≥ 0.
③解答:
结合图象可知:
(1)当 y1 = y2,即 3t - 45 = 50,解方程得, t = ;
(2) 当y1 < y2,即 3t - 45 < 50,解不等式得, t < ;
(3) 当y1 > y2,即 3t - 45 > 50,解不等式得, t > ;
(4) 当y2 = y3,即 3t - 100 = 120得, t = ;
(5)当 y2 > y3,即 3t - 100 > 120得, t > .
0
30
50
25
50
120
y1
t
上网时间/h
y
上网
费用/元
y3
y2
31
55
73
y1=
y2=
y3=120(t>0)
即:
当上网时间为 ______________ 时,选择方案 A 最省钱;
当上网时间为 ______________ 时,选择方案 B 最省钱;
当上网时间为 ______________ 时,选择方案 C 最省钱.
t≤ h
h≤ t≤ h
t> h
0
30
50
25
50
120
y1
t
上网时间/h
y
上网
费用/元
y3
y2
31
55
73
某学校计划在总费用 2300 元的限额内,租用汽车送 234 名学生和 6 名教师集体外出活动,每辆汽车上至少有 1 名教师. 现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
(1) 共需租多少辆汽车?
(2) 给出最节省费用的租车方案.
探究2
(1) 需租多少辆汽车?
解:(1)∵(234+6)÷45=5(辆)……15(人),
∴保证240名师生都有车坐,每辆汽车上至少要有1名教师,
∴共需租6辆汽车.
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
总费用 2300 元
234 名学生和 6 名教师
(2) 给出最节省费用的租车方案.
解:设租乙种客车x辆,则甲种客车(6-x)辆,
由已知得:
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
总费用 2300 元
234 名学生和 6 名教师
解得:
∴x=1或x=2.
设租车的总费用为y元,则y=280x+400×(6-x)=-120x+2400,
∵-120<0,
∴当x=2时,y取最小值,最小值为2160元.
故租甲种客车4辆、乙种客车2辆时,所需费用最低,最低费用为2160元.
学习了函数的图象及性质,我们可以利用函数图象的性质,直接求出最佳方案.
归纳总结
用一次函数选择最佳方案的一般步骤:
1.析:分析题意,弄清数量关系;
2.列:列出函数解析式;
3.求:根据函数图象求出不同取值时各函数的最小(最大)值;
4.选:结合实际需要选择最佳方案.
随堂练习
1.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6 000元,并且多买都有一定的优惠.各商场的优惠条件如下:
商场 优惠条件
甲商场 第一台按原报价收费,其余每台优惠25%
乙商场 每台优惠20%
(1)什么情况下到甲商场购买更优惠?
解:设学校购买x台电脑,选择甲商场时,所需费用为y1元,选择乙商场时,所需费用为y2元,
y1=6000+(1-25%)×6000(x-1)=4500x+1500;
y2=(1-20%)×6000x=4800x;
当 y1<y2时,有 4 500x+1 500<4 800x. 解得 x>5.
即当所购买电脑超过5台时,到甲商场购买更优惠.
商场 优惠条件
甲商场 第一台按原报价收费,其余每台优惠25%
乙商场 每台优惠20%
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
解:当y1>y2时,有4500x+1500>4 800x. 解得 x<5.
即当所购买电脑少于5台时,到乙商场买更优惠.
解:当 y1=y2 时,即4500x+1500=4800x. 解得x=5.
即当所购买电脑为5台时,两家商场的收费相同.
商场 优惠条件
甲商场 第一台按原报价收费,其余每台优惠25%
乙商场 每台优惠20%
2.云南的生活是美好中国带露珠的花朵,其中“云花”的年产量就高达180亿枝.已知某经销商购买甲种“云花”的费用y(元)与重量x(千克)之间的关系如图所示.购买乙种“云花”的价格为42元/千克.
(1)求y与x之间的函数解析式(解析式也称表达式);
解:(1)由题意得当0≤x≤70时,设y与x之间的函数解析式为y=kx,
将点(70,3 500)代入得3 500=70k,
解得k=50,∴y与x之间的函数解析式为y=50x;
当x>70时,设y与x之间的函数解析式为y=mx+n,
将点(70,3 500),(100,4 700)代入,得
∴y与x之间的函数解析式为y=40x+700.(x>70)
综上所述,y与x之间的函数解析式为y=
解得
(2)若甲种购买x千克,则乙种购买(100-x)千克,
①当60≤x≤70时,w=50x+42(100-x)=8x+4 200,
∵8>0,∴w随x的增大而增大,
∴当x=60时,w取最小值,此时w=8×60+4 200=4 680(元),
∴100-x=100-60=40(千克);
(2)该经销商计划一次性购进甲、乙两种“云花”共100千克,且要求甲种“云花”不少于60千克,但又不超过85千克.请你帮该经销商设计一种方案,应如何分配甲、乙两种“云花”的购买量,才能使经销商花费总金额w(元)最少?最少花费多少元?
②当70
∴当x=85时,w取最小值,
此时w=-2×85+4 900=4 730(元),
∴100-x=100-85=15(千克),
∵4 680<4 730,
答:购进甲种“云花”60千克,乙种“云花”40千克时,经销商花费总金额w最少,最少花费4 680元.
课堂小结
用一次函数选择最佳方案的一般步骤
1.析:分析题意,弄清数量关系;
2.列:列出函数解析式、不等式或方程;
3.求:根据函数图象求出不同取值时各函数的值;
4.选:结合实际需要选择最佳方案.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
