19.4 数学活动 课件(共25张PPT)
文档属性
| 名称 | 19.4 数学活动 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 09:52:26 | ||
图片预览







文档简介
(共25张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.4 数学活动
第19章 一次函数
1.能根据两个变量的部分对应值建立一次函数模型.
2.会用一次函数模型描述和研究时间问题的运动规律,对未来的情况作出估计.
3.经历根据两个变量的部分对应数据建立函数模型的过程,体会建立函数模型过程中的归纳思想,数形结合思想.
学习目标
新知学习
活动1 世界人口与年份的变化情况
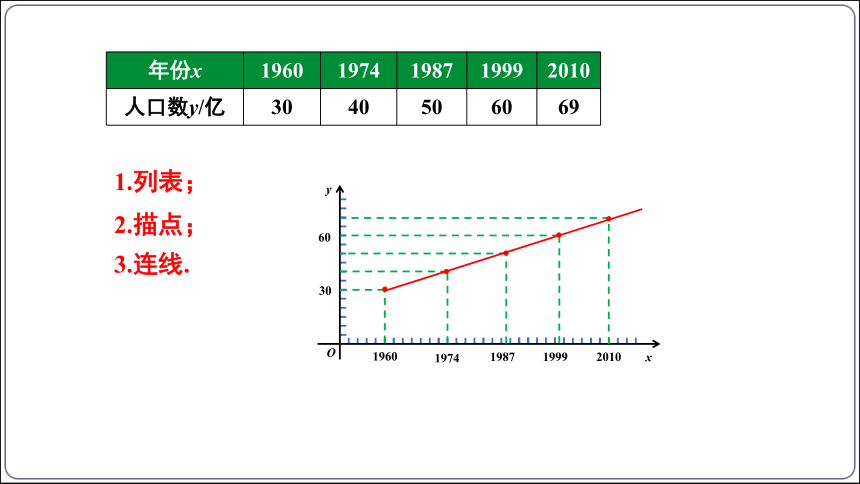
(1)根据下表的数据,在直角坐标系中画出世界人口增长的曲线图.
年份x 1960 1974 1987 1999 2010
人口数y/亿 30 40 50 60 69
你还记得画函数图象的方法吗?
列表--描点--连线
年份x 1960 1974 1987 1999 2010
人口数y/亿 30 40 50 60 69
1.列表;
2.描点;
3.连线.
O
y
x
30
60
1960
1974
1987
1999
2010
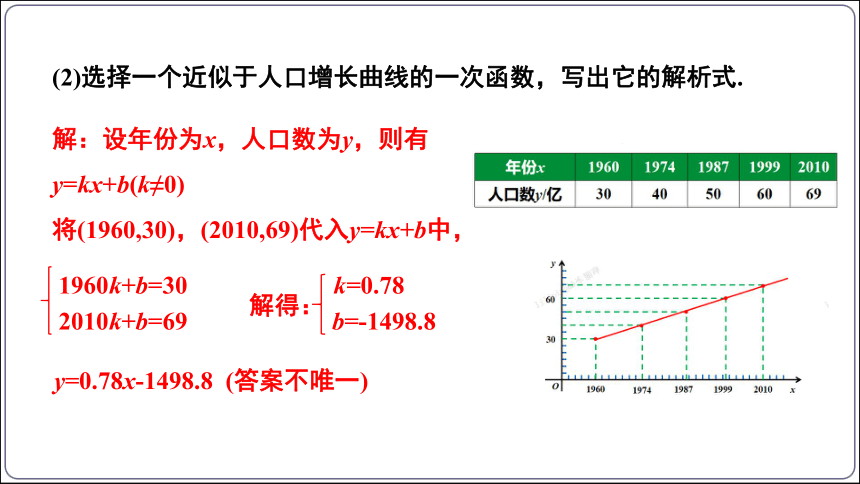
(2)选择一个近似于人口增长曲线的一次函数,写出它的解析式.
解:设年份为x,人口数为y,则有
y=kx+b(k≠0)
将(1960,30),(2010,69)代入y=kx+b中,
1960k+b=30
2010k+b=69
k=0.78
b=-1498.8
解得:
y=0.78x-1498.8 (答案不唯一)
(3)你能根据求出来的解析式估计2020年的世界人口数吗?
解:将x=2020代入到解析式y=0.78x-1498.8中,得
y=0.78×2020-1498.8=76.8(亿)
答:估计2020年的世界人口数将达到76.8亿.
活动2 水龙头漏水量与漏水时间的关系
水龙头关闭不严会造成滴水,为了调查漏水量和漏水时间的关系,可进行以下的试验和研究:
(1)在滴水的水龙头下放置一个能显示水量的容器,每5min记录一次容器中的水量,记录数据如下表:
时间t/min 0 5 10 15 20 25 30
水量w/mL 0 50 90 130 170 210 250
(2)建立直角坐标系,以横轴表示时间t,纵轴表示水量w,描出以上述试验所得数据为坐标的各点,并观察他们的分布规律.
时间t/min 0 5 10 15 20 25 30
水量w/mL 0 50 90 130 170 210 250
解:描点如图:
300
250
200
150
100
50
5 10 15 20 25 30
O
w/mL
t/min
由图可知,w随着t的增大而增大.
(3)试写出w关于t的函数解析式,并由它估算这种漏水状态下一天的漏水量.
将t=5,w=50和t=10,w=90代入,
解:这些点在同一条直线上.
设这条直线所对应的函数解析式为:w=kt+b(k≠0),
5k+b=50
10k+b=90 ,
得
解得:
k=8
b=10,
∴函数解析式为w=8t+10,
这种漏水状态下一天的漏水量为w=8×1440+10=11530mL.
1.(2024 广州)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一个函数关系,部分数据如下表:
脚长x(cm) ... 23 24 25 26 27 28 ...
身高y(cm) ... 156 163 170 177 184 191 ...
随堂练习
解图
脚长x(cm) ... 23 24 25 26 27 28 ...
身高y(cm) ... 156 163 170 177 184 191 ...
解:描点如图:
(1)在图①中描出表中数据对应的点(x,y);
(2)根据表中数据,从y=ax+b(a≠0)和y= (k≠0)中选择一个函数模型,使它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出x的取值范围);
∴函数y=ax+b(a≠0)能近似地反映身高和脚长的函数关系,
将点(23,156),(24,163)代入,
156= 23a+b
163=24a+b,
得
解: 由解图可知,y随着x的增大而增大,
解得:
a=7b=-5
a=7b=-5,
∴y=7x-5;
(3)如图②,某场所发现了一个人的脚印,脚长约为25.8cm,请根据(2)中求出的函数解析式 ,估计这个人的身高.
解:将 x=25.8代入 y=7x-5中,
得y=7×25.8-5=175.6,
∴估计这个人的身高为175.6cm.
2.(2024 四川甘孜州)端午节是我国的传统节日,有吃粽子的习俗.节日前夕,某商场购进A,B两种粽子共200盒进行销售.经了解,进价与标价如下表所示(单位:元/盒):
种类 进价 标价
A 90 120
B 50 60
(1)设该商场购进A种粽子x盒,销售两种粽子所得的总利润为y元,求y关于x的函数解析式(不必写出自变量x的取值范围);
解:(1)根据题意,y=(120-90)x+(60-50)(200-x)
=20x+2000,
∴ y关于x的函数解析式为y=20x+2000;
种类 进价 标价
A 90 120
B 50 60
(2)若购进的200盒粽子销售完毕,总利润不低于3 000元,请问至少需要购进A种粽子多少盒?
解:20x+2000≥3000,
解得:x≥50,
∴若购进的200盒粽子销售完毕,总利润不低于3000元,至少需要购进A种粽子50盒.
3.(2024 陕西)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从A市前往B市.他驾车从A市一高速公路入口驶入时,该车的剩余电量是80kW·h,行驶了240km后,从B市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示.
(1)求y与x之间的关系式;
将点(0,80),(150,50)代入y=kx+b中,
解:(1)设y与x之间的关系式为y=kx+b(k≠0),
80= b
50=150k+b,
得
解得:
k=
b=80,
(2)已知这辆车的“满电量”为100kW·h,求王师傅驾车从B市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.
∴y与x之间的关系式为y= x+80;
解:当x=240时,y= ×240+80=32,
∴该车的剩余电量占“满电量”的 ;
4.(2024 吉林)综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为xmm,凳面的宽度为ymm,记录如下:
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【分析数据】
如图③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.
将x=16.5,y=115.5和x=23.1,y=148.5代入,
解:(1)这些点在同一条直线上.
设这条直线所对应的函数解析式为:y=kx+b(k≠0),
16.5k+b=115.5
23.1k+b=148.5 ,
得
解得:
k=5
b=33,
∴函数解析式为y=5x+33,
经检验,其余点均在直线y=5x+33上,
∴这些点在同一条直线上,这条直线所对应的函数解析式为y=5x+33;
(2)当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?
解:把y=213代入y=5x+33得:
5x+33=213,
解得x=36,
∴当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度为36 mm.
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
19.4 数学活动
第19章 一次函数
1.能根据两个变量的部分对应值建立一次函数模型.
2.会用一次函数模型描述和研究时间问题的运动规律,对未来的情况作出估计.
3.经历根据两个变量的部分对应数据建立函数模型的过程,体会建立函数模型过程中的归纳思想,数形结合思想.
学习目标
新知学习
活动1 世界人口与年份的变化情况
(1)根据下表的数据,在直角坐标系中画出世界人口增长的曲线图.
年份x 1960 1974 1987 1999 2010
人口数y/亿 30 40 50 60 69
你还记得画函数图象的方法吗?
列表--描点--连线
年份x 1960 1974 1987 1999 2010
人口数y/亿 30 40 50 60 69
1.列表;
2.描点;
3.连线.
O
y
x
30
60
1960
1974
1987
1999
2010
(2)选择一个近似于人口增长曲线的一次函数,写出它的解析式.
解:设年份为x,人口数为y,则有
y=kx+b(k≠0)
将(1960,30),(2010,69)代入y=kx+b中,
1960k+b=30
2010k+b=69
k=0.78
b=-1498.8
解得:
y=0.78x-1498.8 (答案不唯一)
(3)你能根据求出来的解析式估计2020年的世界人口数吗?
解:将x=2020代入到解析式y=0.78x-1498.8中,得
y=0.78×2020-1498.8=76.8(亿)
答:估计2020年的世界人口数将达到76.8亿.
活动2 水龙头漏水量与漏水时间的关系
水龙头关闭不严会造成滴水,为了调查漏水量和漏水时间的关系,可进行以下的试验和研究:
(1)在滴水的水龙头下放置一个能显示水量的容器,每5min记录一次容器中的水量,记录数据如下表:
时间t/min 0 5 10 15 20 25 30
水量w/mL 0 50 90 130 170 210 250
(2)建立直角坐标系,以横轴表示时间t,纵轴表示水量w,描出以上述试验所得数据为坐标的各点,并观察他们的分布规律.
时间t/min 0 5 10 15 20 25 30
水量w/mL 0 50 90 130 170 210 250
解:描点如图:
300
250
200
150
100
50
5 10 15 20 25 30
O
w/mL
t/min
由图可知,w随着t的增大而增大.
(3)试写出w关于t的函数解析式,并由它估算这种漏水状态下一天的漏水量.
将t=5,w=50和t=10,w=90代入,
解:这些点在同一条直线上.
设这条直线所对应的函数解析式为:w=kt+b(k≠0),
5k+b=50
10k+b=90 ,
得
解得:
k=8
b=10,
∴函数解析式为w=8t+10,
这种漏水状态下一天的漏水量为w=8×1440+10=11530mL.
1.(2024 广州)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一个函数关系,部分数据如下表:
脚长x(cm) ... 23 24 25 26 27 28 ...
身高y(cm) ... 156 163 170 177 184 191 ...
随堂练习
解图
脚长x(cm) ... 23 24 25 26 27 28 ...
身高y(cm) ... 156 163 170 177 184 191 ...
解:描点如图:
(1)在图①中描出表中数据对应的点(x,y);
(2)根据表中数据,从y=ax+b(a≠0)和y= (k≠0)中选择一个函数模型,使它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出x的取值范围);
∴函数y=ax+b(a≠0)能近似地反映身高和脚长的函数关系,
将点(23,156),(24,163)代入,
156= 23a+b
163=24a+b,
得
解: 由解图可知,y随着x的增大而增大,
解得:
a=7b=-5
a=7b=-5,
∴y=7x-5;
(3)如图②,某场所发现了一个人的脚印,脚长约为25.8cm,请根据(2)中求出的函数解析式 ,估计这个人的身高.
解:将 x=25.8代入 y=7x-5中,
得y=7×25.8-5=175.6,
∴估计这个人的身高为175.6cm.
2.(2024 四川甘孜州)端午节是我国的传统节日,有吃粽子的习俗.节日前夕,某商场购进A,B两种粽子共200盒进行销售.经了解,进价与标价如下表所示(单位:元/盒):
种类 进价 标价
A 90 120
B 50 60
(1)设该商场购进A种粽子x盒,销售两种粽子所得的总利润为y元,求y关于x的函数解析式(不必写出自变量x的取值范围);
解:(1)根据题意,y=(120-90)x+(60-50)(200-x)
=20x+2000,
∴ y关于x的函数解析式为y=20x+2000;
种类 进价 标价
A 90 120
B 50 60
(2)若购进的200盒粽子销售完毕,总利润不低于3 000元,请问至少需要购进A种粽子多少盒?
解:20x+2000≥3000,
解得:x≥50,
∴若购进的200盒粽子销售完毕,总利润不低于3000元,至少需要购进A种粽子50盒.
3.(2024 陕西)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从A市前往B市.他驾车从A市一高速公路入口驶入时,该车的剩余电量是80kW·h,行驶了240km后,从B市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示.
(1)求y与x之间的关系式;
将点(0,80),(150,50)代入y=kx+b中,
解:(1)设y与x之间的关系式为y=kx+b(k≠0),
80= b
50=150k+b,
得
解得:
k=
b=80,
(2)已知这辆车的“满电量”为100kW·h,求王师傅驾车从B市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.
∴y与x之间的关系式为y= x+80;
解:当x=240时,y= ×240+80=32,
∴该车的剩余电量占“满电量”的 ;
4.(2024 吉林)综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为xmm,凳面的宽度为ymm,记录如下:
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【分析数据】
如图③,小组根据表中x,y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.
将x=16.5,y=115.5和x=23.1,y=148.5代入,
解:(1)这些点在同一条直线上.
设这条直线所对应的函数解析式为:y=kx+b(k≠0),
16.5k+b=115.5
23.1k+b=148.5 ,
得
解得:
k=5
b=33,
∴函数解析式为y=5x+33,
经检验,其余点均在直线y=5x+33上,
∴这些点在同一条直线上,这条直线所对应的函数解析式为y=5x+33;
(2)当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?
解:把y=213代入y=5x+33得:
5x+33=213,
解得x=36,
∴当凳面宽度为213 mm时,以对称轴为基准向两边各取相同的长度为36 mm.
以对称轴为基准向两边各取相同的长度x/mm 16.5 19.8 23.1 26.4 29.7
凳面的宽度y/mm 115.5 132 148.5 165 181.5
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
