2024-2025学年小升初数学备考真题分类汇编(安徽地区专版)专题2 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(安徽地区专版)专题2 填空题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 07:24:46 | ||
图片预览




文档简介
专题2填空题-2023-2024学年
小升初数学备考真题分类汇编(安徽地区专版)
试卷说明:
本试卷试题精选自安徽省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合安徽省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、填空题
1.(2024·固镇县模拟)把一张长32厘米、宽24厘米的长方形纸剪成几个边长相等的正方形,且没有剩余。至少可以剪 个这样的正方形。
2.(2023·怀远)“限塑令”执行后,依诺调查了200名超市顾客。其中有120名顾客自带购物袋,有50名顾客购买超市塑料袋,其余顾客手拿商品没有用袋。如果要统计各种方式所占的百分比,应绘制 统计图,其中自带购物袋的顾客人数占 %。
3.(2023·滁州)人民小学组织防溺水知识竞赛,共20题。评分规则是答对一题得10分,答错一题扣5分。书昱最后得了140分,他答对了 题。
4.(2023·滁州)在横线里填上“>”“<”或“=”。
0.99 3030÷4040 75%
0.01÷99% 0.01
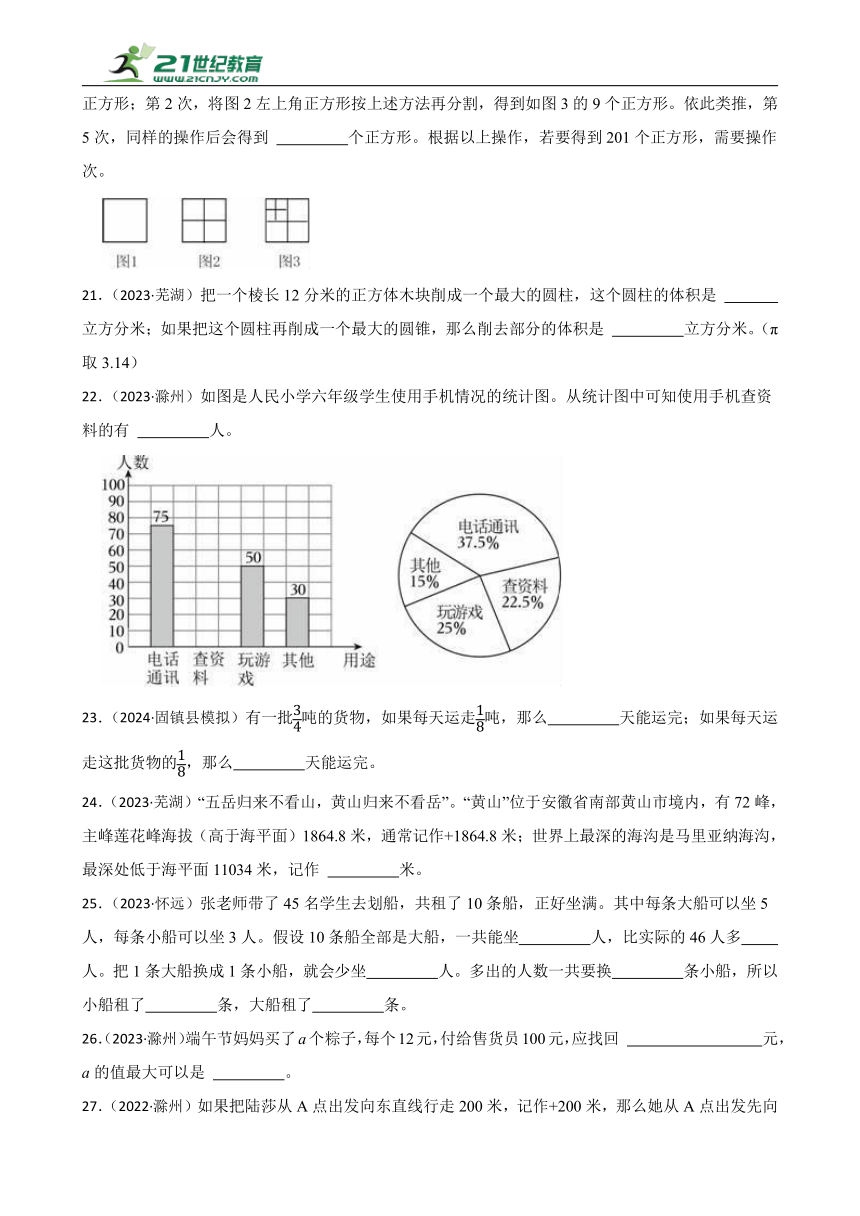
5.(2024·固镇县模拟)坐落于西安市未央区的西安北客站是亚洲最大高铁站之一,西成(西安至成都)高铁就从这里出发,实现了西安人“早上肉夹馍,中午川火锅”的生活梦想。在比例尺为1:10000000的高速铁路线路图上,量得两地的线路长是6.6厘米,两地的实际距离为 千米。
6.(2023·滁州)妈妈的微信钱包里原来有892.53元余额。今天她收到微信红包172元,记作+172元;然后买菜支出92元,记作 元。现在妈妈的微信钱包里还有 元余额。
7.(2023·芜湖)六年级五个班进行篮球友谊赛。六(1)班王同学参加了四场比赛,投篮命中率为50%。已知他在前三场比赛中一共投篮30次,命中率为40%,在第四场比赛中一共投篮10次,那么他在第四场比赛中的投篮命中率是 %。
8.(2024·固镇县模拟)一个长方形的长是6厘米,宽是5厘米。如果以它的长所在的直线为轴旋转一周,就可以得到一个 ,这个立体图形的体积是 立方厘米。
9.(2024·固镇县)
520千克= 吨 15.3平方米= 平方分米 4.25时= 分
10.(2024·固镇县模拟)为参与以环保为主题的“六一”活动,陈铭和闫晨一起制作海洋环保书签,陈铭制作的数量是闫晨的,他们两人制作的总数量在160~170枚之间。陈铭制作了 枚书签,闫晨制作了 枚书签。
11.(2023·滁州)北京时间2023年5月10日21时22分,搭载天舟六号货运飞船的长征七号遥七运载火箭在我国文昌航天发射场点火发射,约10分钟后,天舟六号货运飞船与火箭成功分离并进入预定轨道,之后,飞船太阳能帆板顺利展开工作,发射取得圆满成功。天舟六号货运飞船有一个精密零件长5毫米,画在图纸上是5厘米,这幅图纸的比例尺是 ,从图上量得另一个零件的长度是3.3厘米,它的实际长度是 毫米。
12.(2024·固镇县模拟)某市市民血型比例情况如图,B型血的人数占总人数的 %;如果按这样的比例推算,育才小学是A型血的有232,那么育才小学一共有人 人。
13.(2024·固镇县模拟)一个棱长总和是48厘米的正方体,表面积是 平方厘米,体积是 立方厘米。
14.(2024·固镇县模拟)把2克盐放入48千克水中,盐与水的质量比是 ,含盐率是 %
15.(2024·固镇县模拟)28: == ÷15= %= (填小数)
16.(2024·固镇县模拟)一个数由8个10、6个1、5个0.1和7个0.001组成的,这个数是 ,保留两位小数是 。
17.(2024·固镇县模拟)我们赖以生存的地球,它的表面积约是五亿一千零一十万零九百三十四平方千米,横线上的数写作 ,改写成用“万”作单位的数是 万,省略“亿”后面的尾数约是 亿。
18.(2024·固镇县)六(1)班男生人数比女生人数多,男生人数是女生人数的 ;女生人数是总人数的 ;女生人数比男生人数少 。
19.(2024·固镇县)在横线里填合适的单位。
⑴一瓶矿泉水有555 。 ⑵天安门广场的占地面积约44 。
⑶一昼夜是24 。 ⑷一个鸡蛋约重50 。
20.(2023·滁州)将如图1的正方形进行如下操作:第1次,分别连接对边中点,得到如图2的5个正方形;第2次,将图2左上角正方形按上述方法再分割,得到如图3的9个正方形。依此类推,第5次,同样的操作后会得到 个正方形。根据以上操作,若要得到201个正方形,需要操作 次。
21.(2023·芜湖)把一个棱长12分米的正方体木块削成一个最大的圆柱,这个圆柱的体积是 立方分米;如果把这个圆柱再削成一个最大的圆锥,那么削去部分的体积是 立方分米。(π取3.14)
22.(2023·滁州)如图是人民小学六年级学生使用手机情况的统计图。从统计图中可知使用手机查资料的有 人。
23.(2024·固镇县模拟)有一批吨的货物,如果每天运走吨,那么 天能运完;如果每天运走这批货物的,那么 天能运完。
24.(2023·芜湖)“五岳归来不看山,黄山归来不看岳”。“黄山”位于安徽省南部黄山市境内,有72峰,主峰莲花峰海拔(高于海平面)1864.8米,通常记作+1864.8米;世界上最深的海沟是马里亚纳海沟,最深处低于海平面11034米,记作 米。
25.(2023·怀远)张老师带了45名学生去划船,共租了10条船,正好坐满。其中每条大船可以坐5人,每条小船可以坐3人。假设10条船全部是大船,一共能坐 人,比实际的46人多 人。把1条大船换成1条小船,就会少坐 人。多出的人数一共要换 条小船,所以小船租了 条,大船租了 条。
26.(2023·滁州)端午节妈妈买了a个粽子,每个12元,付给售货员100元,应找回 元,a的值最大可以是 。
27.(2022·滁州)如果把陆莎从A点出发向东直线行走200米,记作+200米,那么她从A点出发先向东直线行走360米,再沿原路向西直线行走480米,最后她走的路程可记作 米。
28.(2023·滁州)如图所示,把一个棱长是12分米的正方体木料削成个最大的圆柱,圆柱的体积是 立方分米;再把该圆柱削成一个最大的圆锥,还要再削去 立方分米。
29.(2023·滁州)0.6m2= dm2
9090毫升= 升
3时20分= 时
30.(2023·怀远)三角形的底是16厘米,高是12厘米,把它按 的比缩小后,底是4厘米,高是 厘米。
31.(2021·博罗)15和20的最大公因数是 ,最小公倍数是 。
32.(2023·芜湖)一只甲虫从A地出发,先向西偏南30°方向爬了45cm到达B地;接着由B地出发向东偏北30°方向爬了60cm到达C地,这时甲虫离A地 cm。
33.(2023·芜湖)30: == ÷30= %= 折
34.(2023·芜湖)如图,将一个边长为1的正方形纸片分割成7部分,部分②是部分①面积的一半,部分③是部分②面积的一半……以此类推。
(1)阴影部分的面积是 。
(2)计算:= 。
35.(2023·芜湖)如果某图纸用的比例尺是40:1,一个零件图上的长度是8厘米,它实际长度是 毫米;在的图纸上量得一个正方形的面积为16平方厘米,它的实际面积是 平方米。
36.(2023·芜湖)把1米长的长方体木料沿横截面锯成两段,这两段木料的表面积之和比原木料的表面积增加了60平方厘米。原来这根木料的体积是 立方厘米。
37.(2023·芜湖)一根绳子全长a米,如果用去米,还剩 米;如果用去全长的,还剩 m。
38.(2023·怀远)一个直角三角形的三条边分别是13厘米、12厘米、5厘米,它的面积是 平方厘米;以它的两条直角边所在的直线各旋转一周,得到两个不同的 ,它们的体积相差 立方厘米。
39.(2023·滁州)30: = =3÷5= %= 成= (最后一空填小数)。
40.(2023·芜湖)在一道减法算式中,被减数,减数与差的和是360,差是减数的,差是 ,减数是 。
41.(2023·芜湖)一个等腰三角形中两个内角的比是1:4,这个等腰三角形的顶角可能是 度。
42.(2023·滁州)一根绳子如果剪去它的,还剩4米,这根绳子原来长 米;如果这根绳子剪去米,还剩 米。
43.(2023·芜湖)六(1)班有男生20人,女生25人,那么女生比男生多 %,男生比女生少 %。
44.(2024·固镇县模拟)全班38名人去划船,共租了12条船正好坐满。每条大船可以坐5人,每条小船可以坐3人。租了 条小船。
45.(2023·芜湖)农谚“逢冬数九”讲的是从冬至之日起,每九天分为一段,依次称之为一九,二九,……,九九。冬至那天是一九的第一天,2022年12月22日是冬至,那么2023年的春节1月22日是 九的第 天。
46.(2023·怀远)一个圆柱的侧面积是37.68平方厘米,底面半径是2厘米,这个圆柱的体积是 立方厘米。
47.(2023·芜湖)中国是世界上水土流失最为严重的国家之一。据最新资料显示,每年流失的土壤总量达4998000000吨,横线上的数读作 ,改写成以亿作单位并保留一位小数约是 亿。
48.(2023·怀远)在阳光下,同一时间、同一地点物体的高度和影长成 比例。如果某一刻一根竹竿高3米,影长2米,同一时刻、同一地点一幢教学楼的影长是12.6米,那么教学楼高 米。
49.(2023·怀远)参加研学的男生和女生的人数比是5:6,男、女生人数之和在80~90之间,参加研学的男生有 人,女生有 人。
50.(2023·怀远)做一项工作,师傅单独完成需要2小时,徒弟单独完成需要2.5小时,师傅的工作效率比徒弟高 %。
答案解析部分
1.12
解:32和24的最大公因数是2×2×2=8
(32÷8)×(24÷8)
=4×3
=12(个)。
故答案为:12。
至少可以剪这样正方形的个数=长边剪的个数×宽边剪的个数,其中,长、宽边分别剪的个数=长、宽÷32和24的最大公因数。
2.扇形;60
解:“限塑令”执行后,依诺调查了200名超市顾客。其中有120名顾客自带购物袋,有50名顾客购买超市塑料袋,其余顾客手拿商品没有用袋。如果要统计各种方式所占的百分比,应绘制扇形统计图,其中自带购物袋的顾客人数占120÷200=60%。
故答案为:扇形;60。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。用自带购物袋的人数除以总人数即可求出自带购物袋的顾客人数占总人数的百分率。
3.16
解:假设他答对了x题,则答错了(20-x)题。
10x-5(20-x)=140
10x-100+5x=140
15x=140+100
15x=240
x=240÷15
x=16
故答案为:16。
答对题的得分-答错题倒扣的分=最后得分,据此等量关系列方程,根据等式性质解方程。
4.<;=;>;>
解:<1,所以<0.99
3030÷4040 =0.75=75%
99%<1,所以0.01÷99% >0.01
>,<,所以 >
故答案为:<;=;>;>。
一个非0数乘大于1的数,积大于这个数,乘小于1的数,积小于这个数;
一个非0数除以大于1的数,商小于这个数,除以小于1的数,商大于这个数。
5.660
解:6.6÷÷100000
=66000000÷100000
=660(千米)。
故答案为:660。
两地的实际距离=图上距离÷比例尺,然后单位换算。
6.﹣92;972.53
解:买菜支出92元,记作-92元;
892.53+172-92=972.53(元),现在妈妈的微信钱包里还有972.53元余额。
故答案为:-92;972.53。
第一空:收入为正,支出为负;
第二空:妈妈的微信钱包里原来的钱数+收入的钱数-支出的钱数=现在的钱数。
7.80
解:(10+30)×50%
=40×50%
=20(次)
30×40%=12(次)
(20-12)÷10
=8÷10
=80%。
故答案为:80。
根据四场比赛投篮命中率为50%;共投篮10+30=40次,再根据分数的意义求出前三场命中的次数,即可求出第四场命中的次数,再用第四场命中的次数÷10,就是第四场比赛的命中率。
8.圆柱体;471
解:如果以它的长所在的直线为轴旋转一周,就可以得到一个圆柱体;
3.14×52×6
=78.5×6
=471(立方厘米)。
故答案为:圆柱体;471。
如果以它的长所在的直线为轴旋转一周,就可以得到一个圆柱体;
这个圆柱的体积=π×半径2×高。
9.0.52;1530;255
解:520÷1000=0.52(吨);
15.3×100=1530(平方分米);
4.25×60=255(分)。
故答案为:0.52;1530;255。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
10.36;126
解:设闫晨制作了x个海洋环保书签,则陈铭制作了x个海洋环保书签。
x+x=x,x在160~170之间 ,为整数,并且x是整数,所以,
x=162
x=162÷
x=126
126×=36(枚)。
故答案为:36;126。
设闫晨制作了x个海洋环保书签,则陈铭制作了x个海洋环保书签。然后把他们两个做的个数相加等于x在160~170之间 ,为整数,并且x是整数,所以,x=162,求出x=126。
11.10:1;3.3
解:图纸距离5厘米,实际距离5毫米,比例尺5厘米:5毫米=50毫米:5毫米=10:1;
3.3厘米÷=0.33厘米=3.3毫米,它的实际长度是3.3毫米。
故答案为:10:1;3.3。
第一空:一幅图的图上距离与实际距离的比,叫做这幅图的比例尺;求比例尺时,单位不统一的先统一单位,再把比写成前项或后项是1的形式;
第二空:实际距离=图上距离÷比例尺。
12.40;928
解:1-25%-22.5%-12.5%
=75%-22.5%-12.5%
=52.5%-12.5%
=40%;
232÷25%=928(人)。
故答案为:40;928。
B型血的人数占总人数的百分率=单位“1” -其余各项分别占的百分率;育才小学一共的人数=A型血的人数÷所占的百分率。
13.96;64
解:48÷12=4(厘米)
4×4×6
=16×6
=96(平方厘米)
4×4×4
=16×4
=64(立方厘米)。
故答案为:96;64。
正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长;其中,棱长=棱长和÷12。
14.1:24000;0.0044%
解:2:(48×1000)=1:24000;
1÷(1+24000)
=1÷24001
≈0.0044%。
故答案为:1:24000;0.0044%。
盐与水的质量比=盐的质量:水的质量,关键是单位换算;含盐率=盐的质量÷(盐的质量+水的质量)。
15.35;12;80;0.8
解:28÷=35;
×15=12;
=4÷5=0.8=80%;
所以28:35==12÷15=80%=0.8。
故答案为:35;12;80;0.8。
比的后项=比的前项÷比值;被除数=商×除数;分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号。
16.86.507;86.51
解:由8个10、6个1、5个0.1和7个0.001组成的数是86.507;
86.507≈86.51。
故答案为:86.507;86.51。
小数点的左边是整数部分,表示几个一,小数点右边第一位是十分位,表示几个0.1,小数点右边第二位是百分位,表示几个0.01,小数点右边第三位是千分位,表示几个0.001······;
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
17.510100934;51010.0934;5
解:五亿一千零一十万零九百三十四写作:510100934;
510100934÷10000=51010.0934万;
51010.0934万≈5亿。
故答案为:510100934;51010.0934;5。
亿以上的数的写法,先看这个数有几级,再从最高级写起,哪个数位上一个单位也没有,就在那个数位上写0;
改写成用“万”作单位的数,小数点向左移动4位,再在后面加上一个“万”字;
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
18.;;
解:(1+4)÷4
=5÷4
=
4÷(4+5)
=4÷9
=
(5-4)÷5
=1÷5
=。
故答案为:;;。
把女生人数看作4份,男生是4+1=5份,男生人数是女生人数的分率=男生人数÷女生人数;
女生人数是总人数的分率=女生人数÷(男生人数+女生人数);女生人数比男生人数少的分率=(男生人数-女生人数)÷男生人数。
19.毫升;公顷;小时;克
解:
⑴一瓶矿泉水有555毫升; ⑵天安门广场的占地面积约44公顷;
⑶一昼夜是24小时; ⑷一个鸡蛋约重50克。
故答案为:(1)毫升;(2)公顷;(3)小时;(4)克。
根据实际生活经验以及题干中的具体数据来进行填空。
20.21;50
解:第1次:分别连接各边中点如图2,得到4×1+1=5个正方形;
第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9个正方形;
…...,
第5次:得到4×5+1=21个正方形;
以此类推,根据以上操作,则第n次得到4n+1个正方形,
4n+1=201
4n=200
n=50
若要得到201个正方形,需要操作50次。
故答案为:21;50。
第一空:根据题干的内容,找出本题的规律,并用关系式总结出来;
第二空:把201代入关系式中进行解答。
21.1356.48;904.32
解:12÷2=6(分米)
3.14×62×12
=113.04×12
=1356.48(立方分米)
1356.48×=904.32(立方分米)。
故答案为:1356.48;904.32。
这个圆柱的体积=π×半径2×高; 其中,高=直径=正方体的棱长;削去部分的体积=这个圆柱的体积×。
22.45
解:50÷25%=200(人)
200×22.5%=45(人)
故答案为:45。
玩游戏的人数÷玩游戏的人数占总人数的百分率=总人数,总人数×查资料的人数占总人数的百分率=查资料的人数。
23.6;8
解:÷=6(天);
1÷=8(天)。
故答案为:6;8。
每天运的质量=这批货物的总质量÷平均每天运的质量;运完需要的天数=1÷平均每天运的分率。
24.-11034
解:低于海平面11034米,记作:-11034米。
故答案为:-11034。
正数和负数表示具有相反意义的量,高于海平面的记作正数,低于海平面的记作负数。
25.50;4;2;2;2;8
解:张老师带了45名学生去划船,共租了10条船,正好坐满。其中每条大船可以坐5人,每条小船可以坐3人。假设10条船全部是大船,一共能坐10×5=50人,比实际的46人多4人。把1条大船换成1条小船,就会少坐5-3=2人。多出的人数一共要换4÷2=2条小船,所以小船租了2条,大船租了10-2=8条。
故答案为:50;4;2;2;2;8。
假设全部都是大船,则共可以坐50人,比46人多4人,是因为把小船也当作坐5人来计算了,这样每条小船多算了2人,因此用一共多算的人数除以每条小船多算的人数即可求出小船的条数,进而求出大船的条数。
26.(100﹣12a);8
解:买粽子花的钱数:12a元,
应找回的钱数:(100-12a)元,
12a=100,
a=100÷12,
a=8......4
a的值最大可以是8。
故答案为:(100﹣12a);8。
第一空:每个粽子的钱数×12=买粽子花的钱数,付给售货员的钱数-买粽子花的钱数=应找回的钱数;
第二空:买粽子花的钱数小于或等于付给售货员的钱数,据此求出a的最大值。
27.-120
解:如果把陆莎从A点出发向东直线行走200米,记作+200米,那么她从A点出发先向东直线行走360米,再沿原路向西直线行走480米,最后她走的路程可记作-120米。
故答案为:-120。
正负数表示相反意义的量,向东记作正,那么向西就记作负。先向东直线行走360米,再沿原路向西直线行走480米,相当于向西走了120米,所以记作-120米。
28.1356.48;904.32
解:圆柱的底面直径是12分米,底面半径是6分米,高是12分米,
圆柱的体积:3.14×6×6×12=113.04×12=1356.48(立方分米)
圆锥的体积:1356.48×=904.32(立方分米)
故答案为:1356.48;904.32。
圆柱的体积=π×底面半径的平方×高,削去的体积=圆柱的体积×。
29.60;9.09;
解:0.6×100=60,所以0.6平方米=60平方分米,
9090÷1000=9.09,所以9090毫升=9.09升,
20分÷60=时,所以3时20分=小时。
故答案为:60;9.09;。
1平方米=100平方分米,1升=1000毫升,1时=60分;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
30.1:4;3
解:16÷4=4,所以是按照1:4的比缩小,高是12÷4=3(厘米)。
故答案为:1:4;3。
用原来的底除以现在的底求出底缩小的倍数,然后写出缩小后底与原来底的比即可求出缩小的比,然后把高也缩小相同的倍数求出现在的高。
31.5;60
解:
15和20的最大公因数是:5,最小公倍数是:
5×3×4
=15×4
=60
故答案为:5;60。
根据题意可知求两个数的最大公因数和最小公倍数,用短除法,依次除以这两数公有的质因数,直到最后两个数是互质数为止。
32.15
解:60-45=15(厘米)。
故答案为:15。
甲虫从A地出发,先向西偏南30°方向爬了45厘米到达B地,然后又原路返回爬了60厘米,则 这时甲虫离A地的距离=60-45=15厘米。
33.50;18;60;六
解:=(3×10):(5×10)=30:50;
=(3×6)÷(5×6)=18÷30;
=3÷5=0.6=60%=六折;
所以30:50==18÷30=60%=六折。
故答案为:50;18;60;六。
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就等于几成;百分之几十就是几折;比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
34.(1)
(2)
解:(1)×××××
=××××
=×××
=××
=×
=;
(2)
=(1-)+(-)+(-)+···+(-)
=1-+-+-++···-
=1-
=。
故答案为:;。
(1)观察发现①的面积是,②的面积是=······,n的面积是2的n次方分之一,据此计算;
(2)=1-=。
35.2;1600
解:8×10÷40
=80÷40
=2(毫米)
16÷4=4(厘米)
4÷÷100
=4÷÷100
=4000÷100
=40(米)
40×40=1600(平方米)。
故答案为:2;1600。
实际距离=图上距离÷比例尺;正方形的边长×正方形的边长=面积,求出正方形的边长=4厘米,然后求出实际距离,依据正方形的面积公式求出面积。
36.3000
解:1米=100厘米
60÷2×100
=30×100
=3000(立方厘米)。
故答案为:3000。
原来这根木料的体积=横截面的面积×长方体木料原来的长度;其中,横截面的面积=增加的表面积÷2。
37.(a-);a
解:a-=(a-)(米);
a-a=a(米)。
故答案为:(a-);a。
用去米,还剩下的米数=这根绳子的总米数-用去的米数; 用去,还剩下的米数=这根绳子的总米数-这根绳子的总米数×用去的分率。
38.30;圆锥;439.6
解:面积:12×5÷2=30(平方厘米);
以它的两条直角边所在的直线各旋转一周,得到两个不同的圆锥,它们的体积相差:
3.14×122×5×-3.14×52×12×
=3.14×240-3.14×100
=3.14×140
=439.6(立方厘米)
故答案为:30;圆锥;439.6。
三角形中斜边最长,因此两条较短的边就是三角形的两条直角边,根据三角形面积公式计算面积。以三角形的一条直角边为轴旋转一周会得到一个圆锥,为轴的那条直角边是圆锥的高,另一条直角边就是圆锥的底面半径,计算出两个圆锥的体积,相减后就是体积相差的部分。
39.50;18;60;六;0.6
解:3÷5=3:5==0.6=60%=六成,
3:5=30:50;=。
故答案为:50;18;60;六;0.6。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
比的基本性质:比的前项和后项同时乘或除以(0除外)相同的数,比值不变;
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;
成数表示一个数是另一个数的十分之几,统称几成。
40.30;150
解:(360÷2)÷(1+)
=180÷
=150
180-150=30。
故答案为:30;150。
差+减数=被减数=360÷2=180,减数=180÷(1+)=150,差=180-150=30。
41.20或120
解:180°÷(1+4+4)×1
=180°÷9
=20°;
180°÷(1+1+4)×4
=180°÷6×4
=30°×4
=120°。
故答案为:20或120。
①这个等腰三角形顶角的度数=三角形的内角和÷总份数×顶角占的份数×顶角占的份数;②这个等腰三角形顶角的度数=三角形的内角和÷总份数×顶角占的份数。
42.7;
解:4÷(1-)=4÷=7(米)
7-=6(米)
故答案为:7;6。
第一空:剩下的长度÷剩下的长度占全长的几分之几=这根绳子原来长;
第二空:这根绳子原来长-剪去的长度=还剩的长度。
43.25;20
解:(25-20)÷20
=5÷20
=25%
(25-20)÷25
=5÷25
=20%。
故答案为:25;20。
女生比男生多的百分率=(男生人数-女生人数)÷男生人数;男生比女生少的百分率=(男生人数-女生人数)÷女生人数。
44.11
解:假设全部租的大船,则租小船的条数:
(12×5-38)÷(5-3)
=22÷2
=11(条)。
故答案为:11。
假设全部租的大船,则租小船的条数=(平均每条大船限乘的人数×总条数-去划船的总人数)平均每条大船限乘的人数÷(平均每条大船限乘的人数-平均每条小船限乘的人数)。
45.四;5
解:(31-22+1+22)÷9
=32÷9
=3······5,则是四九的第5天。
故答案为:四;5。
从2022年12月22日~2023年1月22日经过的天数=(12月的天数-22天+1天+22天) =32天,32天里有3个9还剩下5天,所以是四九的第5天。
46.37.68
解:高:37.68÷(3.14×2×2)=37.68÷12.56=3(厘米);
体积:3.14×22×3=37.68(平方厘米)。
故答案为:37.68。
用圆柱的侧面积除以底面周长即可求出圆柱的高,然后用圆柱的底面积乘高即可求出圆柱的体积。
47.四十九亿九千八百万;50.0
解:4998000000读作:四十九亿九千八百万;
4998000000≈50.0亿。
故答案为:四十九亿九千八百万;50.0。
亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零;用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
48.正;18.9
解:在阳光下,同一时间、同一地点物体的高度和影长成正比例。如果某一刻一根竹竿高3米,影长2米,同一时刻、同一地点一幢教学楼的影长是12.6米,那么教学楼高:12.6×(3÷2)=18.9米。
故答案为:正;18.9。
同一时间、同一地点物体的高度和影长的比值是不变的,二者成正比例。竹竿高3米,影长2米,用3除以2求出竹竿是影长的几倍,然后把教学楼的影长乘这个倍数即可求出教学楼的高度。
49.40;48
解:5+6=11,80~90之间11的倍数是88,所以总人数的88人;
88÷11=8(人)
男生:8×5=40(人)
女生:8×6=48(人)
故答案为:40;48。
男生和女生的总份数是11,根据人数的特殊性,总人数一定是11的倍数,因此找出80~90之间11的倍数就是总人数。用总人数除以总份数求出每份数,然后分别求出男生和女生的人数。
50.25
解:(-)÷
=×
=25%
故答案为:25。
把这项工作看作单位“1”,用分数分别表示处两人的工作效率,用两人的工作效率差除以徒弟的工作效率即可求出师傅的工作效率比徒弟的工作效率多百分之几。
小升初数学备考真题分类汇编(安徽地区专版)
试卷说明:
本试卷试题精选自安徽省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合安徽省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、填空题
1.(2024·固镇县模拟)把一张长32厘米、宽24厘米的长方形纸剪成几个边长相等的正方形,且没有剩余。至少可以剪 个这样的正方形。
2.(2023·怀远)“限塑令”执行后,依诺调查了200名超市顾客。其中有120名顾客自带购物袋,有50名顾客购买超市塑料袋,其余顾客手拿商品没有用袋。如果要统计各种方式所占的百分比,应绘制 统计图,其中自带购物袋的顾客人数占 %。
3.(2023·滁州)人民小学组织防溺水知识竞赛,共20题。评分规则是答对一题得10分,答错一题扣5分。书昱最后得了140分,他答对了 题。
4.(2023·滁州)在横线里填上“>”“<”或“=”。
0.99 3030÷4040 75%
0.01÷99% 0.01
5.(2024·固镇县模拟)坐落于西安市未央区的西安北客站是亚洲最大高铁站之一,西成(西安至成都)高铁就从这里出发,实现了西安人“早上肉夹馍,中午川火锅”的生活梦想。在比例尺为1:10000000的高速铁路线路图上,量得两地的线路长是6.6厘米,两地的实际距离为 千米。
6.(2023·滁州)妈妈的微信钱包里原来有892.53元余额。今天她收到微信红包172元,记作+172元;然后买菜支出92元,记作 元。现在妈妈的微信钱包里还有 元余额。
7.(2023·芜湖)六年级五个班进行篮球友谊赛。六(1)班王同学参加了四场比赛,投篮命中率为50%。已知他在前三场比赛中一共投篮30次,命中率为40%,在第四场比赛中一共投篮10次,那么他在第四场比赛中的投篮命中率是 %。
8.(2024·固镇县模拟)一个长方形的长是6厘米,宽是5厘米。如果以它的长所在的直线为轴旋转一周,就可以得到一个 ,这个立体图形的体积是 立方厘米。
9.(2024·固镇县)
520千克= 吨 15.3平方米= 平方分米 4.25时= 分
10.(2024·固镇县模拟)为参与以环保为主题的“六一”活动,陈铭和闫晨一起制作海洋环保书签,陈铭制作的数量是闫晨的,他们两人制作的总数量在160~170枚之间。陈铭制作了 枚书签,闫晨制作了 枚书签。
11.(2023·滁州)北京时间2023年5月10日21时22分,搭载天舟六号货运飞船的长征七号遥七运载火箭在我国文昌航天发射场点火发射,约10分钟后,天舟六号货运飞船与火箭成功分离并进入预定轨道,之后,飞船太阳能帆板顺利展开工作,发射取得圆满成功。天舟六号货运飞船有一个精密零件长5毫米,画在图纸上是5厘米,这幅图纸的比例尺是 ,从图上量得另一个零件的长度是3.3厘米,它的实际长度是 毫米。
12.(2024·固镇县模拟)某市市民血型比例情况如图,B型血的人数占总人数的 %;如果按这样的比例推算,育才小学是A型血的有232,那么育才小学一共有人 人。
13.(2024·固镇县模拟)一个棱长总和是48厘米的正方体,表面积是 平方厘米,体积是 立方厘米。
14.(2024·固镇县模拟)把2克盐放入48千克水中,盐与水的质量比是 ,含盐率是 %
15.(2024·固镇县模拟)28: == ÷15= %= (填小数)
16.(2024·固镇县模拟)一个数由8个10、6个1、5个0.1和7个0.001组成的,这个数是 ,保留两位小数是 。
17.(2024·固镇县模拟)我们赖以生存的地球,它的表面积约是五亿一千零一十万零九百三十四平方千米,横线上的数写作 ,改写成用“万”作单位的数是 万,省略“亿”后面的尾数约是 亿。
18.(2024·固镇县)六(1)班男生人数比女生人数多,男生人数是女生人数的 ;女生人数是总人数的 ;女生人数比男生人数少 。
19.(2024·固镇县)在横线里填合适的单位。
⑴一瓶矿泉水有555 。 ⑵天安门广场的占地面积约44 。
⑶一昼夜是24 。 ⑷一个鸡蛋约重50 。
20.(2023·滁州)将如图1的正方形进行如下操作:第1次,分别连接对边中点,得到如图2的5个正方形;第2次,将图2左上角正方形按上述方法再分割,得到如图3的9个正方形。依此类推,第5次,同样的操作后会得到 个正方形。根据以上操作,若要得到201个正方形,需要操作 次。
21.(2023·芜湖)把一个棱长12分米的正方体木块削成一个最大的圆柱,这个圆柱的体积是 立方分米;如果把这个圆柱再削成一个最大的圆锥,那么削去部分的体积是 立方分米。(π取3.14)
22.(2023·滁州)如图是人民小学六年级学生使用手机情况的统计图。从统计图中可知使用手机查资料的有 人。
23.(2024·固镇县模拟)有一批吨的货物,如果每天运走吨,那么 天能运完;如果每天运走这批货物的,那么 天能运完。
24.(2023·芜湖)“五岳归来不看山,黄山归来不看岳”。“黄山”位于安徽省南部黄山市境内,有72峰,主峰莲花峰海拔(高于海平面)1864.8米,通常记作+1864.8米;世界上最深的海沟是马里亚纳海沟,最深处低于海平面11034米,记作 米。
25.(2023·怀远)张老师带了45名学生去划船,共租了10条船,正好坐满。其中每条大船可以坐5人,每条小船可以坐3人。假设10条船全部是大船,一共能坐 人,比实际的46人多 人。把1条大船换成1条小船,就会少坐 人。多出的人数一共要换 条小船,所以小船租了 条,大船租了 条。
26.(2023·滁州)端午节妈妈买了a个粽子,每个12元,付给售货员100元,应找回 元,a的值最大可以是 。
27.(2022·滁州)如果把陆莎从A点出发向东直线行走200米,记作+200米,那么她从A点出发先向东直线行走360米,再沿原路向西直线行走480米,最后她走的路程可记作 米。
28.(2023·滁州)如图所示,把一个棱长是12分米的正方体木料削成个最大的圆柱,圆柱的体积是 立方分米;再把该圆柱削成一个最大的圆锥,还要再削去 立方分米。
29.(2023·滁州)0.6m2= dm2
9090毫升= 升
3时20分= 时
30.(2023·怀远)三角形的底是16厘米,高是12厘米,把它按 的比缩小后,底是4厘米,高是 厘米。
31.(2021·博罗)15和20的最大公因数是 ,最小公倍数是 。
32.(2023·芜湖)一只甲虫从A地出发,先向西偏南30°方向爬了45cm到达B地;接着由B地出发向东偏北30°方向爬了60cm到达C地,这时甲虫离A地 cm。
33.(2023·芜湖)30: == ÷30= %= 折
34.(2023·芜湖)如图,将一个边长为1的正方形纸片分割成7部分,部分②是部分①面积的一半,部分③是部分②面积的一半……以此类推。
(1)阴影部分的面积是 。
(2)计算:= 。
35.(2023·芜湖)如果某图纸用的比例尺是40:1,一个零件图上的长度是8厘米,它实际长度是 毫米;在的图纸上量得一个正方形的面积为16平方厘米,它的实际面积是 平方米。
36.(2023·芜湖)把1米长的长方体木料沿横截面锯成两段,这两段木料的表面积之和比原木料的表面积增加了60平方厘米。原来这根木料的体积是 立方厘米。
37.(2023·芜湖)一根绳子全长a米,如果用去米,还剩 米;如果用去全长的,还剩 m。
38.(2023·怀远)一个直角三角形的三条边分别是13厘米、12厘米、5厘米,它的面积是 平方厘米;以它的两条直角边所在的直线各旋转一周,得到两个不同的 ,它们的体积相差 立方厘米。
39.(2023·滁州)30: = =3÷5= %= 成= (最后一空填小数)。
40.(2023·芜湖)在一道减法算式中,被减数,减数与差的和是360,差是减数的,差是 ,减数是 。
41.(2023·芜湖)一个等腰三角形中两个内角的比是1:4,这个等腰三角形的顶角可能是 度。
42.(2023·滁州)一根绳子如果剪去它的,还剩4米,这根绳子原来长 米;如果这根绳子剪去米,还剩 米。
43.(2023·芜湖)六(1)班有男生20人,女生25人,那么女生比男生多 %,男生比女生少 %。
44.(2024·固镇县模拟)全班38名人去划船,共租了12条船正好坐满。每条大船可以坐5人,每条小船可以坐3人。租了 条小船。
45.(2023·芜湖)农谚“逢冬数九”讲的是从冬至之日起,每九天分为一段,依次称之为一九,二九,……,九九。冬至那天是一九的第一天,2022年12月22日是冬至,那么2023年的春节1月22日是 九的第 天。
46.(2023·怀远)一个圆柱的侧面积是37.68平方厘米,底面半径是2厘米,这个圆柱的体积是 立方厘米。
47.(2023·芜湖)中国是世界上水土流失最为严重的国家之一。据最新资料显示,每年流失的土壤总量达4998000000吨,横线上的数读作 ,改写成以亿作单位并保留一位小数约是 亿。
48.(2023·怀远)在阳光下,同一时间、同一地点物体的高度和影长成 比例。如果某一刻一根竹竿高3米,影长2米,同一时刻、同一地点一幢教学楼的影长是12.6米,那么教学楼高 米。
49.(2023·怀远)参加研学的男生和女生的人数比是5:6,男、女生人数之和在80~90之间,参加研学的男生有 人,女生有 人。
50.(2023·怀远)做一项工作,师傅单独完成需要2小时,徒弟单独完成需要2.5小时,师傅的工作效率比徒弟高 %。
答案解析部分
1.12
解:32和24的最大公因数是2×2×2=8
(32÷8)×(24÷8)
=4×3
=12(个)。
故答案为:12。
至少可以剪这样正方形的个数=长边剪的个数×宽边剪的个数,其中,长、宽边分别剪的个数=长、宽÷32和24的最大公因数。
2.扇形;60
解:“限塑令”执行后,依诺调查了200名超市顾客。其中有120名顾客自带购物袋,有50名顾客购买超市塑料袋,其余顾客手拿商品没有用袋。如果要统计各种方式所占的百分比,应绘制扇形统计图,其中自带购物袋的顾客人数占120÷200=60%。
故答案为:扇形;60。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。用自带购物袋的人数除以总人数即可求出自带购物袋的顾客人数占总人数的百分率。
3.16
解:假设他答对了x题,则答错了(20-x)题。
10x-5(20-x)=140
10x-100+5x=140
15x=140+100
15x=240
x=240÷15
x=16
故答案为:16。
答对题的得分-答错题倒扣的分=最后得分,据此等量关系列方程,根据等式性质解方程。
4.<;=;>;>
解:<1,所以<0.99
3030÷4040 =0.75=75%
99%<1,所以0.01÷99% >0.01
>,<,所以 >
故答案为:<;=;>;>。
一个非0数乘大于1的数,积大于这个数,乘小于1的数,积小于这个数;
一个非0数除以大于1的数,商小于这个数,除以小于1的数,商大于这个数。
5.660
解:6.6÷÷100000
=66000000÷100000
=660(千米)。
故答案为:660。
两地的实际距离=图上距离÷比例尺,然后单位换算。
6.﹣92;972.53
解:买菜支出92元,记作-92元;
892.53+172-92=972.53(元),现在妈妈的微信钱包里还有972.53元余额。
故答案为:-92;972.53。
第一空:收入为正,支出为负;
第二空:妈妈的微信钱包里原来的钱数+收入的钱数-支出的钱数=现在的钱数。
7.80
解:(10+30)×50%
=40×50%
=20(次)
30×40%=12(次)
(20-12)÷10
=8÷10
=80%。
故答案为:80。
根据四场比赛投篮命中率为50%;共投篮10+30=40次,再根据分数的意义求出前三场命中的次数,即可求出第四场命中的次数,再用第四场命中的次数÷10,就是第四场比赛的命中率。
8.圆柱体;471
解:如果以它的长所在的直线为轴旋转一周,就可以得到一个圆柱体;
3.14×52×6
=78.5×6
=471(立方厘米)。
故答案为:圆柱体;471。
如果以它的长所在的直线为轴旋转一周,就可以得到一个圆柱体;
这个圆柱的体积=π×半径2×高。
9.0.52;1530;255
解:520÷1000=0.52(吨);
15.3×100=1530(平方分米);
4.25×60=255(分)。
故答案为:0.52;1530;255。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
10.36;126
解:设闫晨制作了x个海洋环保书签,则陈铭制作了x个海洋环保书签。
x+x=x,x在160~170之间 ,为整数,并且x是整数,所以,
x=162
x=162÷
x=126
126×=36(枚)。
故答案为:36;126。
设闫晨制作了x个海洋环保书签,则陈铭制作了x个海洋环保书签。然后把他们两个做的个数相加等于x在160~170之间 ,为整数,并且x是整数,所以,x=162,求出x=126。
11.10:1;3.3
解:图纸距离5厘米,实际距离5毫米,比例尺5厘米:5毫米=50毫米:5毫米=10:1;
3.3厘米÷=0.33厘米=3.3毫米,它的实际长度是3.3毫米。
故答案为:10:1;3.3。
第一空:一幅图的图上距离与实际距离的比,叫做这幅图的比例尺;求比例尺时,单位不统一的先统一单位,再把比写成前项或后项是1的形式;
第二空:实际距离=图上距离÷比例尺。
12.40;928
解:1-25%-22.5%-12.5%
=75%-22.5%-12.5%
=52.5%-12.5%
=40%;
232÷25%=928(人)。
故答案为:40;928。
B型血的人数占总人数的百分率=单位“1” -其余各项分别占的百分率;育才小学一共的人数=A型血的人数÷所占的百分率。
13.96;64
解:48÷12=4(厘米)
4×4×6
=16×6
=96(平方厘米)
4×4×4
=16×4
=64(立方厘米)。
故答案为:96;64。
正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长;其中,棱长=棱长和÷12。
14.1:24000;0.0044%
解:2:(48×1000)=1:24000;
1÷(1+24000)
=1÷24001
≈0.0044%。
故答案为:1:24000;0.0044%。
盐与水的质量比=盐的质量:水的质量,关键是单位换算;含盐率=盐的质量÷(盐的质量+水的质量)。
15.35;12;80;0.8
解:28÷=35;
×15=12;
=4÷5=0.8=80%;
所以28:35==12÷15=80%=0.8。
故答案为:35;12;80;0.8。
比的后项=比的前项÷比值;被除数=商×除数;分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号。
16.86.507;86.51
解:由8个10、6个1、5个0.1和7个0.001组成的数是86.507;
86.507≈86.51。
故答案为:86.507;86.51。
小数点的左边是整数部分,表示几个一,小数点右边第一位是十分位,表示几个0.1,小数点右边第二位是百分位,表示几个0.01,小数点右边第三位是千分位,表示几个0.001······;
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
17.510100934;51010.0934;5
解:五亿一千零一十万零九百三十四写作:510100934;
510100934÷10000=51010.0934万;
51010.0934万≈5亿。
故答案为:510100934;51010.0934;5。
亿以上的数的写法,先看这个数有几级,再从最高级写起,哪个数位上一个单位也没有,就在那个数位上写0;
改写成用“万”作单位的数,小数点向左移动4位,再在后面加上一个“万”字;
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
18.;;
解:(1+4)÷4
=5÷4
=
4÷(4+5)
=4÷9
=
(5-4)÷5
=1÷5
=。
故答案为:;;。
把女生人数看作4份,男生是4+1=5份,男生人数是女生人数的分率=男生人数÷女生人数;
女生人数是总人数的分率=女生人数÷(男生人数+女生人数);女生人数比男生人数少的分率=(男生人数-女生人数)÷男生人数。
19.毫升;公顷;小时;克
解:
⑴一瓶矿泉水有555毫升; ⑵天安门广场的占地面积约44公顷;
⑶一昼夜是24小时; ⑷一个鸡蛋约重50克。
故答案为:(1)毫升;(2)公顷;(3)小时;(4)克。
根据实际生活经验以及题干中的具体数据来进行填空。
20.21;50
解:第1次:分别连接各边中点如图2,得到4×1+1=5个正方形;
第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9个正方形;
…...,
第5次:得到4×5+1=21个正方形;
以此类推,根据以上操作,则第n次得到4n+1个正方形,
4n+1=201
4n=200
n=50
若要得到201个正方形,需要操作50次。
故答案为:21;50。
第一空:根据题干的内容,找出本题的规律,并用关系式总结出来;
第二空:把201代入关系式中进行解答。
21.1356.48;904.32
解:12÷2=6(分米)
3.14×62×12
=113.04×12
=1356.48(立方分米)
1356.48×=904.32(立方分米)。
故答案为:1356.48;904.32。
这个圆柱的体积=π×半径2×高; 其中,高=直径=正方体的棱长;削去部分的体积=这个圆柱的体积×。
22.45
解:50÷25%=200(人)
200×22.5%=45(人)
故答案为:45。
玩游戏的人数÷玩游戏的人数占总人数的百分率=总人数,总人数×查资料的人数占总人数的百分率=查资料的人数。
23.6;8
解:÷=6(天);
1÷=8(天)。
故答案为:6;8。
每天运的质量=这批货物的总质量÷平均每天运的质量;运完需要的天数=1÷平均每天运的分率。
24.-11034
解:低于海平面11034米,记作:-11034米。
故答案为:-11034。
正数和负数表示具有相反意义的量,高于海平面的记作正数,低于海平面的记作负数。
25.50;4;2;2;2;8
解:张老师带了45名学生去划船,共租了10条船,正好坐满。其中每条大船可以坐5人,每条小船可以坐3人。假设10条船全部是大船,一共能坐10×5=50人,比实际的46人多4人。把1条大船换成1条小船,就会少坐5-3=2人。多出的人数一共要换4÷2=2条小船,所以小船租了2条,大船租了10-2=8条。
故答案为:50;4;2;2;2;8。
假设全部都是大船,则共可以坐50人,比46人多4人,是因为把小船也当作坐5人来计算了,这样每条小船多算了2人,因此用一共多算的人数除以每条小船多算的人数即可求出小船的条数,进而求出大船的条数。
26.(100﹣12a);8
解:买粽子花的钱数:12a元,
应找回的钱数:(100-12a)元,
12a=100,
a=100÷12,
a=8......4
a的值最大可以是8。
故答案为:(100﹣12a);8。
第一空:每个粽子的钱数×12=买粽子花的钱数,付给售货员的钱数-买粽子花的钱数=应找回的钱数;
第二空:买粽子花的钱数小于或等于付给售货员的钱数,据此求出a的最大值。
27.-120
解:如果把陆莎从A点出发向东直线行走200米,记作+200米,那么她从A点出发先向东直线行走360米,再沿原路向西直线行走480米,最后她走的路程可记作-120米。
故答案为:-120。
正负数表示相反意义的量,向东记作正,那么向西就记作负。先向东直线行走360米,再沿原路向西直线行走480米,相当于向西走了120米,所以记作-120米。
28.1356.48;904.32
解:圆柱的底面直径是12分米,底面半径是6分米,高是12分米,
圆柱的体积:3.14×6×6×12=113.04×12=1356.48(立方分米)
圆锥的体积:1356.48×=904.32(立方分米)
故答案为:1356.48;904.32。
圆柱的体积=π×底面半径的平方×高,削去的体积=圆柱的体积×。
29.60;9.09;
解:0.6×100=60,所以0.6平方米=60平方分米,
9090÷1000=9.09,所以9090毫升=9.09升,
20分÷60=时,所以3时20分=小时。
故答案为:60;9.09;。
1平方米=100平方分米,1升=1000毫升,1时=60分;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
30.1:4;3
解:16÷4=4,所以是按照1:4的比缩小,高是12÷4=3(厘米)。
故答案为:1:4;3。
用原来的底除以现在的底求出底缩小的倍数,然后写出缩小后底与原来底的比即可求出缩小的比,然后把高也缩小相同的倍数求出现在的高。
31.5;60
解:
15和20的最大公因数是:5,最小公倍数是:
5×3×4
=15×4
=60
故答案为:5;60。
根据题意可知求两个数的最大公因数和最小公倍数,用短除法,依次除以这两数公有的质因数,直到最后两个数是互质数为止。
32.15
解:60-45=15(厘米)。
故答案为:15。
甲虫从A地出发,先向西偏南30°方向爬了45厘米到达B地,然后又原路返回爬了60厘米,则 这时甲虫离A地的距离=60-45=15厘米。
33.50;18;60;六
解:=(3×10):(5×10)=30:50;
=(3×6)÷(5×6)=18÷30;
=3÷5=0.6=60%=六折;
所以30:50==18÷30=60%=六折。
故答案为:50;18;60;六。
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就等于几成;百分之几十就是几折;比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
34.(1)
(2)
解:(1)×××××
=××××
=×××
=××
=×
=;
(2)
=(1-)+(-)+(-)+···+(-)
=1-+-+-++···-
=1-
=。
故答案为:;。
(1)观察发现①的面积是,②的面积是=······,n的面积是2的n次方分之一,据此计算;
(2)=1-=。
35.2;1600
解:8×10÷40
=80÷40
=2(毫米)
16÷4=4(厘米)
4÷÷100
=4÷÷100
=4000÷100
=40(米)
40×40=1600(平方米)。
故答案为:2;1600。
实际距离=图上距离÷比例尺;正方形的边长×正方形的边长=面积,求出正方形的边长=4厘米,然后求出实际距离,依据正方形的面积公式求出面积。
36.3000
解:1米=100厘米
60÷2×100
=30×100
=3000(立方厘米)。
故答案为:3000。
原来这根木料的体积=横截面的面积×长方体木料原来的长度;其中,横截面的面积=增加的表面积÷2。
37.(a-);a
解:a-=(a-)(米);
a-a=a(米)。
故答案为:(a-);a。
用去米,还剩下的米数=这根绳子的总米数-用去的米数; 用去,还剩下的米数=这根绳子的总米数-这根绳子的总米数×用去的分率。
38.30;圆锥;439.6
解:面积:12×5÷2=30(平方厘米);
以它的两条直角边所在的直线各旋转一周,得到两个不同的圆锥,它们的体积相差:
3.14×122×5×-3.14×52×12×
=3.14×240-3.14×100
=3.14×140
=439.6(立方厘米)
故答案为:30;圆锥;439.6。
三角形中斜边最长,因此两条较短的边就是三角形的两条直角边,根据三角形面积公式计算面积。以三角形的一条直角边为轴旋转一周会得到一个圆锥,为轴的那条直角边是圆锥的高,另一条直角边就是圆锥的底面半径,计算出两个圆锥的体积,相减后就是体积相差的部分。
39.50;18;60;六;0.6
解:3÷5=3:5==0.6=60%=六成,
3:5=30:50;=。
故答案为:50;18;60;六;0.6。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
比的基本性质:比的前项和后项同时乘或除以(0除外)相同的数,比值不变;
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;
成数表示一个数是另一个数的十分之几,统称几成。
40.30;150
解:(360÷2)÷(1+)
=180÷
=150
180-150=30。
故答案为:30;150。
差+减数=被减数=360÷2=180,减数=180÷(1+)=150,差=180-150=30。
41.20或120
解:180°÷(1+4+4)×1
=180°÷9
=20°;
180°÷(1+1+4)×4
=180°÷6×4
=30°×4
=120°。
故答案为:20或120。
①这个等腰三角形顶角的度数=三角形的内角和÷总份数×顶角占的份数×顶角占的份数;②这个等腰三角形顶角的度数=三角形的内角和÷总份数×顶角占的份数。
42.7;
解:4÷(1-)=4÷=7(米)
7-=6(米)
故答案为:7;6。
第一空:剩下的长度÷剩下的长度占全长的几分之几=这根绳子原来长;
第二空:这根绳子原来长-剪去的长度=还剩的长度。
43.25;20
解:(25-20)÷20
=5÷20
=25%
(25-20)÷25
=5÷25
=20%。
故答案为:25;20。
女生比男生多的百分率=(男生人数-女生人数)÷男生人数;男生比女生少的百分率=(男生人数-女生人数)÷女生人数。
44.11
解:假设全部租的大船,则租小船的条数:
(12×5-38)÷(5-3)
=22÷2
=11(条)。
故答案为:11。
假设全部租的大船,则租小船的条数=(平均每条大船限乘的人数×总条数-去划船的总人数)平均每条大船限乘的人数÷(平均每条大船限乘的人数-平均每条小船限乘的人数)。
45.四;5
解:(31-22+1+22)÷9
=32÷9
=3······5,则是四九的第5天。
故答案为:四;5。
从2022年12月22日~2023年1月22日经过的天数=(12月的天数-22天+1天+22天) =32天,32天里有3个9还剩下5天,所以是四九的第5天。
46.37.68
解:高:37.68÷(3.14×2×2)=37.68÷12.56=3(厘米);
体积:3.14×22×3=37.68(平方厘米)。
故答案为:37.68。
用圆柱的侧面积除以底面周长即可求出圆柱的高,然后用圆柱的底面积乘高即可求出圆柱的体积。
47.四十九亿九千八百万;50.0
解:4998000000读作:四十九亿九千八百万;
4998000000≈50.0亿。
故答案为:四十九亿九千八百万;50.0。
亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零;用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
48.正;18.9
解:在阳光下,同一时间、同一地点物体的高度和影长成正比例。如果某一刻一根竹竿高3米,影长2米,同一时刻、同一地点一幢教学楼的影长是12.6米,那么教学楼高:12.6×(3÷2)=18.9米。
故答案为:正;18.9。
同一时间、同一地点物体的高度和影长的比值是不变的,二者成正比例。竹竿高3米,影长2米,用3除以2求出竹竿是影长的几倍,然后把教学楼的影长乘这个倍数即可求出教学楼的高度。
49.40;48
解:5+6=11,80~90之间11的倍数是88,所以总人数的88人;
88÷11=8(人)
男生:8×5=40(人)
女生:8×6=48(人)
故答案为:40;48。
男生和女生的总份数是11,根据人数的特殊性,总人数一定是11的倍数,因此找出80~90之间11的倍数就是总人数。用总人数除以总份数求出每份数,然后分别求出男生和女生的人数。
50.25
解:(-)÷
=×
=25%
故答案为:25。
把这项工作看作单位“1”,用分数分别表示处两人的工作效率,用两人的工作效率差除以徒弟的工作效率即可求出师傅的工作效率比徒弟的工作效率多百分之几。
同课章节目录
