2024-2025学年小升初数学备考真题分类汇编(广东地区专版)专题1 单项选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(广东地区专版)专题1 单项选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 07:27:28 | ||
图片预览




文档简介
专题1 单项选择题-2023-2024学年
小升初数学备考真题分类汇编(广东地区专版)
试卷说明:
本试卷试题精选自广东省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广东省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·广州)甲、乙两人从400 米的环形跑道的一点A背向同时出发,8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米,那么,两人第三次相遇的地点与A点沿跑道上的最短距离是( )。
A.166米 B.176米 C.224米 D.234米
2.(2024·天河)以下各项中,两种量成反比例关系的是( )
A.生产零件的总时间一定,生产每个零件的时间和生产总数量。
B.长方形周长一定,长和宽。
C.车轮周长一定,车轮行驶的路程和转数。
D.人的年龄与身高。
3.(2024·深圳)按规律1,8,27,( ),125,括号里的数应为( )。
A.30 B.64 C.80 D.100
4.(2024·广州)钟表表示2点30分时,时针和分针所成的较小的角是( )度。
A.75 B.95 C.105 D.120
5.(2024·广州)从A城到B城,甲车要用小时,乙车要用小时,那么,甲车速度比乙车( )。
A.快25% B.慢25% C.快20% D.慢20%
6.(2024·广州)某景区“十一”假期期间接待了国内外游客5.17万人次,实现景区门票收入253万元,游客人数比去年增长一成,去年的门票收入是( )万元。(门票价格不变)
A.517 B.278.3 C.253 D.230
7.(2024·广州)一本书打七折出售是84元,比原价便宜了( )元。
A.12 B.36 C.63 D.21
8.(2024·广州)下列说法中,正确的有( )。
①正数和负数可以表示具有相反意义的量。 ②所有的数不是正数就是负数。
③正数的前面必须写正号,负数的前面必须写负号。 ④+3读作加3,-8读作减8。
A.① B.①② C.①②③ D.②③
9.(2024·广州),如果把被除数、除数同时扩大到原来的100 倍,那么它的结果是( )。
A.商5余2 B.商500余2 C.商5余200 D.商500余200
10.(2024·广州)一长方体,把它切成3个正方体,一个小正方体的表面积是24平方厘米,原长方体的表面积是( )。
A.24平方厘米 B.48平方厘米 C.56平方厘米 D.72平方厘米
11.(2024·广州)李明的自行车轮胎外直径是0.7米,他骑这辆自行车以每分钟100圈的速度通过一座2100米的大桥,需要( )(π取3)。
A.5分钟 B.7分钟 C.10分钟 D.15分钟
12.(2024·广州)设 那么( )。
A.A>B B.A=B C.A13.(2024·广州)。
A.9 B.0.09 C.0.009 D.0.0009
14.(2024·广州)元旦来临,各大商场都设计了促进消费、增加利润的促销措施。“物美”商场把一类双肩背的书包按进价提高50%进行标价,然后再打出八折的优惠价,这样商场每卖出一个书包就可盈利8元,这种书包的进价是( )。
A.42元 B.40元 C.38元
15.(2024·广州)六年级一班学生人数不超过50人,在一次数学考试中,成绩优秀的占全班人数的 成绩良好的占全班人数的 成绩在及格到良好之间的占全班人数的 那么不及格的有( )人。
A.42 B.41 C.2 D.1
16.(2024·广州)有一批零件,经检验后,100个合格,1个次品。次品率为( )。
A. B. C. D.不确定
17.(2024·广州)把一段圆柱切削成一个最大的圆锥,切削掉的部分重8千克,这段圆柱重( )。
A.24 千克 B.12千克 C.16千克
18.(2024·广州)修一条路,已经修了 km,还剩下全长的 没修,已经修的和没修的长度相比,( )。
A.已修的长 B.没修的长 C.同样长 D.无法确定
19.(2024·广州)120 比100 多百分之几? 正确的算式是( )。
A.(120-100)÷100 B.(120-100)÷120 C.120÷100-1
20.(2024·广州)平面上有六个点,每两点都连成一条直线,除了原来的6个点之外,这些直线最多还有( )个交点。
A.35 B.10 C.45 D.55
21.(2024·广州)某班一次数学测验,10道选择题,每道题给出了四个选项,其中有且仅有一个选项是正确的,有7道题所有人都做对了,有3道题所有人都只做对了其中1道题。老师作考试分析时发现这3 道题选错选项的各种情况都有,且至少有两个同学选对、选错的情况完全相同。那么,参加这次测验的学生至少有( )。
A.49人 B.41人 C.37人 D.28人
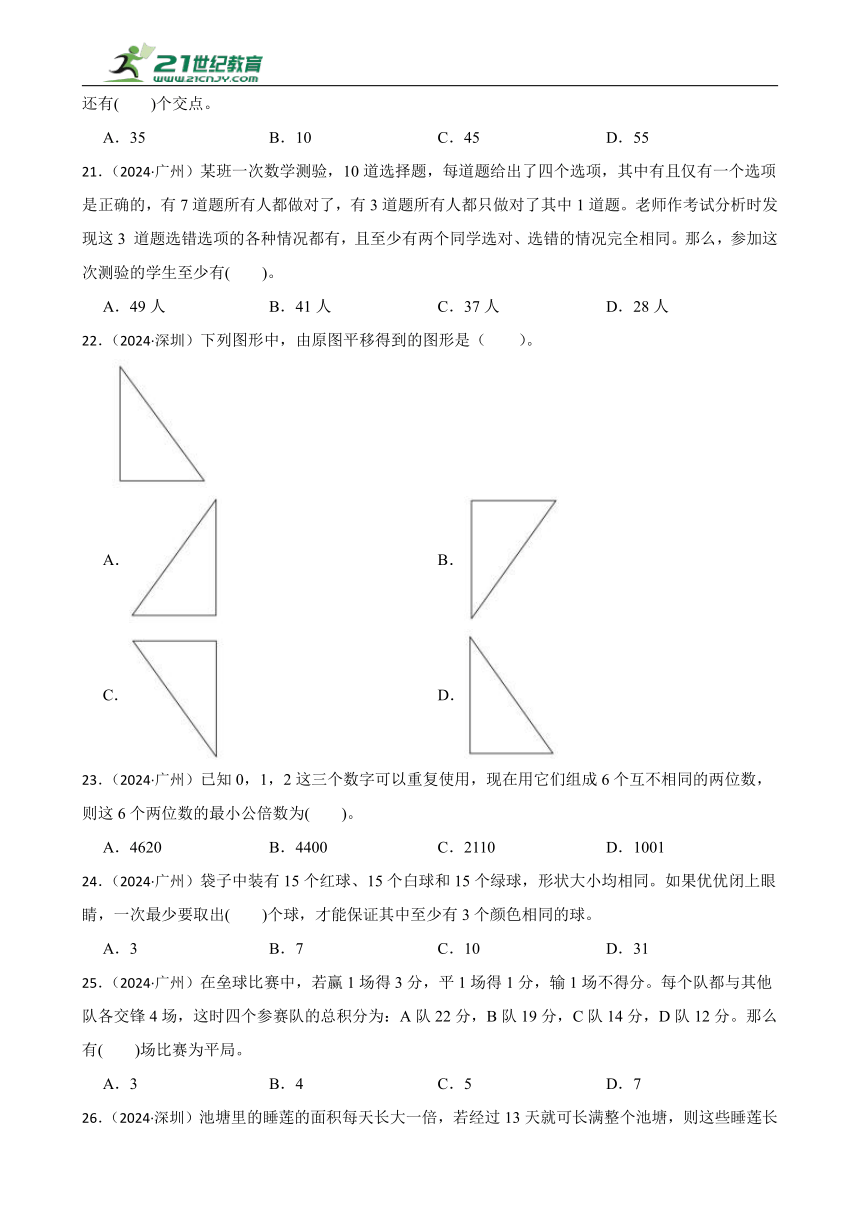
22.(2024·深圳)下列图形中,由原图平移得到的图形是( )。
A. B.
C. D.
23.(2024·广州)已知0,1,2这三个数字可以重复使用,现在用它们组成6个互不相同的两位数,则这6个两位数的最小公倍数为( )。
A.4620 B.4400 C.2110 D.1001
24.(2024·广州)袋子中装有15个红球、15个白球和15个绿球,形状大小均相同。如果优优闭上眼睛,一次最少要取出( )个球,才能保证其中至少有3个颜色相同的球。
A.3 B.7 C.10 D.31
25.(2024·广州)在垒球比赛中,若赢1场得3分,平1场得1分,输1场不得分。每个队都与其他队各交锋4场,这时四个参赛队的总积分为:A队22分,B队19分,C队14分,D队12分。那么有( )场比赛为平局。
A.3 B.4 C.5 D.7
26.(2024·深圳)池塘里的睡莲的面积每天长大一倍,若经过13天就可长满整个池塘,则这些睡莲长满半个池塘需要的天数为( )。
A.6 B.7 C.10 D.12
27.(2024·广州)一种商品的利润率为20%,进价提高25%后,保持利润不变,那么,进价提价后的利润率为( )。
A.25% B.20% C.16% D.12.5%
28.(2024·广州)小克做了9张试卷,每张试卷的满分都是100分。小克9张试卷的平均分是68分。如果不计他的最低分,那么其他8张试卷的平均分最高是( )。
A.68分 B.76.5分 C.81分 D.82.5分
29.(2024·广州)循环小数和0.432相乘,乘积也是一个循环小数,它的小数点后第2016位是( )。
A.1 B.3 C.6 D.9
30.(2024·广州)甲、乙、丙、丁四人参加某次电脑技能比赛。甲、乙两人的平均成绩为 a分,他们两人的平均成绩比丙的成绩低9分,比丁的成绩高3分,那么他们四人的平均成绩为( )分。
A.a+6 B.4a+1.5 C.a+1.5
31.(2024·云安)图( )可以围成一个圆柱。
A. B.
C. D.
32.(2024·云安)如图温度计所显示的温度是( )
A.﹣15℃ B.﹣5℃ C.5℃ D.15℃
33.(2024·云安)下列各数中,与0最接近的数是( )
A.+2 B.﹣1 C.0.5
34.(2024·深圳)在一幅比例尺是1:5000000的地图上,量得金华到杭州的距离为4厘米,则金华到杭州的实际距离是( )。
A.2000米 B.200千米 C.2000千米 D.20000米
35.(2024·深圳)李菲家客厅长4.8米,宽4.2米,选用边长( )分米的方砖铺地不需要切割。
A.4 B.6 C.8 D.12
36.(2024·深圳)把一段圆柱体圆木削成一个最大的圆锥体,圆锥体的体积是9.3立方厘米,削去部分的体积是多少?列式是( )。
A. B.
C. D.
37.(2024·深圳)圆锥的底面半径4分米,高3分米,它的体积是( )。(π取3.14)
A.150.72 立方分米 B.37.68立方分米
C.50.24立方分米 D.100.48 立方分米
38.(2024·深圳)画一个周长是12.56cm的圆,圆规两脚之间的距离是( )cm。(π取3.14)
A.2 B.3 C.4
39.(2024·广州)“世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组,在小组赛中,这4支队中的每支队都要与另3支队比赛一场。根据规定:每场比赛获胜的队得3分;失败的队得0分;如果双方踢平,两队各得1分。已知:
⑴这4支队三场比赛的总得分为4个连续奇数;
⑵乙队总得分排在第一;
⑶丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
根据以上条件可以推断,总得分排在第四的是( )队。
A.甲 B.乙 C.丙 D.丁
40.(2024·广州)由2,0,1,3四个数字组成(可重复使用)的比2013小的四位数有( )个。
A.71 B.64 C.128 D.6
41.(2024·广州)有一串真分数 按规律,第100个分数是( )。
A. B. C. D.
42.(2024·广州)甲、乙两只蜗牛在比赛爬行(如图所示),甲爬行外面的路线用了6分钟,乙爬行里面的路线用了4 分钟。甲蜗牛的速度是乙蜗牛的( )。
A. B. C. D.无法确定
43.(2024·广州)小圆的直径是大圆的半径,大圆周长与小圆周长的比是( )。
A.1:1 B.1:2 C.3:2 D.2:1
44.(2024·广州) (带余除法)在÷=a……b,如果除数是5,那么b有( )种可能性。
A.3 B.4 C.5
45.(2024·广州)(负数)如果用+3米表示高出警戒水位3米,那么低于警戒水位5米记作( )。
A.+5米 B.- 5米 C.0米 D.- 10米
46.(2024·广州)小明从13:30开始看一部电影,到15:10结束,这部电影一共放映了( )。
A.80分钟 B.100分钟
C.2 小时40分钟 D.90分钟
47.(2024·广州)下列说法正确的是( )。
A.两个图形相对于某条直线对称,则这两图形的形状必须一样,大小可以不相等
B.平移和轴对称只改变图形的形状,不能改变图形的大小
C.通过平移和轴对称得到的图形没有改变原图形的形状和大小
D.长方形不一定都是轴对称图形
48.(2024·广州)如图每个小正方形的面积均为1个面积单位,共9个面积单位,则图中阴影部分面积占正方形面积的( )。
A. B. C. D.
49.(2024·广州)有9张同样大小的圆形纸片,其中标有数字1的1张,标有数字2的2张,标有数字3的3张,标有数字4的3张。把这9张圆形纸片如图所示放置在一起,但标有相同数字的纸片不许靠在一起,如果M位置上放置标有数字2的纸片,一共有( )种不同的放法。
A.6 B.8 C.10 D.12
50.(2024·深圳)王刚同学是2003年入学的,他在四班,学号是15,如果用6位数字给他编学籍号,下面比较实用的是( )。
A.200304 B.040315 C.030415 D.150403
答案解析部分
1.B
解:根据题意,可得
8分钟=480秒
(400×3-0.1×480)÷2
=(1200-48)÷2
=1152÷2
=576(米)
576-400=176(米)
400-176=224(米)
176<224 因此最短距离是176米。
故答案为:B
两人每相遇一次就合走一圈,则第三次相遇二人共走400×3=1200(米),再算出乙8分钟所行的路程,据此根据跑道周长求解即可。
2.A
解:A项:生产总量×平均生产每个零件用的时间=生产总时间(一定),生产零件的总时间一定,生产每个零件的时间和生产总数量成反比例;
B项:长方形周长一定,长和宽不成比例;
C项:车轮行驶的路程÷转数=出轮的周长(一定),车轮周长一定,车轮行驶的路程和转数成正比例;
D项:人的年龄与身高不成比例。
故答案为:A。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
3.B
解:1=1×1×1;
8=2×2×2;
27=3×3×3;
64=4×4×4;
125=5×5×5。
故答案为:B
发现规律,第n个( )里的数字是n3。
4.C
解:根据题意,可得
时针:2×30°+30×0.5°=75°,
分针:30×6°=180°,
夹角:180°-75°=105°。
故答案为:C
钟面的一周分为60格,当分针走60格时,时针正好走5格,所以时针的速度是分针速
度的5÷60=;钟面上每2个数字之间相隔30度;时针1分钟走0.5度
5.A
%
=1÷4×100%
=25%
故答案为:A.
先求出甲、乙从A城到B城的时间之比,由路程一定速度和时间成反比求出甲、乙的速度之比,再计算甲速比乙速快的百分率.
6.D
解:根据题意,可得
5.17÷(1+10%)
=5.17÷1.1
=4.7(万人次)
(万元)
故答案为:D
游客人数比去年增长一成,则今年人数是去年人数的(1+10%),今年人数÷对应百分率=去年人数,门票价格不变,所以人数比就是收入比,根据比的应用,按比分配求出去年门票收入即可。
7.B
解:原价:84÷70% =120(元)
便宜了:120-84=36(元)
故答案为:B
原价=售价÷折扣率,再用原价减去售价求得便宜的价钱。
8.A
解:①正数和负数可以表示具有相反意义的量,说法正确。
②0既不是正数也不是负数,所以本选项说法错误。
③正数的前面可以不写正号,负数的前面必须写负号,所以本选项说法错误。
④+3读作正3,-8读作负8,所以本选项说法错误。
故答案为:A
①生活中,通常用正负数表示具有相反意义的两种量,如果规定一个量为正,那么与它相反的量就为负。
②所有的数不是正数就是负数,这种说法错误,因为0既不是正数也不是负数。
③正数的前面可以不写正号,负数的前面必须写负号。
④根据正负数的读法可知:+3读作正3,-8读作负8。
9.C
(32×100)÷(6×100)
=3200÷600
=5……200
故答案为:C.
商不变性质是被除数和除数同时乘或除以相同的数(0除外),商不变。在有余数的除法中,当被除数和除数按此规律变化时,商不变,余数要随被除数和除数的变化而变化,乘或除以相同的倍数。
10.C
24×3-24÷6×4
=72-16
故答案为:C.
先算出切开后三个小正方体的表面积之和,切成3个小正方体的过程中切两刀,表面增加了4个小正方形,再用三个小正方体表面积之和减去这4个面的面积即可.
11.C
2100÷(3×0.7×100)
(分钟)
故答案为:C.
根据圆周长公式C=πd,计算出一圈的长度,再乘100算出每分钟所行的长度,用桥长除以自行车速度可算出过桥时间.
12.A
解:A=9876543×3456789
=9876543×(3456788+1)
=9876543×3456788+9876543
B=9876544×3456788
=(9876543+1)×3456788
=9876543×3456788+3456788
因为9876543>3456788,所以A>B。
故答案为:A
通过观察,A与B两个式子中的数字存在以下关系:9876543比9876544少1,3456789比3456788多1,所以可以将A变形成9876543×(3456788+1)=9876543×3456788+9876543,B变形成9876544×3456788=(9876543+1)×3456788=9876543×3456788+3456788,然后比较大小即可。
13.C
解:根据题意,可得
0.381﹣0.31×1.2
=0.381﹣0.372
=0.009;
故答案为:C
根据在有余数的除法中,“被除数=商×除数+余数”可得:余数=被除数﹣商×除数;据此判断即可.
14.B
解:根据题意,可得
8÷[1×(1+50%)×80%-1]
=8÷[1×1.5×0.8-1]
=8÷0.2
=40(元)
答:这种书包的进价是40元
故答案为:B
把进价看作“1”,用利润除以对应分率,即可求解
15.D
解:根据题意,可得
2,3,7三个数的最小公倍数是2×3×7=42
不及格的人数为:
=1(人)
故答案为:D
六年级一班学生人数能同时被2,3,7整除,即为2,3,7的公倍数,又因为学生人数不超过50人,因此学生人数为2,3,7的最小公倍数。
16.C
解:次品率:
故答案为:C
根据:次品率=次品的个数÷总个数,解答即可。
17.B
解:根据题意,可得
故答案为:B
圆柱内削出的最大的圆锥,与原圆柱等底等高,所以圆锥的体积是圆柱的体积的,则削去部分的体积就是圆柱的体积的 ,削去的部分是8千克,根据分数除法的意义即可求出圆柱的体积.
18.A
解:已修占全长的:
故答案为:A
有量有率,从率入手,修了km后,还剩全长的,则已修的km 占全长的,,所以已修的长。
19.A
解:根据题意,可得
(120-100)÷100
=20÷100
=20%
故答案为:A
要求120比100多百分之几,就是求120比100多的部分占100的百分之几,因此用多出的部分除以100即可。
20.C
解:一共有 (条)直线,这些直线最多共有15×14÷2=105(个)交点,其中原来的6个点中每个点都在5条直线上,这6个点一共充当了 )(个)交点,于是还有105-60=45(个)。
故答案为:C
有n个点,每三个点都不在一条直线上,过其中每两个点画直线,可以画 条直线,每两条直线不重合的话,有且只有1个交点,一共可以形成的交点总数为个交点。 原始的6个点本身,每个点都是5条直线的交点,而每3条直线中至少有2条直线相交于该点,因此,每个点实际上充当了= 5 × 4 ÷2 = 10 个交点,6个点共充当 6 × 10 = 60 个交点。 最后用总的交点数中减去原有点所充当的交点数,就得到实际额外产生最多的交点数
21.D
解:根据题意,可得
3道题的错误选项的各种情况有:
(3×3)×3=27种
27+1=28(人)
故答案为:D
每道题有3个错误选项,所以3道题的错误选项的各种情况有:(3×3)×3=27种。因为至少有两个同学选对、选错的情况完全相同,所以学生人数至少为:27+1=28人。
22.D
解: 通过平移可以得到
故答案为:D
平移不改变图形的大小和形状。
23.A
解:根据题意,可得
由0、1、2这三个数字可以组成的两位数有:10、11、12、20、21、22
10=2×5,
11=11,
12=22×3,
20=22×5,
21=3×7,
22=2×11
因此,最小公倍数为:22×3×5×7×11=4620
故答案为:A
由0、1、2这三个数字可以组成的两位数有:10、11、12、20、21、22。将每个数分解为质因数:10=2×5,11=11,12=22×3,20=22×5,21=3×7,22=2×11,找出所有质因数的最高次幂,确定最小公倍数:2的最高次幂为22,3的最高次幂为3,5的最高次幂为5,7的最高次幂为7,11的最高次幂为11,因此,最小公倍数为:22×3×5×7×11=4620。
24.B
解:最坏情况:
先取2红、2白、2绿,无3个同色,
再取第7个球时,必有3个同色,
因此,最少取出7个球,才能保证3个同色,
故答案为:B
利用最不利原则,最多可取出2个红球、2个白球和2个绿球使得取出的球中不会产生3个颜色相同的球,此时再任意取出一个球,则会出现3个颜色相同的球,因此结果为2×3+1=7(个)。
25.C
解:设平x场,得:
3×(24-x)+2x=22+19+14+12
72-3x+2x=67
x=5
答:有5场比赛为平局.
故答案为:C.
每个队都与其他队交锋4场,总共进行4×3+4×2+4=24场比赛,因为输一场不得分,因此不用去管输的场数.因为平一场双双都得1分,因此平1场共得2分,设平x场,由此列方程为:3×(24-x)+2x=22+19+14+12,解方程即可.
26.D
解:因为池塘里的睡莲的面积每天长大一倍,
所以长满整个池塘的前一天这些睡莲长满半个池塘,13-1=12(天)。
故答案为:D
此题用逆推的方法解答,睡莲的面积每天长大一倍,13天睡莲面积=12 天睡莲面积×2,13 天长满整个池塘,所以12天长满半个池塘。
27.C
解:假设这种商品的成本价是100元;
利润:100×20%=20(元)
现在的成本:100×(1+25%)
=100×1.25
=125(元)
20÷125=16%
即,进价提高后的利润率为16%。
故答案为:C
假设这种商品的成本价是100元,则利润是100×20%=20(元);现在的成本是100×(1+25%)=125(元);要保持利润不变,那么用利润除以现在的成本就是进价提高后的利润率。
28.B
解:根据题意,可得
68×9÷8=76.5(分)
答:平均分最高为76.5分。
故答案为:B
小克的试卷最高100,最低0分。去除最低分让平均分最高需要让最低分等于0,这样用总分除以8就是其他8张试卷的最高平均分。总分为68×9=612(分),其他8张最高平均分为612÷8=76.5
29.B
解:根据题意,可得
=
=
=
循环小数为:,循环节为“63”。
第2016位数字为:2016 2=2014
2014÷2=1007,余数为0。
因此,第2016位数字是循环节中的最后一位,即3。
故答案为:B
先将循环小数 化成分数:,然后再根据题意,,然后化简,再化成循环小数:,确定循环节“63”,确定第2016位的数字2014,在循环节中,2014除以循环节的长度(即2),得到1007余0,据此即可判断循环节中最后一位数
30.C
解:由题意知,丙的成绩是(a+9)分,丁的成绩是(a-3)分,
则他们四人的平均成绩为:
[ 2a+( a+9)+( a-3) ]÷4
=( 4a+6)÷4
=a+1.5,
故答案为:C
先表示出丙的成绩是(a+9)分,丁的成绩是(a-3)分,然后把甲、乙、丙、丁的成绩相加,再除以4,计算即可得解。
31.A
解:3.14÷3.14=1,2÷2=1,A能围成圆柱。
故答案为:A。
要围成圆柱的底面直径=2÷2=1,圆柱的直径=底面周长÷π,两者相等是就能围成圆柱。
32.B
解:温度计所显示的温度是在0度以下是-5℃。
故答案为:B。
正数和负数表示具有相反意义的量;零上温度记作正数,零下温度记作负数, 温度计所显示的温度是在0度以下是-5℃。
33.C
解:A项:2-0=2;
B项:0-(-1)=1;
C项:0.5-0=0.5;
2>1>0.5,0.5与0最接近。
故答案为:C。
分别计算出0与各项数的差,差最小的最接近0。
34.B
解:(厘米),
20000000 厘米=200千米。
故答案为:B
1千米=100000厘米,计算金华到杭州的实际距离,需要利用地图比例尺的知识,根据图上距离与比例尺的关系来求解。
35.B
解:4.2米=42分米,
4.8米=48分米
42=2×3×7,
48=2×2×2×2×3,
所以42和48的最大公因数为:2×3=6。
故答案为:B
要找到不需要切割的方砖边长,需先将客厅的长和宽单位换算成分米,然后找出长和宽的公因数,判断每个选项是否为公因数。
36.B
解:
=9.3×3-9.3
=27.9-9.3
=18.6(立方厘米)
故答案为:B
首先要明确等底等高的圆锥与圆柱体积之间的关系,通过已知圆锥体积求出圆柱体积,再依据两者关系求出削去部分体积,最后根据运算逻辑判断选项。
37.C
解:
=50.24(立方分米)
故答案为:C
根据圆锥体积公式 V= π r2, (π取3.14) ,我们需要将题目中给出的半径和高的值代入公式计算体积,然后与选项进行对比得出答案。
38.A
解:12.56÷(2×3.14)
=12.56÷6.28
=2(cm)
故答案为:A
圆规两脚间的距离就是所画圆的半径。要求这个距离,就需要根据已知的圆周长,利用圆的周长公式来计算半径。
39.C
解:四队的得分为9,7,5,3或者7,5,3,1,据题意可知,乙队的分数只能是7分。
丁队得分为5分,甲队得分为3分,丙队得分为1分。
故答案为:C
一场胜利可以得到3分,则3场比赛最多得到9分,由题知这4支队伍得分为4个连续奇数,且丁队有2场踢平。因此乙队排名第一,得分为7分(如果剩下那场是负的话,丁得分就为偶数);据比赛规则及得分为连续的奇数可知,乙为两胜一平,丁为两平一胜,丙为一平两负,甲为两负一胜,所以丙得分最少。
40.A
解:根据题意,可得
以1为首位的共有: (个)
以2为首位的共有: (个)
共有64+7=71(个)
故答案为:A
以1为首位时,百位、十位、个位三个数位上都可以在2,0,1,3四个数字中任选,共有(4×4×4)种可能。
以2为首位时,百位上只能是0,当十位上是1时个位只能小于3,可选2,0,1,有3种可能。
当十位上是0时,个位就可在2,0,1,3四个数中任选一个,有4种可能。
41.A
解:根据题意,可得
(个)
100-91=9(个)
第100个分数是
故答案为:A
观察这串分数的分母变化规律,分母是n,就有(n-1)个以此为分母的分数,然后计算出分数分母是2~14的分数的个数,即可推出第100 个分数是分母为15 的第9个分数,即
42.B
解:如图
甲:π×(r1+r2)÷2
=
乙:π×r1÷2+π×r2÷2
=
=
因为=,所以甲蜗牛爬行的路线和乙蜗牛爬行的路线长度相等。
假设两条路线的长度均为1。
(1÷6)÷(1÷4)
=
=
=
所以,甲蜗牛的速度是乙蜗牛的。
故答案为:B
根据“C=πd”求出甲爬行路线和乙爬行路线的长度,计算可知,两条路线的长度相等,假设出两条路线的长度,根据“速度=路程÷时间”表示出两只蜗牛的速度,最后用除法求出甲蜗牛的速度占乙蜗牛速度的分率,据此解答。
43.D
解:根据题意,可得
直径:小圆:大圆=1:2,
周长:小圆:大圆=1:2。
故答案为:D
圆的周长=2×圆的半径×π=圆的直径×π,由此可以的得出,两个圆的周长比=两个圆的直径比=两个圆的半径比
44.B
解:在除法运算中,余数总是小于除数。
因为除数是5,所以b可以是1,2,3,4,共有4种可能性。
故答案为:B
在带余除法中,余数必须小于除数,因为除数是5,据此余数必须小于5,据此即可求解
45.B
解:根据题意,可得
如果用+3米表示高出警戒水位3米,那么低于警戒水位5米记作-5
故答案为:B
题目明确指出,高出警戒水位3米用+3米表示。基于此规则,对于低于警戒水位的情况,应该使用负数来表示。根据题目描述,低于警戒水位5米应记作-5米,据此即可求解
46.B
解:15时10分-13时10分=1 小时40分
1 小时40分=100分钟。
故答案为:B
从电影放映时间等于结束时间减去开始时间,然后将结果转换成分钟。 从13:30到14:30,我们经过了一个完整的小时。然后,从14:30到15:10,我们又经过了40分钟。因此,总时间是1小时40分钟, 据此可解。
47.C
解:选项A:根据轴对称的定义,两个图形如果关于某条直线对称,它们的形状和大小必须完全相等,因此A项不正确。
选项B:平移和轴对称都不改变图形的形状和大小,只改变图形的位置,因此B项的描述是错误的。
选项C:准确反映了平移和轴对称的性质,因此C项正确。
选项D:所有长方形都是轴对称图形,因为它们都至少有两条对称轴:一条是通过较长边的中点,另一条是通过较短边的中点。因此D项不正确。
故答案为:C。
(1)轴对称和平移的性质:轴对称是指图形沿某条直线折叠后能完全重合,而平移是指将图形沿着直线方向移动一定距离。两者都不改变图形的大小和形状,只改变图形的位置。
(2)轴对称图形的概念,即存在一条或多条直线,使得图形相对于这条直线折叠时,图形的两部分完全重合。
48.B
解:根据题意,可得,
则 =4,
那么阴影部分面积占正方形面积的
故答案为:
图中阴影部分的面积=大正方形面积-周边3个三角形的面积,阴影部分面积÷正方形面积即可。
49.D
解:首先考虑特殊数字2的位置,当2在左下角时,1如果放置在右下角,4和3 有两种位置。
如果1不放置在右下角的位置,只能放置在紧挨着右下角的两个位置,每种情况都有2种,所以有4种位置。
根据对称性,2在右下角的情况与前相同,则共有:(4+2)×2=12(种)。
答:一共有12种不同的放法.
故答案为:D.
首先考虑特殊的数字2的位置,(1)当2在左下角时,1如果放置在右下角;(2)如果1不放置在右下角的位置;分两类讨论即可,然后2在右下角与前相同.
50.C
解:根据“年份+班号+学号”编号为030415。
故答案为:C
对王刚同学的学籍号进行编排,按照从大范围到小范围的顺序,依次是入学年份、班级、学号。
小升初数学备考真题分类汇编(广东地区专版)
试卷说明:
本试卷试题精选自广东省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广东省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·广州)甲、乙两人从400 米的环形跑道的一点A背向同时出发,8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米,那么,两人第三次相遇的地点与A点沿跑道上的最短距离是( )。
A.166米 B.176米 C.224米 D.234米
2.(2024·天河)以下各项中,两种量成反比例关系的是( )
A.生产零件的总时间一定,生产每个零件的时间和生产总数量。
B.长方形周长一定,长和宽。
C.车轮周长一定,车轮行驶的路程和转数。
D.人的年龄与身高。
3.(2024·深圳)按规律1,8,27,( ),125,括号里的数应为( )。
A.30 B.64 C.80 D.100
4.(2024·广州)钟表表示2点30分时,时针和分针所成的较小的角是( )度。
A.75 B.95 C.105 D.120
5.(2024·广州)从A城到B城,甲车要用小时,乙车要用小时,那么,甲车速度比乙车( )。
A.快25% B.慢25% C.快20% D.慢20%
6.(2024·广州)某景区“十一”假期期间接待了国内外游客5.17万人次,实现景区门票收入253万元,游客人数比去年增长一成,去年的门票收入是( )万元。(门票价格不变)
A.517 B.278.3 C.253 D.230
7.(2024·广州)一本书打七折出售是84元,比原价便宜了( )元。
A.12 B.36 C.63 D.21
8.(2024·广州)下列说法中,正确的有( )。
①正数和负数可以表示具有相反意义的量。 ②所有的数不是正数就是负数。
③正数的前面必须写正号,负数的前面必须写负号。 ④+3读作加3,-8读作减8。
A.① B.①② C.①②③ D.②③
9.(2024·广州),如果把被除数、除数同时扩大到原来的100 倍,那么它的结果是( )。
A.商5余2 B.商500余2 C.商5余200 D.商500余200
10.(2024·广州)一长方体,把它切成3个正方体,一个小正方体的表面积是24平方厘米,原长方体的表面积是( )。
A.24平方厘米 B.48平方厘米 C.56平方厘米 D.72平方厘米
11.(2024·广州)李明的自行车轮胎外直径是0.7米,他骑这辆自行车以每分钟100圈的速度通过一座2100米的大桥,需要( )(π取3)。
A.5分钟 B.7分钟 C.10分钟 D.15分钟
12.(2024·广州)设 那么( )。
A.A>B B.A=B C.A13.(2024·广州)。
A.9 B.0.09 C.0.009 D.0.0009
14.(2024·广州)元旦来临,各大商场都设计了促进消费、增加利润的促销措施。“物美”商场把一类双肩背的书包按进价提高50%进行标价,然后再打出八折的优惠价,这样商场每卖出一个书包就可盈利8元,这种书包的进价是( )。
A.42元 B.40元 C.38元
15.(2024·广州)六年级一班学生人数不超过50人,在一次数学考试中,成绩优秀的占全班人数的 成绩良好的占全班人数的 成绩在及格到良好之间的占全班人数的 那么不及格的有( )人。
A.42 B.41 C.2 D.1
16.(2024·广州)有一批零件,经检验后,100个合格,1个次品。次品率为( )。
A. B. C. D.不确定
17.(2024·广州)把一段圆柱切削成一个最大的圆锥,切削掉的部分重8千克,这段圆柱重( )。
A.24 千克 B.12千克 C.16千克
18.(2024·广州)修一条路,已经修了 km,还剩下全长的 没修,已经修的和没修的长度相比,( )。
A.已修的长 B.没修的长 C.同样长 D.无法确定
19.(2024·广州)120 比100 多百分之几? 正确的算式是( )。
A.(120-100)÷100 B.(120-100)÷120 C.120÷100-1
20.(2024·广州)平面上有六个点,每两点都连成一条直线,除了原来的6个点之外,这些直线最多还有( )个交点。
A.35 B.10 C.45 D.55
21.(2024·广州)某班一次数学测验,10道选择题,每道题给出了四个选项,其中有且仅有一个选项是正确的,有7道题所有人都做对了,有3道题所有人都只做对了其中1道题。老师作考试分析时发现这3 道题选错选项的各种情况都有,且至少有两个同学选对、选错的情况完全相同。那么,参加这次测验的学生至少有( )。
A.49人 B.41人 C.37人 D.28人
22.(2024·深圳)下列图形中,由原图平移得到的图形是( )。
A. B.
C. D.
23.(2024·广州)已知0,1,2这三个数字可以重复使用,现在用它们组成6个互不相同的两位数,则这6个两位数的最小公倍数为( )。
A.4620 B.4400 C.2110 D.1001
24.(2024·广州)袋子中装有15个红球、15个白球和15个绿球,形状大小均相同。如果优优闭上眼睛,一次最少要取出( )个球,才能保证其中至少有3个颜色相同的球。
A.3 B.7 C.10 D.31
25.(2024·广州)在垒球比赛中,若赢1场得3分,平1场得1分,输1场不得分。每个队都与其他队各交锋4场,这时四个参赛队的总积分为:A队22分,B队19分,C队14分,D队12分。那么有( )场比赛为平局。
A.3 B.4 C.5 D.7
26.(2024·深圳)池塘里的睡莲的面积每天长大一倍,若经过13天就可长满整个池塘,则这些睡莲长满半个池塘需要的天数为( )。
A.6 B.7 C.10 D.12
27.(2024·广州)一种商品的利润率为20%,进价提高25%后,保持利润不变,那么,进价提价后的利润率为( )。
A.25% B.20% C.16% D.12.5%
28.(2024·广州)小克做了9张试卷,每张试卷的满分都是100分。小克9张试卷的平均分是68分。如果不计他的最低分,那么其他8张试卷的平均分最高是( )。
A.68分 B.76.5分 C.81分 D.82.5分
29.(2024·广州)循环小数和0.432相乘,乘积也是一个循环小数,它的小数点后第2016位是( )。
A.1 B.3 C.6 D.9
30.(2024·广州)甲、乙、丙、丁四人参加某次电脑技能比赛。甲、乙两人的平均成绩为 a分,他们两人的平均成绩比丙的成绩低9分,比丁的成绩高3分,那么他们四人的平均成绩为( )分。
A.a+6 B.4a+1.5 C.a+1.5
31.(2024·云安)图( )可以围成一个圆柱。
A. B.
C. D.
32.(2024·云安)如图温度计所显示的温度是( )
A.﹣15℃ B.﹣5℃ C.5℃ D.15℃
33.(2024·云安)下列各数中,与0最接近的数是( )
A.+2 B.﹣1 C.0.5
34.(2024·深圳)在一幅比例尺是1:5000000的地图上,量得金华到杭州的距离为4厘米,则金华到杭州的实际距离是( )。
A.2000米 B.200千米 C.2000千米 D.20000米
35.(2024·深圳)李菲家客厅长4.8米,宽4.2米,选用边长( )分米的方砖铺地不需要切割。
A.4 B.6 C.8 D.12
36.(2024·深圳)把一段圆柱体圆木削成一个最大的圆锥体,圆锥体的体积是9.3立方厘米,削去部分的体积是多少?列式是( )。
A. B.
C. D.
37.(2024·深圳)圆锥的底面半径4分米,高3分米,它的体积是( )。(π取3.14)
A.150.72 立方分米 B.37.68立方分米
C.50.24立方分米 D.100.48 立方分米
38.(2024·深圳)画一个周长是12.56cm的圆,圆规两脚之间的距离是( )cm。(π取3.14)
A.2 B.3 C.4
39.(2024·广州)“世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组,在小组赛中,这4支队中的每支队都要与另3支队比赛一场。根据规定:每场比赛获胜的队得3分;失败的队得0分;如果双方踢平,两队各得1分。已知:
⑴这4支队三场比赛的总得分为4个连续奇数;
⑵乙队总得分排在第一;
⑶丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
根据以上条件可以推断,总得分排在第四的是( )队。
A.甲 B.乙 C.丙 D.丁
40.(2024·广州)由2,0,1,3四个数字组成(可重复使用)的比2013小的四位数有( )个。
A.71 B.64 C.128 D.6
41.(2024·广州)有一串真分数 按规律,第100个分数是( )。
A. B. C. D.
42.(2024·广州)甲、乙两只蜗牛在比赛爬行(如图所示),甲爬行外面的路线用了6分钟,乙爬行里面的路线用了4 分钟。甲蜗牛的速度是乙蜗牛的( )。
A. B. C. D.无法确定
43.(2024·广州)小圆的直径是大圆的半径,大圆周长与小圆周长的比是( )。
A.1:1 B.1:2 C.3:2 D.2:1
44.(2024·广州) (带余除法)在÷=a……b,如果除数是5,那么b有( )种可能性。
A.3 B.4 C.5
45.(2024·广州)(负数)如果用+3米表示高出警戒水位3米,那么低于警戒水位5米记作( )。
A.+5米 B.- 5米 C.0米 D.- 10米
46.(2024·广州)小明从13:30开始看一部电影,到15:10结束,这部电影一共放映了( )。
A.80分钟 B.100分钟
C.2 小时40分钟 D.90分钟
47.(2024·广州)下列说法正确的是( )。
A.两个图形相对于某条直线对称,则这两图形的形状必须一样,大小可以不相等
B.平移和轴对称只改变图形的形状,不能改变图形的大小
C.通过平移和轴对称得到的图形没有改变原图形的形状和大小
D.长方形不一定都是轴对称图形
48.(2024·广州)如图每个小正方形的面积均为1个面积单位,共9个面积单位,则图中阴影部分面积占正方形面积的( )。
A. B. C. D.
49.(2024·广州)有9张同样大小的圆形纸片,其中标有数字1的1张,标有数字2的2张,标有数字3的3张,标有数字4的3张。把这9张圆形纸片如图所示放置在一起,但标有相同数字的纸片不许靠在一起,如果M位置上放置标有数字2的纸片,一共有( )种不同的放法。
A.6 B.8 C.10 D.12
50.(2024·深圳)王刚同学是2003年入学的,他在四班,学号是15,如果用6位数字给他编学籍号,下面比较实用的是( )。
A.200304 B.040315 C.030415 D.150403
答案解析部分
1.B
解:根据题意,可得
8分钟=480秒
(400×3-0.1×480)÷2
=(1200-48)÷2
=1152÷2
=576(米)
576-400=176(米)
400-176=224(米)
176<224 因此最短距离是176米。
故答案为:B
两人每相遇一次就合走一圈,则第三次相遇二人共走400×3=1200(米),再算出乙8分钟所行的路程,据此根据跑道周长求解即可。
2.A
解:A项:生产总量×平均生产每个零件用的时间=生产总时间(一定),生产零件的总时间一定,生产每个零件的时间和生产总数量成反比例;
B项:长方形周长一定,长和宽不成比例;
C项:车轮行驶的路程÷转数=出轮的周长(一定),车轮周长一定,车轮行驶的路程和转数成正比例;
D项:人的年龄与身高不成比例。
故答案为:A。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
3.B
解:1=1×1×1;
8=2×2×2;
27=3×3×3;
64=4×4×4;
125=5×5×5。
故答案为:B
发现规律,第n个( )里的数字是n3。
4.C
解:根据题意,可得
时针:2×30°+30×0.5°=75°,
分针:30×6°=180°,
夹角:180°-75°=105°。
故答案为:C
钟面的一周分为60格,当分针走60格时,时针正好走5格,所以时针的速度是分针速
度的5÷60=;钟面上每2个数字之间相隔30度;时针1分钟走0.5度
5.A
%
=1÷4×100%
=25%
故答案为:A.
先求出甲、乙从A城到B城的时间之比,由路程一定速度和时间成反比求出甲、乙的速度之比,再计算甲速比乙速快的百分率.
6.D
解:根据题意,可得
5.17÷(1+10%)
=5.17÷1.1
=4.7(万人次)
(万元)
故答案为:D
游客人数比去年增长一成,则今年人数是去年人数的(1+10%),今年人数÷对应百分率=去年人数,门票价格不变,所以人数比就是收入比,根据比的应用,按比分配求出去年门票收入即可。
7.B
解:原价:84÷70% =120(元)
便宜了:120-84=36(元)
故答案为:B
原价=售价÷折扣率,再用原价减去售价求得便宜的价钱。
8.A
解:①正数和负数可以表示具有相反意义的量,说法正确。
②0既不是正数也不是负数,所以本选项说法错误。
③正数的前面可以不写正号,负数的前面必须写负号,所以本选项说法错误。
④+3读作正3,-8读作负8,所以本选项说法错误。
故答案为:A
①生活中,通常用正负数表示具有相反意义的两种量,如果规定一个量为正,那么与它相反的量就为负。
②所有的数不是正数就是负数,这种说法错误,因为0既不是正数也不是负数。
③正数的前面可以不写正号,负数的前面必须写负号。
④根据正负数的读法可知:+3读作正3,-8读作负8。
9.C
(32×100)÷(6×100)
=3200÷600
=5……200
故答案为:C.
商不变性质是被除数和除数同时乘或除以相同的数(0除外),商不变。在有余数的除法中,当被除数和除数按此规律变化时,商不变,余数要随被除数和除数的变化而变化,乘或除以相同的倍数。
10.C
24×3-24÷6×4
=72-16
故答案为:C.
先算出切开后三个小正方体的表面积之和,切成3个小正方体的过程中切两刀,表面增加了4个小正方形,再用三个小正方体表面积之和减去这4个面的面积即可.
11.C
2100÷(3×0.7×100)
(分钟)
故答案为:C.
根据圆周长公式C=πd,计算出一圈的长度,再乘100算出每分钟所行的长度,用桥长除以自行车速度可算出过桥时间.
12.A
解:A=9876543×3456789
=9876543×(3456788+1)
=9876543×3456788+9876543
B=9876544×3456788
=(9876543+1)×3456788
=9876543×3456788+3456788
因为9876543>3456788,所以A>B。
故答案为:A
通过观察,A与B两个式子中的数字存在以下关系:9876543比9876544少1,3456789比3456788多1,所以可以将A变形成9876543×(3456788+1)=9876543×3456788+9876543,B变形成9876544×3456788=(9876543+1)×3456788=9876543×3456788+3456788,然后比较大小即可。
13.C
解:根据题意,可得
0.381﹣0.31×1.2
=0.381﹣0.372
=0.009;
故答案为:C
根据在有余数的除法中,“被除数=商×除数+余数”可得:余数=被除数﹣商×除数;据此判断即可.
14.B
解:根据题意,可得
8÷[1×(1+50%)×80%-1]
=8÷[1×1.5×0.8-1]
=8÷0.2
=40(元)
答:这种书包的进价是40元
故答案为:B
把进价看作“1”,用利润除以对应分率,即可求解
15.D
解:根据题意,可得
2,3,7三个数的最小公倍数是2×3×7=42
不及格的人数为:
=1(人)
故答案为:D
六年级一班学生人数能同时被2,3,7整除,即为2,3,7的公倍数,又因为学生人数不超过50人,因此学生人数为2,3,7的最小公倍数。
16.C
解:次品率:
故答案为:C
根据:次品率=次品的个数÷总个数,解答即可。
17.B
解:根据题意,可得
故答案为:B
圆柱内削出的最大的圆锥,与原圆柱等底等高,所以圆锥的体积是圆柱的体积的,则削去部分的体积就是圆柱的体积的 ,削去的部分是8千克,根据分数除法的意义即可求出圆柱的体积.
18.A
解:已修占全长的:
故答案为:A
有量有率,从率入手,修了km后,还剩全长的,则已修的km 占全长的,,所以已修的长。
19.A
解:根据题意,可得
(120-100)÷100
=20÷100
=20%
故答案为:A
要求120比100多百分之几,就是求120比100多的部分占100的百分之几,因此用多出的部分除以100即可。
20.C
解:一共有 (条)直线,这些直线最多共有15×14÷2=105(个)交点,其中原来的6个点中每个点都在5条直线上,这6个点一共充当了 )(个)交点,于是还有105-60=45(个)。
故答案为:C
有n个点,每三个点都不在一条直线上,过其中每两个点画直线,可以画 条直线,每两条直线不重合的话,有且只有1个交点,一共可以形成的交点总数为个交点。 原始的6个点本身,每个点都是5条直线的交点,而每3条直线中至少有2条直线相交于该点,因此,每个点实际上充当了= 5 × 4 ÷2 = 10 个交点,6个点共充当 6 × 10 = 60 个交点。 最后用总的交点数中减去原有点所充当的交点数,就得到实际额外产生最多的交点数
21.D
解:根据题意,可得
3道题的错误选项的各种情况有:
(3×3)×3=27种
27+1=28(人)
故答案为:D
每道题有3个错误选项,所以3道题的错误选项的各种情况有:(3×3)×3=27种。因为至少有两个同学选对、选错的情况完全相同,所以学生人数至少为:27+1=28人。
22.D
解: 通过平移可以得到
故答案为:D
平移不改变图形的大小和形状。
23.A
解:根据题意,可得
由0、1、2这三个数字可以组成的两位数有:10、11、12、20、21、22
10=2×5,
11=11,
12=22×3,
20=22×5,
21=3×7,
22=2×11
因此,最小公倍数为:22×3×5×7×11=4620
故答案为:A
由0、1、2这三个数字可以组成的两位数有:10、11、12、20、21、22。将每个数分解为质因数:10=2×5,11=11,12=22×3,20=22×5,21=3×7,22=2×11,找出所有质因数的最高次幂,确定最小公倍数:2的最高次幂为22,3的最高次幂为3,5的最高次幂为5,7的最高次幂为7,11的最高次幂为11,因此,最小公倍数为:22×3×5×7×11=4620。
24.B
解:最坏情况:
先取2红、2白、2绿,无3个同色,
再取第7个球时,必有3个同色,
因此,最少取出7个球,才能保证3个同色,
故答案为:B
利用最不利原则,最多可取出2个红球、2个白球和2个绿球使得取出的球中不会产生3个颜色相同的球,此时再任意取出一个球,则会出现3个颜色相同的球,因此结果为2×3+1=7(个)。
25.C
解:设平x场,得:
3×(24-x)+2x=22+19+14+12
72-3x+2x=67
x=5
答:有5场比赛为平局.
故答案为:C.
每个队都与其他队交锋4场,总共进行4×3+4×2+4=24场比赛,因为输一场不得分,因此不用去管输的场数.因为平一场双双都得1分,因此平1场共得2分,设平x场,由此列方程为:3×(24-x)+2x=22+19+14+12,解方程即可.
26.D
解:因为池塘里的睡莲的面积每天长大一倍,
所以长满整个池塘的前一天这些睡莲长满半个池塘,13-1=12(天)。
故答案为:D
此题用逆推的方法解答,睡莲的面积每天长大一倍,13天睡莲面积=12 天睡莲面积×2,13 天长满整个池塘,所以12天长满半个池塘。
27.C
解:假设这种商品的成本价是100元;
利润:100×20%=20(元)
现在的成本:100×(1+25%)
=100×1.25
=125(元)
20÷125=16%
即,进价提高后的利润率为16%。
故答案为:C
假设这种商品的成本价是100元,则利润是100×20%=20(元);现在的成本是100×(1+25%)=125(元);要保持利润不变,那么用利润除以现在的成本就是进价提高后的利润率。
28.B
解:根据题意,可得
68×9÷8=76.5(分)
答:平均分最高为76.5分。
故答案为:B
小克的试卷最高100,最低0分。去除最低分让平均分最高需要让最低分等于0,这样用总分除以8就是其他8张试卷的最高平均分。总分为68×9=612(分),其他8张最高平均分为612÷8=76.5
29.B
解:根据题意,可得
=
=
=
循环小数为:,循环节为“63”。
第2016位数字为:2016 2=2014
2014÷2=1007,余数为0。
因此,第2016位数字是循环节中的最后一位,即3。
故答案为:B
先将循环小数 化成分数:,然后再根据题意,,然后化简,再化成循环小数:,确定循环节“63”,确定第2016位的数字2014,在循环节中,2014除以循环节的长度(即2),得到1007余0,据此即可判断循环节中最后一位数
30.C
解:由题意知,丙的成绩是(a+9)分,丁的成绩是(a-3)分,
则他们四人的平均成绩为:
[ 2a+( a+9)+( a-3) ]÷4
=( 4a+6)÷4
=a+1.5,
故答案为:C
先表示出丙的成绩是(a+9)分,丁的成绩是(a-3)分,然后把甲、乙、丙、丁的成绩相加,再除以4,计算即可得解。
31.A
解:3.14÷3.14=1,2÷2=1,A能围成圆柱。
故答案为:A。
要围成圆柱的底面直径=2÷2=1,圆柱的直径=底面周长÷π,两者相等是就能围成圆柱。
32.B
解:温度计所显示的温度是在0度以下是-5℃。
故答案为:B。
正数和负数表示具有相反意义的量;零上温度记作正数,零下温度记作负数, 温度计所显示的温度是在0度以下是-5℃。
33.C
解:A项:2-0=2;
B项:0-(-1)=1;
C项:0.5-0=0.5;
2>1>0.5,0.5与0最接近。
故答案为:C。
分别计算出0与各项数的差,差最小的最接近0。
34.B
解:(厘米),
20000000 厘米=200千米。
故答案为:B
1千米=100000厘米,计算金华到杭州的实际距离,需要利用地图比例尺的知识,根据图上距离与比例尺的关系来求解。
35.B
解:4.2米=42分米,
4.8米=48分米
42=2×3×7,
48=2×2×2×2×3,
所以42和48的最大公因数为:2×3=6。
故答案为:B
要找到不需要切割的方砖边长,需先将客厅的长和宽单位换算成分米,然后找出长和宽的公因数,判断每个选项是否为公因数。
36.B
解:
=9.3×3-9.3
=27.9-9.3
=18.6(立方厘米)
故答案为:B
首先要明确等底等高的圆锥与圆柱体积之间的关系,通过已知圆锥体积求出圆柱体积,再依据两者关系求出削去部分体积,最后根据运算逻辑判断选项。
37.C
解:
=50.24(立方分米)
故答案为:C
根据圆锥体积公式 V= π r2, (π取3.14) ,我们需要将题目中给出的半径和高的值代入公式计算体积,然后与选项进行对比得出答案。
38.A
解:12.56÷(2×3.14)
=12.56÷6.28
=2(cm)
故答案为:A
圆规两脚间的距离就是所画圆的半径。要求这个距离,就需要根据已知的圆周长,利用圆的周长公式来计算半径。
39.C
解:四队的得分为9,7,5,3或者7,5,3,1,据题意可知,乙队的分数只能是7分。
丁队得分为5分,甲队得分为3分,丙队得分为1分。
故答案为:C
一场胜利可以得到3分,则3场比赛最多得到9分,由题知这4支队伍得分为4个连续奇数,且丁队有2场踢平。因此乙队排名第一,得分为7分(如果剩下那场是负的话,丁得分就为偶数);据比赛规则及得分为连续的奇数可知,乙为两胜一平,丁为两平一胜,丙为一平两负,甲为两负一胜,所以丙得分最少。
40.A
解:根据题意,可得
以1为首位的共有: (个)
以2为首位的共有: (个)
共有64+7=71(个)
故答案为:A
以1为首位时,百位、十位、个位三个数位上都可以在2,0,1,3四个数字中任选,共有(4×4×4)种可能。
以2为首位时,百位上只能是0,当十位上是1时个位只能小于3,可选2,0,1,有3种可能。
当十位上是0时,个位就可在2,0,1,3四个数中任选一个,有4种可能。
41.A
解:根据题意,可得
(个)
100-91=9(个)
第100个分数是
故答案为:A
观察这串分数的分母变化规律,分母是n,就有(n-1)个以此为分母的分数,然后计算出分数分母是2~14的分数的个数,即可推出第100 个分数是分母为15 的第9个分数,即
42.B
解:如图
甲:π×(r1+r2)÷2
=
乙:π×r1÷2+π×r2÷2
=
=
因为=,所以甲蜗牛爬行的路线和乙蜗牛爬行的路线长度相等。
假设两条路线的长度均为1。
(1÷6)÷(1÷4)
=
=
=
所以,甲蜗牛的速度是乙蜗牛的。
故答案为:B
根据“C=πd”求出甲爬行路线和乙爬行路线的长度,计算可知,两条路线的长度相等,假设出两条路线的长度,根据“速度=路程÷时间”表示出两只蜗牛的速度,最后用除法求出甲蜗牛的速度占乙蜗牛速度的分率,据此解答。
43.D
解:根据题意,可得
直径:小圆:大圆=1:2,
周长:小圆:大圆=1:2。
故答案为:D
圆的周长=2×圆的半径×π=圆的直径×π,由此可以的得出,两个圆的周长比=两个圆的直径比=两个圆的半径比
44.B
解:在除法运算中,余数总是小于除数。
因为除数是5,所以b可以是1,2,3,4,共有4种可能性。
故答案为:B
在带余除法中,余数必须小于除数,因为除数是5,据此余数必须小于5,据此即可求解
45.B
解:根据题意,可得
如果用+3米表示高出警戒水位3米,那么低于警戒水位5米记作-5
故答案为:B
题目明确指出,高出警戒水位3米用+3米表示。基于此规则,对于低于警戒水位的情况,应该使用负数来表示。根据题目描述,低于警戒水位5米应记作-5米,据此即可求解
46.B
解:15时10分-13时10分=1 小时40分
1 小时40分=100分钟。
故答案为:B
从电影放映时间等于结束时间减去开始时间,然后将结果转换成分钟。 从13:30到14:30,我们经过了一个完整的小时。然后,从14:30到15:10,我们又经过了40分钟。因此,总时间是1小时40分钟, 据此可解。
47.C
解:选项A:根据轴对称的定义,两个图形如果关于某条直线对称,它们的形状和大小必须完全相等,因此A项不正确。
选项B:平移和轴对称都不改变图形的形状和大小,只改变图形的位置,因此B项的描述是错误的。
选项C:准确反映了平移和轴对称的性质,因此C项正确。
选项D:所有长方形都是轴对称图形,因为它们都至少有两条对称轴:一条是通过较长边的中点,另一条是通过较短边的中点。因此D项不正确。
故答案为:C。
(1)轴对称和平移的性质:轴对称是指图形沿某条直线折叠后能完全重合,而平移是指将图形沿着直线方向移动一定距离。两者都不改变图形的大小和形状,只改变图形的位置。
(2)轴对称图形的概念,即存在一条或多条直线,使得图形相对于这条直线折叠时,图形的两部分完全重合。
48.B
解:根据题意,可得,
则 =4,
那么阴影部分面积占正方形面积的
故答案为:
图中阴影部分的面积=大正方形面积-周边3个三角形的面积,阴影部分面积÷正方形面积即可。
49.D
解:首先考虑特殊数字2的位置,当2在左下角时,1如果放置在右下角,4和3 有两种位置。
如果1不放置在右下角的位置,只能放置在紧挨着右下角的两个位置,每种情况都有2种,所以有4种位置。
根据对称性,2在右下角的情况与前相同,则共有:(4+2)×2=12(种)。
答:一共有12种不同的放法.
故答案为:D.
首先考虑特殊的数字2的位置,(1)当2在左下角时,1如果放置在右下角;(2)如果1不放置在右下角的位置;分两类讨论即可,然后2在右下角与前相同.
50.C
解:根据“年份+班号+学号”编号为030415。
故答案为:C
对王刚同学的学籍号进行编排,按照从大范围到小范围的顺序,依次是入学年份、班级、学号。
同课章节目录
