2024-2025学年小升初数学备考真题分类汇编(广东地区专版)专题2 单项选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(广东地区专版)专题2 单项选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 07:28:33 | ||
图片预览




文档简介
专题2 单项选择题-2023-2024学年
小升初数学备考真题分类汇编(广东地区专版)
试卷说明:
本试卷试题精选自广东省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广东省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·天河)+=(a,b,c都是不等于0的自然数),a,b,c中最小的是( )
A.无法确定 B.a C.b D.c
2.(2024·深圳)一个圆柱体的侧面展开图是一个正方形,这个圆柱底面直径与高的比是( )。
A.1:π B.1:2π C.1:4π D.2:π
3.(2024·罗湖)红领巾气象站每两小时要测量一次气温,为了形象地表示出一天中气温的升降变化情况,应当绘制( )统计图最合适。
A.条形 B.复式条形 C.折线 D.复式折线
4.(2024·天河)规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是( )
A.15吨记为+5吨 B.8吨记为﹣8吨
C.6吨记为﹣4吨 D.+3吨表示重量为13吨
5.(2024·广州)在多元智能大赛的决赛中只有三道题。已知:(1)某校25名学生参加竞赛,每个学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍;(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题。那么只解出第二题的学生人数是( )人。
A.5 B.6 C.7 D.8
6.(2024·广州)一种收录机,连续两次降价10%后的售价是405元,那么原价是( )。
A.560元 B.520元 C.500元 D.490元
7.(2024·广州)周长都相等的圆、正方形和长方形,它们的面积相比,( )。
A.圆最大 B.正方形最大 C.长方形最大 D.一样大
8.(2024·电白)“司马光砸缸”是大家熟知的故事,大意是水缸里原有一部分水(未满),玩耍的孩童落入水缸中,水已没过孩童头顶。同伴们除了大声呼救,毫无办法。此时,司马光急中生智,举起石头砸破水缸,水流出后,孩童得救。下面比较符合“司马光砸缸”的故事情节的图是( )
A. B.
C. D.
9.(2024·电白)笑笑把1000元存入银行,定期三年,年利率是2.75%,到期后她准备把利息捐给“希望工程”,她可以捐给“希望工程”( )元。
A.3000 B.27.5 C.1082.5 D.82.5
10.(2024·深圳)小张买了一张入场券,它的号码是四位数,其中个位数是质数,十位数是5的倍数,百位数是偶数,千位数是个位数的3倍,该入场券的号码可能是( )。
A.9303 B.9402 C.9455 D.9853
11.(2024·深圳)用一个放大5倍的放大镜看一个30度的角,放大后看到角的度数是( )。
A.30度 B.150度 C.60度 D.不能确定
12.(2024·东莞)一种食品包装袋上标有“净含量(500±5)克”,质检员随机抽查了5 袋食品,净含量分别是495克,492克,507克,504克,505克,不合格的产品有( )袋。
A.4 B.3 C.2 D.1
13.(2024·东莞)作家格拉德威尔在《异类》中写道:“人们眼中的天才之所以卓越非凡,并非天资超人一等,而是付出了持续不断的努力。”他提出,只要在一个领域持续作出1万小时的努力,就能成为这方面的专家。如果你想练习自己的一项技艺,并想做到出类拔萃,你坚持每天投入2 小时练习,( )年后就可以累积到1万小时。
A.1 B.10 C.14 D.20
14.(2024·广州)正方体的棱长扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
15.(2024·坪山)下面选项中的两种量不成比例关系的是( )
A.苹果的单价一定,购买苹果的数量和总价。
B.正方体的体积与它的棱长。
C.飞机行驶的速度一定,行驶的路程和时间。
D.小麦每公顷产量一定,小麦的总产量与公顷数。
16.(2024·坪山)奇思的爸爸有一个密码箱,他忘记了密码,请你根据提示帮助他找到密码。密码是( )
提示:密码是一个三位数。百位上是最小的质数,十位上的数比百位上的数多3,这个三位数既有因数5,又是3的倍数。
A.140 B.145 C.250 D.255
17.(2024·罗湖) 6的因数有1,2,3,6,这几个因数的关系是1+2+3=6。像6这样,等于除了它自身以外的全部因数之和的数,叫作完全数。下面的数中,( )是完全数。
A.49 B.36 C.28 D.8
18.(2024·南海)如下图,对长方形ABCD的各顶点的位置描述不正确的是( )
A.A点位于(1,5)。 B.B点位于(5,5)。
C.C点在B点的正南方向3cm处。 D.D点在B点的西偏南45°4cm处。
19.(2024·广州)商场以200元/件的成本购进一种商品,并以50%的利润率来定价,但因为价高,无人购买,只好打八五折促销,那么促销后该商品的利润是每件( )元。
A.30 B.40 C.55 D.255
20.(2024·广州)把1 克糖加入10克水中,则糖占糖水的( )。
A. B. C.
21.(2024·雷州)如下图,从镜子中看到的图形是( )
A. B. C.
22.(2024·雷州)要反映近几年来我国居民人均年收入的变化情况及趋势,选择( )统计图最合适。
A.条形 B.折线 C.扇形
23.(2024·广州)某大学从地图上看是一个长方形,画在比例尺是1:5000的平面图上,长是4 cm,宽是3cm。这所大学的实际面积是( )平方米。
A.30000 B.60000 C.300000 D.600000
24.(2024·澄海)一个圆柱形木棒削成一个最大的圆锥体,削掉了这个圆柱的( )
A. B. C. D.
25.(2024·澄海)在一个密封的不透明的袋子里只装了2个红球、2个白球,露露伸手任意抓1个球。抓到红球的可能性是( )
A. B. C. D.无法确定
26.(2024·澄海)把的分母加上6,要使分数值不变,分子应当( )
A.加上6 B.乘2 C.乘6 D.加上14
27.(2024·花都)学校设立“红领巾交换书屋”鼓励学生课外借阅,校长想了解全校学生年阅读量情况。以下 ( )同学介绍的关于书屋的信息对他最有帮助。
A.东东:去年全校人均借阅18.5 本
B.青青: 周一被借出368本
C.红红: 六 (1) 班去年借阅 1023本
D.莎莎:我上周借阅2本
28.(2024·花都)如果把教室的平面图画在一张和数学课本封面大小一样的图纸上,你选择的比例尺是 ( )。
A.100:1 B.1:10 C.1:100 D.1:20000
29.(2024·增城)把一个圆柱底面分成许多相等的扇形,切开后拼成一个近似的长方体。如果圆柱的半径是r,圆柱与长方体相比,下面说法错误的是( )
A.形状变了,体积不变 B.体积不变,表面积不变
C.长方体的长等于πr D.长方体的高等于圆柱的高
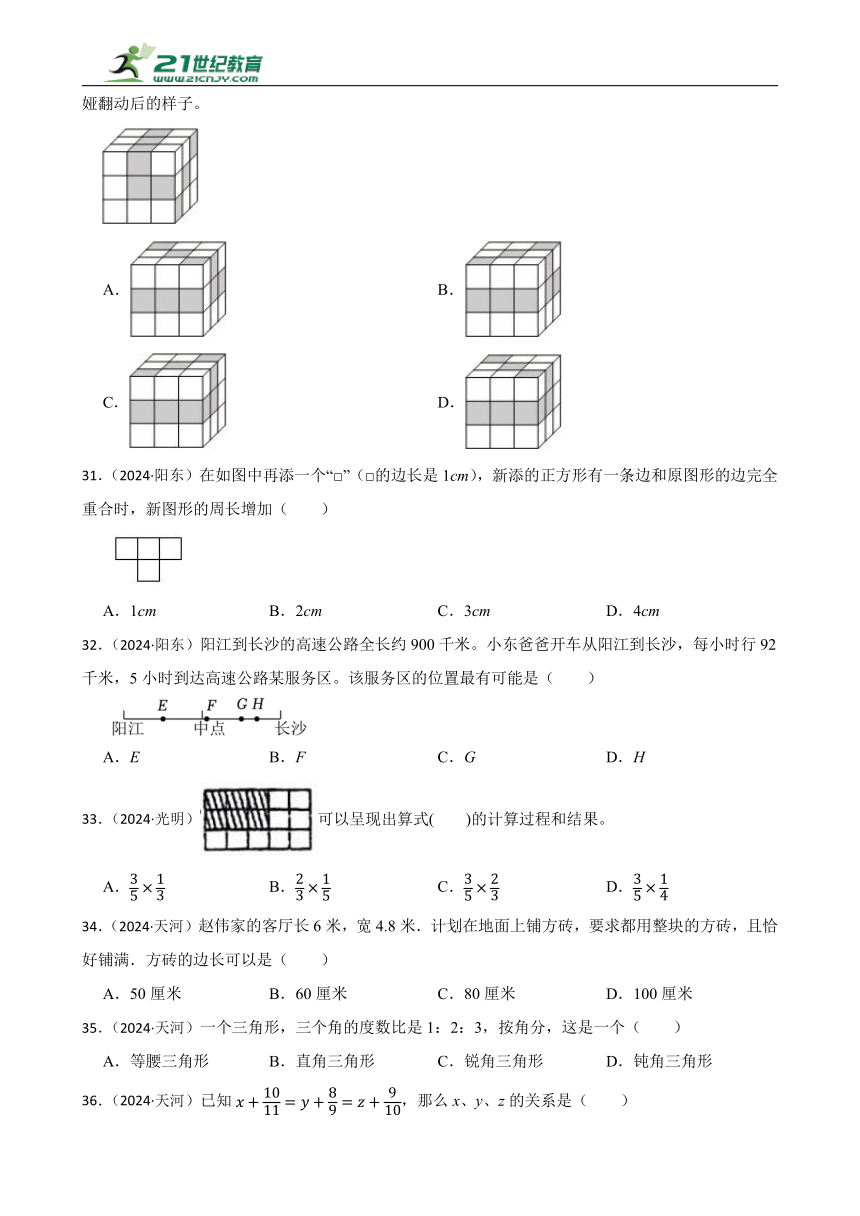
30.(2024·增城)如图是三个面带有图案的正方体,小娅翻动了这个正方体,下面( )可能是小娅翻动后的样子。
A. B.
C. D.
31.(2024·阳东)在如图中再添一个“□”(□的边长是1cm),新添的正方形有一条边和原图形的边完全重合时,新图形的周长增加( )
A.1cm B.2cm C.3cm D.4cm
32.(2024·阳东)阳江到长沙的高速公路全长约900千米。小东爸爸开车从阳江到长沙,每小时行92千米,5小时到达高速公路某服务区。该服务区的位置最有可能是( )
A.E B.F C.G D.H
33.(2024·光明)可以呈现出算式( )的计算过程和结果。
A. B. C. D.
34.(2024·天河)赵伟家的客厅长6米,宽4.8米.计划在地面上铺方砖,要求都用整块的方砖,且恰好铺满.方砖的边长可以是( )
A.50厘米 B.60厘米 C.80厘米 D.100厘米
35.(2024·天河)一个三角形,三个角的度数比是1:2:3,按角分,这是一个( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
36.(2024·天河)已知,那么x、y、z的关系是( )
A.x>z>y B.y>z>x C.x>y>z D.z>x>y
37.(2024·天河)小明每天步行锻炼身体,他小时走了千米。小明步行的速度是( )
A.5千米 B.千米/小时
C.5千米/小时 D.千米/小时
38.(2024·阳东)在出油率、出勤率、合格率、成活率中,不可能达到100%的是( )
A.出油率 B.出勤率 C.合格率 D.成活率
39.(2024·阳东)如图是一个正方体纸盒的展开图,当还原折成纸盒时,与点1重合的点是点( )
A.6和11 B.6和10 C.7和11 D.7和10
40.(2024·增城)如图是一道两位数乘两位数的乘法竖式,把第一次乘得的积记作“甲”,第二次乘得的积记作“乙”,下面图( )能反映甲、乙之间的关系。
A.甲是乙的20% B.乙是甲的20%
C.甲是乙的25% D.乙是甲的25%
41.(2024·增城)如图三幅图分别描述三个故事,这三幅图对应的故事正确的是( )
A.龟兔赛跑、司马光砸缸、乌鸦喝水
B.乌鸦喝水、司马光磁缸、龟兔赛跑
C.司马光砸缸、龟兔赛跑、乌鸦喝水
D.乌鸦喝水、龟兔赛跑、司马光砸缸
42.(2024·增城)点m和点n位置如图所示,下面说法正确的是( )
A.n>m B.mn>m C.>1 D.>1
43.(2024·增城)把一段a米(a>0)长的铁丝平均分成4段,每段铁丝长( )米
A. B. C. D.
44.(2024·花都)根据人体工程学的研究发现,人的两只眼睛的视野范围是一个长与宽的比为16:9的长方形,所以电视、显示器行业根据这个比设计产品,下面对长与宽的比为16:9的长方形理解正确的是( )。
①宽是长的 ②宽比长短 ③长是宽的 ④长比宽长
A.①③ B.①②③ C.①③④ D.①②③④
45.(2024·花都)张老师要买54个足球,三个店的足球单价都是48元,但促销方式各不相同。张老师到( )店买更合算。
1号店:每买10个送3个;
2号店:打七折销售;
3号店:购物每满200元,返现金50元。
A.1号 B.2号 C.3号 D.无法确定
46.(2024·广州)有6张电影票如图所示,撕成相连的3张,共有( )种不同的撕法。
A.10 B.8 C.6 D.4
47.(2024·广州)A,B两地相距2400米,甲从A地,乙从B地同时出发,在A,B两地往返长跑,每分钟甲跑300米,乙跑240米,35分钟后停止。甲、乙在第( )次相遇距A最近。
A.1 B.2 C.3 D.4
48.(2024·广州)把若干个棱长为1厘米的小正方体木块搭成一个立体图形,从上面和前面看到的都是如图所示的图形,搭这个立体图形最多需要 个这样的小正方体,最少需要 个这样的小正方体。
A. 9 B. 8 C. 7 D. 5
49.(2024·广州)用汽车运一批货,要求每次运走的一样多,已经运了5次,运走的货物比 多一些,比 少一些,运完这批货物最多要运( )次。
A.8 B.9 C.10 D.11
50.(2024·广州)一个奇怪的动物庄园里住着猫和狗,狗比猫多180 只,有20%的狗错认为自己是猫;有20%的猫错认为自己是狗。在所有的猫和狗中,有32%认为自己是猫,那么狗有( )只。
A.240 B.24 C.420 D.842
答案解析部分
1.D
解:+= 这三个份数的分子相同,则> ,则c<a,>,则c<b,最小的是c。
故答案为:D。
两个数的和一定大于不为0的任意一个加数,分子相等的分数,分母大的反而小,得出最小的是c。
2.A
解:设这个圆柱底面直径为d,因为圆柱体的侧面展开图是一个正方形,所以圆柱的高为πd,那么圆柱底面直径与高的比是d:πd=1:π。
故答案为:A
圆柱体的侧面展开图是正方形,说明圆柱体的高等于圆柱底面周长。
3.C
解:折线统计图能清楚地看出数量的增减变化情况,所以为了形象地表示出一天中气温的升降变化情况,应当绘制折线统计图最合适。
故答案为:C。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况;扇形统计图能反应各个部分占总体的百分之几。
4.B
解:A项:15-10=5(吨),记作+5吨;
B项:8-10=-2(吨),记作-2吨;
C项:6-10=-4(吨),记作-4吨;
D项:10+3=13(吨)。
故答案为:B。
正数和负数表示具有相反意义的量;高于10吨的记作正数,低于10吨的记作负数。
5.B
6.C
解:根据题意,可得
405÷(1-10%)÷(1-10%)
=405÷90%÷90%
=500(元)。
答:原价是500元
故答案为:C
用405除以(1-10%)先算出第一次降价的售价,然后再第一次降价的基础上再除以(1-10%),即可求解
7.A
解:设正方形、长方形、圆的周长都是16厘米,则:
正方形的边长:16÷4=4(厘米),面积:4×4=16(平方厘米);
假设长方形的长为6厘米,宽为2厘米,则面积:2×6=12(平方厘米);
圆的半径:16÷3.14÷2=8÷3.14≈2.5(厘米),面积:3.14×2.52=3.14×6.25=19.625(平方厘米);
所以周长相等的正方形、长方形和圆,圆的面积最大。
故答案为:A周长相等的图形中,圆的面积最大。要进行验证,可以设正方形、长方形、圆的周长为一个具体的数值,一次对三个图形的面积进行计算和比较。
8.C
解:由题意可知,水面高度刚开始不变,当玩耍的孩童落入水缸中,水面高度上升,而后水面高度不变,当司马光将缸砸破后,水面高度逐渐下降。
故答案为:C。
掌握折线统计图的特征是解题的关键。统计图的纵轴表示水缸里的水面高度,横轴表示时间;水缸里原有一部分水,就是水面有一定的高度,保持不变;玩耍的孩童落入水缸中,水已没过孩童头顶,这时水缸的水面高度是上升状态;同伴们除了大声呼救,毫无办法,这时水缸里的水上升到最高后保持不变;司马光急中生智,举起石头砸破水缸,水流出后,这时水缸里的水逐渐减少,水面高度逐渐下降;据此解答。
9.D
解:1000×2.75%×3=82.5(元)
故答案为:D。
本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。根据利息=本金×利率×存期,代入数值进行计算即可。
10.D
解:个位是质数有:2、3、5、7;
十位是5的倍数有:0或5;
百位是偶数有:0、2、4、6、8;
千位是4的倍数有:3、6、9;
因为个位是质数,且千位上的数是个位上数的3倍,由此可知这个四位数是:9853。
故答案为:D。
根据质数、偶数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;是2的倍数的数叫做偶数;以及倍数的含义,据此解答即可。
11.A
解:不管用放大多少倍的放大镜看一个30度的角,这个角始终是30度。
故答案为:A
角的大小取决于角两边张开的程度,与边的长度无关。放大镜放大的只是边的长度,而不是角两边张开的程度,所以用放大镜看角角的度数是不会改变的。
12.C
解:根据题意得,合格的范围是495g~505g,
即超过505g和低于495g为不合格,
则有2袋不合格.
故答案为:C
根据题意可知“500±5g”表示在500g左右有5g的误差,即含量为495g~505g的都是合格产品,即不合格的为492g和507g,即2袋不合格.
13.C
解:根据题意,可得
10000÷2÷365≈14(年)
故答案为:C
根据总时间÷每天时间=天数,天数÷365≈年数。代入数据即可求解
14.D
解:正方体棱长扩大到原来的2倍,体积扩大到原来的 倍。
故答案为:D
正方体棱长扩大到原来的n倍,体积会扩大到原来的 倍。正方体的体积=棱长×棱长×棱长
15.B
解:A项:总价÷数量=单价(一定),苹果的单价一定,购买苹果的数量和总价成正比例;
B项:正方体的体积=棱长×棱长×棱长,正方体的体积与它的棱长不成比例;
C项:路程÷时间=速度(一定),飞机行驶的速度一定,行驶的路程和时间成正比例;
D项:小麦的总产量÷公顷数=小麦每公顷产量(一定)小麦每公顷产量一定,小麦的总产量与公顷数 成正比例。
故答案为:B。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
16.D
解:百位上是最小的质数2,十位上的数比百位上的数多3,3+2=5,这个三位数既有因数5,又是3的倍数,个位数字是5,这个密码是255。
故答案为:D。
最小的质数是2,十位上的数=百位上的数+3=5,个位上的数是5,这个密码是255。
17.C
解:28的因数有1、28、2、14、4、7;
1+2+4+7+14=28。
故答案为:C。
先写出28的所有因数,并且除了28以外所有因数的和等于28。
18.D
解:A项:A点在第1列,第5行,用数对表示(1,5) ,原题干说法正确;
B项:B点在第5列,第5行,用数对表示(5,5) ,原题干说法正确;
C项:C点在B点的正南方向3cm处 ,原题干说法正确;
D项:D点在B点的西偏南45°>4cm处,原题干说法错误。
故答案为:D。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对,直角三角形斜边的长度大于直角边的长度。
19.C
解:200×(1+50%)×85% - 200
=300×0.85-200
=255-200
=55(元)
故答案为:C
售价-进价=盈利
20.C
解:
故答案为:C
求出糖水质量是糖的质量与水的质量之和,再根据糖的质量与糖水质量求出糖占糖水的比例。
21.C
解:根据镜面对称的特征可知,从镜子中看到的图形是。
故答案为:C。
镜面对称中图形的左右方向相反,上下方向不变。
22.B
解:要反映近几年来我国居民人均年收入的变化情况及趋势,选择折线统计图。
故答案为:B。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。
23.A
解:根据题意,可得
(厘米)=200(米):
(厘米)=150(米),
200×150=30000(平方米)
故答案为:A
根据实际距离=图上距离÷比例尺,分别算出长和宽的实际距离,然后再将厘米化成米,最后再根据面积公式:长×宽,代入数据即可求解
24.B
解:1-=,一个圆柱形木棒削成一个最大的圆锥体,削掉了这个圆柱的。
故答案为:B。
等底等高的圆柱的体积是圆锥的体积的3倍,所以一个圆柱形木棒削成一个最大的圆锥体,削掉了这个圆柱的。
25.C
解:2÷(2+2)
=2÷4
=
故答案为:C。
露露伸手任意抓1个球。抓到红球的可能性=1÷(红球的个数+白球的个数)。
26.D
解:(3+6)÷3
=9÷3
=2
7×3-7
=21-7
=14,分子应当加上14。
故答案为:D。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
27.A
解:A:用人均借阅的本数乘总人数就可以了解全年的阅读量,有帮助;
B:只知道周一借出的本数不能了解全年的阅读量,没有帮助;
C:不同年级的借阅量不相同,不能只根据一个班的借阅量确定全校的借阅量,没有帮助;
D:一个人上周借阅的本数与全校的阅读量无关。
故答案为:A。
了解全校学生的阅读量有多种方法,根据每个选项中给出的条件分析,然后确定能了解全校阅读量的方法即可。
28.C
解:A:100:1的比例尺是放大的比例尺,不合适;
B:1:10表示实际距离缩小了10倍,不合适;
C:1:100表示实际距离缩小了100倍,合适;
D:1:20000表示把实际距离缩小了20000倍,不合适。
故答案为:C。
比例尺表示图上距离与实际距离的比。教室实际的长大约10米,缩小100倍是10厘米,所以1:100的比例尺比较合适。
29.B
解:A:形状变了,体积不变,正确;
B:体积不变,表面积变大,原来说法错误;
C:长方体的长等于底面周长的一半,就是πr,正确;
D:长方体的高等于圆柱的高,正确。
故答案为:B。
按照这种方法拼成近似长方体后,体积不变,表面积比原来增加了左右两个长方形的面;长方体的长就是圆柱的底面周长,宽是圆柱的底面半径,高是圆柱的高。
30.C
解: 将原来的正方体向左翻转一个面后的图形。
故答案为:C。
观察原来图形的右面,刚好在C项中上面,其余两个面也相对应。
31.B
解:在如图中再添一个“□”(□的边长是1cm),新添的正方形有一条边和原图形的边完全重合时,新图形的周长增加2cm。
故答案为:B。
因为只有一条边和原图形的边完全重合,所以周长会减少2条重合的边,因为正方形有4条边,所以周长只增加了2条小正方形的边长。
32.B
解:92×5≈450(千米),所以该服务区的位置最有可能是中点F。
故答案为:B。
用每小时行的路程乘时间求出5小时行驶的路程,然后根据行驶的路程和总路程确定该服务区的位置即可。
33.C
解:可以呈现出算式的计算过程和结果。
故答案为:C。
先把整个图形平均分成5份,其中的3份涂浅色表示;又把涂色部分平均分成3份,给其中的2份涂重色就表示。
34.B
解:6米=60分米,4.8米=48分米
60和48的最大公因数是2×2×3=12,也就是方砖的边长最大是12分米
12分米=120厘米,四个选项中,只有60厘米是120厘米的因数。
故答案为:B。
先用短除法求出赵伟家客厅长、宽的最大公因数是12,也就是12分米=120厘米,观察4个选项中是120的因数的即可。
35.B
解:180÷(1+2+3)×3
=180÷6×3
=30×3
=90(度),这个是直角三角形。
故答案为:B。
这个三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数。
36.B
解:
因为>>,所以x<z<y。
故答案为:B。
两个数相加的和相等,较小的数要加上较大的数。
37.C
解:÷=5(千米/时)。
故答案为:C。
速度=行驶的路程÷用的时间。
38.A
解:在出油率、出勤率、合格率、成活率中,不可能达到100%的是出油率。
故答案为:A。
出勤率、合格率和成活率都有可能达到100%,但不会超过100%;出油率是一定不会达到100%。
39.C
解:如图是一个正方体纸盒的展开图,当还原折成纸盒时,与点1重合的点是点7和11。
故答案为:C。
假设一个面是底面,然后确定前后面,左右面、上下面,然后确定与1重合的点即可。
40.C
解:5÷20=25%,表示甲是乙的25%。
故答案为:C。
甲是第一个因数与5的乘积,乙是第一个因数与20的乘积,乙一定大于甲,用5除以20即可求出甲是乙的百分之几。
41.A
解:第一幅图:图中两条直线,应该表示两种情况,所以应该表示龟兔赛跑;
第二幅图:表示一种元素,且线呈下降趋势,应该是表示司马光砸缸中水的高度不断下降;
第三幅图:表示一种元素,且线呈上升趋势,应该是表示乌鸦喝水中水面的高度不断上升。
故答案为:A。
用折线表示元素的变化情况,两条折线就表示两种元素,折线上升和下降表示的意义是不同的。
42.D
解:A:n<m,所以错误;
B:mn无法和m比较大小,错误;
C:m>1,所以<1,错误;
D:>1,正确。
故答案为:D。
0<n<1,1<m<2,分母大于分子的分数都小于1,分母小于分子的分数都大于1。
43.A
解:a÷4=(米)
故答案为:A。
用这段铁丝的长度除以平均分的段数,用分数表示出每段铁丝的长度即可。
44.C
解:①宽是长的9÷16=,正确;
②宽比长短(16-9)÷16=,错误;
③长是宽的16÷9=,正确;
④长比宽长(16-9)÷9=,正确。
故答案为:C。
把长看作16,宽看作9,用长除以宽即可求出长是宽的几分之几;用宽除以长即可求出宽是长的几分之几;用长与宽的差除以长即可求出宽比长短几分之几;用长与宽的差除以宽即可求出长比宽长几分之几。
45.B
解:1号店:54÷10=5(组)······4(个)
(54-5×3)×48
=39×48
=1872(元);
2号店:54×48×70%
=2592×70%
=1814.4(元)
3号店:54×48=2592(元)
2592÷200=12(组)······192(元)
2592-12×50
=2592-600
=1992(元)
1814.4<1872<1992。
故答案为:B。
1号店总价=(要买的个数-送的个数)×单价;
2号店总价=单价×数量×折扣;
3号店总价=单价×数量-减免的钱数,然后比较大小。
46.A
解:如图所示:
第一类:形如的有2种,
第二类:形如有8种
所以共有:2+8=10(种)
故答案为:A
可以分成两类,第一类,分成两个长方形,第二类,分成两个不规则图形,分别数出各类的数量,相加得到总数。
47.D
解:(300+240)×35=18900(m)
18900÷2400=7(全长)……2100(m).
迎面相遇(7+1)÷2=4(次)
t一定
第1次相遇,共走1全长 (全长),离A地有 全长。
第2次相遇,共走3全长 (全长),离A 地有 全长。
第3次相遇,共走5全长 (全长),离A 地有 全长,
第4次相遇,共走7全长, (全长),离A 地有 全长。
则第4次相遇离A地最近。
故答案为:D。
先用速度和乘时间求出甲、乙所走总路程,然后根据全长求出相遇次数,再根据相遇次数依次求出距A地距离再比较。
48.A;C
把若干个棱长为1厘米的小正方体木块搭成一个图形,从上面和前面看到的都是如图所示那样,搭成这这个图形最多需要9个,最少需要7个这样的小正方体;
最多为
共2×4+1=9(个)
最少为
或或,共2×2+1×3=7(个)。
故答案为:A,C.
把若干个棱长为1厘米的小正方体木块搭成一个图形,从上面和前面看到的都是如图所示那样,它下层有5个小正方体,分成2行,前行3个,后行2个,左对齐,上层4个或2个,若4个,分别在下层左边4个小正方体的上边,若2个,在下层左边4个小正方体的上边,前后不成一行即可,因此,搭成这这个图形最多需要9个,最少需要7个这样的小正方体.
49.A
解:(次)
(次)
则所运次数应大于6 次,小于8 次,满足条件的次数为7次或8次,最多应为8次。
故答案为:A。
先根据已运次数和对应分率求出总次数的范围,再结合问题分析最值。
50.A
解:20%的狗认为自己是猫,20%的猫认为自己是狗,则80%的猫认为自己是猫,而所有动物中,有32%认为自己是猫。
48%:12%=4:1,则狗:猫=4:1
狗:180÷(4-1)×4=240(只)
故答案为:A。
应用“十字交叉法”求出两种动物的数量比,再根据数量差和比例关系列式计算。
小升初数学备考真题分类汇编(广东地区专版)
试卷说明:
本试卷试题精选自广东省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广东省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·天河)+=(a,b,c都是不等于0的自然数),a,b,c中最小的是( )
A.无法确定 B.a C.b D.c
2.(2024·深圳)一个圆柱体的侧面展开图是一个正方形,这个圆柱底面直径与高的比是( )。
A.1:π B.1:2π C.1:4π D.2:π
3.(2024·罗湖)红领巾气象站每两小时要测量一次气温,为了形象地表示出一天中气温的升降变化情况,应当绘制( )统计图最合适。
A.条形 B.复式条形 C.折线 D.复式折线
4.(2024·天河)规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是( )
A.15吨记为+5吨 B.8吨记为﹣8吨
C.6吨记为﹣4吨 D.+3吨表示重量为13吨
5.(2024·广州)在多元智能大赛的决赛中只有三道题。已知:(1)某校25名学生参加竞赛,每个学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍;(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题。那么只解出第二题的学生人数是( )人。
A.5 B.6 C.7 D.8
6.(2024·广州)一种收录机,连续两次降价10%后的售价是405元,那么原价是( )。
A.560元 B.520元 C.500元 D.490元
7.(2024·广州)周长都相等的圆、正方形和长方形,它们的面积相比,( )。
A.圆最大 B.正方形最大 C.长方形最大 D.一样大
8.(2024·电白)“司马光砸缸”是大家熟知的故事,大意是水缸里原有一部分水(未满),玩耍的孩童落入水缸中,水已没过孩童头顶。同伴们除了大声呼救,毫无办法。此时,司马光急中生智,举起石头砸破水缸,水流出后,孩童得救。下面比较符合“司马光砸缸”的故事情节的图是( )
A. B.
C. D.
9.(2024·电白)笑笑把1000元存入银行,定期三年,年利率是2.75%,到期后她准备把利息捐给“希望工程”,她可以捐给“希望工程”( )元。
A.3000 B.27.5 C.1082.5 D.82.5
10.(2024·深圳)小张买了一张入场券,它的号码是四位数,其中个位数是质数,十位数是5的倍数,百位数是偶数,千位数是个位数的3倍,该入场券的号码可能是( )。
A.9303 B.9402 C.9455 D.9853
11.(2024·深圳)用一个放大5倍的放大镜看一个30度的角,放大后看到角的度数是( )。
A.30度 B.150度 C.60度 D.不能确定
12.(2024·东莞)一种食品包装袋上标有“净含量(500±5)克”,质检员随机抽查了5 袋食品,净含量分别是495克,492克,507克,504克,505克,不合格的产品有( )袋。
A.4 B.3 C.2 D.1
13.(2024·东莞)作家格拉德威尔在《异类》中写道:“人们眼中的天才之所以卓越非凡,并非天资超人一等,而是付出了持续不断的努力。”他提出,只要在一个领域持续作出1万小时的努力,就能成为这方面的专家。如果你想练习自己的一项技艺,并想做到出类拔萃,你坚持每天投入2 小时练习,( )年后就可以累积到1万小时。
A.1 B.10 C.14 D.20
14.(2024·广州)正方体的棱长扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
15.(2024·坪山)下面选项中的两种量不成比例关系的是( )
A.苹果的单价一定,购买苹果的数量和总价。
B.正方体的体积与它的棱长。
C.飞机行驶的速度一定,行驶的路程和时间。
D.小麦每公顷产量一定,小麦的总产量与公顷数。
16.(2024·坪山)奇思的爸爸有一个密码箱,他忘记了密码,请你根据提示帮助他找到密码。密码是( )
提示:密码是一个三位数。百位上是最小的质数,十位上的数比百位上的数多3,这个三位数既有因数5,又是3的倍数。
A.140 B.145 C.250 D.255
17.(2024·罗湖) 6的因数有1,2,3,6,这几个因数的关系是1+2+3=6。像6这样,等于除了它自身以外的全部因数之和的数,叫作完全数。下面的数中,( )是完全数。
A.49 B.36 C.28 D.8
18.(2024·南海)如下图,对长方形ABCD的各顶点的位置描述不正确的是( )
A.A点位于(1,5)。 B.B点位于(5,5)。
C.C点在B点的正南方向3cm处。 D.D点在B点的西偏南45°4cm处。
19.(2024·广州)商场以200元/件的成本购进一种商品,并以50%的利润率来定价,但因为价高,无人购买,只好打八五折促销,那么促销后该商品的利润是每件( )元。
A.30 B.40 C.55 D.255
20.(2024·广州)把1 克糖加入10克水中,则糖占糖水的( )。
A. B. C.
21.(2024·雷州)如下图,从镜子中看到的图形是( )
A. B. C.
22.(2024·雷州)要反映近几年来我国居民人均年收入的变化情况及趋势,选择( )统计图最合适。
A.条形 B.折线 C.扇形
23.(2024·广州)某大学从地图上看是一个长方形,画在比例尺是1:5000的平面图上,长是4 cm,宽是3cm。这所大学的实际面积是( )平方米。
A.30000 B.60000 C.300000 D.600000
24.(2024·澄海)一个圆柱形木棒削成一个最大的圆锥体,削掉了这个圆柱的( )
A. B. C. D.
25.(2024·澄海)在一个密封的不透明的袋子里只装了2个红球、2个白球,露露伸手任意抓1个球。抓到红球的可能性是( )
A. B. C. D.无法确定
26.(2024·澄海)把的分母加上6,要使分数值不变,分子应当( )
A.加上6 B.乘2 C.乘6 D.加上14
27.(2024·花都)学校设立“红领巾交换书屋”鼓励学生课外借阅,校长想了解全校学生年阅读量情况。以下 ( )同学介绍的关于书屋的信息对他最有帮助。
A.东东:去年全校人均借阅18.5 本
B.青青: 周一被借出368本
C.红红: 六 (1) 班去年借阅 1023本
D.莎莎:我上周借阅2本
28.(2024·花都)如果把教室的平面图画在一张和数学课本封面大小一样的图纸上,你选择的比例尺是 ( )。
A.100:1 B.1:10 C.1:100 D.1:20000
29.(2024·增城)把一个圆柱底面分成许多相等的扇形,切开后拼成一个近似的长方体。如果圆柱的半径是r,圆柱与长方体相比,下面说法错误的是( )
A.形状变了,体积不变 B.体积不变,表面积不变
C.长方体的长等于πr D.长方体的高等于圆柱的高
30.(2024·增城)如图是三个面带有图案的正方体,小娅翻动了这个正方体,下面( )可能是小娅翻动后的样子。
A. B.
C. D.
31.(2024·阳东)在如图中再添一个“□”(□的边长是1cm),新添的正方形有一条边和原图形的边完全重合时,新图形的周长增加( )
A.1cm B.2cm C.3cm D.4cm
32.(2024·阳东)阳江到长沙的高速公路全长约900千米。小东爸爸开车从阳江到长沙,每小时行92千米,5小时到达高速公路某服务区。该服务区的位置最有可能是( )
A.E B.F C.G D.H
33.(2024·光明)可以呈现出算式( )的计算过程和结果。
A. B. C. D.
34.(2024·天河)赵伟家的客厅长6米,宽4.8米.计划在地面上铺方砖,要求都用整块的方砖,且恰好铺满.方砖的边长可以是( )
A.50厘米 B.60厘米 C.80厘米 D.100厘米
35.(2024·天河)一个三角形,三个角的度数比是1:2:3,按角分,这是一个( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
36.(2024·天河)已知,那么x、y、z的关系是( )
A.x>z>y B.y>z>x C.x>y>z D.z>x>y
37.(2024·天河)小明每天步行锻炼身体,他小时走了千米。小明步行的速度是( )
A.5千米 B.千米/小时
C.5千米/小时 D.千米/小时
38.(2024·阳东)在出油率、出勤率、合格率、成活率中,不可能达到100%的是( )
A.出油率 B.出勤率 C.合格率 D.成活率
39.(2024·阳东)如图是一个正方体纸盒的展开图,当还原折成纸盒时,与点1重合的点是点( )
A.6和11 B.6和10 C.7和11 D.7和10
40.(2024·增城)如图是一道两位数乘两位数的乘法竖式,把第一次乘得的积记作“甲”,第二次乘得的积记作“乙”,下面图( )能反映甲、乙之间的关系。
A.甲是乙的20% B.乙是甲的20%
C.甲是乙的25% D.乙是甲的25%
41.(2024·增城)如图三幅图分别描述三个故事,这三幅图对应的故事正确的是( )
A.龟兔赛跑、司马光砸缸、乌鸦喝水
B.乌鸦喝水、司马光磁缸、龟兔赛跑
C.司马光砸缸、龟兔赛跑、乌鸦喝水
D.乌鸦喝水、龟兔赛跑、司马光砸缸
42.(2024·增城)点m和点n位置如图所示,下面说法正确的是( )
A.n>m B.mn>m C.>1 D.>1
43.(2024·增城)把一段a米(a>0)长的铁丝平均分成4段,每段铁丝长( )米
A. B. C. D.
44.(2024·花都)根据人体工程学的研究发现,人的两只眼睛的视野范围是一个长与宽的比为16:9的长方形,所以电视、显示器行业根据这个比设计产品,下面对长与宽的比为16:9的长方形理解正确的是( )。
①宽是长的 ②宽比长短 ③长是宽的 ④长比宽长
A.①③ B.①②③ C.①③④ D.①②③④
45.(2024·花都)张老师要买54个足球,三个店的足球单价都是48元,但促销方式各不相同。张老师到( )店买更合算。
1号店:每买10个送3个;
2号店:打七折销售;
3号店:购物每满200元,返现金50元。
A.1号 B.2号 C.3号 D.无法确定
46.(2024·广州)有6张电影票如图所示,撕成相连的3张,共有( )种不同的撕法。
A.10 B.8 C.6 D.4
47.(2024·广州)A,B两地相距2400米,甲从A地,乙从B地同时出发,在A,B两地往返长跑,每分钟甲跑300米,乙跑240米,35分钟后停止。甲、乙在第( )次相遇距A最近。
A.1 B.2 C.3 D.4
48.(2024·广州)把若干个棱长为1厘米的小正方体木块搭成一个立体图形,从上面和前面看到的都是如图所示的图形,搭这个立体图形最多需要 个这样的小正方体,最少需要 个这样的小正方体。
A. 9 B. 8 C. 7 D. 5
49.(2024·广州)用汽车运一批货,要求每次运走的一样多,已经运了5次,运走的货物比 多一些,比 少一些,运完这批货物最多要运( )次。
A.8 B.9 C.10 D.11
50.(2024·广州)一个奇怪的动物庄园里住着猫和狗,狗比猫多180 只,有20%的狗错认为自己是猫;有20%的猫错认为自己是狗。在所有的猫和狗中,有32%认为自己是猫,那么狗有( )只。
A.240 B.24 C.420 D.842
答案解析部分
1.D
解:+= 这三个份数的分子相同,则> ,则c<a,>,则c<b,最小的是c。
故答案为:D。
两个数的和一定大于不为0的任意一个加数,分子相等的分数,分母大的反而小,得出最小的是c。
2.A
解:设这个圆柱底面直径为d,因为圆柱体的侧面展开图是一个正方形,所以圆柱的高为πd,那么圆柱底面直径与高的比是d:πd=1:π。
故答案为:A
圆柱体的侧面展开图是正方形,说明圆柱体的高等于圆柱底面周长。
3.C
解:折线统计图能清楚地看出数量的增减变化情况,所以为了形象地表示出一天中气温的升降变化情况,应当绘制折线统计图最合适。
故答案为:C。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况;扇形统计图能反应各个部分占总体的百分之几。
4.B
解:A项:15-10=5(吨),记作+5吨;
B项:8-10=-2(吨),记作-2吨;
C项:6-10=-4(吨),记作-4吨;
D项:10+3=13(吨)。
故答案为:B。
正数和负数表示具有相反意义的量;高于10吨的记作正数,低于10吨的记作负数。
5.B
6.C
解:根据题意,可得
405÷(1-10%)÷(1-10%)
=405÷90%÷90%
=500(元)。
答:原价是500元
故答案为:C
用405除以(1-10%)先算出第一次降价的售价,然后再第一次降价的基础上再除以(1-10%),即可求解
7.A
解:设正方形、长方形、圆的周长都是16厘米,则:
正方形的边长:16÷4=4(厘米),面积:4×4=16(平方厘米);
假设长方形的长为6厘米,宽为2厘米,则面积:2×6=12(平方厘米);
圆的半径:16÷3.14÷2=8÷3.14≈2.5(厘米),面积:3.14×2.52=3.14×6.25=19.625(平方厘米);
所以周长相等的正方形、长方形和圆,圆的面积最大。
故答案为:A周长相等的图形中,圆的面积最大。要进行验证,可以设正方形、长方形、圆的周长为一个具体的数值,一次对三个图形的面积进行计算和比较。
8.C
解:由题意可知,水面高度刚开始不变,当玩耍的孩童落入水缸中,水面高度上升,而后水面高度不变,当司马光将缸砸破后,水面高度逐渐下降。
故答案为:C。
掌握折线统计图的特征是解题的关键。统计图的纵轴表示水缸里的水面高度,横轴表示时间;水缸里原有一部分水,就是水面有一定的高度,保持不变;玩耍的孩童落入水缸中,水已没过孩童头顶,这时水缸的水面高度是上升状态;同伴们除了大声呼救,毫无办法,这时水缸里的水上升到最高后保持不变;司马光急中生智,举起石头砸破水缸,水流出后,这时水缸里的水逐渐减少,水面高度逐渐下降;据此解答。
9.D
解:1000×2.75%×3=82.5(元)
故答案为:D。
本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。根据利息=本金×利率×存期,代入数值进行计算即可。
10.D
解:个位是质数有:2、3、5、7;
十位是5的倍数有:0或5;
百位是偶数有:0、2、4、6、8;
千位是4的倍数有:3、6、9;
因为个位是质数,且千位上的数是个位上数的3倍,由此可知这个四位数是:9853。
故答案为:D。
根据质数、偶数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;是2的倍数的数叫做偶数;以及倍数的含义,据此解答即可。
11.A
解:不管用放大多少倍的放大镜看一个30度的角,这个角始终是30度。
故答案为:A
角的大小取决于角两边张开的程度,与边的长度无关。放大镜放大的只是边的长度,而不是角两边张开的程度,所以用放大镜看角角的度数是不会改变的。
12.C
解:根据题意得,合格的范围是495g~505g,
即超过505g和低于495g为不合格,
则有2袋不合格.
故答案为:C
根据题意可知“500±5g”表示在500g左右有5g的误差,即含量为495g~505g的都是合格产品,即不合格的为492g和507g,即2袋不合格.
13.C
解:根据题意,可得
10000÷2÷365≈14(年)
故答案为:C
根据总时间÷每天时间=天数,天数÷365≈年数。代入数据即可求解
14.D
解:正方体棱长扩大到原来的2倍,体积扩大到原来的 倍。
故答案为:D
正方体棱长扩大到原来的n倍,体积会扩大到原来的 倍。正方体的体积=棱长×棱长×棱长
15.B
解:A项:总价÷数量=单价(一定),苹果的单价一定,购买苹果的数量和总价成正比例;
B项:正方体的体积=棱长×棱长×棱长,正方体的体积与它的棱长不成比例;
C项:路程÷时间=速度(一定),飞机行驶的速度一定,行驶的路程和时间成正比例;
D项:小麦的总产量÷公顷数=小麦每公顷产量(一定)小麦每公顷产量一定,小麦的总产量与公顷数 成正比例。
故答案为:B。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
16.D
解:百位上是最小的质数2,十位上的数比百位上的数多3,3+2=5,这个三位数既有因数5,又是3的倍数,个位数字是5,这个密码是255。
故答案为:D。
最小的质数是2,十位上的数=百位上的数+3=5,个位上的数是5,这个密码是255。
17.C
解:28的因数有1、28、2、14、4、7;
1+2+4+7+14=28。
故答案为:C。
先写出28的所有因数,并且除了28以外所有因数的和等于28。
18.D
解:A项:A点在第1列,第5行,用数对表示(1,5) ,原题干说法正确;
B项:B点在第5列,第5行,用数对表示(5,5) ,原题干说法正确;
C项:C点在B点的正南方向3cm处 ,原题干说法正确;
D项:D点在B点的西偏南45°>4cm处,原题干说法错误。
故答案为:D。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对,直角三角形斜边的长度大于直角边的长度。
19.C
解:200×(1+50%)×85% - 200
=300×0.85-200
=255-200
=55(元)
故答案为:C
售价-进价=盈利
20.C
解:
故答案为:C
求出糖水质量是糖的质量与水的质量之和,再根据糖的质量与糖水质量求出糖占糖水的比例。
21.C
解:根据镜面对称的特征可知,从镜子中看到的图形是。
故答案为:C。
镜面对称中图形的左右方向相反,上下方向不变。
22.B
解:要反映近几年来我国居民人均年收入的变化情况及趋势,选择折线统计图。
故答案为:B。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。
23.A
解:根据题意,可得
(厘米)=200(米):
(厘米)=150(米),
200×150=30000(平方米)
故答案为:A
根据实际距离=图上距离÷比例尺,分别算出长和宽的实际距离,然后再将厘米化成米,最后再根据面积公式:长×宽,代入数据即可求解
24.B
解:1-=,一个圆柱形木棒削成一个最大的圆锥体,削掉了这个圆柱的。
故答案为:B。
等底等高的圆柱的体积是圆锥的体积的3倍,所以一个圆柱形木棒削成一个最大的圆锥体,削掉了这个圆柱的。
25.C
解:2÷(2+2)
=2÷4
=
故答案为:C。
露露伸手任意抓1个球。抓到红球的可能性=1÷(红球的个数+白球的个数)。
26.D
解:(3+6)÷3
=9÷3
=2
7×3-7
=21-7
=14,分子应当加上14。
故答案为:D。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
27.A
解:A:用人均借阅的本数乘总人数就可以了解全年的阅读量,有帮助;
B:只知道周一借出的本数不能了解全年的阅读量,没有帮助;
C:不同年级的借阅量不相同,不能只根据一个班的借阅量确定全校的借阅量,没有帮助;
D:一个人上周借阅的本数与全校的阅读量无关。
故答案为:A。
了解全校学生的阅读量有多种方法,根据每个选项中给出的条件分析,然后确定能了解全校阅读量的方法即可。
28.C
解:A:100:1的比例尺是放大的比例尺,不合适;
B:1:10表示实际距离缩小了10倍,不合适;
C:1:100表示实际距离缩小了100倍,合适;
D:1:20000表示把实际距离缩小了20000倍,不合适。
故答案为:C。
比例尺表示图上距离与实际距离的比。教室实际的长大约10米,缩小100倍是10厘米,所以1:100的比例尺比较合适。
29.B
解:A:形状变了,体积不变,正确;
B:体积不变,表面积变大,原来说法错误;
C:长方体的长等于底面周长的一半,就是πr,正确;
D:长方体的高等于圆柱的高,正确。
故答案为:B。
按照这种方法拼成近似长方体后,体积不变,表面积比原来增加了左右两个长方形的面;长方体的长就是圆柱的底面周长,宽是圆柱的底面半径,高是圆柱的高。
30.C
解: 将原来的正方体向左翻转一个面后的图形。
故答案为:C。
观察原来图形的右面,刚好在C项中上面,其余两个面也相对应。
31.B
解:在如图中再添一个“□”(□的边长是1cm),新添的正方形有一条边和原图形的边完全重合时,新图形的周长增加2cm。
故答案为:B。
因为只有一条边和原图形的边完全重合,所以周长会减少2条重合的边,因为正方形有4条边,所以周长只增加了2条小正方形的边长。
32.B
解:92×5≈450(千米),所以该服务区的位置最有可能是中点F。
故答案为:B。
用每小时行的路程乘时间求出5小时行驶的路程,然后根据行驶的路程和总路程确定该服务区的位置即可。
33.C
解:可以呈现出算式的计算过程和结果。
故答案为:C。
先把整个图形平均分成5份,其中的3份涂浅色表示;又把涂色部分平均分成3份,给其中的2份涂重色就表示。
34.B
解:6米=60分米,4.8米=48分米
60和48的最大公因数是2×2×3=12,也就是方砖的边长最大是12分米
12分米=120厘米,四个选项中,只有60厘米是120厘米的因数。
故答案为:B。
先用短除法求出赵伟家客厅长、宽的最大公因数是12,也就是12分米=120厘米,观察4个选项中是120的因数的即可。
35.B
解:180÷(1+2+3)×3
=180÷6×3
=30×3
=90(度),这个是直角三角形。
故答案为:B。
这个三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数。
36.B
解:
因为>>,所以x<z<y。
故答案为:B。
两个数相加的和相等,较小的数要加上较大的数。
37.C
解:÷=5(千米/时)。
故答案为:C。
速度=行驶的路程÷用的时间。
38.A
解:在出油率、出勤率、合格率、成活率中,不可能达到100%的是出油率。
故答案为:A。
出勤率、合格率和成活率都有可能达到100%,但不会超过100%;出油率是一定不会达到100%。
39.C
解:如图是一个正方体纸盒的展开图,当还原折成纸盒时,与点1重合的点是点7和11。
故答案为:C。
假设一个面是底面,然后确定前后面,左右面、上下面,然后确定与1重合的点即可。
40.C
解:5÷20=25%,表示甲是乙的25%。
故答案为:C。
甲是第一个因数与5的乘积,乙是第一个因数与20的乘积,乙一定大于甲,用5除以20即可求出甲是乙的百分之几。
41.A
解:第一幅图:图中两条直线,应该表示两种情况,所以应该表示龟兔赛跑;
第二幅图:表示一种元素,且线呈下降趋势,应该是表示司马光砸缸中水的高度不断下降;
第三幅图:表示一种元素,且线呈上升趋势,应该是表示乌鸦喝水中水面的高度不断上升。
故答案为:A。
用折线表示元素的变化情况,两条折线就表示两种元素,折线上升和下降表示的意义是不同的。
42.D
解:A:n<m,所以错误;
B:mn无法和m比较大小,错误;
C:m>1,所以<1,错误;
D:>1,正确。
故答案为:D。
0<n<1,1<m<2,分母大于分子的分数都小于1,分母小于分子的分数都大于1。
43.A
解:a÷4=(米)
故答案为:A。
用这段铁丝的长度除以平均分的段数,用分数表示出每段铁丝的长度即可。
44.C
解:①宽是长的9÷16=,正确;
②宽比长短(16-9)÷16=,错误;
③长是宽的16÷9=,正确;
④长比宽长(16-9)÷9=,正确。
故答案为:C。
把长看作16,宽看作9,用长除以宽即可求出长是宽的几分之几;用宽除以长即可求出宽是长的几分之几;用长与宽的差除以长即可求出宽比长短几分之几;用长与宽的差除以宽即可求出长比宽长几分之几。
45.B
解:1号店:54÷10=5(组)······4(个)
(54-5×3)×48
=39×48
=1872(元);
2号店:54×48×70%
=2592×70%
=1814.4(元)
3号店:54×48=2592(元)
2592÷200=12(组)······192(元)
2592-12×50
=2592-600
=1992(元)
1814.4<1872<1992。
故答案为:B。
1号店总价=(要买的个数-送的个数)×单价;
2号店总价=单价×数量×折扣;
3号店总价=单价×数量-减免的钱数,然后比较大小。
46.A
解:如图所示:
第一类:形如的有2种,
第二类:形如有8种
所以共有:2+8=10(种)
故答案为:A
可以分成两类,第一类,分成两个长方形,第二类,分成两个不规则图形,分别数出各类的数量,相加得到总数。
47.D
解:(300+240)×35=18900(m)
18900÷2400=7(全长)……2100(m).
迎面相遇(7+1)÷2=4(次)
t一定
第1次相遇,共走1全长 (全长),离A地有 全长。
第2次相遇,共走3全长 (全长),离A 地有 全长。
第3次相遇,共走5全长 (全长),离A 地有 全长,
第4次相遇,共走7全长, (全长),离A 地有 全长。
则第4次相遇离A地最近。
故答案为:D。
先用速度和乘时间求出甲、乙所走总路程,然后根据全长求出相遇次数,再根据相遇次数依次求出距A地距离再比较。
48.A;C
把若干个棱长为1厘米的小正方体木块搭成一个图形,从上面和前面看到的都是如图所示那样,搭成这这个图形最多需要9个,最少需要7个这样的小正方体;
最多为
共2×4+1=9(个)
最少为
或或,共2×2+1×3=7(个)。
故答案为:A,C.
把若干个棱长为1厘米的小正方体木块搭成一个图形,从上面和前面看到的都是如图所示那样,它下层有5个小正方体,分成2行,前行3个,后行2个,左对齐,上层4个或2个,若4个,分别在下层左边4个小正方体的上边,若2个,在下层左边4个小正方体的上边,前后不成一行即可,因此,搭成这这个图形最多需要9个,最少需要7个这样的小正方体.
49.A
解:(次)
(次)
则所运次数应大于6 次,小于8 次,满足条件的次数为7次或8次,最多应为8次。
故答案为:A。
先根据已运次数和对应分率求出总次数的范围,再结合问题分析最值。
50.A
解:20%的狗认为自己是猫,20%的猫认为自己是狗,则80%的猫认为自己是猫,而所有动物中,有32%认为自己是猫。
48%:12%=4:1,则狗:猫=4:1
狗:180÷(4-1)×4=240(只)
故答案为:A。
应用“十字交叉法”求出两种动物的数量比,再根据数量差和比例关系列式计算。
同课章节目录
