2024-2025学年小升初数学备考真题分类汇编(广东地区专版)专题5 计算题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(广东地区专版)专题5 计算题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 65.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 07:30:01 | ||
图片预览


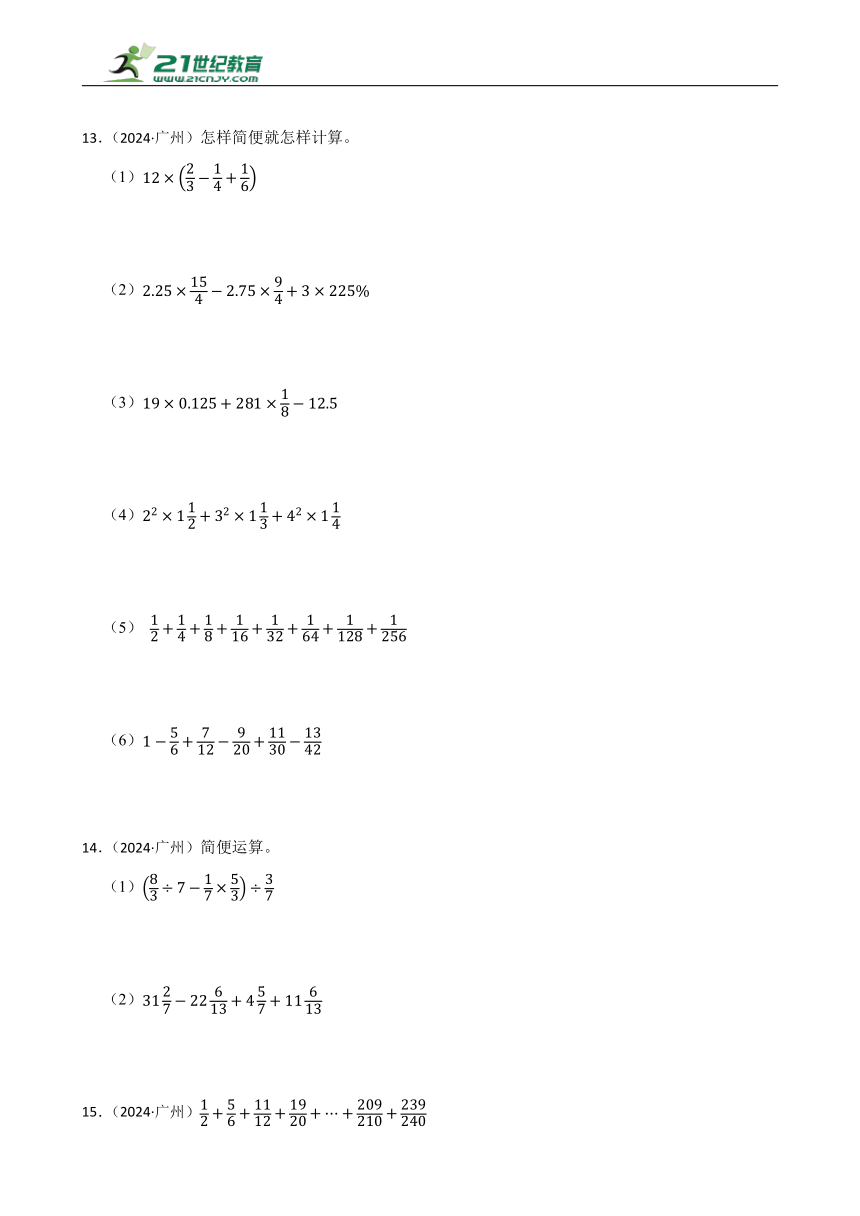
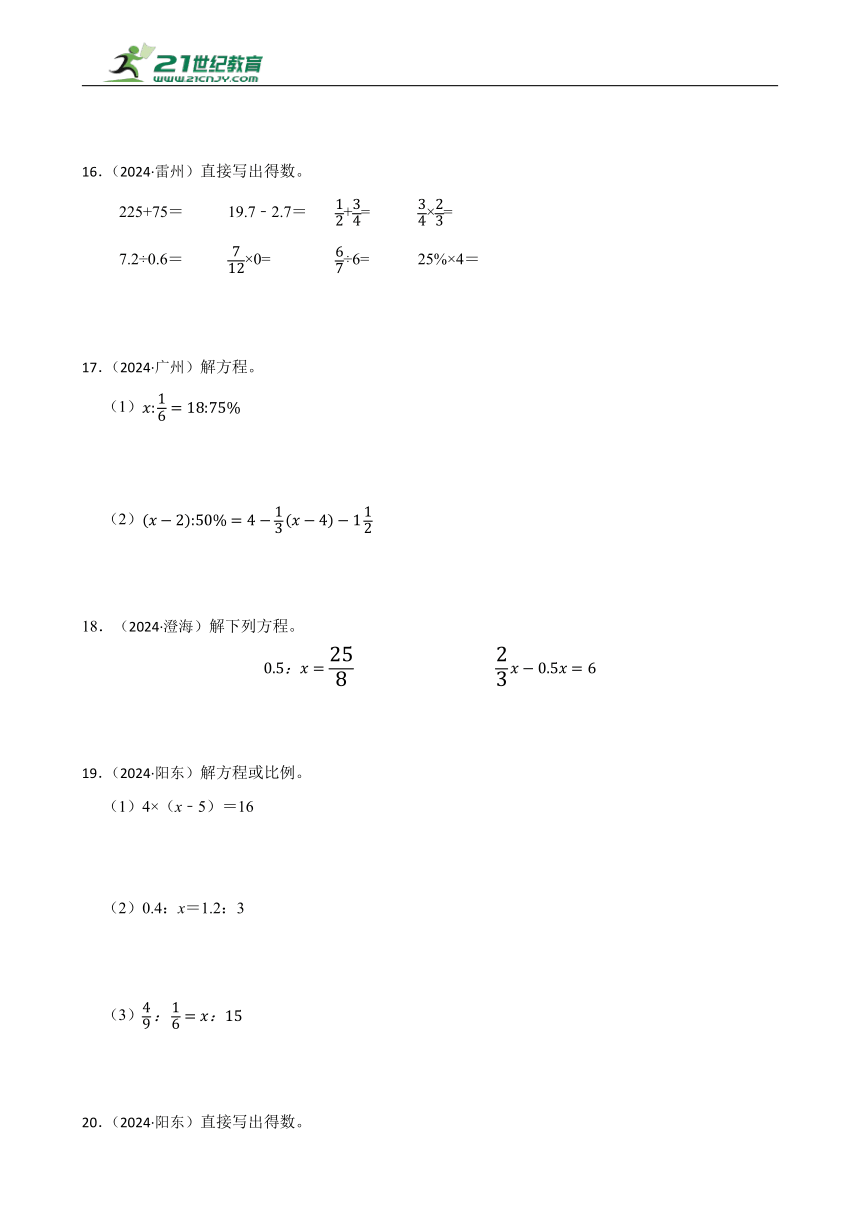
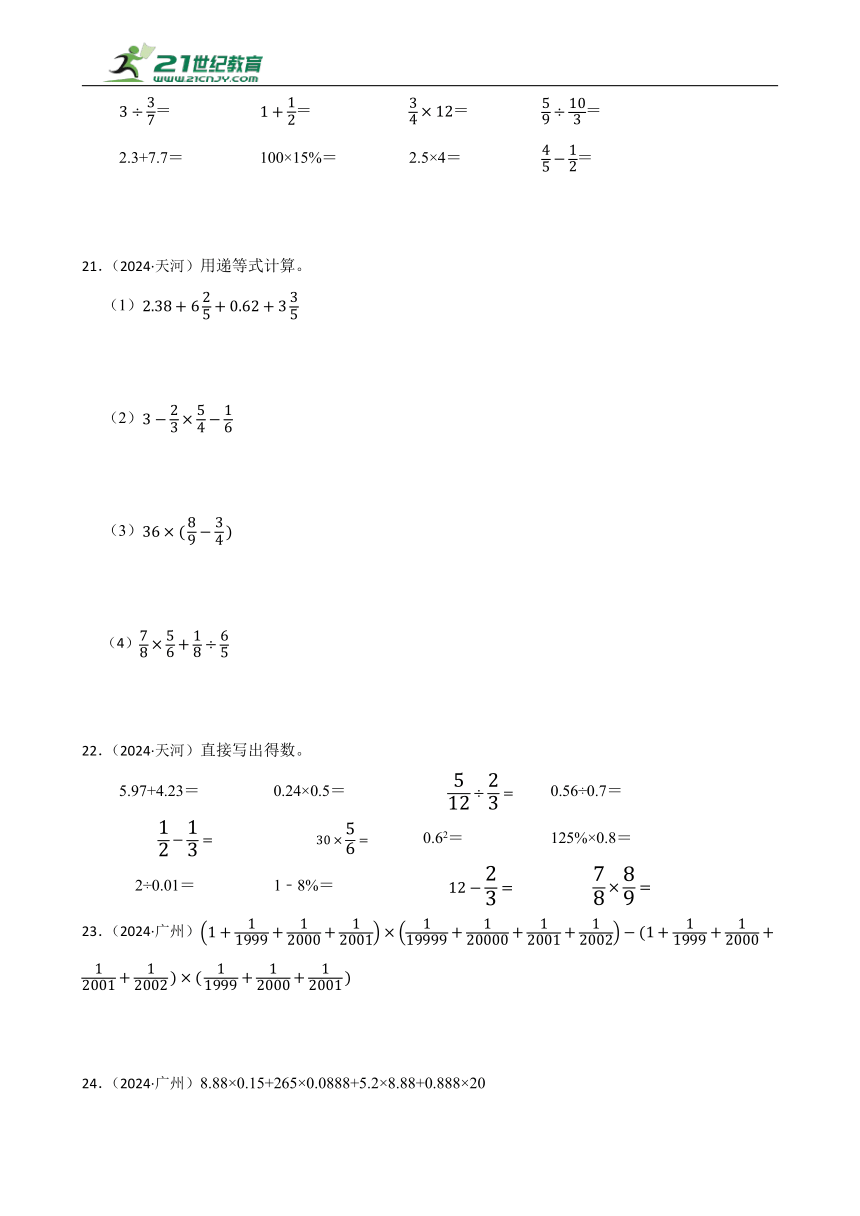
文档简介
专题5 计算题-2023-2024学年
小升初数学备考真题分类汇编(广东地区专版)
试卷说明:
本试卷试题精选自广东省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广东省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、计算题
1.(2024·天河)解方程或比例。
x+x=45 :x=:12
2.(2024·深圳)计算:
3.(2024·广州)
4.(2024·广州)(解方程)
5.(2024·广州)(解方程)
6.(2024·广州)
7.(2024·广州)
8.(2024·广州)
9.(2024·广州)
10.(2024·广州)解下列方程。
(1)
(2)
(3)
11.(2024·广州)脱式计算。
(1)
(2)
(3)
12.(2024·广州)解方程。
(1)4x-1.2×3=2
(2)3x+80%x=4.56
13.(2024·广州)怎样简便就怎样计算。
(1)
(2)
(3)
(4)
(5)
(6)
14.(2024·广州)简便运算。
(1)
(2)
15.(2024·广州)
16.(2024·雷州)直接写出得数。
225+75= 19.7﹣2.7= += ×=
7.2÷0.6= ×0= ÷6= 25%×4=
17.(2024·广州)解方程。
(1)
(2)
(2024·澄海)解下列方程。
19.(2024·阳东)解方程或比例。
(1)4×(x﹣5)=16
(2)0.4:x=1.2:3
(3)
20.(2024·阳东)直接写出得数。
= = = =
2.3+7.7= 100×15%= 2.5×4= =
21.(2024·天河)用递等式计算。
(1)
(2)
(3)
22.(2024·天河)直接写出得数。
5.97+4.23= 0.24×0.5= 0.56÷0.7=
0.62= 125%×0.8=
2÷0.01= 1﹣8%=
23.(2024·广州)
24.(2024·广州)8.88×0.15+265×0.0888+5.2×8.88+0.888×20
25.(2024·广州)
26.(2024·广州)784070+78407.1+7840.72+784.073+78.4074
27.(2024·澄海)计算下面各题。
0.76++1.24+
28.(2024·广州)解方程。
(1)
(2)
(3)
29.(2024·雷州)解方程。
x﹣20%x=40 5x+18=48 :=15:x
30.(2024·雷州)脱式计算,能简算的要简算。
75+450÷18 +×
12×(+-) 0.7+3.9+4.3+6.1
答案解析部分
1.
x+x=45
解:x=45
x=45÷
x=54
:x=:12
解:x=12×
x=
x=÷
x=7
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先计算+=,然后应用等式的性质2,等式两边同时除以。
比例的基本性质:在比例里,两个内项积等于两个外项积。应用比例的基本性质解比例。
2.
将带分数拆分为整数部分与分数部分分别相加,整数部分是等比数列,可直接相加,分数部分通过逐步凑相同分母进行简便运算。
3.解:
=0.1×0.9
=0.09
先将带分数化成假分数,然后再将除法换算成乘法,再对小括号里面的小数进行运算,再对中括号里面的分数进行约分运算,然后再利用乘法交换律,先对2.5×0.04,最后再进行约分即可求解
4.解:
3x=5
根据等式的基本性质:等式两边同时减去2x,再同时减去,最后再同时除以3,即可求解
5.解:
根据等式的基本性质:等式两边同时加上,然后再对方程两边进行通分运算,最后方程两边同时除以,即可求解
6.解:
先对分式进行裂项:,最后再进行运算即可
7.解:设
A+B=1×2+2×3+3×4+…+98×99+99×100
= [(1×2×3-0×1×2)+(2×3×4-1×2×3)+…+(99×100×101-98×99×100)]
B-A=1×2+3×2+5×2+…+99×2=50×100=5000
利用换元法分别用B和A表示原式的分子和分母;分别计算出B-A和B+A的值,则分子B=(A+B)+(B-A),分母A=(A+B)-(B-A),代入原式求解。
8.解:
根据通项可以对原式中的分数进行拆分;将分数分成两组,第一组通过裂项可以凑出能够正负相消的分数,进行简算;第二组首先提取公因式,再进行裂项和正负抵消;最后按照四则运算顺序进行计算即可。
9.解:
首先对分数进行简化,从每个分数中拆出一个“1”;对分母进行因式分解,利用分数的裂项将分数化成可以相互抵消的加减混合算式,将可以抵消的分数消去,进行加减混合运算即可。
10.(1)4(x-3)=2x
解:4x-12=2x
2x=12
x=6
(2)4x+2(7-x)=32
解:4x+14-2x=32
2x=18
x=9
(3)解:
(1)先去括号,然后再将未知项移到左边,常数项移到右边,然后再进行合并同类项,最后再将系数化为1即可
(2)先去括号,然后再将未知项移到左边,常数项移到右边,然后再进行合并同类项,最后再将系数化为1即可
(3)先将比例方程化成方程:,然后再对方程右边进行约分运算,最后再将系数化为1即可
11.(1)解:
(2)解:
=2
(3)解:
(1)先去括号,再根据加法交换律和加法结合律简便计算。
(2)原式利用除法法则变形,再逆用乘法分配律计算即可得到结果.
(3)先算小括号里面的加法,再算乘法,接着算除法,最后算减法。
12.(1)4x-1.2×3=2
解:4x-3.6=2
4x=5.6
x=1.4
(2)3x+80%x=4.56
解:3.8x=4.56
x=4.56÷3.8
x=1.2
方程求解,主要依据等式的性质,通过移项、合并同类项等操作,将方程化简为ax=b(a、b为常数,a≠0)的形式,进而求出x的值。
13.(1)解:
(2)解:%
=9
(3)解:
=19×0.125+281×0.125-100×0.125
=0.125×(19+281-100)
=0.125×200
=25
(4)解:
=6+12+20
=18+20
=38
(5)解:
(6)解:
(1)根据乘法分配律进行简算。
(2)根据分数、百分数和小数的互化以及乘法分配律的逆运算,进行计算即可.
(3)原式变形后,利用乘法分配律计算即可求出值.
(4)把带分数化成假分数,先算乘方,再算乘法,最后算加法,由此顺序计算即可。
(5)先把原式化为++++++++-,即原式=1-,据此解答即可。
(6)通过观察,把每个分数拆成两个分数相加的形式,然后通过加减相互抵消,求得结果。
14.(1)解:
(2)解:
=36-11
=25
(1)先将除法换算成乘法,然后再进行约分,运算即可
(2)先对分式进行重组:,最后再进行运算即可
15.解:
根据题意,将分数拆分成两个分数相减的形式,再抵消中间相同的分数,即可简便计算
16.
225+75=300 19.7﹣2.7=17 += ×=
7.2÷0.6=12 ×0=0 ÷6= 25%×4=1
计算小数减法和除法时要注意小数点的位置;异分母分数相加减,先通分再按照同分母分数加减法的计算方法计算;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法计算;含有百分数的把百分数化成小数或分数再计算。
17.(1)x: =18:75%
解:
0.75x=3
x=3÷0.75
x=4
(2)解:
(1)先将比例方程化成:,然后再将百分数化成小数,方程右边进行约分,最后再将系数化为1即可求解
(2)先将比例方程化为:,然后再对方程的右边进行合并运算,最后再将系数化为1即可求解
18.解:0.5:x=
25x=0.5×8
25x=4
x=4÷25
x=
x-0.5x=6
解:x=6
x=6÷
x=36
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质解比例;
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先计算-0.5=,然后应用等式的性质2,等式两边同时除以 ,计算出结果。
19.(1) 4×(x﹣5)=16
解:4×(x-5)÷4=16÷4
x-5+5=4+5
x=9
(2) 0.4:x=1.2:3
解:1.2x=0.4×3
x=1
(3)
解:x=
x=
x=40
等式的性质1:等式两边同时加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边同时乘一个数,或同时除以一个不是0的数,两边仍然相等。
(1)把方程两边同时除以4,再同时加上5即可求出x的值;
(2)、(3)比例的基本性质:在比例里,两个内项的积等于两个内项的积。解比例时根据比例的基本性质把比例写成两个內项积等于两个外项积的形式,然后根据等式的性质求出未知数的值。
20.
=7 = =9 =
2.3+7.7=10 100×15%=15 2.5×4=10 =
计算小数加法时把小数点对齐;异分母分数相加减,先通分再按照同分母分数加减法的计算方法计算;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法计算;含有百分数的把百分数化成小数或分数再计算。
21.(1)解:
=(2.38+0.62)+(+)
=3+10
=13
(2)解:
=3-(+)
=3-1
=2
(3)解:36×(-)
=36×-36×
=32-27
=5
(4)解:
=(+)×
=1×
=
(1)应用加法交换律、加法结合律,把(2.38+0.62)与(+)结合在一起先计算;
(2)一个数连续减去两个数,等于这数减去后面两个数的和;
(3)应用乘法分配律,括号外面的数分别与括号里面的数相乘,再把所得的积相减;
(4)应用乘法分配律,先计算(+)=1,然后再乘。
22.
5.97+4.23=10.2 0.24×0.5=0.12 0.56÷0.7=0.8
25 0.62=0.36 125%×0.8=1
2÷0.01=200 1-8%=0.92
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
23.解:设 则B-A
=(1+A)×B-(1+B)×A
=B+AB-A-AB
=B-A
设则B-A ,代入原式,即可求解
24.解:8.88×0.15+265×0.0888+5.2×8.88+0.888×20
=8.88×0.15+2.65×8.88+5.2×8.88+8.88×2
=8.88×(0.15+2.65+5.2+2)
=8.88×10
=88.8
先对式子进行变形:8.88×0.15+2.65×8.88+5.2×8.88+8.88×2,然后再利用乘法分配律,对式子进行简便运算即可
25.解:
将1999拆分成:(1998+1),然后再利用乘法分配律,对式子进行约分运算即可
26.解:784070+78407.1+7840.72+784.073+78.4074
=784070+78407+0.1+7840.7+0.02 +784.07+0.003+78.407+0.0004
=784070×(1+0.1+0.01+0.001+0.0001)+(0.1+0.02+0.003+0.0004)
=784070×1.1111+0.1234
=871180.177+0.1234
=871180.3004
将式子拆分成成:784070+78407+0.1+7840.7+0.02 +784.07+0.003+78.407+0.0004,然后再将对式子进一步进行变形:784070×(1+0.1+0.01+0.001+0.0001)+(0.1+0.02+0.003+0.0004),最后再进行运算即可
27.解:0.76++1.24+
=(0.76+1.24)+(+)
=2+1
=3
÷8+×
=(+)×
=1×
=
15+9÷×
=15+16
=31
48÷[(7.5-5.1)×]
=48÷[2.4×]
=48÷1.2
=40
应用加法交换律、加法结合律,变成 (0.76+1.24)+(+) ,先算括号里面的,再算括号外面的;
应用乘法分配律,先计算(+)=1,然后再乘;
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母,先算第二级运算,再算第一级运算;
分数、小数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
28.(1)1.5x+1.8=3x
解:3x-1.5x=1.8
1.5x=1.8
(2)解:
x=18
(3)6x-12.8×3=0.06
解:6x-38.4=0.06
6x=38.46
x=6.41
(1) 1.5x移到右边变为3x 1.5x,左边剩下1.8。得到1.5x=1.8。两边同时除以1.5, 化简后得出x=。
(2) x是除数,所以x就等于被除数15除以商 。
(3) 先算出12.8×3的结果,把原方程化简。根据等式性质,在等式两边加上算出的结果,让方程一边只含6x。最后等式两边同时除以6,求出x=6.41。
29. x﹣20%x=40
解:0.8x÷0.8=40÷0.8
x=50
5x+18=48
解:5x+18-18=48-18
5x÷5=30÷5
x=6
:=15:x
解:x=15×
x=÷
x=5
等式的性质1:等式两边同时加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边同时乘一个数,或同时除以一个不是0的数,两边仍然相等。比例的基本性质:在比例里,两个内项的积等于两个内项的积。
(1)先计算出方程左边的部分,然后把方程两边同时除以0.8即可;
(2)根据比例的基本性质把比例写成两个內项积等于两个外项积的形式,然后根据等式的性质求出未知数的值。
30.解:75+450÷18
=75+25
=100
+×
=+
=
12×(+-)
=12×+12×-12×
=2+3-4
=1
0.7+3.9+4.3+6.1
=(0.7+4.3)+(3.9+6.1)
=5+10
=15
第一题:先算除法,再算加法;
第二题:先算乘法,再算加法;
第三题:运用乘法分配律简便计算;
第四题:运用加法交换律和结合律,把得数是整数的两个数相加。
小升初数学备考真题分类汇编(广东地区专版)
试卷说明:
本试卷试题精选自广东省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广东省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、计算题
1.(2024·天河)解方程或比例。
x+x=45 :x=:12
2.(2024·深圳)计算:
3.(2024·广州)
4.(2024·广州)(解方程)
5.(2024·广州)(解方程)
6.(2024·广州)
7.(2024·广州)
8.(2024·广州)
9.(2024·广州)
10.(2024·广州)解下列方程。
(1)
(2)
(3)
11.(2024·广州)脱式计算。
(1)
(2)
(3)
12.(2024·广州)解方程。
(1)4x-1.2×3=2
(2)3x+80%x=4.56
13.(2024·广州)怎样简便就怎样计算。
(1)
(2)
(3)
(4)
(5)
(6)
14.(2024·广州)简便运算。
(1)
(2)
15.(2024·广州)
16.(2024·雷州)直接写出得数。
225+75= 19.7﹣2.7= += ×=
7.2÷0.6= ×0= ÷6= 25%×4=
17.(2024·广州)解方程。
(1)
(2)
(2024·澄海)解下列方程。
19.(2024·阳东)解方程或比例。
(1)4×(x﹣5)=16
(2)0.4:x=1.2:3
(3)
20.(2024·阳东)直接写出得数。
= = = =
2.3+7.7= 100×15%= 2.5×4= =
21.(2024·天河)用递等式计算。
(1)
(2)
(3)
22.(2024·天河)直接写出得数。
5.97+4.23= 0.24×0.5= 0.56÷0.7=
0.62= 125%×0.8=
2÷0.01= 1﹣8%=
23.(2024·广州)
24.(2024·广州)8.88×0.15+265×0.0888+5.2×8.88+0.888×20
25.(2024·广州)
26.(2024·广州)784070+78407.1+7840.72+784.073+78.4074
27.(2024·澄海)计算下面各题。
0.76++1.24+
28.(2024·广州)解方程。
(1)
(2)
(3)
29.(2024·雷州)解方程。
x﹣20%x=40 5x+18=48 :=15:x
30.(2024·雷州)脱式计算,能简算的要简算。
75+450÷18 +×
12×(+-) 0.7+3.9+4.3+6.1
答案解析部分
1.
x+x=45
解:x=45
x=45÷
x=54
:x=:12
解:x=12×
x=
x=÷
x=7
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先计算+=,然后应用等式的性质2,等式两边同时除以。
比例的基本性质:在比例里,两个内项积等于两个外项积。应用比例的基本性质解比例。
2.
将带分数拆分为整数部分与分数部分分别相加,整数部分是等比数列,可直接相加,分数部分通过逐步凑相同分母进行简便运算。
3.解:
=0.1×0.9
=0.09
先将带分数化成假分数,然后再将除法换算成乘法,再对小括号里面的小数进行运算,再对中括号里面的分数进行约分运算,然后再利用乘法交换律,先对2.5×0.04,最后再进行约分即可求解
4.解:
3x=5
根据等式的基本性质:等式两边同时减去2x,再同时减去,最后再同时除以3,即可求解
5.解:
根据等式的基本性质:等式两边同时加上,然后再对方程两边进行通分运算,最后方程两边同时除以,即可求解
6.解:
先对分式进行裂项:,最后再进行运算即可
7.解:设
A+B=1×2+2×3+3×4+…+98×99+99×100
= [(1×2×3-0×1×2)+(2×3×4-1×2×3)+…+(99×100×101-98×99×100)]
B-A=1×2+3×2+5×2+…+99×2=50×100=5000
利用换元法分别用B和A表示原式的分子和分母;分别计算出B-A和B+A的值,则分子B=(A+B)+(B-A),分母A=(A+B)-(B-A),代入原式求解。
8.解:
根据通项可以对原式中的分数进行拆分;将分数分成两组,第一组通过裂项可以凑出能够正负相消的分数,进行简算;第二组首先提取公因式,再进行裂项和正负抵消;最后按照四则运算顺序进行计算即可。
9.解:
首先对分数进行简化,从每个分数中拆出一个“1”;对分母进行因式分解,利用分数的裂项将分数化成可以相互抵消的加减混合算式,将可以抵消的分数消去,进行加减混合运算即可。
10.(1)4(x-3)=2x
解:4x-12=2x
2x=12
x=6
(2)4x+2(7-x)=32
解:4x+14-2x=32
2x=18
x=9
(3)解:
(1)先去括号,然后再将未知项移到左边,常数项移到右边,然后再进行合并同类项,最后再将系数化为1即可
(2)先去括号,然后再将未知项移到左边,常数项移到右边,然后再进行合并同类项,最后再将系数化为1即可
(3)先将比例方程化成方程:,然后再对方程右边进行约分运算,最后再将系数化为1即可
11.(1)解:
(2)解:
=2
(3)解:
(1)先去括号,再根据加法交换律和加法结合律简便计算。
(2)原式利用除法法则变形,再逆用乘法分配律计算即可得到结果.
(3)先算小括号里面的加法,再算乘法,接着算除法,最后算减法。
12.(1)4x-1.2×3=2
解:4x-3.6=2
4x=5.6
x=1.4
(2)3x+80%x=4.56
解:3.8x=4.56
x=4.56÷3.8
x=1.2
方程求解,主要依据等式的性质,通过移项、合并同类项等操作,将方程化简为ax=b(a、b为常数,a≠0)的形式,进而求出x的值。
13.(1)解:
(2)解:%
=9
(3)解:
=19×0.125+281×0.125-100×0.125
=0.125×(19+281-100)
=0.125×200
=25
(4)解:
=6+12+20
=18+20
=38
(5)解:
(6)解:
(1)根据乘法分配律进行简算。
(2)根据分数、百分数和小数的互化以及乘法分配律的逆运算,进行计算即可.
(3)原式变形后,利用乘法分配律计算即可求出值.
(4)把带分数化成假分数,先算乘方,再算乘法,最后算加法,由此顺序计算即可。
(5)先把原式化为++++++++-,即原式=1-,据此解答即可。
(6)通过观察,把每个分数拆成两个分数相加的形式,然后通过加减相互抵消,求得结果。
14.(1)解:
(2)解:
=36-11
=25
(1)先将除法换算成乘法,然后再进行约分,运算即可
(2)先对分式进行重组:,最后再进行运算即可
15.解:
根据题意,将分数拆分成两个分数相减的形式,再抵消中间相同的分数,即可简便计算
16.
225+75=300 19.7﹣2.7=17 += ×=
7.2÷0.6=12 ×0=0 ÷6= 25%×4=1
计算小数减法和除法时要注意小数点的位置;异分母分数相加减,先通分再按照同分母分数加减法的计算方法计算;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法计算;含有百分数的把百分数化成小数或分数再计算。
17.(1)x: =18:75%
解:
0.75x=3
x=3÷0.75
x=4
(2)解:
(1)先将比例方程化成:,然后再将百分数化成小数,方程右边进行约分,最后再将系数化为1即可求解
(2)先将比例方程化为:,然后再对方程的右边进行合并运算,最后再将系数化为1即可求解
18.解:0.5:x=
25x=0.5×8
25x=4
x=4÷25
x=
x-0.5x=6
解:x=6
x=6÷
x=36
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质解比例;
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先计算-0.5=,然后应用等式的性质2,等式两边同时除以 ,计算出结果。
19.(1) 4×(x﹣5)=16
解:4×(x-5)÷4=16÷4
x-5+5=4+5
x=9
(2) 0.4:x=1.2:3
解:1.2x=0.4×3
x=1
(3)
解:x=
x=
x=40
等式的性质1:等式两边同时加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边同时乘一个数,或同时除以一个不是0的数,两边仍然相等。
(1)把方程两边同时除以4,再同时加上5即可求出x的值;
(2)、(3)比例的基本性质:在比例里,两个内项的积等于两个内项的积。解比例时根据比例的基本性质把比例写成两个內项积等于两个外项积的形式,然后根据等式的性质求出未知数的值。
20.
=7 = =9 =
2.3+7.7=10 100×15%=15 2.5×4=10 =
计算小数加法时把小数点对齐;异分母分数相加减,先通分再按照同分母分数加减法的计算方法计算;计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法计算;含有百分数的把百分数化成小数或分数再计算。
21.(1)解:
=(2.38+0.62)+(+)
=3+10
=13
(2)解:
=3-(+)
=3-1
=2
(3)解:36×(-)
=36×-36×
=32-27
=5
(4)解:
=(+)×
=1×
=
(1)应用加法交换律、加法结合律,把(2.38+0.62)与(+)结合在一起先计算;
(2)一个数连续减去两个数,等于这数减去后面两个数的和;
(3)应用乘法分配律,括号外面的数分别与括号里面的数相乘,再把所得的积相减;
(4)应用乘法分配律,先计算(+)=1,然后再乘。
22.
5.97+4.23=10.2 0.24×0.5=0.12 0.56÷0.7=0.8
25 0.62=0.36 125%×0.8=1
2÷0.01=200 1-8%=0.92
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
23.解:设 则B-A
=(1+A)×B-(1+B)×A
=B+AB-A-AB
=B-A
设则B-A ,代入原式,即可求解
24.解:8.88×0.15+265×0.0888+5.2×8.88+0.888×20
=8.88×0.15+2.65×8.88+5.2×8.88+8.88×2
=8.88×(0.15+2.65+5.2+2)
=8.88×10
=88.8
先对式子进行变形:8.88×0.15+2.65×8.88+5.2×8.88+8.88×2,然后再利用乘法分配律,对式子进行简便运算即可
25.解:
将1999拆分成:(1998+1),然后再利用乘法分配律,对式子进行约分运算即可
26.解:784070+78407.1+7840.72+784.073+78.4074
=784070+78407+0.1+7840.7+0.02 +784.07+0.003+78.407+0.0004
=784070×(1+0.1+0.01+0.001+0.0001)+(0.1+0.02+0.003+0.0004)
=784070×1.1111+0.1234
=871180.177+0.1234
=871180.3004
将式子拆分成成:784070+78407+0.1+7840.7+0.02 +784.07+0.003+78.407+0.0004,然后再将对式子进一步进行变形:784070×(1+0.1+0.01+0.001+0.0001)+(0.1+0.02+0.003+0.0004),最后再进行运算即可
27.解:0.76++1.24+
=(0.76+1.24)+(+)
=2+1
=3
÷8+×
=(+)×
=1×
=
15+9÷×
=15+16
=31
48÷[(7.5-5.1)×]
=48÷[2.4×]
=48÷1.2
=40
应用加法交换律、加法结合律,变成 (0.76+1.24)+(+) ,先算括号里面的,再算括号外面的;
应用乘法分配律,先计算(+)=1,然后再乘;
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母,先算第二级运算,再算第一级运算;
分数、小数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算。
28.(1)1.5x+1.8=3x
解:3x-1.5x=1.8
1.5x=1.8
(2)解:
x=18
(3)6x-12.8×3=0.06
解:6x-38.4=0.06
6x=38.46
x=6.41
(1) 1.5x移到右边变为3x 1.5x,左边剩下1.8。得到1.5x=1.8。两边同时除以1.5, 化简后得出x=。
(2) x是除数,所以x就等于被除数15除以商 。
(3) 先算出12.8×3的结果,把原方程化简。根据等式性质,在等式两边加上算出的结果,让方程一边只含6x。最后等式两边同时除以6,求出x=6.41。
29. x﹣20%x=40
解:0.8x÷0.8=40÷0.8
x=50
5x+18=48
解:5x+18-18=48-18
5x÷5=30÷5
x=6
:=15:x
解:x=15×
x=÷
x=5
等式的性质1:等式两边同时加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边同时乘一个数,或同时除以一个不是0的数,两边仍然相等。比例的基本性质:在比例里,两个内项的积等于两个内项的积。
(1)先计算出方程左边的部分,然后把方程两边同时除以0.8即可;
(2)根据比例的基本性质把比例写成两个內项积等于两个外项积的形式,然后根据等式的性质求出未知数的值。
30.解:75+450÷18
=75+25
=100
+×
=+
=
12×(+-)
=12×+12×-12×
=2+3-4
=1
0.7+3.9+4.3+6.1
=(0.7+4.3)+(3.9+6.1)
=5+10
=15
第一题:先算除法,再算加法;
第二题:先算乘法,再算加法;
第三题:运用乘法分配律简便计算;
第四题:运用加法交换律和结合律,把得数是整数的两个数相加。
同课章节目录
