2024-2025学年小升初数学备考真题分类汇编(广西地区专版)专题4 解决问题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(广西地区专版)专题4 解决问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 650.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
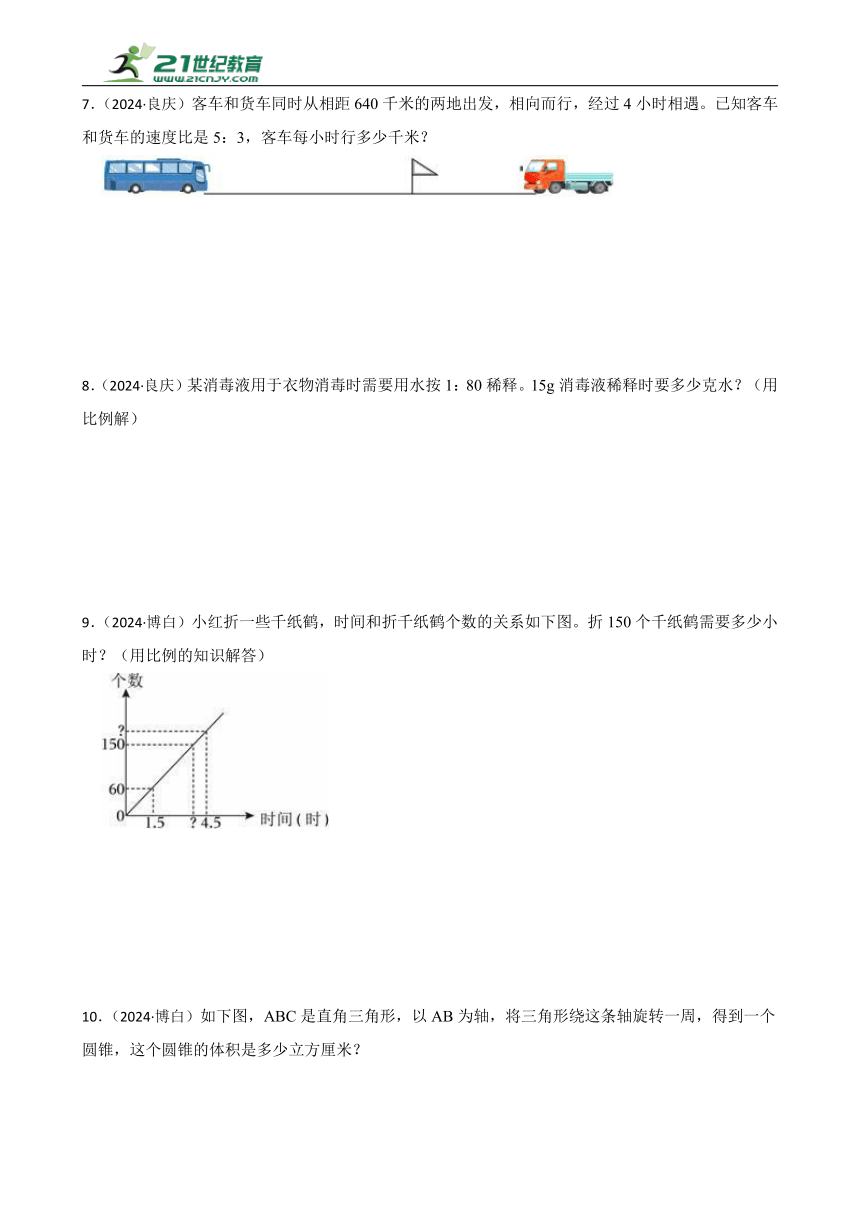
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览



文档简介
专题4 解决问题-2023-2024学年
小升初数学备考真题分类汇编(广西地区专版)
试卷说明:
本试卷试题精选自广西省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广西省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、解决问题
1.(2024·南宁)欢欢一家到餐馆吃饭。点完菜后服务员把一个沙漏摆到桌上,并且说“给您计个时,沙漏漏完前您点的菜都会上桌”。
欢欢发现这是一个上下均为圆锥的沙漏(如下图),两个圆锥的底面直径均是10厘米,高均是6厘米。沙漏上面的圆锥中装满沙子,如果每分钟漏掉10立方厘米的沙子,那么按服务员的承诺最迟多少分钟后欢欢﹣家点的菜会上桌?(得数保留整数)
2.(2024·良庆)工人要在一个圆柱形贮水池的侧面和底面抹一层水泥,抹水泥的面积有多少平方米?
3.(2024·博白)某实验小学六⑴班学生在开学体能测试中达标率为85%,经过一个学期的训练,在期末体能测试中达标的人数增加了4人,达标率上升到95%。六⑴班期末体能测试中达标人数是多少人?
4.(2024·港南)为了打造“全国文明城市”,某市计划在一条道路两旁种紫荆树和玉兰树,紫荆树和玉兰树的棵数比是3:2。已知种了600棵紫荆树,需要种多少棵玉兰树?
5.(2024·南宁)最是书香能宜人,今年的4月23日,是第29个“世界读书日”。学校为同学们准备了丰盛的读书日“大餐”。赵丽读了一本学校推荐的书,如果平均每天读25页,那么8天可以读完;如果赵丽想10天读完,那么平均每天读多少页?(用比例解)
6.(2024·良庆)把一块长方体铁块熔铸成一个底面半径为4dm的圆柱形铁块。这个圆柱形铁块的高是多少?
7.(2024·良庆)客车和货车同时从相距640千米的两地出发,相向而行,经过4小时相遇。已知客车和货车的速度比是5:3,客车每小时行多少千米?
8.(2024·良庆)某消毒液用于衣物消毒时需要用水按1:80稀释。15g消毒液稀释时要多少克水?(用比例解)
9.(2024·博白)小红折一些千纸鹤,时间和折千纸鹤个数的关系如下图。折150个千纸鹤需要多少小时?(用比例的知识解答)
10.(2024·博白)如下图,ABC是直角三角形,以AB为轴,将三角形绕这条轴旋转一周,得到一个圆锥,这个圆锥的体积是多少立方厘米?
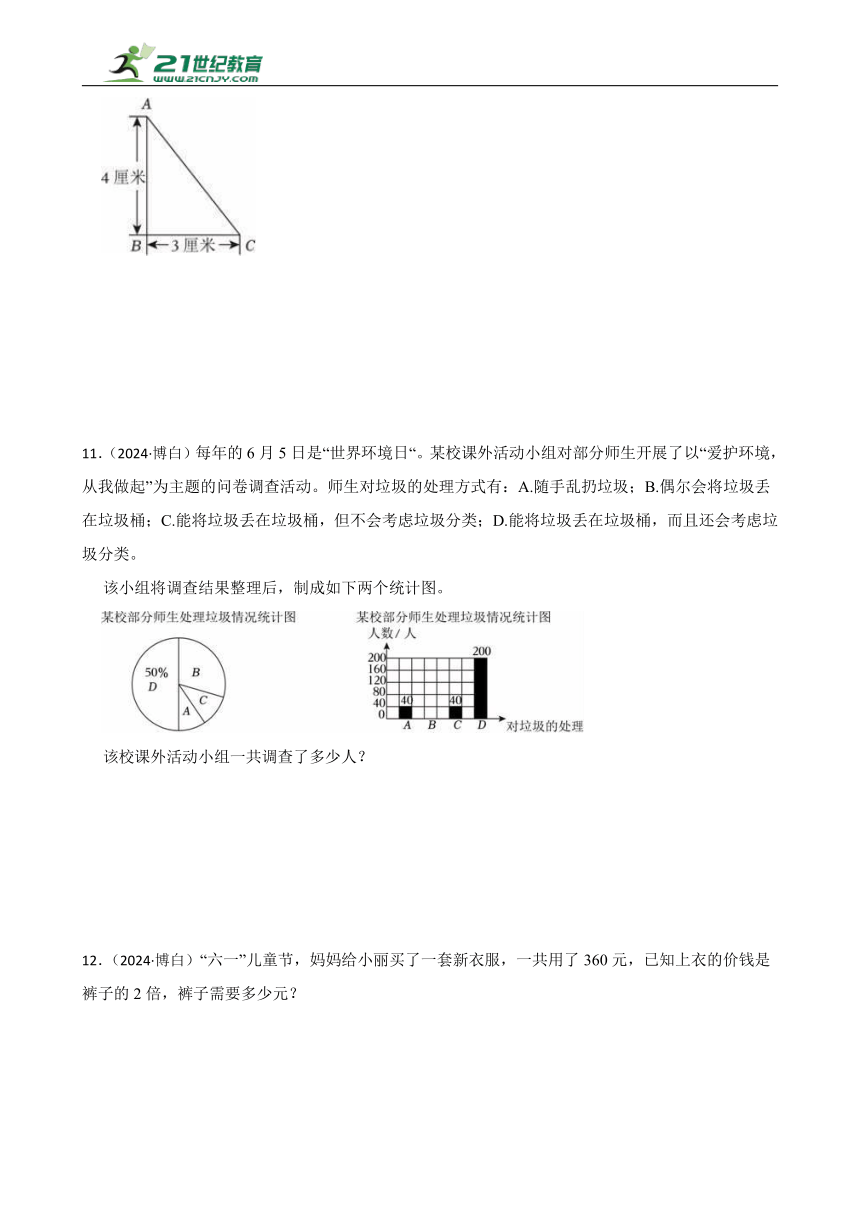
11.(2024·博白)每年的6月5日是“世界环境日“。某校课外活动小组对部分师生开展了以“爱护环境,从我做起”为主题的问卷调查活动。师生对垃圾的处理方式有:A.随手乱扔垃圾;B.偶尔会将垃圾丢在垃圾桶;C.能将垃圾丢在垃圾桶,但不会考虑垃圾分类;D.能将垃圾丢在垃圾桶,而且还会考虑垃圾分类。
该小组将调查结果整理后,制成如下两个统计图。
该校课外活动小组一共调查了多少人?
12.(2024·博白)“六一”儿童节,妈妈给小丽买了一套新衣服,一共用了360元,已知上衣的价钱是裤子的2倍,裤子需要多少元?
13.(2024·港南)某旅行社五一期间推出“北帝山景区一日游”两种购票方案。如果4位大人带6名小孩,怎样购票划算?
方案一: 成人票价160元/人 儿童票价90元/人 方案二: 团体10人以上(包括10人)票价120元/人
14.(2024·港南)蒙古包也称“毡包”,是蒙古族传统民居,如图中的蒙古包是由一个圆柱体和一个圆锥体组成的(单位:米)。这个蒙古包占地多少?内部的空间约是多少?
15.(2024·港南)如下是一张银行定期储蓄存单相关信息,请你帮李军算算到期后他可从银行中提取本金和利息一共多少元?
户名:李军 存期:两年年利率:2.17% 存入日期:2022年7月4日 存入金额:陆仟元整 到期日期:2024年7月4日
16.(2023·南宁)一项工程,甲工程队先做4天,完成了工程的20%,又共做了6天才完成全部工程。如果这项工程甲先做15天,剩下的由乙单独完成,乙还需要多少天?
17.(2023·南宁)一个工厂有三个车间,第一车间与第二车间的人数比是5:3,第三车间的人数占全厂职工人数的,已知第一车间比第二车间多300人,这个工厂一共有多少人?
18.(2023·南宁)一个圆锥形地沙堆,底面周长是12.56米,高6米,已知每立方米的沙子重2吨,如果用一辆载重量为5吨地汽车去运,多少次可以远完?(π取3.14)
19.(2023·南宁)百货大楼搞促销活动,甲品牌鞋满200元减100元,乙品牌鞋“折上折”,就是先打六折,在此基础上再打九折。如果两个品牌都有一双标价260元的鞋,哪个品牌的更便宜?
20.(2023·南宁)饲养场共养480只鸡。母鸡只数比公鸡只数的1.5倍还多30只,公鸡、母鸡各养了多少只?
21.(2023·灵山)小明准备用如图所示的长方形纸板做一个长方体无盖纸盒。
(1)如果纸盒的高都是整厘米数,可以设计几种不同的纸盒?
(2)在你找到的不同设计方案中,纸盒的最大容积是多少立方厘米?(纸板的厚度忽略不计)
22.(2023·灵山)建筑工地运来三堆石子,第二堆比第一堆的多7吨,第三堆比第一堆的少7吨。如果第二、三两堆石子质量的和比第一堆多12吨,三堆石子各多少吨?
23.(2023·武鸣)在一幅比例尺是1:2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5厘米.在另一幅比例尺是1:15000000的地图上,这条公路的图上距离是多少?
24.(2023·武鸣)修建一个圆柱形的沼气池。底面直径是4m,深3m。在池的侧面与下底面抹上水泥。抹水泥部分的面积是多少平方米?
25.(2023·青秀)欢欢一家到餐馆吃饭。点完菜后服务员把一个沙漏摆到桌上,并且说“给您计个时,沙漏漏完前您点的菜都会上桌”。
欢欢发现这是一个上下均为圆锥的沙漏(如图),两个圆锥的底面直径均是10厘米,高均是6厘米。沙漏上面的圆锥中装满沙子,如果每分钟漏掉10立方厘米的沙子,那么按服务员的承诺最迟多少分钟后欢欢一家点的菜会上桌?(得数保留整数)
26.(2023·青秀)“和谐号”动车组的速度可达300km/h,小汽车的速度是“和谐号”速度的 ,是一架喷气式飞机的 。小汽车和喷气式飞机的速度分别是多少?
27.(2023·贺州)贺州园博园位于贺江南岸,莲塘镇与鹅塘镇交界处,以“山水贺寿,诗意乡愁”为主题,意境极富诗意,吸引了大批游客前来观光。“五一”节,小军一家驾车从富川县城到贺州园博园参观。如图表示的是开车从富川县城到贺州园博园行驶的路程与耗油量之间的关系。
(1)行驶的路程和耗油量成什么比例关系?请说明理由。 。
(2)从富川县城到贺州园博园的路程有64km,汽车耗油 L。
(3)小军一家游览完贺州园博园后,想驾车去距离32km的姑婆山。此时油箱里大约剩下3L汽油,算一算,他们需要加油吗?
28.(2023·贺州)绿色生态是我们贺州最亮丽的底色,而绿色出行是保护贺州“绿色环保生态文明”最有效的方式之一。为此,我们开展“绿色低碳文明出行”调查访问活动,如图是调查某公司职员的出行方式后,制成的两幅统计图。
(1)本次“绿色低碳文明出行”调查活动一共调查访问了 人。
(2)请你将统计图补充完整。
(3)骑自行车出行的有 人,自驾车出行的占 %。
(4)文明健康新风尚,绿色环保我先行,观察如图的数据,你打算如何行动?
29.(2023·贺州)为进一步提升寿城群众幸福感,寿城贺州在加快城市公园建设步伐,目前在建的南堤公园广场面积大约0.4公顷,如果用长80cm,宽40cm的长方形地砖铺地,至少需要用多少块这样的地砖?
30.(2023·贺州)如图中每个小方格的边长代表1厘米。
(1)在方格纸上找出点A(4,6)、B(2,3),C(4,3)并将三点连接起来形成三角形①;
(2)画出把三角形①绕C点顺时针旋转90°后得到的图②;
(3)画出把图②按2:1放大后得到的图③;
(4)根据比例尺计算出图③的实际面积是多少公顷。
答案解析部分
1.解:×3.14×(10÷2)2×6÷10
=×3.14×25×6÷10
=157÷10
≈16(分钟)
答:按服务员的承诺最迟16分钟后欢欢一家点的菜会上桌。
按服务员的承诺欢欢一家点的菜会上桌最迟需要的时间=×π×半径2×高÷平均每分钟漏掉沙子的体积。
2.解:3.14×4×2×5+3.14×42
=3.14×40+3.14×16
=3.14×(40+16)
=3.14×56
=175.84(平方米)
答:抹水泥的面积有175.84平方米。
抹水泥的面积=π×半径×2×高+π×半径2。
3.解:4÷(95%﹣85%)×95%
=4÷0.1×0.95
=40×0.95
=38(人)
答:六(1)班期末体能测试中达标人数是38人。
根据分数除法的意义,用增加的4人除以增加的百分率即可求出总人数,用总人数乘95%即可求出达标的人数。
4.解:设需要种x棵玉兰树。
600:x=3:2
3x=1200
x=400
答:要种400棵玉兰树。
设需要种x棵玉兰树。 依据种紫荆树的棵数:需要种玉兰树的棵数=3:2,列比例,解比例。
5.解:设平均每天要读x页。
10x=25×8
10x=200
10x÷10=200÷10
x=20
答:平均每天读20页。
设平均每天要读x页。依据赵丽想读完的天数×平均每天要读的页数=计划平均每天读的页数×计划读的天数,列比例,解比例。
6.解:18.84×8×6÷(3.14×42)
=904.32÷50.24
=18(分米)
答:这个圆柱铁块的高是18分米。
这个圆柱铁块的高=圆柱的体积÷圆柱的底面积;其中,圆柱的体积=长方体的体积=长×宽×高。
7.解:640÷4×
=160×
=100(千米)
答:客车每小时行100千米。
客车的速度=两地之间的距离÷相遇时间×客车速度占的分率。
8.解:设15g消毒液稀释时要x克水。
15:x=1:80
x=15×80
x=1200
答:15g消毒液稀释时要1200克水。
设15g消毒液稀释时要x克水。依据15g消毒液:要加水的质量=1:80列比例,解比例。
9.解:设折150个千纸鹤需要x小时。
60:1.5=150:x
60x=1.5×150
60x=225
x=3.75
答:折150个千纸鹤需要3.75小时。
观察图形可知,每小时折纸鹤的个数不变,折的个数和时间成正比例关系,设折150个纸鹤需要x小时,根据每小时折纸鹤的个数不变列出比例解答即可。
10.解:×3.14×32×4
=×3.14×9×4
=3.14×12
=37.68(立方厘米)
答:这个圆锥的体积是37.68立方厘米。
为轴的这条直角边就是圆锥的高,另一条直角边是圆锥的底面半径,圆锥的体积=底面积×高×,根据公式计算体积即可。
11.解:200÷50%=400(人)
答:该校课外活动小组一共调查了400人。
观察统计图,扇形统计图中D类占总量的50%,条形统计图中D类人数是200人,根据分数除法的意义,用D类的人数除以50%即可求出一共调查的人数。
12.解:设裤子需要x元。
x+2x=360
3x=360
3x÷3=360÷3
x=120
答:裤子需要120元。
等量关系:裤子的价格+上衣价格=360元。设裤子需要x元,则上衣价钱是2x元,根据等量关系列出方程解答即可。
13.解:4+6=10(人)
方案一:
4×160+6×90
=640+540
=1180(元)
方案二:
120×10=1200(元)
1180<1200
答:4位大人带6名小孩,按方案一购票划算。
方案一的总价=儿童票的单价×儿童的人数+成人票的单价×成人的人数;
方案二的总价=团体票的单价×(儿童的人数+成人的人数),然后再比较大小。
14.解:3.14×42
=3.14×16
=50.24(平方米)
3.14×()2×2+×3.14×()2×1.2
=3.14×16×2+3.14×16×0.4
=100.48+20.096
=120.576(立方米)
答:这个蒙古包占地50.24平方米;内部的空间约是120.576立方米。
这个蒙古包占地面积=π×半径2;半径=直径÷2;内部的空间=圆柱的容积+圆锥的容积;其中,圆柱的容积=π×半径2×高,圆锥的容积=π×半径2×高×。
15.解:6000+6000×2.17%×2
=6000+6000×0.0217×2
=6000+260.4
=6260.4(元)
答:到期后他可从银行中提取本金和利息一共6260.4元。
到期后他可从银行中提取本金和利息一共的钱数=本金+利息;其中,利息=本金×利率×存期。
16.解:假设工程总量为100。
20÷4=5
(100﹣20)÷6﹣5
=80÷6﹣5
=13-5
=8
(100﹣15×5)÷8
=25÷8
=3(天)
答:乙还需要4天。
甲工程队先做4天做的工作量÷4=甲工程队每天做的工作量;
总工作量-甲工程队先做的工作量=剩下的工作量,剩下的工作量÷他们共做的时间=他们每天的工作量之和;他们每天的工作量之和-甲工程队每天做的工作量=乙工程队每天做的工作量;
总工作量-甲工程队先做15的工作量=剩下的工作量,剩下的工作量÷乙工程队每天做的工作量=剩下的由乙单独完成还需要的天数。
17.解:第一、二车间的人数占总人数的:1﹣=
第一车间的人数占总人数的:
第二车间的人数占总人数的:
总人数:
300÷()
=300÷
=300×4
=1800(人)
答:这个工厂一共有1800人。
这个工厂的总人数看做单位1,单位1-第三车间的人数占总人数的分率=第一车间第二车间的人数占的分率和;
第一车间与第二车间的人数比是5:3,可以把第一车间的人数看做5份,第二车间的人数看做3份;两个车间一共是8份,第一车间的人数占两个车间人数的,第二车间的人数占两个车间人数的;
两个车间占的分率和×第一车间的人数占两个车间人数的分率和=第一车间的人数占总人数的分率;两个车间占的分率和×第二车间的人数占两个车间人数的分率和=第二车间的人数占总人数的分率;
第一车间比第二车间多的人数÷第一车间比第二车间多占总人数的分率=总人数。
18.解:×3.14×(12.56÷3.14÷2)2×6×2÷5
=×3.14×4×6×2÷5
=25.12×2÷5
=50.24÷5
≈11(次)
答:11次可以运完。
圆锥的底面周长÷π÷2=圆锥的底面半径,×π×圆锥的底面半径的平方×高=圆锥的体积,圆锥的体积×每立方米的沙子重=这堆沙子的重量;这堆沙子的重量÷每次运的重量,商采取进一法得到的整数就是运完至少需要的次数。
19.解:甲品牌:260>200,所以减100元,
260﹣100=160(元)
乙品牌:
260×60%×90%
=156×90%
=140.4(元)
140.4<160
答:乙品牌的更便宜。
甲品牌,超过200元就减去100元,那么原价260的鞋,只需要260-100元;乙品牌,“折上折”,先打六折,在此基础上再打九折,先把原价看成单位“1”,用原价乘上60%,就是六折后的价格,再把六折后的价格看成单位“1”,再乘上90%,机会现价;比较两种品牌的现价即可求解。
20.解:设公鸡养了x只,则母鸡养了(480﹣x)只
x×1.5+30=480﹣x
2.5x=450
x=180
当x=180时,
480﹣x=480﹣180
=300
答:有母鸡300只,公鸡180只。
采用方程解答此题,设公鸡养了x只,因为“饲养场共养480只鸡”,所以养了母鸡(480-x)只,因为“母鸡只数比公鸡只数的1.5倍还多30只”,所以可得等量关系式为:公鸡的只数×1.5+30=母鸡的只数,列方程求解。
21.(1)解:如下表所示:
答:可以设计4种不同的纸盒。
(2)解:22×16×1=352(cm3)
20×14×2=560(cm3)
18×12×3=648(cm3)
16×10×4=640(cm3)
648>640>560>352,即长是18cm,宽是12cm,高是3cm时纸盒的容积最大,最大为648立方厘米。
答:纸盒的最大容积是648立方厘米。
解:(1)四个角分别去掉1个边长1厘米的正方形,折叠后就成了一个无盖的长方体纸盒,长是(24-1-1)厘米,宽是(18-1-1)厘米,高是1厘米;四个角还可以分别去掉边长2厘米、3厘米、4厘米的正方形,按照这样的方法设计不同的纸盒即可;
(2)长方体容积=长×宽×高,分别计算出这几种纸盒的容积,判断容积最大的纸盒即可。
22.解:第一堆:12÷(+﹣1)
=12÷(﹣1)
=45(吨)
第二堆:45×+7
=30+7
=37(吨)
第三堆:45×﹣7
=27﹣7
=20(吨)
答:第一堆石子45吨,第二堆石子37吨,第三堆石子20吨。
如果把第二堆和第三堆的石子合在一起,就刚好比第一堆多(+-1),由此根据分数除法的意义,用第二、三两堆石子质量的和比第一堆多12吨除以多的分率即可求出第一堆石子的质量,进而分别求出第二堆和第三堆石子的质量。
23.解:5.5÷=11000000(厘米)
11000000×=(厘米)
答:这条公路的图上距离是厘米。
比例尺为1:2000000的地图,实际图上距离为5.5厘米,根据实际距离=图上距离÷比例尺,求出这条公路的实际距离;再用实际距离乘另一幅地图的比例尺即可求出另一幅地图上的图上距离。
24.解:3.14×4×3+3.14×(4÷2)2
=12.56×3+3.14×4
=37.68+12.56
=50.24(平方米)
答:抹水泥的面积是50.24平方米。
抹水泥的部分面积=圆柱的侧面积+圆柱的底面积;圆柱的侧面积=底面周长×高;底面积=π×半径2;据此解答。
25.解:10÷2=5(厘米)
×3.14×5×5×6÷10
= ×3.14×25×6÷10
=157÷10
≈16(分钟)
答:按服务员的承诺最迟16分钟后欢欢一家点的菜会上桌。
π×底面半径的平方×高÷3=圆锥的体积;圆锥的体积÷每分钟漏掉沙子的体积=漏完需要的时间。
26.解:300× =100(千米/时)
100÷ =900(千米/时)
答:小汽车的速度是100千米/时,喷气式飞机的速度是900千米/时。
求一个数的几分之几是多少用乘法;已知一个数的几分之几是多少,求这个数用除法。
27.(1)解:行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系。
(2)6.4
(3)解:32÷10=3.2(升)
3.2>3
答:他需要加油。
解:(1)行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系;
(2)64÷10=6.4(升)。
故答案为:(1)行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系;(2)6.4。
(1)行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系;
(2)汽车耗油的升数=从富川县城到贺州园博园的路程÷10;
(3)小军一家游览完贺州园博园后,想驾车去距离姑婆山需要油的升数=路程÷10=3.2升,然后比较大小。
28.(1)200
(2)解:1-15%-45%-21%
=85%-45%-21%
=40%-21%
=19%
200×19%=38(人)
200×45%=90(人)
统计图如下:
(3)90;19
(4)解:我打算多采用步行的方式低碳绿色出行,还锻炼了身体。
解:(1)42÷21%=200(人);
(3)200×45%=90(人)
1-15%-45%-21%
=85%-45%-21%
=40%-21%
=19%。
故答案为:(1)200;(3)90;19。
(1)此次共调查访问的人数=步行的人数÷步行占的百分率;
(2)、(3)自驾车占的百分率=单位“1”-其余各项分别占的百分率;自驾车、骑自行车分别的人数=此次共调查访问的人数×各自分别占的百分率;然后画出直条,并且标上数据;
(4)我打算多采用步行的方式低碳绿色出行,还锻炼了身体。
29.解:0.4公顷=40000000平方厘米
80×40=3200(平方厘米)
40000000÷3200=12500(块)
答:至少需要12500块这样的地砖。
至少需要这样地砖的块数=南堤公园广场的面积÷(长方形地砖的长×宽)。
30.(1)解:
(2)解:
(3)解:
(4)解:6×10000=60000(厘米)
60000厘米=600米
4×10000=40000(厘米)
40000厘米=400米
600×400÷2
=240000÷2
=120000(平方米)
12000平方米=12公顷
答:图③的实际面积是12公顷。
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可;
(3)放大后三角形底、高分别的格数=原来三角形底、高的格数分别×2,然后画出图形;
(4)实际距离=图上距离÷比例尺,③的实际面积=③实际的底×实际的宽÷2,然后单位换算。
小升初数学备考真题分类汇编(广西地区专版)
试卷说明:
本试卷试题精选自广西省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合广西省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、解决问题
1.(2024·南宁)欢欢一家到餐馆吃饭。点完菜后服务员把一个沙漏摆到桌上,并且说“给您计个时,沙漏漏完前您点的菜都会上桌”。
欢欢发现这是一个上下均为圆锥的沙漏(如下图),两个圆锥的底面直径均是10厘米,高均是6厘米。沙漏上面的圆锥中装满沙子,如果每分钟漏掉10立方厘米的沙子,那么按服务员的承诺最迟多少分钟后欢欢﹣家点的菜会上桌?(得数保留整数)
2.(2024·良庆)工人要在一个圆柱形贮水池的侧面和底面抹一层水泥,抹水泥的面积有多少平方米?
3.(2024·博白)某实验小学六⑴班学生在开学体能测试中达标率为85%,经过一个学期的训练,在期末体能测试中达标的人数增加了4人,达标率上升到95%。六⑴班期末体能测试中达标人数是多少人?
4.(2024·港南)为了打造“全国文明城市”,某市计划在一条道路两旁种紫荆树和玉兰树,紫荆树和玉兰树的棵数比是3:2。已知种了600棵紫荆树,需要种多少棵玉兰树?
5.(2024·南宁)最是书香能宜人,今年的4月23日,是第29个“世界读书日”。学校为同学们准备了丰盛的读书日“大餐”。赵丽读了一本学校推荐的书,如果平均每天读25页,那么8天可以读完;如果赵丽想10天读完,那么平均每天读多少页?(用比例解)
6.(2024·良庆)把一块长方体铁块熔铸成一个底面半径为4dm的圆柱形铁块。这个圆柱形铁块的高是多少?
7.(2024·良庆)客车和货车同时从相距640千米的两地出发,相向而行,经过4小时相遇。已知客车和货车的速度比是5:3,客车每小时行多少千米?
8.(2024·良庆)某消毒液用于衣物消毒时需要用水按1:80稀释。15g消毒液稀释时要多少克水?(用比例解)
9.(2024·博白)小红折一些千纸鹤,时间和折千纸鹤个数的关系如下图。折150个千纸鹤需要多少小时?(用比例的知识解答)
10.(2024·博白)如下图,ABC是直角三角形,以AB为轴,将三角形绕这条轴旋转一周,得到一个圆锥,这个圆锥的体积是多少立方厘米?
11.(2024·博白)每年的6月5日是“世界环境日“。某校课外活动小组对部分师生开展了以“爱护环境,从我做起”为主题的问卷调查活动。师生对垃圾的处理方式有:A.随手乱扔垃圾;B.偶尔会将垃圾丢在垃圾桶;C.能将垃圾丢在垃圾桶,但不会考虑垃圾分类;D.能将垃圾丢在垃圾桶,而且还会考虑垃圾分类。
该小组将调查结果整理后,制成如下两个统计图。
该校课外活动小组一共调查了多少人?
12.(2024·博白)“六一”儿童节,妈妈给小丽买了一套新衣服,一共用了360元,已知上衣的价钱是裤子的2倍,裤子需要多少元?
13.(2024·港南)某旅行社五一期间推出“北帝山景区一日游”两种购票方案。如果4位大人带6名小孩,怎样购票划算?
方案一: 成人票价160元/人 儿童票价90元/人 方案二: 团体10人以上(包括10人)票价120元/人
14.(2024·港南)蒙古包也称“毡包”,是蒙古族传统民居,如图中的蒙古包是由一个圆柱体和一个圆锥体组成的(单位:米)。这个蒙古包占地多少?内部的空间约是多少?
15.(2024·港南)如下是一张银行定期储蓄存单相关信息,请你帮李军算算到期后他可从银行中提取本金和利息一共多少元?
户名:李军 存期:两年年利率:2.17% 存入日期:2022年7月4日 存入金额:陆仟元整 到期日期:2024年7月4日
16.(2023·南宁)一项工程,甲工程队先做4天,完成了工程的20%,又共做了6天才完成全部工程。如果这项工程甲先做15天,剩下的由乙单独完成,乙还需要多少天?
17.(2023·南宁)一个工厂有三个车间,第一车间与第二车间的人数比是5:3,第三车间的人数占全厂职工人数的,已知第一车间比第二车间多300人,这个工厂一共有多少人?
18.(2023·南宁)一个圆锥形地沙堆,底面周长是12.56米,高6米,已知每立方米的沙子重2吨,如果用一辆载重量为5吨地汽车去运,多少次可以远完?(π取3.14)
19.(2023·南宁)百货大楼搞促销活动,甲品牌鞋满200元减100元,乙品牌鞋“折上折”,就是先打六折,在此基础上再打九折。如果两个品牌都有一双标价260元的鞋,哪个品牌的更便宜?
20.(2023·南宁)饲养场共养480只鸡。母鸡只数比公鸡只数的1.5倍还多30只,公鸡、母鸡各养了多少只?
21.(2023·灵山)小明准备用如图所示的长方形纸板做一个长方体无盖纸盒。
(1)如果纸盒的高都是整厘米数,可以设计几种不同的纸盒?
(2)在你找到的不同设计方案中,纸盒的最大容积是多少立方厘米?(纸板的厚度忽略不计)
22.(2023·灵山)建筑工地运来三堆石子,第二堆比第一堆的多7吨,第三堆比第一堆的少7吨。如果第二、三两堆石子质量的和比第一堆多12吨,三堆石子各多少吨?
23.(2023·武鸣)在一幅比例尺是1:2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5厘米.在另一幅比例尺是1:15000000的地图上,这条公路的图上距离是多少?
24.(2023·武鸣)修建一个圆柱形的沼气池。底面直径是4m,深3m。在池的侧面与下底面抹上水泥。抹水泥部分的面积是多少平方米?
25.(2023·青秀)欢欢一家到餐馆吃饭。点完菜后服务员把一个沙漏摆到桌上,并且说“给您计个时,沙漏漏完前您点的菜都会上桌”。
欢欢发现这是一个上下均为圆锥的沙漏(如图),两个圆锥的底面直径均是10厘米,高均是6厘米。沙漏上面的圆锥中装满沙子,如果每分钟漏掉10立方厘米的沙子,那么按服务员的承诺最迟多少分钟后欢欢一家点的菜会上桌?(得数保留整数)
26.(2023·青秀)“和谐号”动车组的速度可达300km/h,小汽车的速度是“和谐号”速度的 ,是一架喷气式飞机的 。小汽车和喷气式飞机的速度分别是多少?
27.(2023·贺州)贺州园博园位于贺江南岸,莲塘镇与鹅塘镇交界处,以“山水贺寿,诗意乡愁”为主题,意境极富诗意,吸引了大批游客前来观光。“五一”节,小军一家驾车从富川县城到贺州园博园参观。如图表示的是开车从富川县城到贺州园博园行驶的路程与耗油量之间的关系。
(1)行驶的路程和耗油量成什么比例关系?请说明理由。 。
(2)从富川县城到贺州园博园的路程有64km,汽车耗油 L。
(3)小军一家游览完贺州园博园后,想驾车去距离32km的姑婆山。此时油箱里大约剩下3L汽油,算一算,他们需要加油吗?
28.(2023·贺州)绿色生态是我们贺州最亮丽的底色,而绿色出行是保护贺州“绿色环保生态文明”最有效的方式之一。为此,我们开展“绿色低碳文明出行”调查访问活动,如图是调查某公司职员的出行方式后,制成的两幅统计图。
(1)本次“绿色低碳文明出行”调查活动一共调查访问了 人。
(2)请你将统计图补充完整。
(3)骑自行车出行的有 人,自驾车出行的占 %。
(4)文明健康新风尚,绿色环保我先行,观察如图的数据,你打算如何行动?
29.(2023·贺州)为进一步提升寿城群众幸福感,寿城贺州在加快城市公园建设步伐,目前在建的南堤公园广场面积大约0.4公顷,如果用长80cm,宽40cm的长方形地砖铺地,至少需要用多少块这样的地砖?
30.(2023·贺州)如图中每个小方格的边长代表1厘米。
(1)在方格纸上找出点A(4,6)、B(2,3),C(4,3)并将三点连接起来形成三角形①;
(2)画出把三角形①绕C点顺时针旋转90°后得到的图②;
(3)画出把图②按2:1放大后得到的图③;
(4)根据比例尺计算出图③的实际面积是多少公顷。
答案解析部分
1.解:×3.14×(10÷2)2×6÷10
=×3.14×25×6÷10
=157÷10
≈16(分钟)
答:按服务员的承诺最迟16分钟后欢欢一家点的菜会上桌。
按服务员的承诺欢欢一家点的菜会上桌最迟需要的时间=×π×半径2×高÷平均每分钟漏掉沙子的体积。
2.解:3.14×4×2×5+3.14×42
=3.14×40+3.14×16
=3.14×(40+16)
=3.14×56
=175.84(平方米)
答:抹水泥的面积有175.84平方米。
抹水泥的面积=π×半径×2×高+π×半径2。
3.解:4÷(95%﹣85%)×95%
=4÷0.1×0.95
=40×0.95
=38(人)
答:六(1)班期末体能测试中达标人数是38人。
根据分数除法的意义,用增加的4人除以增加的百分率即可求出总人数,用总人数乘95%即可求出达标的人数。
4.解:设需要种x棵玉兰树。
600:x=3:2
3x=1200
x=400
答:要种400棵玉兰树。
设需要种x棵玉兰树。 依据种紫荆树的棵数:需要种玉兰树的棵数=3:2,列比例,解比例。
5.解:设平均每天要读x页。
10x=25×8
10x=200
10x÷10=200÷10
x=20
答:平均每天读20页。
设平均每天要读x页。依据赵丽想读完的天数×平均每天要读的页数=计划平均每天读的页数×计划读的天数,列比例,解比例。
6.解:18.84×8×6÷(3.14×42)
=904.32÷50.24
=18(分米)
答:这个圆柱铁块的高是18分米。
这个圆柱铁块的高=圆柱的体积÷圆柱的底面积;其中,圆柱的体积=长方体的体积=长×宽×高。
7.解:640÷4×
=160×
=100(千米)
答:客车每小时行100千米。
客车的速度=两地之间的距离÷相遇时间×客车速度占的分率。
8.解:设15g消毒液稀释时要x克水。
15:x=1:80
x=15×80
x=1200
答:15g消毒液稀释时要1200克水。
设15g消毒液稀释时要x克水。依据15g消毒液:要加水的质量=1:80列比例,解比例。
9.解:设折150个千纸鹤需要x小时。
60:1.5=150:x
60x=1.5×150
60x=225
x=3.75
答:折150个千纸鹤需要3.75小时。
观察图形可知,每小时折纸鹤的个数不变,折的个数和时间成正比例关系,设折150个纸鹤需要x小时,根据每小时折纸鹤的个数不变列出比例解答即可。
10.解:×3.14×32×4
=×3.14×9×4
=3.14×12
=37.68(立方厘米)
答:这个圆锥的体积是37.68立方厘米。
为轴的这条直角边就是圆锥的高,另一条直角边是圆锥的底面半径,圆锥的体积=底面积×高×,根据公式计算体积即可。
11.解:200÷50%=400(人)
答:该校课外活动小组一共调查了400人。
观察统计图,扇形统计图中D类占总量的50%,条形统计图中D类人数是200人,根据分数除法的意义,用D类的人数除以50%即可求出一共调查的人数。
12.解:设裤子需要x元。
x+2x=360
3x=360
3x÷3=360÷3
x=120
答:裤子需要120元。
等量关系:裤子的价格+上衣价格=360元。设裤子需要x元,则上衣价钱是2x元,根据等量关系列出方程解答即可。
13.解:4+6=10(人)
方案一:
4×160+6×90
=640+540
=1180(元)
方案二:
120×10=1200(元)
1180<1200
答:4位大人带6名小孩,按方案一购票划算。
方案一的总价=儿童票的单价×儿童的人数+成人票的单价×成人的人数;
方案二的总价=团体票的单价×(儿童的人数+成人的人数),然后再比较大小。
14.解:3.14×42
=3.14×16
=50.24(平方米)
3.14×()2×2+×3.14×()2×1.2
=3.14×16×2+3.14×16×0.4
=100.48+20.096
=120.576(立方米)
答:这个蒙古包占地50.24平方米;内部的空间约是120.576立方米。
这个蒙古包占地面积=π×半径2;半径=直径÷2;内部的空间=圆柱的容积+圆锥的容积;其中,圆柱的容积=π×半径2×高,圆锥的容积=π×半径2×高×。
15.解:6000+6000×2.17%×2
=6000+6000×0.0217×2
=6000+260.4
=6260.4(元)
答:到期后他可从银行中提取本金和利息一共6260.4元。
到期后他可从银行中提取本金和利息一共的钱数=本金+利息;其中,利息=本金×利率×存期。
16.解:假设工程总量为100。
20÷4=5
(100﹣20)÷6﹣5
=80÷6﹣5
=13-5
=8
(100﹣15×5)÷8
=25÷8
=3(天)
答:乙还需要4天。
甲工程队先做4天做的工作量÷4=甲工程队每天做的工作量;
总工作量-甲工程队先做的工作量=剩下的工作量,剩下的工作量÷他们共做的时间=他们每天的工作量之和;他们每天的工作量之和-甲工程队每天做的工作量=乙工程队每天做的工作量;
总工作量-甲工程队先做15的工作量=剩下的工作量,剩下的工作量÷乙工程队每天做的工作量=剩下的由乙单独完成还需要的天数。
17.解:第一、二车间的人数占总人数的:1﹣=
第一车间的人数占总人数的:
第二车间的人数占总人数的:
总人数:
300÷()
=300÷
=300×4
=1800(人)
答:这个工厂一共有1800人。
这个工厂的总人数看做单位1,单位1-第三车间的人数占总人数的分率=第一车间第二车间的人数占的分率和;
第一车间与第二车间的人数比是5:3,可以把第一车间的人数看做5份,第二车间的人数看做3份;两个车间一共是8份,第一车间的人数占两个车间人数的,第二车间的人数占两个车间人数的;
两个车间占的分率和×第一车间的人数占两个车间人数的分率和=第一车间的人数占总人数的分率;两个车间占的分率和×第二车间的人数占两个车间人数的分率和=第二车间的人数占总人数的分率;
第一车间比第二车间多的人数÷第一车间比第二车间多占总人数的分率=总人数。
18.解:×3.14×(12.56÷3.14÷2)2×6×2÷5
=×3.14×4×6×2÷5
=25.12×2÷5
=50.24÷5
≈11(次)
答:11次可以运完。
圆锥的底面周长÷π÷2=圆锥的底面半径,×π×圆锥的底面半径的平方×高=圆锥的体积,圆锥的体积×每立方米的沙子重=这堆沙子的重量;这堆沙子的重量÷每次运的重量,商采取进一法得到的整数就是运完至少需要的次数。
19.解:甲品牌:260>200,所以减100元,
260﹣100=160(元)
乙品牌:
260×60%×90%
=156×90%
=140.4(元)
140.4<160
答:乙品牌的更便宜。
甲品牌,超过200元就减去100元,那么原价260的鞋,只需要260-100元;乙品牌,“折上折”,先打六折,在此基础上再打九折,先把原价看成单位“1”,用原价乘上60%,就是六折后的价格,再把六折后的价格看成单位“1”,再乘上90%,机会现价;比较两种品牌的现价即可求解。
20.解:设公鸡养了x只,则母鸡养了(480﹣x)只
x×1.5+30=480﹣x
2.5x=450
x=180
当x=180时,
480﹣x=480﹣180
=300
答:有母鸡300只,公鸡180只。
采用方程解答此题,设公鸡养了x只,因为“饲养场共养480只鸡”,所以养了母鸡(480-x)只,因为“母鸡只数比公鸡只数的1.5倍还多30只”,所以可得等量关系式为:公鸡的只数×1.5+30=母鸡的只数,列方程求解。
21.(1)解:如下表所示:
答:可以设计4种不同的纸盒。
(2)解:22×16×1=352(cm3)
20×14×2=560(cm3)
18×12×3=648(cm3)
16×10×4=640(cm3)
648>640>560>352,即长是18cm,宽是12cm,高是3cm时纸盒的容积最大,最大为648立方厘米。
答:纸盒的最大容积是648立方厘米。
解:(1)四个角分别去掉1个边长1厘米的正方形,折叠后就成了一个无盖的长方体纸盒,长是(24-1-1)厘米,宽是(18-1-1)厘米,高是1厘米;四个角还可以分别去掉边长2厘米、3厘米、4厘米的正方形,按照这样的方法设计不同的纸盒即可;
(2)长方体容积=长×宽×高,分别计算出这几种纸盒的容积,判断容积最大的纸盒即可。
22.解:第一堆:12÷(+﹣1)
=12÷(﹣1)
=45(吨)
第二堆:45×+7
=30+7
=37(吨)
第三堆:45×﹣7
=27﹣7
=20(吨)
答:第一堆石子45吨,第二堆石子37吨,第三堆石子20吨。
如果把第二堆和第三堆的石子合在一起,就刚好比第一堆多(+-1),由此根据分数除法的意义,用第二、三两堆石子质量的和比第一堆多12吨除以多的分率即可求出第一堆石子的质量,进而分别求出第二堆和第三堆石子的质量。
23.解:5.5÷=11000000(厘米)
11000000×=(厘米)
答:这条公路的图上距离是厘米。
比例尺为1:2000000的地图,实际图上距离为5.5厘米,根据实际距离=图上距离÷比例尺,求出这条公路的实际距离;再用实际距离乘另一幅地图的比例尺即可求出另一幅地图上的图上距离。
24.解:3.14×4×3+3.14×(4÷2)2
=12.56×3+3.14×4
=37.68+12.56
=50.24(平方米)
答:抹水泥的面积是50.24平方米。
抹水泥的部分面积=圆柱的侧面积+圆柱的底面积;圆柱的侧面积=底面周长×高;底面积=π×半径2;据此解答。
25.解:10÷2=5(厘米)
×3.14×5×5×6÷10
= ×3.14×25×6÷10
=157÷10
≈16(分钟)
答:按服务员的承诺最迟16分钟后欢欢一家点的菜会上桌。
π×底面半径的平方×高÷3=圆锥的体积;圆锥的体积÷每分钟漏掉沙子的体积=漏完需要的时间。
26.解:300× =100(千米/时)
100÷ =900(千米/时)
答:小汽车的速度是100千米/时,喷气式飞机的速度是900千米/时。
求一个数的几分之几是多少用乘法;已知一个数的几分之几是多少,求这个数用除法。
27.(1)解:行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系。
(2)6.4
(3)解:32÷10=3.2(升)
3.2>3
答:他需要加油。
解:(1)行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系;
(2)64÷10=6.4(升)。
故答案为:(1)行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系;(2)6.4。
(1)行驶路程与耗油量的比值是一定的,所以汽车行驶路程与耗油量是正比例关系;
(2)汽车耗油的升数=从富川县城到贺州园博园的路程÷10;
(3)小军一家游览完贺州园博园后,想驾车去距离姑婆山需要油的升数=路程÷10=3.2升,然后比较大小。
28.(1)200
(2)解:1-15%-45%-21%
=85%-45%-21%
=40%-21%
=19%
200×19%=38(人)
200×45%=90(人)
统计图如下:
(3)90;19
(4)解:我打算多采用步行的方式低碳绿色出行,还锻炼了身体。
解:(1)42÷21%=200(人);
(3)200×45%=90(人)
1-15%-45%-21%
=85%-45%-21%
=40%-21%
=19%。
故答案为:(1)200;(3)90;19。
(1)此次共调查访问的人数=步行的人数÷步行占的百分率;
(2)、(3)自驾车占的百分率=单位“1”-其余各项分别占的百分率;自驾车、骑自行车分别的人数=此次共调查访问的人数×各自分别占的百分率;然后画出直条,并且标上数据;
(4)我打算多采用步行的方式低碳绿色出行,还锻炼了身体。
29.解:0.4公顷=40000000平方厘米
80×40=3200(平方厘米)
40000000÷3200=12500(块)
答:至少需要12500块这样的地砖。
至少需要这样地砖的块数=南堤公园广场的面积÷(长方形地砖的长×宽)。
30.(1)解:
(2)解:
(3)解:
(4)解:6×10000=60000(厘米)
60000厘米=600米
4×10000=40000(厘米)
40000厘米=400米
600×400÷2
=240000÷2
=120000(平方米)
12000平方米=12公顷
答:图③的实际面积是12公顷。
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可;
(3)放大后三角形底、高分别的格数=原来三角形底、高的格数分别×2,然后画出图形;
(4)实际距离=图上距离÷比例尺,③的实际面积=③实际的底×实际的宽÷2,然后单位换算。
同课章节目录
