3.2.2 双曲线的简单几何性质(第2课时)教学课件(共22张PPT)人教A版高中数学(2019)选择性必修一
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质(第2课时)教学课件(共22张PPT)人教A版高中数学(2019)选择性必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
3.2.2 双曲线的简单几何性质(第2课时)
3.2 双曲线
复习回顾
双曲线的概念及其标准方程
定义:一般地,我们把平面内与两个定点 , 的距离的差的绝对值等于非零常数(小于 )的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间距离叫做双曲线的焦距.
焦点在 轴上:
焦点在 轴上:
复习回顾
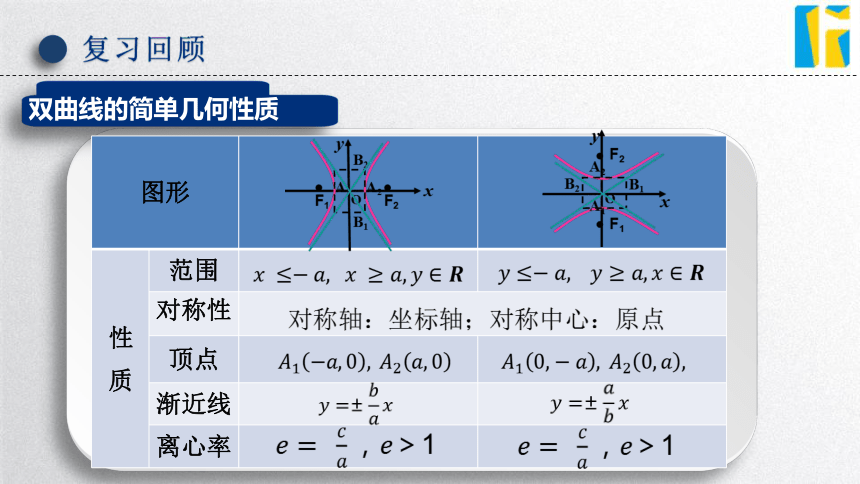
双曲线的简单几何性质
图形
性 质 范围
对称性 顶点
渐近线
离心率
环节一:实际问题,建模双曲线
例4
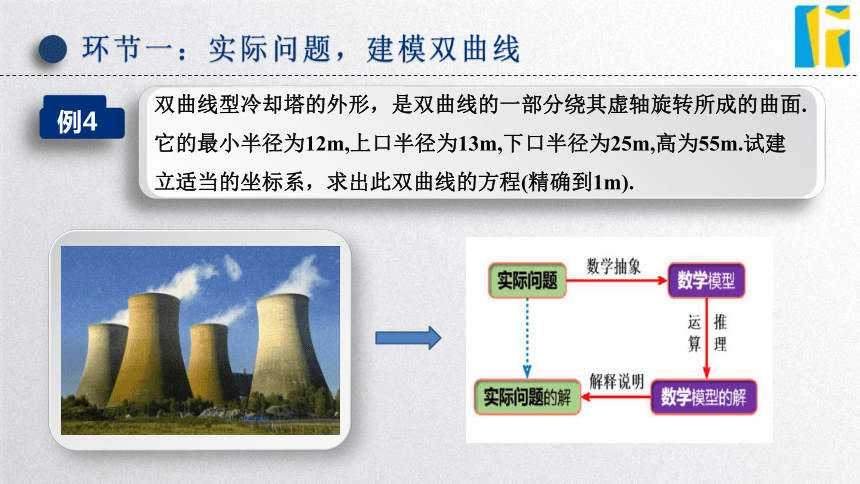
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
环节一:实际问题,建模双曲线
例4
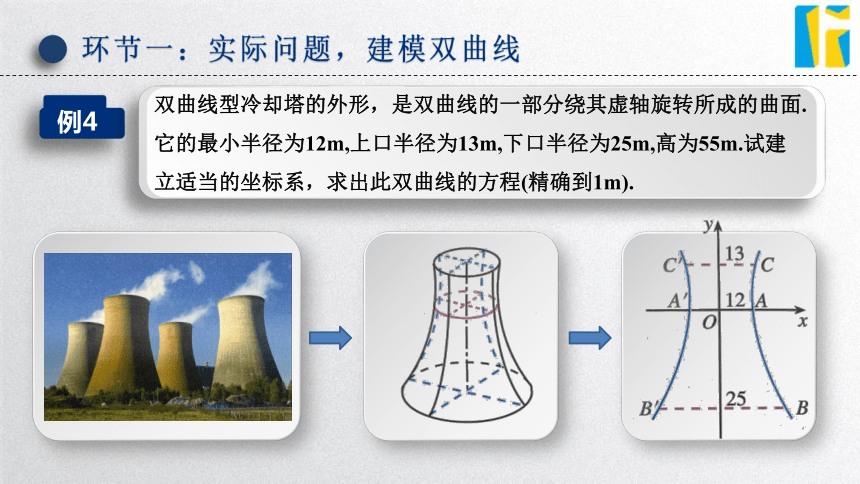
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立直角坐标系Oxy,使小圆的直径AA'在x轴上,圆心与原点重合.这时,上、下口的直径都平行于x轴,且 |CC'|=13×2 , |BB'|=25×2.
环节一:实际问题,建模双曲线
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
设双曲线的方程为
点C的坐标为(13,y),则点B的坐标为(25,y-55).
因为直径AA'实轴,所以a=12.又B,C两点都在双曲线上,所以
①
②
环节一:实际问题,建模双曲线
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
由方程②,得 (负值舍去).
代入方程①,得
化简得 19b2+275b-18150=0. ③
解方程 ③,得 b≈25(负值舍去)
因此所求双曲线的方程为
环节一:实际问题,建模双曲线
归纳总结
解决和双曲线有关的实际问题的思路:
(1)转化:将冷却塔问题抽象成双曲线问题并作简图;
(2)建系:根据要求合理建立平面直角坐标系,并求出相关点坐标;
(3)求解:利用待定系数法求解双曲线问题;
(4)解释:通过结果对冷却塔问题进行解释、说明.
环节一:数学建模,实际应用
环节二:探索发现,再识双曲线
例5
动点 与定点 的距离和它到定直线 的距离的比是常数 ,求动点 的轨迹.
F
O
x
y
l
d
M
H
环节二:探索发现,再识双曲线
概念新知
环节二:探索发现,再识双曲线
双曲线的第二定义:
平面内,如果动点M到定点F的距离与M到定直线l(不过点F)的距离之比为常数 (e>1),那么点M的轨迹为双曲线,
其中定点是双曲线的焦点,定直线是双曲线的准线,
常数e是双曲线的离心率.
思考
通过上述分析,对比上一单元椭圆的一般结论,得到什么猜想?
环节二:探索发现,再识双曲线
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离的比是常数
求动点M的轨迹.
例5
环节二:探索发现,再识双曲线
圆锥曲线的统一定义:
例6
如图,过双曲线 的右焦点 ,倾斜角为 的直线交双曲线于A,B两点,求 .
环节三:类比研究,探索发现
归纳总结
求弦长问题的方法:
(1)如果交点坐标易求,可直接用两点间的距离公式代入求弦长;
(2)有时为了简化计算,常采用设而不求法,运用韦达定理来处理.
环节三:类比研究,探索发现
变式
若将例6中直线的斜率改为2,求 ,请你先画图.
解:设直线AB的方程为
设A,B的坐标为(x1,y1) 、(x2,y2),则
与双曲线方程联立消去y,得
由弦长公式得
环节三:类比研究,探索发现
O
x
y
思维上升
直线与双曲线位置关系:
环节三:类比研究,探索发现
X
Y
O
题型三:求弦长
思维上升
判断直线与双曲线位置关系的处理程序:
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
本节小结
1、双曲线的第二定义;
2、直线双曲线的位置关系;
3、数学思想方法:待定系数法,方程的思想、数形结合思想;
4、数学核心素养:数学建模、数学抽象和数学运算素养.
课后作业
必做 1.课本 P127页:第3题 P127页习题3.2:第6题,综合运用第7、9、10题
探究作业:
设动点M与定点F(c,0) (c>0)的距离和它到定直线l: 的距离的比是常数 (c> a> 0), 求动点M的轨迹方程, 并说明轨迹的形状. 结合教科书第116页“用信息技术探究点的轨迹: 椭圆”,
你还能提出什么问题
感谢
T H A N K S !
下节,精彩继续……
3.2.2 双曲线的简单几何性质(第2课时)
3.2 双曲线
复习回顾
双曲线的概念及其标准方程
定义:一般地,我们把平面内与两个定点 , 的距离的差的绝对值等于非零常数(小于 )的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间距离叫做双曲线的焦距.
焦点在 轴上:
焦点在 轴上:
复习回顾
双曲线的简单几何性质
图形
性 质 范围
对称性 顶点
渐近线
离心率
环节一:实际问题,建模双曲线
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
环节一:实际问题,建模双曲线
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立直角坐标系Oxy,使小圆的直径AA'在x轴上,圆心与原点重合.这时,上、下口的直径都平行于x轴,且 |CC'|=13×2 , |BB'|=25×2.
环节一:实际问题,建模双曲线
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
设双曲线的方程为
点C的坐标为(13,y),则点B的坐标为(25,y-55).
因为直径AA'实轴,所以a=12.又B,C两点都在双曲线上,所以
①
②
环节一:实际问题,建模双曲线
例4
双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
由方程②,得 (负值舍去).
代入方程①,得
化简得 19b2+275b-18150=0. ③
解方程 ③,得 b≈25(负值舍去)
因此所求双曲线的方程为
环节一:实际问题,建模双曲线
归纳总结
解决和双曲线有关的实际问题的思路:
(1)转化:将冷却塔问题抽象成双曲线问题并作简图;
(2)建系:根据要求合理建立平面直角坐标系,并求出相关点坐标;
(3)求解:利用待定系数法求解双曲线问题;
(4)解释:通过结果对冷却塔问题进行解释、说明.
环节一:数学建模,实际应用
环节二:探索发现,再识双曲线
例5
动点 与定点 的距离和它到定直线 的距离的比是常数 ,求动点 的轨迹.
F
O
x
y
l
d
M
H
环节二:探索发现,再识双曲线
概念新知
环节二:探索发现,再识双曲线
双曲线的第二定义:
平面内,如果动点M到定点F的距离与M到定直线l(不过点F)的距离之比为常数 (e>1),那么点M的轨迹为双曲线,
其中定点是双曲线的焦点,定直线是双曲线的准线,
常数e是双曲线的离心率.
思考
通过上述分析,对比上一单元椭圆的一般结论,得到什么猜想?
环节二:探索发现,再识双曲线
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离的比是常数
求动点M的轨迹.
例5
环节二:探索发现,再识双曲线
圆锥曲线的统一定义:
例6
如图,过双曲线 的右焦点 ,倾斜角为 的直线交双曲线于A,B两点,求 .
环节三:类比研究,探索发现
归纳总结
求弦长问题的方法:
(1)如果交点坐标易求,可直接用两点间的距离公式代入求弦长;
(2)有时为了简化计算,常采用设而不求法,运用韦达定理来处理.
环节三:类比研究,探索发现
变式
若将例6中直线的斜率改为2,求 ,请你先画图.
解:设直线AB的方程为
设A,B的坐标为(x1,y1) 、(x2,y2),则
与双曲线方程联立消去y,得
由弦长公式得
环节三:类比研究,探索发现
O
x
y
思维上升
直线与双曲线位置关系:
环节三:类比研究,探索发现
X
Y
O
题型三:求弦长
思维上升
判断直线与双曲线位置关系的处理程序:
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
本节小结
1、双曲线的第二定义;
2、直线双曲线的位置关系;
3、数学思想方法:待定系数法,方程的思想、数形结合思想;
4、数学核心素养:数学建模、数学抽象和数学运算素养.
课后作业
必做 1.课本 P127页:第3题 P127页习题3.2:第6题,综合运用第7、9、10题
探究作业:
设动点M与定点F(c,0) (c>0)的距离和它到定直线l: 的距离的比是常数 (c> a> 0), 求动点M的轨迹方程, 并说明轨迹的形状. 结合教科书第116页“用信息技术探究点的轨迹: 椭圆”,
你还能提出什么问题
感谢
T H A N K S !
下节,精彩继续……
