3.2.1 双曲线及其标准方程 教学课件(共34张PPT)人教A版高中数学(2019)选择性必修一
文档属性
| 名称 | 3.2.1 双曲线及其标准方程 教学课件(共34张PPT)人教A版高中数学(2019)选择性必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
3.2.1 双曲线及其标准方程
3.2 双曲线
学 科:人教A版高中数学选择性必修第一册
年 级:高 二
环节一 创设情境 提出问题
我们知道,平面内与两个定点的距离的和等于常数(大于)的点的轨迹是椭圆.
一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?
问题1
环节一 创设情境 提出问题
环节二 问题探究 形成定义
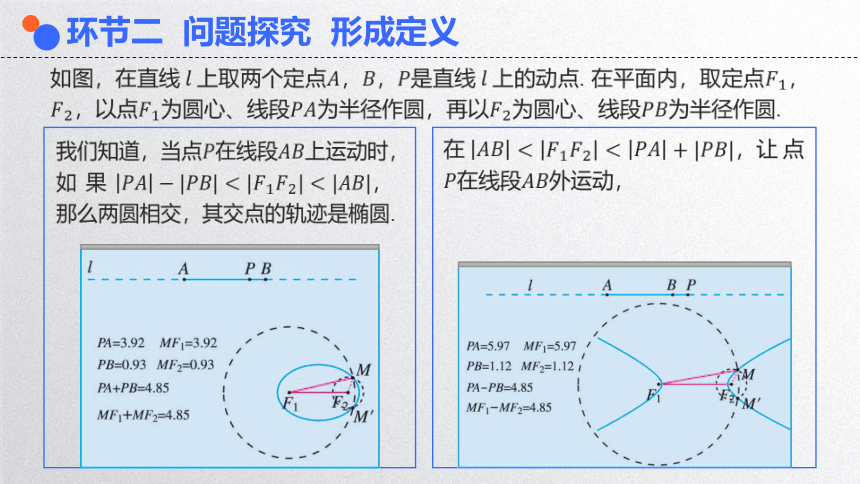
如图,在直线上取两个定点是直线上的动点. 在平面内,取定点,以点为圆心、线段为半径作圆,再以为圆心、线段为半径作圆.
我们知道,当点在线段上运动时,如果那么两圆相交,其交点的轨迹是什么形状.
在点在线段外运动,这时动点满足什么几何条件?两圆交点的轨迹是什么形状?
环节二 问题探究 形成定义
小组展示
如图,在直线上取两个定点是直线上的动点. 在平面内,取定点,以点为圆心、线段为半径作圆,再以为圆心、线段为半径作圆.
我们知道,当点在线段上运动时,如果那么两圆相交,其交点的轨迹是椭圆.
在点在线段外运动,
环节二 问题探究 形成定义
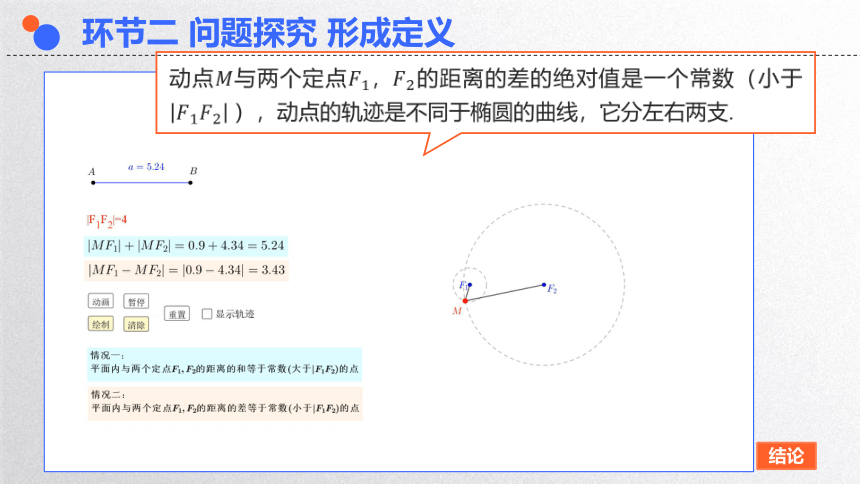
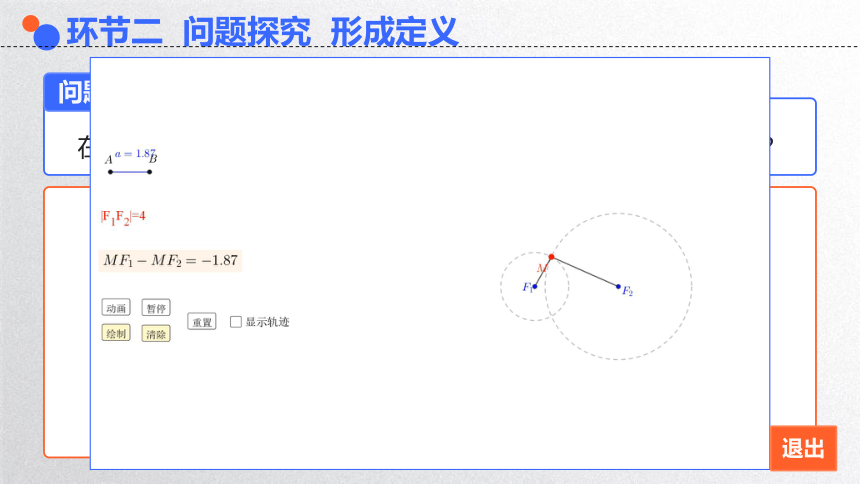
结论
动点与两个定点的距离的差的绝对值是一个常数(小于),动点的轨迹是不同于椭圆的曲线,它分左右两支.
环节二 问题探究 形成定义
双曲线的定义
一般地,我们把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线. 这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
在双曲线的定义中,若去掉“绝对值”,其轨迹还是双曲线吗?
问题4
在双曲线的定义中,若去掉“非零”,其轨迹还是双曲线吗?
问题2
问题3
在双曲线的定义中,常数为什么要小于
环节二 问题探究 形成定义
不是,其轨迹是双曲线的一支.
在双曲线的定义中,若去掉“绝对值”,其轨迹还是双曲线吗?
问题2
结论
观看动态演示
退出
环节二 问题探究 形成定义
当常数等于零时,即
在双曲线的定义中,若去掉“非零”,其轨迹还是双曲线吗?
问题3
这时,动点的轨迹为线段的垂直平分线.
环节二 问题探究 形成定义
①如果定义中常数改为等于,此时动点的轨迹是以 为端点的两条射线(包括端点).
在双曲线的定义中,常数为什么要小于
问题4
②如果定义中常数改为大于 ,此时动点的轨迹不存在.
环节二 问题探究 形成定义
双曲线的定义
一般地,我们把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
回顾椭圆的标准方程的推导步骤及方法,能否类比推导双曲线的标准方程?
问题5
双曲线
环节三 探究运算 建立方程
观察双曲线的形状,如何建立适当的平面直角坐标系?
追问
01
环节三 探究运算 建立方程
如何用坐标表示双曲线上的点所满足的几何条件?
追问
02
双曲线的焦距为,
环节三 探究运算 建立方程
设是双曲线上任意一点,
则焦点的坐标分别为
如何写出曲线上的点所满足条件的集合?
追问
03
设 (为大于的常数,).
由双曲线的定义,双曲线就是下列点的集合:
环节三 探究运算 建立方程
根据点的坐标满足条件的集合写出方程.
因为 ,
类比椭圆标准方程的化简过程,化简①
所以 ①
环节三 探究运算 建立方程
将方程①左边的一个根式移到右边,得
对上式两边平方,得
整理,得
对上式两边平方,整理得
两边同时除以,得
环节三 探究运算 建立方程
由双曲线的定义知,,即,所以.
类比椭圆标准方程的建立过程,令 ,其中 ,代入上式,得
②
我们称方程②是双曲线的方程,这个方程叫做双曲线的标准方程. 它表示焦点在轴上,焦点分别是的双曲线,这里.
环节三 探究运算 建立方程
类比椭圆,焦点在轴上的双曲线的标准方程是什么?
问题6
双曲线的焦距为,焦点分别是,的意义同上,这时双曲线的方程是
这个方程也是双曲线的标准方程.
环节三 探究运算 建立方程
双曲线中的关系与椭圆中的关系有何不同?
问题7
双曲线标准方程中:,其中
与的大小关系不确定;
椭圆标准方程中,,其中,
环节三 探究运算 建立方程
观察双曲线的两种标准方程如何判断焦点所在的坐标轴?
问题8
谁的系数为正,焦点落在哪条轴上,分母为,反之亦然.
环节三 探究运算 建立方程
椭圆、双曲线标准方程的比较
椭圆及其标准方程 双曲线及其标准方程
定义式
abc的关系
焦点在轴上
焦点在轴上
椭圆、双曲线标准方程的比较
椭圆及其标准方程 双曲线及其标准方程
定义式
abc的关系
焦点在轴上
焦点在轴上
环节四 例题练习 巩固理解
例
已知双曲线的两个焦点分别为,双曲线上一点与, 的距离差的绝对值等于,求双曲线的标准方程.
解:
由于双曲线的焦点在轴上,所以设它的标准方程为
由,,得,又,因此 .
所以,双曲线的标准方程为
跟踪练习
根据条件写出双曲线标准方程.
①焦点为
②焦点为,且经过点
环节四 例题练习 巩固理解
链接高考
(2021年新高考Ⅰ卷·第21题)
在平面直角坐标系中,已知点 ,点M的轨迹为C.
(1)求C的方程;
环节四 例题练习 巩固理解
环节五:课堂小结 思维导图
双曲线及其标准方程
双曲线的定义
双曲线的标准方程
双曲线标准方程的求法及应用
知识内容:
思想方法
待定系数法
分类讨论
数形结合思想
类比
核心素养
数学抽象
双曲线的定义.
逻辑推理
运用定义推导双曲线的标准方程.
数学运算
双曲线标准方程的求法.
环节五:课堂小结 思维导图
必 做 课本P127:1、2、5、7
探究作业: 课本P121探究
环节六:课后作业 巩固提升
感谢
T H A N K S !
下节,精彩继续……
3.2.1 双曲线及其标准方程
3.2 双曲线
学 科:人教A版高中数学选择性必修第一册
年 级:高 二
环节一 创设情境 提出问题
我们知道,平面内与两个定点的距离的和等于常数(大于)的点的轨迹是椭圆.
一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?
问题1
环节一 创设情境 提出问题
环节二 问题探究 形成定义
如图,在直线上取两个定点是直线上的动点. 在平面内,取定点,以点为圆心、线段为半径作圆,再以为圆心、线段为半径作圆.
我们知道,当点在线段上运动时,如果那么两圆相交,其交点的轨迹是什么形状.
在点在线段外运动,这时动点满足什么几何条件?两圆交点的轨迹是什么形状?
环节二 问题探究 形成定义
小组展示
如图,在直线上取两个定点是直线上的动点. 在平面内,取定点,以点为圆心、线段为半径作圆,再以为圆心、线段为半径作圆.
我们知道,当点在线段上运动时,如果那么两圆相交,其交点的轨迹是椭圆.
在点在线段外运动,
环节二 问题探究 形成定义
结论
动点与两个定点的距离的差的绝对值是一个常数(小于),动点的轨迹是不同于椭圆的曲线,它分左右两支.
环节二 问题探究 形成定义
双曲线的定义
一般地,我们把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线. 这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
在双曲线的定义中,若去掉“绝对值”,其轨迹还是双曲线吗?
问题4
在双曲线的定义中,若去掉“非零”,其轨迹还是双曲线吗?
问题2
问题3
在双曲线的定义中,常数为什么要小于
环节二 问题探究 形成定义
不是,其轨迹是双曲线的一支.
在双曲线的定义中,若去掉“绝对值”,其轨迹还是双曲线吗?
问题2
结论
观看动态演示
退出
环节二 问题探究 形成定义
当常数等于零时,即
在双曲线的定义中,若去掉“非零”,其轨迹还是双曲线吗?
问题3
这时,动点的轨迹为线段的垂直平分线.
环节二 问题探究 形成定义
①如果定义中常数改为等于,此时动点的轨迹是以 为端点的两条射线(包括端点).
在双曲线的定义中,常数为什么要小于
问题4
②如果定义中常数改为大于 ,此时动点的轨迹不存在.
环节二 问题探究 形成定义
双曲线的定义
一般地,我们把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
回顾椭圆的标准方程的推导步骤及方法,能否类比推导双曲线的标准方程?
问题5
双曲线
环节三 探究运算 建立方程
观察双曲线的形状,如何建立适当的平面直角坐标系?
追问
01
环节三 探究运算 建立方程
如何用坐标表示双曲线上的点所满足的几何条件?
追问
02
双曲线的焦距为,
环节三 探究运算 建立方程
设是双曲线上任意一点,
则焦点的坐标分别为
如何写出曲线上的点所满足条件的集合?
追问
03
设 (为大于的常数,).
由双曲线的定义,双曲线就是下列点的集合:
环节三 探究运算 建立方程
根据点的坐标满足条件的集合写出方程.
因为 ,
类比椭圆标准方程的化简过程,化简①
所以 ①
环节三 探究运算 建立方程
将方程①左边的一个根式移到右边,得
对上式两边平方,得
整理,得
对上式两边平方,整理得
两边同时除以,得
环节三 探究运算 建立方程
由双曲线的定义知,,即,所以.
类比椭圆标准方程的建立过程,令 ,其中 ,代入上式,得
②
我们称方程②是双曲线的方程,这个方程叫做双曲线的标准方程. 它表示焦点在轴上,焦点分别是的双曲线,这里.
环节三 探究运算 建立方程
类比椭圆,焦点在轴上的双曲线的标准方程是什么?
问题6
双曲线的焦距为,焦点分别是,的意义同上,这时双曲线的方程是
这个方程也是双曲线的标准方程.
环节三 探究运算 建立方程
双曲线中的关系与椭圆中的关系有何不同?
问题7
双曲线标准方程中:,其中
与的大小关系不确定;
椭圆标准方程中,,其中,
环节三 探究运算 建立方程
观察双曲线的两种标准方程如何判断焦点所在的坐标轴?
问题8
谁的系数为正,焦点落在哪条轴上,分母为,反之亦然.
环节三 探究运算 建立方程
椭圆、双曲线标准方程的比较
椭圆及其标准方程 双曲线及其标准方程
定义式
abc的关系
焦点在轴上
焦点在轴上
椭圆、双曲线标准方程的比较
椭圆及其标准方程 双曲线及其标准方程
定义式
abc的关系
焦点在轴上
焦点在轴上
环节四 例题练习 巩固理解
例
已知双曲线的两个焦点分别为,双曲线上一点与, 的距离差的绝对值等于,求双曲线的标准方程.
解:
由于双曲线的焦点在轴上,所以设它的标准方程为
由,,得,又,因此 .
所以,双曲线的标准方程为
跟踪练习
根据条件写出双曲线标准方程.
①焦点为
②焦点为,且经过点
环节四 例题练习 巩固理解
链接高考
(2021年新高考Ⅰ卷·第21题)
在平面直角坐标系中,已知点 ,点M的轨迹为C.
(1)求C的方程;
环节四 例题练习 巩固理解
环节五:课堂小结 思维导图
双曲线及其标准方程
双曲线的定义
双曲线的标准方程
双曲线标准方程的求法及应用
知识内容:
思想方法
待定系数法
分类讨论
数形结合思想
类比
核心素养
数学抽象
双曲线的定义.
逻辑推理
运用定义推导双曲线的标准方程.
数学运算
双曲线标准方程的求法.
环节五:课堂小结 思维导图
必 做 课本P127:1、2、5、7
探究作业: 课本P121探究
环节六:课后作业 巩固提升
感谢
T H A N K S !
下节,精彩继续……
