【核心考点集训】第三单元《长方体与正方体》课件(共26张PPT)人教版五年级下册
文档属性
| 名称 | 【核心考点集训】第三单元《长方体与正方体》课件(共26张PPT)人教版五年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1001.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 09:23:13 | ||
图片预览








文档简介
(共26张PPT)
人教版 数学 五年级 下册
长方体与正方体
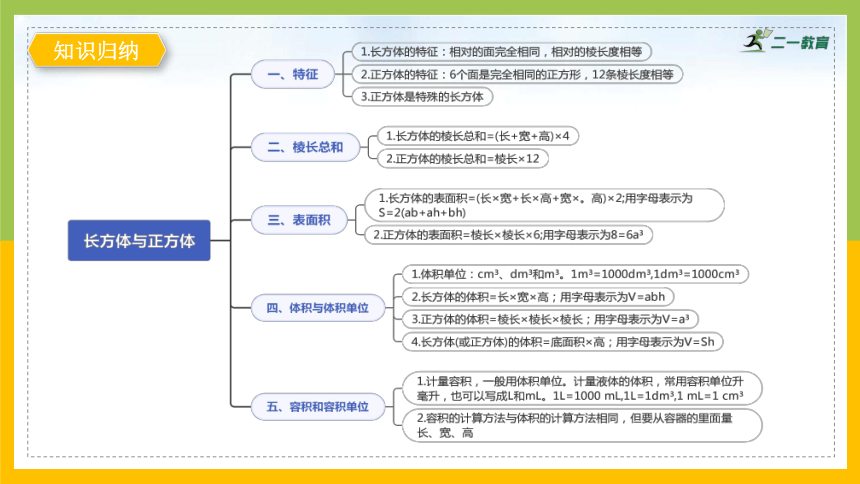
知识归纳
模块一:知识点复习
知识点一:长方体和正方体的认识
知识梳理
1.长方体的认识:
(1)长方体一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。围成长方体的长方形叫作面,面和面相交的线段叫作棱,棱和棱的交点叫作顶点。一个长方体有6个面、8个顶点和12条棱。相对的面完全相同,相对的棱长度相等。相交于同一顶点的三条棱的长度分别叫作长方体的长、宽、高。长方体的12条棱中有4条长、4条宽、4条高。
(2)长方体的棱长总和=(长+宽+高)×4。
知识点一:长方体和正方体的认识
知识梳理
2.正方体的认识:
(1)正方体是由6个完全相同的正方形围成的立体图形。正方体有6个面、8个顶点和12条棱。6个面完全相同,12条棱的长度都相等。
(2)正方体的棱长总和=棱长×12。
3.长方体和正方体的关系:
正方体是长、宽、高都相等的长方体。正方体是特殊的长方体。
知识点二:长方体和正方体的表面积
知识梳理
1.长方体或正方体6个面的面积之和,叫作它的表面积。
2.长方体的表面积计算公式:
长方体的表面积=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2。
3.正方体的表面积计算公式:
正方体的表面积=棱长×棱长×6。
4.在实际生活中,经常会遇到不需要计算出长方体或正方体6个面的总面积的情况。这时需要根据具体情况明确应该计算哪几个面的面积和。
知识点三:体积和体积单位
知识梳理
1.物体所占空间的大小叫作物体的体积。
2.计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm 、dm 和m 。
3.(1)长方体的体积公式:长方体的体积=长×宽×高。用字母表示长方体的体积公式:V=abh。
(2)正方体的体积公式:正方体的体积=棱长×棱长×棱长。用字母表示正方体的体积公式:V=a·a·a,a·a·a也可以写作“a ”,读作“a的立方”,表示3个a相乘。正方体的体积计算公式一般写成V=a 。
4.长方体或正方体底面的面积叫作底面积。长方体(或正方体)的体积=底面积×高。如果用字母S表示底面积,前面的公式可以写成V=Sh。
知识点三:体积和体积单位
知识梳理
1.物体所占空间的大小叫作物体的体积。
2.计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm 、dm 和m 。
3.(1)长方体的体积公式:长方体的体积=长×宽×高。用字母表示长方体的体积公式:V=abh。
(2)正方体的体积公式:正方体的体积=棱长×棱长×棱长。用字母表示正方体的体积公式:V=a·a·a,a·a·a也可以写作“a ”,读作“a的立方”,表示3个a相乘。正方体的体积计算公式一般写成V=a 。
4.长方体或正方体底面的面积叫作底面积。长方体(或正方体)的体积=底面积×高。如果用字母S表示底面积,前面的公式可以写成V=Sh。
知识点四:体积单位间的进率
知识梳理
1.m 和dm 、dm 和cm 分别是相邻的两组体积单位,进率都是1000;
即1m =1000 dm ,1 dm =1000 cm 。
2.体积单位间的换算方法:把高级单位的名数换算成低级单位的名数,用高级单位的数乘进率;把低级单位的名数换算成高级单位的名数,用低级单位的数除以进率。
知识点五:容积和容积单位
知识梳理
1.像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
2.计量容积一般用体积单位。计量液体的体积(如水、油等),常用容积单位升和毫升;
也可以写成L和mL。1L=1000mL。
3.容积单位和体积单位之间的关系。
1L=1dm 1mL=1cm
4.长方体或正方体容器容积的计算方法,跟体积的计算方法相同,但要从容器里面量长、宽、高。
5.求不规则物体的体积:用排水法求体积时,要把不规则物体完全浸没在水中。
模块二:例题讲解
有一个正方体,六个面分别写着A、B、C、D、E、F,请根据下面三种不同的摆法推测A、B、C相对的面上的字母。A相对的面上的字母是( );B相对的面上的字母是( );C相对的面上的字母是( )。
【典例1】相对面问题
分析:观察三幅图发现,三幅图中都有字母C,运用排除法先推断出C的相对面,再依次确定B、A相对的面上的字母。
解答:先确定C,与C相邻的字母有:A、B、D、E;所以C对F。
与A相邻的字母有:B、C、E,且C与F相对。所以A对D
与B相邻的字母有:A、C、D,且C与F相对,A与D相对。所有B对E。
D
E
F
【典例2】不规则图形的表面积问题
分析:(1)几何体②从前面看到6个面,
同理前面的对面也有6个面,右面和左面
各有5个面,上面和下面各有5个面,所以
几何体②的表面共有“5+6+5”个面。
(2)要想把几何体②朴成一个大正方体,要按照长、宽、高里最长的棱来确定。
下面两个几何体都是由棱长1cm的小正方体搭成的。几何体①的表面积可以按如下框内的方法计算。几何体②的表面积是多少平方厘米 如果添加相同的小正方体,把几何体②补成一个大正方体,表面积至少是多少平方厘米
解答:1×1=1(cm )(5+6+5)×2=32(cm )3×3×6=54(cm )
答:②的表面积是32cm ;把②补成一个大正方体,表面积至少是54cm 。
【典例3】长(正)方体拼接后表面积变化问题
把4个棱长为5cm的正方体拼成一个长方体,表面积减少多少平方厘米
分析:4个相同的正方体可能拼成的长方体的所有情况如图所示。由图可以发现,减少的面积等于正方体拼接面的面积之和。
情况一:减少了6个面;
情况二:减少了8个面。
解答:情况一:5×5×6=150(cm )
情况二:5×5×8=200(cm )
答:表面积减少150cm 或200 cm 。
【典例4】长(正)方体挖去一部分后的表面积计算
一个长5 dm、宽3 dm、高2 dm的长方体,现从一个角挖去个棱长1 dm的小正方体。剩下部分的表面积是多少平方分米
分析:观察图形,挖去一个小正方体后,减少了小正方体的上面、前面、右面3个面,同时增加了下面、后面、左面3个面,因此从总体上看,表面积没有变化。
解答:(5×3+5×2+3×2)×2=62(dm )
【典例5】体积变化问题
分析:一个长方体的高增加后,上面和下面的面积没有变化,增加的面积就是侧面4个小长方形的面积和,4个小长方形的面积全部相等。原来的长方体的高增加3cm后变成正方体,说明原来长方体的长和宽相等。
一个长方体,如果高增加3cm,就变成一个正方体。这时表面积比原来增加84 cm 。原来长方体的体积是多少立方厘米
解答:84÷4÷3=7(cm)
7×7×(7-3)=196(cm )
答:原来长方体的体积是196 cm 。
【典例6】用抓不变量法解决实际问题
分析:长方体容器平放和竖放时,容器内水的体积不变。图1平放时,水的体积=长×宽×高;图2竖放时的底面积=16×10=160(cm ),水的体积不变,高=水的体积÷底面积
有一个完全封闭的长方体容器,内壁的长是20cm,宽是16 cm,高是10 cm(厚度忽略不计),平放时水面高7cm(如图1)。如果把这个容器竖起来放(如图2),水面高多少厘米
解答:20×16×7=2240(cm )
2240÷(16×10)=14(cm)
【典例7】长(正)方体拼切求体积
一个长14 dm、高6dm的长方体。如果按下图所示把它切成两个小长方体,那么表面积增加108 dm 。求原来长方体的体积。
分析:一个长方体切成两个小长方体,表面积增加了两个横截面的面积,即横截面面积=108÷2=54(dm )。大长方体的侧面积是54 dm ,长是14 dm,最后根据体积公式计算即可。
解答:108÷2=54(dm )
54×14=756(dm )
答:原来长方体的体积是756 dm 。
【典例8】有水溢出的浸没问题
分析:石头的体积=水面上升部分的体积+溢出的水的体积。水面上升部分可看作长1.5 dm、宽1.2 dm、高0.9-0.7=0.2(dm)的长方体,根据长方体体积公式计算出水面上升部分的体积,然后加上溢出的水的体积即可。
一个内部长1.5 dm、宽1.2 dm、高0.9 dm的长方体水箱,水面高度是0.7dm,将一块石头浸没在水中后,溢出了250mL水。这块石头的体积是多少立方分米
解答:250 mL=0.25L=0.25 dm
1.5×1.2×(0.9-0.7)+0.25=0.61(dm )
答:这块石头的体积是0.61 dm 。
【典例9】物体没有完全浸入且水没有溢出的问题
分析:将一个正方体铁块放入长方体水缸中,水没有溢出水缸,这时铁块正方形的底面与水缸长方形的底面合在一起,现在水缸中水的底面积就是长方体水缸的底面积减去正方体铁块的底面积,而水缸中水的体积没有变化,所以可先求出现在水的深度,即用水的体积除以现在水的底面积。求出水缸中现在水的深度后,再减去原来水的深度,就可求出水面上升了多少。
一个长6 dm、宽4 dm、高4.8 dm的长方体水缸,水深1.5 dm。在其中放入一个棱长3 dm的正方体铁块,铁块没有被淹没,且水没有溢出。这时长方体水缸的水面上升了多少分米
解答:6×4×1.5÷(6×4-3×3)=2.4(dm) 2.4-1.5=0.9(dm)
答:这时长方体水缸的水面上升了0.9dm。
模块三:完成变式训练
1.老师特制了4个完全相同的正方体,并将它们按图1的方式放置,分别旋转后放置如图2,则图2中4个正方体底面上的点数之和是( )。
16
2.下图是由多个棱长为1cm的小正方体堆成的几何体。该几何体的表面积是多少平方厘米 如果在这个几何体上添加相同的小正方体,补成一个长方体。那么这个长方体的表面积至少是多少平方厘米
解答:1×1=1(cm )
(12+4+9)×2=50(cm )
(5×2+5×3+2×3)×2=62(cm )
答:该几何体的表面积是50 cm ;这个长方体的表面积至少是62 cm 。
3.用两个长6cm、宽2cm、高4cm的长方体拼成一个大长方体,大长方体的表面积最大是多少平方厘米
解答:(6×4+6×2+4×2)×2×2=176(cm )
176-4×2×2=160(cm )
答:大长方体的表面积最大是160cm 。
4.如图,由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,现自上而下挖掉中间的3个小正方体。剩下部分的表面积是多少
解答:1×3=3(cm)
3×3×6-1×1×2+1×3×4=64(cm )
答:剩下部分的表面积是64 cm 。
5.一个长方体木块,从上部和下部分别截去高为3cm和2cm的长方体,变成一个正方体,表面积减少了120 cm 。原来长方体的体积是多少立方厘米
120÷4÷(3+2)=6(cm) 6×6×(6+3+2)=396(cm )
答:原来长方体的体积是396 cm 。
6.小华放学回家,看见桌上放着两个玻璃鱼缸,爸爸在留言条上写着:“小华,你回家后,把A鱼缸的水倒入B鱼缸一些,使两个鱼缸中的水一样深。”小华按留言倒水后,这两个鱼缸现在的水深是多少厘米
解答:方法一:20×50×24=24000(cm )
(20+40)×50=3000(cm ) 24000÷3000=8(cm)
方法二:24÷[(40÷20)+1]=8(cm)
7.一个长方体,前后两个面都是边长为4.5 cm的正方形(如图),切成四块后表面积增加了440.5 cm 。求原长方体的体积。
解答:(440.5-4.5×4.5×2)÷2×4.5=900(cm )
8.一个长方体容器,底面是边长8cm的正方形,高16 cm,往容器中倒入一定量的水,使水面距离容器口2cm。现把一块鹅卵石放入容器中,会有部分水溢出。当把鹅卵石取出后,水面下降5 cme溢出的水的体积是多少
解答:8×8×(5-2)=192(cm )
9.一个正方体容器,从里面量棱长为6 dm,里面装有2 dm深的水。将一个棱长为4 dm的正方体铁块放入水中,水深变为多少分米
解答:(4×4×4+6×6×2)÷(6×6)=(dm)
<4说明铁块没有完全浸入水中
水深:6×6×2÷(6×6-4×4)=3.6(dm)
人教版 数学 五年级 下册
长方体与正方体
知识归纳
模块一:知识点复习
知识点一:长方体和正方体的认识
知识梳理
1.长方体的认识:
(1)长方体一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。围成长方体的长方形叫作面,面和面相交的线段叫作棱,棱和棱的交点叫作顶点。一个长方体有6个面、8个顶点和12条棱。相对的面完全相同,相对的棱长度相等。相交于同一顶点的三条棱的长度分别叫作长方体的长、宽、高。长方体的12条棱中有4条长、4条宽、4条高。
(2)长方体的棱长总和=(长+宽+高)×4。
知识点一:长方体和正方体的认识
知识梳理
2.正方体的认识:
(1)正方体是由6个完全相同的正方形围成的立体图形。正方体有6个面、8个顶点和12条棱。6个面完全相同,12条棱的长度都相等。
(2)正方体的棱长总和=棱长×12。
3.长方体和正方体的关系:
正方体是长、宽、高都相等的长方体。正方体是特殊的长方体。
知识点二:长方体和正方体的表面积
知识梳理
1.长方体或正方体6个面的面积之和,叫作它的表面积。
2.长方体的表面积计算公式:
长方体的表面积=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2。
3.正方体的表面积计算公式:
正方体的表面积=棱长×棱长×6。
4.在实际生活中,经常会遇到不需要计算出长方体或正方体6个面的总面积的情况。这时需要根据具体情况明确应该计算哪几个面的面积和。
知识点三:体积和体积单位
知识梳理
1.物体所占空间的大小叫作物体的体积。
2.计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm 、dm 和m 。
3.(1)长方体的体积公式:长方体的体积=长×宽×高。用字母表示长方体的体积公式:V=abh。
(2)正方体的体积公式:正方体的体积=棱长×棱长×棱长。用字母表示正方体的体积公式:V=a·a·a,a·a·a也可以写作“a ”,读作“a的立方”,表示3个a相乘。正方体的体积计算公式一般写成V=a 。
4.长方体或正方体底面的面积叫作底面积。长方体(或正方体)的体积=底面积×高。如果用字母S表示底面积,前面的公式可以写成V=Sh。
知识点三:体积和体积单位
知识梳理
1.物体所占空间的大小叫作物体的体积。
2.计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm 、dm 和m 。
3.(1)长方体的体积公式:长方体的体积=长×宽×高。用字母表示长方体的体积公式:V=abh。
(2)正方体的体积公式:正方体的体积=棱长×棱长×棱长。用字母表示正方体的体积公式:V=a·a·a,a·a·a也可以写作“a ”,读作“a的立方”,表示3个a相乘。正方体的体积计算公式一般写成V=a 。
4.长方体或正方体底面的面积叫作底面积。长方体(或正方体)的体积=底面积×高。如果用字母S表示底面积,前面的公式可以写成V=Sh。
知识点四:体积单位间的进率
知识梳理
1.m 和dm 、dm 和cm 分别是相邻的两组体积单位,进率都是1000;
即1m =1000 dm ,1 dm =1000 cm 。
2.体积单位间的换算方法:把高级单位的名数换算成低级单位的名数,用高级单位的数乘进率;把低级单位的名数换算成高级单位的名数,用低级单位的数除以进率。
知识点五:容积和容积单位
知识梳理
1.像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
2.计量容积一般用体积单位。计量液体的体积(如水、油等),常用容积单位升和毫升;
也可以写成L和mL。1L=1000mL。
3.容积单位和体积单位之间的关系。
1L=1dm 1mL=1cm
4.长方体或正方体容器容积的计算方法,跟体积的计算方法相同,但要从容器里面量长、宽、高。
5.求不规则物体的体积:用排水法求体积时,要把不规则物体完全浸没在水中。
模块二:例题讲解
有一个正方体,六个面分别写着A、B、C、D、E、F,请根据下面三种不同的摆法推测A、B、C相对的面上的字母。A相对的面上的字母是( );B相对的面上的字母是( );C相对的面上的字母是( )。
【典例1】相对面问题
分析:观察三幅图发现,三幅图中都有字母C,运用排除法先推断出C的相对面,再依次确定B、A相对的面上的字母。
解答:先确定C,与C相邻的字母有:A、B、D、E;所以C对F。
与A相邻的字母有:B、C、E,且C与F相对。所以A对D
与B相邻的字母有:A、C、D,且C与F相对,A与D相对。所有B对E。
D
E
F
【典例2】不规则图形的表面积问题
分析:(1)几何体②从前面看到6个面,
同理前面的对面也有6个面,右面和左面
各有5个面,上面和下面各有5个面,所以
几何体②的表面共有“5+6+5”个面。
(2)要想把几何体②朴成一个大正方体,要按照长、宽、高里最长的棱来确定。
下面两个几何体都是由棱长1cm的小正方体搭成的。几何体①的表面积可以按如下框内的方法计算。几何体②的表面积是多少平方厘米 如果添加相同的小正方体,把几何体②补成一个大正方体,表面积至少是多少平方厘米
解答:1×1=1(cm )(5+6+5)×2=32(cm )3×3×6=54(cm )
答:②的表面积是32cm ;把②补成一个大正方体,表面积至少是54cm 。
【典例3】长(正)方体拼接后表面积变化问题
把4个棱长为5cm的正方体拼成一个长方体,表面积减少多少平方厘米
分析:4个相同的正方体可能拼成的长方体的所有情况如图所示。由图可以发现,减少的面积等于正方体拼接面的面积之和。
情况一:减少了6个面;
情况二:减少了8个面。
解答:情况一:5×5×6=150(cm )
情况二:5×5×8=200(cm )
答:表面积减少150cm 或200 cm 。
【典例4】长(正)方体挖去一部分后的表面积计算
一个长5 dm、宽3 dm、高2 dm的长方体,现从一个角挖去个棱长1 dm的小正方体。剩下部分的表面积是多少平方分米
分析:观察图形,挖去一个小正方体后,减少了小正方体的上面、前面、右面3个面,同时增加了下面、后面、左面3个面,因此从总体上看,表面积没有变化。
解答:(5×3+5×2+3×2)×2=62(dm )
【典例5】体积变化问题
分析:一个长方体的高增加后,上面和下面的面积没有变化,增加的面积就是侧面4个小长方形的面积和,4个小长方形的面积全部相等。原来的长方体的高增加3cm后变成正方体,说明原来长方体的长和宽相等。
一个长方体,如果高增加3cm,就变成一个正方体。这时表面积比原来增加84 cm 。原来长方体的体积是多少立方厘米
解答:84÷4÷3=7(cm)
7×7×(7-3)=196(cm )
答:原来长方体的体积是196 cm 。
【典例6】用抓不变量法解决实际问题
分析:长方体容器平放和竖放时,容器内水的体积不变。图1平放时,水的体积=长×宽×高;图2竖放时的底面积=16×10=160(cm ),水的体积不变,高=水的体积÷底面积
有一个完全封闭的长方体容器,内壁的长是20cm,宽是16 cm,高是10 cm(厚度忽略不计),平放时水面高7cm(如图1)。如果把这个容器竖起来放(如图2),水面高多少厘米
解答:20×16×7=2240(cm )
2240÷(16×10)=14(cm)
【典例7】长(正)方体拼切求体积
一个长14 dm、高6dm的长方体。如果按下图所示把它切成两个小长方体,那么表面积增加108 dm 。求原来长方体的体积。
分析:一个长方体切成两个小长方体,表面积增加了两个横截面的面积,即横截面面积=108÷2=54(dm )。大长方体的侧面积是54 dm ,长是14 dm,最后根据体积公式计算即可。
解答:108÷2=54(dm )
54×14=756(dm )
答:原来长方体的体积是756 dm 。
【典例8】有水溢出的浸没问题
分析:石头的体积=水面上升部分的体积+溢出的水的体积。水面上升部分可看作长1.5 dm、宽1.2 dm、高0.9-0.7=0.2(dm)的长方体,根据长方体体积公式计算出水面上升部分的体积,然后加上溢出的水的体积即可。
一个内部长1.5 dm、宽1.2 dm、高0.9 dm的长方体水箱,水面高度是0.7dm,将一块石头浸没在水中后,溢出了250mL水。这块石头的体积是多少立方分米
解答:250 mL=0.25L=0.25 dm
1.5×1.2×(0.9-0.7)+0.25=0.61(dm )
答:这块石头的体积是0.61 dm 。
【典例9】物体没有完全浸入且水没有溢出的问题
分析:将一个正方体铁块放入长方体水缸中,水没有溢出水缸,这时铁块正方形的底面与水缸长方形的底面合在一起,现在水缸中水的底面积就是长方体水缸的底面积减去正方体铁块的底面积,而水缸中水的体积没有变化,所以可先求出现在水的深度,即用水的体积除以现在水的底面积。求出水缸中现在水的深度后,再减去原来水的深度,就可求出水面上升了多少。
一个长6 dm、宽4 dm、高4.8 dm的长方体水缸,水深1.5 dm。在其中放入一个棱长3 dm的正方体铁块,铁块没有被淹没,且水没有溢出。这时长方体水缸的水面上升了多少分米
解答:6×4×1.5÷(6×4-3×3)=2.4(dm) 2.4-1.5=0.9(dm)
答:这时长方体水缸的水面上升了0.9dm。
模块三:完成变式训练
1.老师特制了4个完全相同的正方体,并将它们按图1的方式放置,分别旋转后放置如图2,则图2中4个正方体底面上的点数之和是( )。
16
2.下图是由多个棱长为1cm的小正方体堆成的几何体。该几何体的表面积是多少平方厘米 如果在这个几何体上添加相同的小正方体,补成一个长方体。那么这个长方体的表面积至少是多少平方厘米
解答:1×1=1(cm )
(12+4+9)×2=50(cm )
(5×2+5×3+2×3)×2=62(cm )
答:该几何体的表面积是50 cm ;这个长方体的表面积至少是62 cm 。
3.用两个长6cm、宽2cm、高4cm的长方体拼成一个大长方体,大长方体的表面积最大是多少平方厘米
解答:(6×4+6×2+4×2)×2×2=176(cm )
176-4×2×2=160(cm )
答:大长方体的表面积最大是160cm 。
4.如图,由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,现自上而下挖掉中间的3个小正方体。剩下部分的表面积是多少
解答:1×3=3(cm)
3×3×6-1×1×2+1×3×4=64(cm )
答:剩下部分的表面积是64 cm 。
5.一个长方体木块,从上部和下部分别截去高为3cm和2cm的长方体,变成一个正方体,表面积减少了120 cm 。原来长方体的体积是多少立方厘米
120÷4÷(3+2)=6(cm) 6×6×(6+3+2)=396(cm )
答:原来长方体的体积是396 cm 。
6.小华放学回家,看见桌上放着两个玻璃鱼缸,爸爸在留言条上写着:“小华,你回家后,把A鱼缸的水倒入B鱼缸一些,使两个鱼缸中的水一样深。”小华按留言倒水后,这两个鱼缸现在的水深是多少厘米
解答:方法一:20×50×24=24000(cm )
(20+40)×50=3000(cm ) 24000÷3000=8(cm)
方法二:24÷[(40÷20)+1]=8(cm)
7.一个长方体,前后两个面都是边长为4.5 cm的正方形(如图),切成四块后表面积增加了440.5 cm 。求原长方体的体积。
解答:(440.5-4.5×4.5×2)÷2×4.5=900(cm )
8.一个长方体容器,底面是边长8cm的正方形,高16 cm,往容器中倒入一定量的水,使水面距离容器口2cm。现把一块鹅卵石放入容器中,会有部分水溢出。当把鹅卵石取出后,水面下降5 cme溢出的水的体积是多少
解答:8×8×(5-2)=192(cm )
9.一个正方体容器,从里面量棱长为6 dm,里面装有2 dm深的水。将一个棱长为4 dm的正方体铁块放入水中,水深变为多少分米
解答:(4×4×4+6×6×2)÷(6×6)=(dm)
<4说明铁块没有完全浸入水中
水深:6×6×2÷(6×6-4×4)=3.6(dm)
