2025学年山西考生九年级数学锐角三角函数重难点突破(含答案)
文档属性
| 名称 | 2025学年山西考生九年级数学锐角三角函数重难点突破(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 13:14:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
山西考生专项九年级数学锐角三角函数重难点突破
一、选择题
1.(2024九上·东营月考)如图,四边形是的内接四边形,,,,,则的长为( )
A. B. C. D.2
2.(2024九下·朔州模拟)如图是一张圆心为O,半径为的圆形纸片,沿弦所在直线折叠,使得经过点O,将纸片展平后,作,则图中阴影部分的面积等于( )
A. B. C. D.
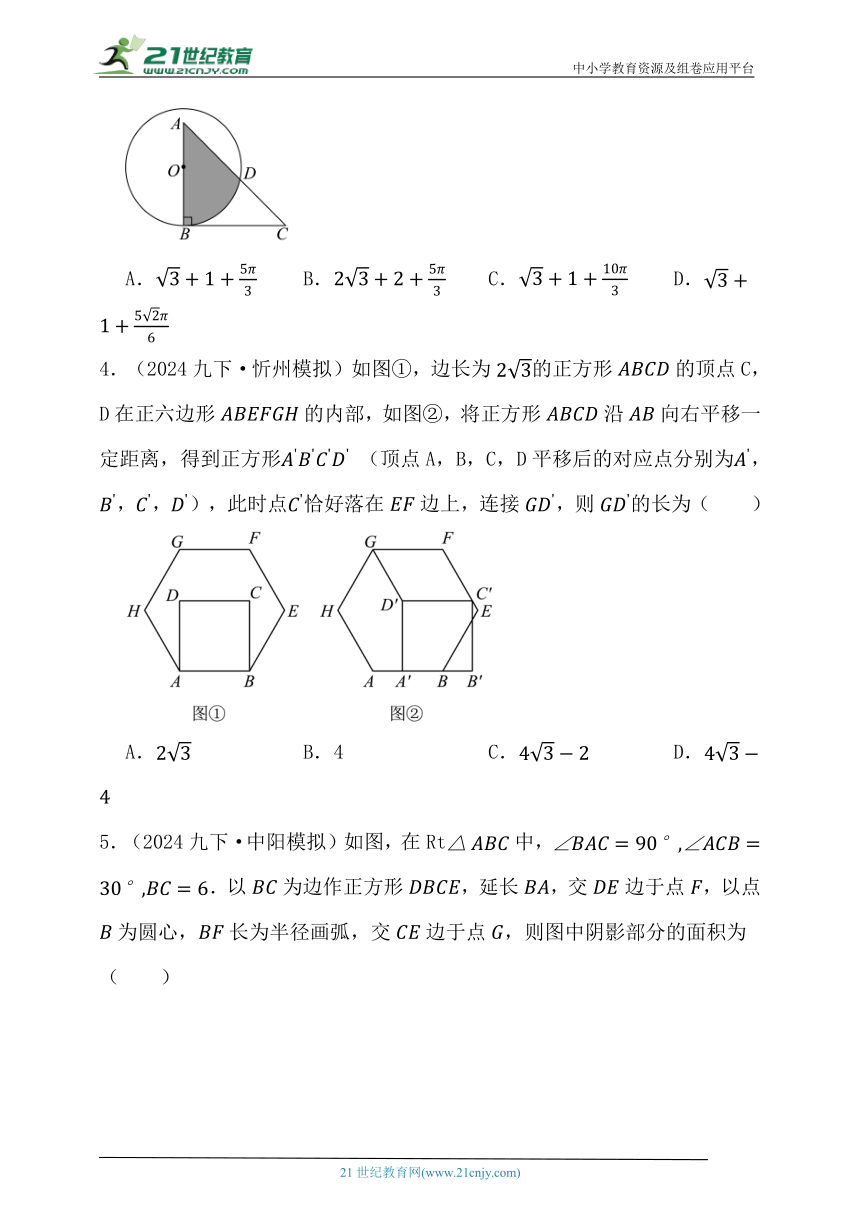
3.(2024九下·大同模拟)如图,将等腰直角三角形的直角顶点放在上,直角边经过圆心,斜边交于点,若,,则图中阴影部分的面积为( )
A. B. C. D.
4.(2024九下·忻州模拟)如图①,边长为的正方形的顶点C,D在正六边形的内部,如图②,将正方形沿向右平移一定距离,得到正方形 (顶点A,B,C,D平移后的对应点分别为,,,),此时点恰好落在边上,连接,则的长为( )
A. B.4 C. D.
5.(2024九下·中阳模拟)如图,在Rt中,.以为边作正方形,延长,交边于点,以点为圆心,长为半径画弧,交边于点,则图中阴影部分的面积为( )
A. B.
C. D.
二、填空题
6.(2024九下·南海月考)《海岛算经》是中国古代测量术的代表作,原名《重差》,这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义,如图,为测量海岛上一座山峰AH的高度,直立两根高1米的标杆和,两杆间距为3米,D,B,H三点共线,从点B处退行到点F,观察山顶A,发现A,C,F三点共线,且仰角为;从点D处退行到点G,观察山顶A,发现A,E,G三点共线,且仰角为(点F,G都在直线上).则山峰的高是 米(参考数据:,,)
7.(2024九下·运城模拟)如图,在中,,D是的中点,过点D作,垂足为E,M为上一点,点N在的延长线上,连接,交的延长线于点F,若,则的长为 .
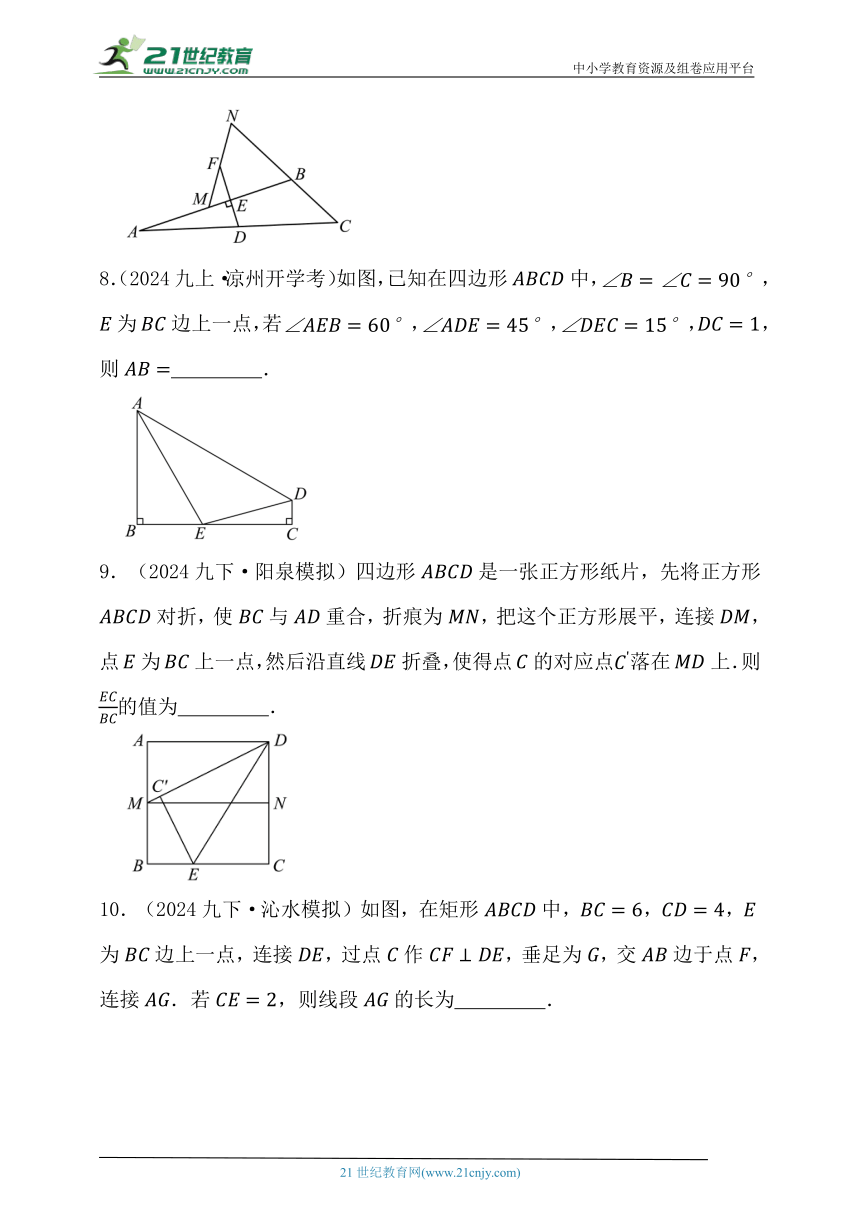
8.(2024九上·凉州开学考)如图,已知在四边形中,,为边上一点,若,,,,则 .
9.(2024九下·阳泉模拟)四边形是一张正方形纸片,先将正方形对折,使与重合,折痕为,把这个正方形展平,连接,点为上一点,然后沿直线折叠,使得点的对应点落在上.则的值为 .
10.(2024九下·沁水模拟)如图,在矩形中,,,为边上一点,连接,过点作,垂足为,交边于点,连接.若,则线段的长为 .
三、计算题
11.(2024九下·迎泽模拟)(1)计算:.
(2)解方程:.
12.(2024九下·平遥模拟)(1)计算:;
(2)解不等式组:,并确定此不等式组的整数解.
13.(2024九下·运城模拟)(1)计算:.
(2)下面是小颖同学解不等式的过程,请认真阅读并完成相应任务.
.
解:去分母,得……第一步
去括号,得.……第二步
移项,得.……第三步
合并同类项,得.……第四步
系数化为1,得.……第五步
任务:
任务一:填空:①上述解题过程中,第一步是依据______进行变形的;
②第______步开始出现错误,这一步错误的原因是______;
任务二:请直接写出该不等式的正确解集;
任务三:除了任务一中出现的错误外,请根据平时的学习经验,就解不等式时还需要注意的事项给其他同学提一条建议.
14.(2024九下·交城模拟)(1)计算:;
(2)解方程组:.
15.(2020九下·平定月考)
(1)计算:(-2015)0+|1- |-2cos45°+ +(- )-2.
(2)先化简,再求值:( - )÷ -1,其中x=-3.
四、综合题
16.(2025九上·澧县期末)随着城镇化建设的加快,高层建筑逐渐增多了,为防患于未然,更快更有效预防火灾,开辟新的救援通道,某城市消防中队新增添一台高空消防救援车.图1是高空救援消防车实物图,图2是其侧面示意图,点O,A,C在同一直线上,可绕着点O旋转,为云梯的液压杆,点O,B,D在同一水平线上,其中可伸缩,已知套管米,且套管的长度不变,现对高空救援消防车进行调试,测得,.
(1)求此时液压杆的长度;
(2)若消防人员在云梯末端工作台点C处高空救援时,将伸长到最大长度,云梯绕着点O逆时针旋转,即,过点作,垂足为G,过点C作,垂足为E,,垂足为H.如图3,测得铅直高度升高了3米(即),求伸长到的最大长度.(参考数据:,,,,,)
17.(2025九下·柳州开学考)如图1是某城建部门利用折臂升降机正在路边检修路灯的实物图片,图2是某时刻折臂升降机工作时的平面示意图,上折臂顶端恰好接触路灯杆,点A,B,C,D,E,F,M,N都在同一竖直平面内.路灯杆和折臂升降机的折臂底座都垂直于地面,且它们之间的水平距离,折臂底座,上折臂,上折臂与下折臂的夹角,下折臂与折臂底座的夹角,求上折臂顶端F到地面的距离.(结果精确到,参考数据:,,)
答案解析部分
1.【答案】C
【知识点】圆内接四边形的性质;求特殊角的三角函数值
2.【答案】A
【知识点】垂径定理;扇形面积的计算;翻折变换(折叠问题);解直角三角形
3.【答案】A
【知识点】等腰三角形的判定与性质;扇形面积的计算;解直角三角形
4.【答案】D
【知识点】多边形内角与外角;正方形的性质;平移的性质;锐角三角函数的定义
5.【答案】A
【知识点】扇形面积的计算;解直角三角形
6.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
7.【答案】
【知识点】解直角三角形;三角形的中位线定理
8.【答案】
【知识点】角平分线的性质;含30°角的直角三角形;勾股定理;解直角三角形
9.【答案】
【知识点】勾股定理;正方形的性质;解直角三角形
10.【答案】
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质;同角三角函数的关系
11.【答案】(1);(2).
【知识点】解分式方程;求特殊角的三角函数值
12.【答案】(1);(2)
【知识点】负整数指数幂;解一元一次不等式组;求特殊角的三角函数值
13.【答案】(1);(2)①不等式的两边都乘(或除以)同一个正数,不等号的方向不变;②二;去括号时,括号前面是“-”,去掉括号后括号内的第二项没有变号;;注意去分母时不要漏乘不含分母的项
【知识点】负整数指数幂;解一元一次不等式;求特殊角的三角函数值
14.【答案】(1)(2)
【知识点】负整数指数幂;求特殊角的三角函数值;代入消元法解二元一次方程组
15.【答案】(1)解:原式=1-(1- )-2× +2 +9
=1-1+ - +2 +9
=2 +9.
(2)解:原式=[ - ]÷ -1
= ÷ -1
= ÷ -1
= -1
=- ,
将x=-3代入,得:
原式=1.
【知识点】分式的化简求值;零指数幂;负整数指数幂;求特殊角的三角函数值
【解析】【分析】(1)根据零指数幂,绝对值,特殊角的锐角三角函数值,负整数指数幂进行计算求解即可;
(2)先化简得到 - ,再将 x=-3 代入计算求解即可。
16.【答案】(1)3米
(2)伸长到的最大长度为6米
【知识点】解直角三角形的其他实际应用;旋转的性质
17.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
试题分析部分
1、试卷总体分布分析
总分:45分
分值分布 客观题(占比) 10.0(22.2%)
主观题(占比) 35.0(77.8%)
题量分布 客观题(占比) 5(29.4%)
主观题(占比) 12(70.6%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
选择题 5(29.4%) 10.0(22.2%)
填空题 5(29.4%) 10.0(22.2%)
计算题 5(29.4%) 20.0(44.4%)
综合题 2(11.8%) 5.0(11.1%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (88.2%)
2 容易 (11.8%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 解直角三角形的实际应用﹣仰角俯角问题 7.0(15.6%) 6,17
2 含30°角的直角三角形 2.0(4.4%) 8
3 三角形的中位线定理 2.0(4.4%) 7
4 解一元一次不等式组 5.0(11.1%) 12
5 圆内接四边形的性质 2.0(4.4%) 1
6 矩形的性质 2.0(4.4%) 10
7 解直角三角形的其他实际应用 0.0(0.0%) 16
8 平移的性质 2.0(4.4%) 4
9 解直角三角形 12.0(26.7%) 2,3,5,7,8,9
10 多边形内角与外角 2.0(4.4%) 4
11 解分式方程 5.0(11.1%) 11
12 垂径定理 2.0(4.4%) 2
13 角平分线的性质 2.0(4.4%) 8
14 翻折变换(折叠问题) 2.0(4.4%) 2
15 相似三角形的判定与性质 2.0(4.4%) 10
16 同角三角函数的关系 2.0(4.4%) 10
17 负整数指数幂 15.0(33.3%) 12,13,14,15
18 等腰三角形的判定与性质 2.0(4.4%) 3
19 勾股定理 6.0(13.3%) 8,9,10
20 解一元一次不等式 5.0(11.1%) 13
21 分式的化简求值 0.0(0.0%) 15
22 旋转的性质 0.0(0.0%) 16
23 代入消元法解二元一次方程组 5.0(11.1%) 14
24 正方形的性质 4.0(8.9%) 4,9
25 求特殊角的三角函数值 22.0(48.9%) 1,11,12,13,14,15
26 扇形面积的计算 6.0(13.3%) 2,3,5
27 零指数幂 0.0(0.0%) 15
28 锐角三角函数的定义 2.0(4.4%) 4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
山西考生专项九年级数学锐角三角函数重难点突破
一、选择题
1.(2024九上·东营月考)如图,四边形是的内接四边形,,,,,则的长为( )
A. B. C. D.2
2.(2024九下·朔州模拟)如图是一张圆心为O,半径为的圆形纸片,沿弦所在直线折叠,使得经过点O,将纸片展平后,作,则图中阴影部分的面积等于( )
A. B. C. D.
3.(2024九下·大同模拟)如图,将等腰直角三角形的直角顶点放在上,直角边经过圆心,斜边交于点,若,,则图中阴影部分的面积为( )
A. B. C. D.
4.(2024九下·忻州模拟)如图①,边长为的正方形的顶点C,D在正六边形的内部,如图②,将正方形沿向右平移一定距离,得到正方形 (顶点A,B,C,D平移后的对应点分别为,,,),此时点恰好落在边上,连接,则的长为( )
A. B.4 C. D.
5.(2024九下·中阳模拟)如图,在Rt中,.以为边作正方形,延长,交边于点,以点为圆心,长为半径画弧,交边于点,则图中阴影部分的面积为( )
A. B.
C. D.
二、填空题
6.(2024九下·南海月考)《海岛算经》是中国古代测量术的代表作,原名《重差》,这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义,如图,为测量海岛上一座山峰AH的高度,直立两根高1米的标杆和,两杆间距为3米,D,B,H三点共线,从点B处退行到点F,观察山顶A,发现A,C,F三点共线,且仰角为;从点D处退行到点G,观察山顶A,发现A,E,G三点共线,且仰角为(点F,G都在直线上).则山峰的高是 米(参考数据:,,)
7.(2024九下·运城模拟)如图,在中,,D是的中点,过点D作,垂足为E,M为上一点,点N在的延长线上,连接,交的延长线于点F,若,则的长为 .
8.(2024九上·凉州开学考)如图,已知在四边形中,,为边上一点,若,,,,则 .
9.(2024九下·阳泉模拟)四边形是一张正方形纸片,先将正方形对折,使与重合,折痕为,把这个正方形展平,连接,点为上一点,然后沿直线折叠,使得点的对应点落在上.则的值为 .
10.(2024九下·沁水模拟)如图,在矩形中,,,为边上一点,连接,过点作,垂足为,交边于点,连接.若,则线段的长为 .
三、计算题
11.(2024九下·迎泽模拟)(1)计算:.
(2)解方程:.
12.(2024九下·平遥模拟)(1)计算:;
(2)解不等式组:,并确定此不等式组的整数解.
13.(2024九下·运城模拟)(1)计算:.
(2)下面是小颖同学解不等式的过程,请认真阅读并完成相应任务.
.
解:去分母,得……第一步
去括号,得.……第二步
移项,得.……第三步
合并同类项,得.……第四步
系数化为1,得.……第五步
任务:
任务一:填空:①上述解题过程中,第一步是依据______进行变形的;
②第______步开始出现错误,这一步错误的原因是______;
任务二:请直接写出该不等式的正确解集;
任务三:除了任务一中出现的错误外,请根据平时的学习经验,就解不等式时还需要注意的事项给其他同学提一条建议.
14.(2024九下·交城模拟)(1)计算:;
(2)解方程组:.
15.(2020九下·平定月考)
(1)计算:(-2015)0+|1- |-2cos45°+ +(- )-2.
(2)先化简,再求值:( - )÷ -1,其中x=-3.
四、综合题
16.(2025九上·澧县期末)随着城镇化建设的加快,高层建筑逐渐增多了,为防患于未然,更快更有效预防火灾,开辟新的救援通道,某城市消防中队新增添一台高空消防救援车.图1是高空救援消防车实物图,图2是其侧面示意图,点O,A,C在同一直线上,可绕着点O旋转,为云梯的液压杆,点O,B,D在同一水平线上,其中可伸缩,已知套管米,且套管的长度不变,现对高空救援消防车进行调试,测得,.
(1)求此时液压杆的长度;
(2)若消防人员在云梯末端工作台点C处高空救援时,将伸长到最大长度,云梯绕着点O逆时针旋转,即,过点作,垂足为G,过点C作,垂足为E,,垂足为H.如图3,测得铅直高度升高了3米(即),求伸长到的最大长度.(参考数据:,,,,,)
17.(2025九下·柳州开学考)如图1是某城建部门利用折臂升降机正在路边检修路灯的实物图片,图2是某时刻折臂升降机工作时的平面示意图,上折臂顶端恰好接触路灯杆,点A,B,C,D,E,F,M,N都在同一竖直平面内.路灯杆和折臂升降机的折臂底座都垂直于地面,且它们之间的水平距离,折臂底座,上折臂,上折臂与下折臂的夹角,下折臂与折臂底座的夹角,求上折臂顶端F到地面的距离.(结果精确到,参考数据:,,)
答案解析部分
1.【答案】C
【知识点】圆内接四边形的性质;求特殊角的三角函数值
2.【答案】A
【知识点】垂径定理;扇形面积的计算;翻折变换(折叠问题);解直角三角形
3.【答案】A
【知识点】等腰三角形的判定与性质;扇形面积的计算;解直角三角形
4.【答案】D
【知识点】多边形内角与外角;正方形的性质;平移的性质;锐角三角函数的定义
5.【答案】A
【知识点】扇形面积的计算;解直角三角形
6.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
7.【答案】
【知识点】解直角三角形;三角形的中位线定理
8.【答案】
【知识点】角平分线的性质;含30°角的直角三角形;勾股定理;解直角三角形
9.【答案】
【知识点】勾股定理;正方形的性质;解直角三角形
10.【答案】
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质;同角三角函数的关系
11.【答案】(1);(2).
【知识点】解分式方程;求特殊角的三角函数值
12.【答案】(1);(2)
【知识点】负整数指数幂;解一元一次不等式组;求特殊角的三角函数值
13.【答案】(1);(2)①不等式的两边都乘(或除以)同一个正数,不等号的方向不变;②二;去括号时,括号前面是“-”,去掉括号后括号内的第二项没有变号;;注意去分母时不要漏乘不含分母的项
【知识点】负整数指数幂;解一元一次不等式;求特殊角的三角函数值
14.【答案】(1)(2)
【知识点】负整数指数幂;求特殊角的三角函数值;代入消元法解二元一次方程组
15.【答案】(1)解:原式=1-(1- )-2× +2 +9
=1-1+ - +2 +9
=2 +9.
(2)解:原式=[ - ]÷ -1
= ÷ -1
= ÷ -1
= -1
=- ,
将x=-3代入,得:
原式=1.
【知识点】分式的化简求值;零指数幂;负整数指数幂;求特殊角的三角函数值
【解析】【分析】(1)根据零指数幂,绝对值,特殊角的锐角三角函数值,负整数指数幂进行计算求解即可;
(2)先化简得到 - ,再将 x=-3 代入计算求解即可。
16.【答案】(1)3米
(2)伸长到的最大长度为6米
【知识点】解直角三角形的其他实际应用;旋转的性质
17.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
试题分析部分
1、试卷总体分布分析
总分:45分
分值分布 客观题(占比) 10.0(22.2%)
主观题(占比) 35.0(77.8%)
题量分布 客观题(占比) 5(29.4%)
主观题(占比) 12(70.6%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
选择题 5(29.4%) 10.0(22.2%)
填空题 5(29.4%) 10.0(22.2%)
计算题 5(29.4%) 20.0(44.4%)
综合题 2(11.8%) 5.0(11.1%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (88.2%)
2 容易 (11.8%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 解直角三角形的实际应用﹣仰角俯角问题 7.0(15.6%) 6,17
2 含30°角的直角三角形 2.0(4.4%) 8
3 三角形的中位线定理 2.0(4.4%) 7
4 解一元一次不等式组 5.0(11.1%) 12
5 圆内接四边形的性质 2.0(4.4%) 1
6 矩形的性质 2.0(4.4%) 10
7 解直角三角形的其他实际应用 0.0(0.0%) 16
8 平移的性质 2.0(4.4%) 4
9 解直角三角形 12.0(26.7%) 2,3,5,7,8,9
10 多边形内角与外角 2.0(4.4%) 4
11 解分式方程 5.0(11.1%) 11
12 垂径定理 2.0(4.4%) 2
13 角平分线的性质 2.0(4.4%) 8
14 翻折变换(折叠问题) 2.0(4.4%) 2
15 相似三角形的判定与性质 2.0(4.4%) 10
16 同角三角函数的关系 2.0(4.4%) 10
17 负整数指数幂 15.0(33.3%) 12,13,14,15
18 等腰三角形的判定与性质 2.0(4.4%) 3
19 勾股定理 6.0(13.3%) 8,9,10
20 解一元一次不等式 5.0(11.1%) 13
21 分式的化简求值 0.0(0.0%) 15
22 旋转的性质 0.0(0.0%) 16
23 代入消元法解二元一次方程组 5.0(11.1%) 14
24 正方形的性质 4.0(8.9%) 4,9
25 求特殊角的三角函数值 22.0(48.9%) 1,11,12,13,14,15
26 扇形面积的计算 6.0(13.3%) 2,3,5
27 零指数幂 0.0(0.0%) 15
28 锐角三角函数的定义 2.0(4.4%) 4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
