第1-5单元应用题专项训练(含解析)-2024-2025学年数学五年级下册苏教版
文档属性
| 名称 | 第1-5单元应用题专项训练(含解析)-2024-2025学年数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 649.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 14:39:47 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第1-5单元应用题专项训练-2024-2025学年数学五年级下册苏教版
1.松树和柏树一共有750棵,柏树的棵数是松树的1.5倍,两种树各有多少棵?(用方程解答)
2.城建工人铺一条1320米长的自来水管道,铺了5天后,还剩280米没有铺。平均每天铺多少米?(用方程解答)
3.一辆客车和一辆货车分别从、甲、乙两地同时出发,相向而行,经过6小时相遇。客车每小时行75千米,货车每小时行60千米,甲、乙两地相距多少千米?(用方程解答)
4.一条高架路已经修了28.6千米,比剩下的4倍多5.8千米。这条高架路还剩多少千米没有修?
5.今年小明和爸爸的年龄加起来是53岁,爸爸的年龄比小明的3倍还大1岁。今年小明多少岁?
6.某停车场一共有260个车位,分为普通车位和充电桩车位,其中普通车位的数量是充电桩车位的5.5倍,该停车场普通车位和充电桩车位各有多少个?(方程解答)
7.小李买苹果用去7.4元,比买2千克橘子多用0.6元。每千克橘子多少元?(列方程解答)
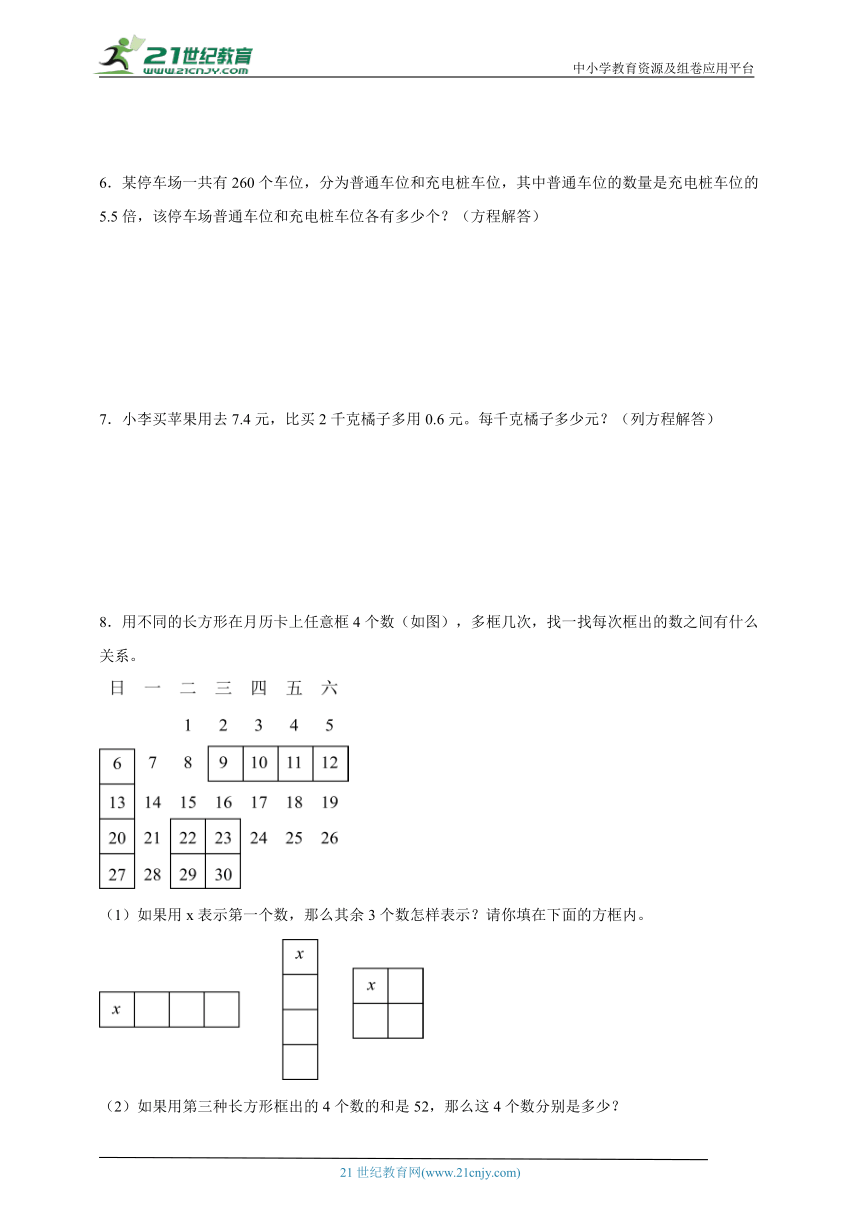
8.用不同的长方形在月历卡上任意框4个数(如图),多框几次,找一找每次框出的数之间有什么关系。
(1)如果用x表示第一个数,那么其余3个数怎样表示?请你填在下面的方框内。
(2)如果用第三种长方形框出的4个数的和是52,那么这4个数分别是多少?
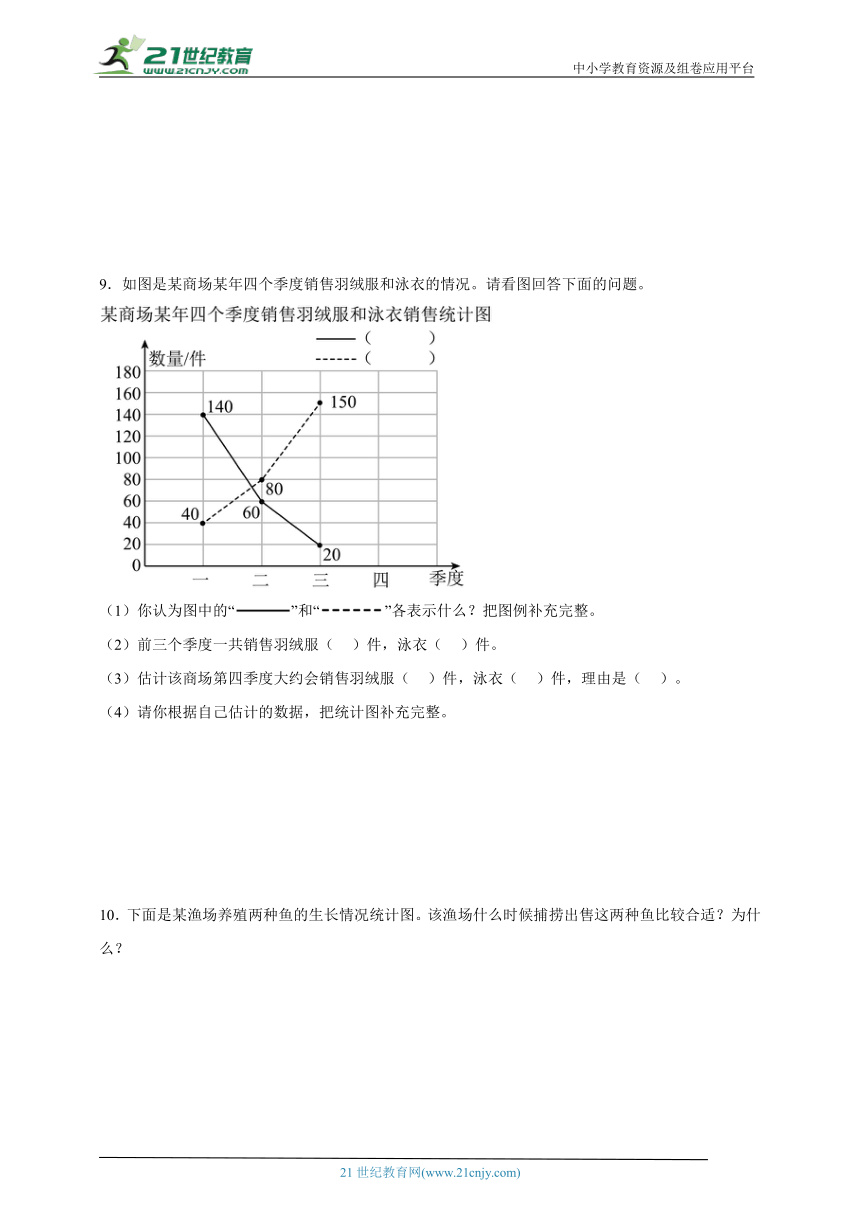
9.如图是某商场某年四个季度销售羽绒服和泳衣的情况。请看图回答下面的问题。
(1)你认为图中的“”和“”各表示什么?把图例补充完整。
(2)前三个季度一共销售羽绒服( )件,泳衣( )件。
(3)估计该商场第四季度大约会销售羽绒服( )件,泳衣( )件,理由是( )。
(4)请你根据自己估计的数据,把统计图补充完整。
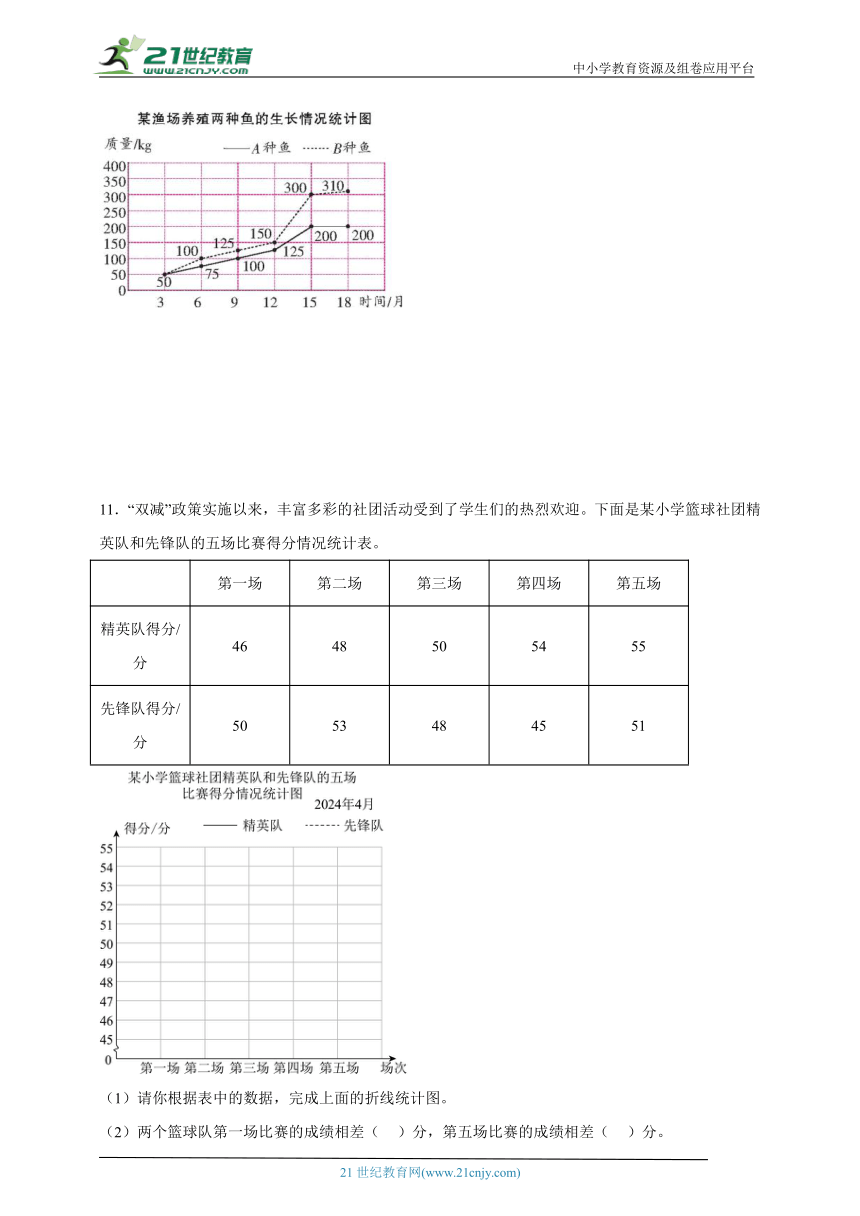
10.下面是某渔场养殖两种鱼的生长情况统计图。该渔场什么时候捕捞出售这两种鱼比较合适?为什么?
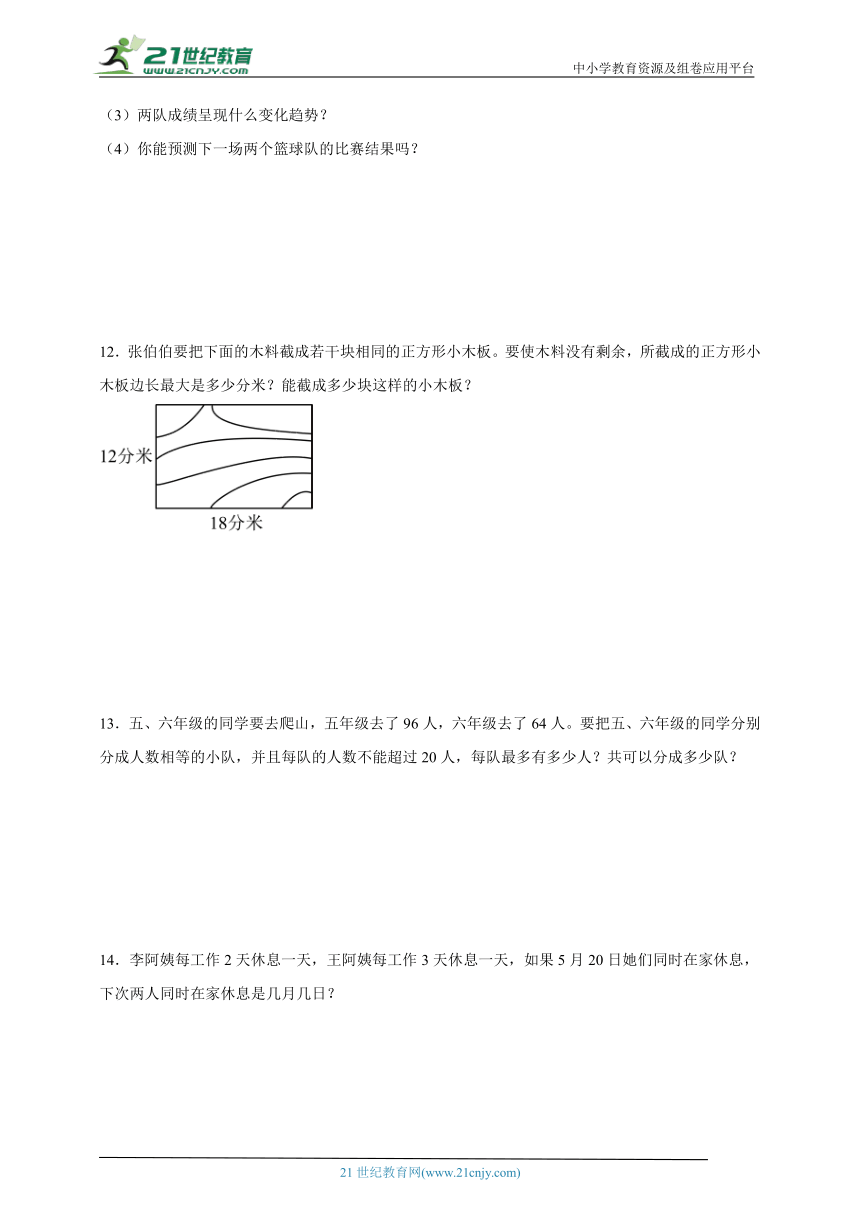
11.“双减”政策实施以来,丰富多彩的社团活动受到了学生们的热烈欢迎。下面是某小学篮球社团精英队和先锋队的五场比赛得分情况统计表。
第一场 第二场 第三场 第四场 第五场
精英队得分/分 46 48 50 54 55
先锋队得分/分 50 53 48 45 51
(1)请你根据表中的数据,完成上面的折线统计图。
(2)两个篮球队第一场比赛的成绩相差( )分,第五场比赛的成绩相差( )分。
(3)两队成绩呈现什么变化趋势?
(4)你能预测下一场两个篮球队的比赛结果吗?
12.张伯伯要把下面的木料截成若干块相同的正方形小木板。要使木料没有剩余,所截成的正方形小木板边长最大是多少分米?能截成多少块这样的小木板?
13.五、六年级的同学要去爬山,五年级去了96人,六年级去了64人。要把五、六年级的同学分别分成人数相等的小队,并且每队的人数不能超过20人,每队最多有多少人?共可以分成多少队?
14.李阿姨每工作2天休息一天,王阿姨每工作3天休息一天,如果5月20日她们同时在家休息,下次两人同时在家休息是几月几日?
15.学校体操队有36名男生和24名女生。
(1)如果男、女生分别排队,要使每排人数相同,每排最多排多少人?
(2)按上面的排法,男、女生各要排成几排?
16.学校图书馆买来5箱图书,一共300本,平均分给12个班,每班分到多少本?每班分到几分之几箱?每班分得这些图书的几分之几?
17.一个分数的分母比分子多12,把它约分后得。这个分数是多少?
18.在学校组织的足球射门比赛中,五(1)班三名运动员射门情况如下表。
姓名 李阳 刘明 张扬
射门次数 5 7 9
射中次数 3 4 5
射中次数占射门次数的几分之几
19.一个分数的分母是分子的6倍,这个分数写成最简分数是多少?如果分子与分母相差20,这个分数是多少?
20.李大爷收了吨西瓜,第一天卖出吨,第二天卖出吨。还剩多少吨?
21.食堂第一周用去吨大米,比第二周多用吨。两周一共用去多少吨大米?
22.暑假学校组织老师去旅游,去北京的占总人数的,去海南岛的占总人数的,其余的去黄山。去黄山旅游的占总人数的几分之几?
23.一个等腰三角形两条边的长分别是分米和分米。这个等腰三角形的周长是多少分米?
24.小宇爱好航天,课余时间他收集了三种飞船图片。其中收集的“神舟十五号”飞船图片占总数的,“天舟六号”飞船图片比“神舟十五号”飞船图片少占总数的,剩下的是“神舟十六号”飞船图片。他收集的“天舟六号”和“神舟十五号”飞船图片的数量占总数的几分之几?
《第1-5单元应用题专项训练-2024-2025学年数学五年级下册苏教版》参考答案
1.300棵;450棵
【分析】设松树有x棵,则柏树有1.5x棵,根据松树棵数+柏树棵数=总棵数,列出方程求出x的值是松树棵数,松树棵数×1.5=柏树棵数。
【详解】解:设松树有x棵,则柏树有1.5x棵。
x+1.5x=750
2.5x=750
2.5x÷2.5=750÷2.5
x=300
300×1.5=450(棵)
答:松树有300棵,柏树有450棵。
2.208米
【分析】根据题意可得出等量关系:平均每天铺的长度×铺的天数+还剩的长度=自来水管道的全长,据此列出方程,并求解。
【详解】解:设平均每天铺米。
5+280=1320
5+280-280=1320-280
5=1040
5÷5=1040÷5
=208
答:平均每天铺208米。
3.810千米
【分析】路程和÷相遇时间=速度和,设甲、乙两地相距x千米,根据速度和-客车速度=货车速度,列出方程解答即可。
【详解】解:设甲、乙两地相距x千米。
x÷6-75=60
x÷6-75+75=60+75
x÷6=135
x÷6×6=135×6
x=810
答:甲、乙两地相距810千米。
4.5.7千米
【分析】设这条高架路还剩x千米。已经修的长度比剩下的4倍多5.8千米,即剩下的长度×4+5.8千米=已经修的长度,列方程:4x+5.8=28.6,解方程,即可解答。
【详解】解:设这条高架路还剩x千米。
4x+5.8=28.6
4x+5.8-5.8=28.6-5.8
4x=22.8
4x÷4=22.8÷4
x=5.7
答:这条高架还剩5.7千米。
5.13岁
【分析】设今年小明x岁,爸爸的年龄比小明的3倍还大1岁,则爸爸年级是(3x+1)岁;今年小明和爸爸的年龄加起来是53岁,即今年小明年龄+今年爸爸年龄=53岁,列方程:x+3x+1=53,解方程,即可解答。
【详解】解:设今年小明x岁,则今年爸爸是(3x+1)岁。
x+3x+1=53
4x+1=53
4x+1-1=53-1
4x=52
4x÷4=52÷4
x=13
答:今年小明13岁。
6.普通车位有220个;充电桩车位有40个
【分析】设该停车场充电桩车位有x个,则普通车位的数量是5.5x个,根据等量关系:“普通车位的数量+充电桩车位的数量=260个”列方程解答求出充电桩车位的个数,再乘5.5求出普通车位的个数。
【详解】解:设该停车场充电桩车位有x个。
x+5.5x=260
6.5x=260
6.5x÷6.5=260÷6.5
x=40
40×5.5=220(个)
答:该停车场普通车位有220个,充电桩车位有40个。
7.3.4元
【分析】设每千克橘子x元,2千克橘子是2x元;小李买苹果用去的钱数比买2千克橘子多用0.6元,即买苹果的钱数-买2千克橘子的钱数=0.6元,列方程:7.4-2x=0.6,解方程,即可解答。
【详解】解:设每千克橘子x元,2千克橘子是2x元。
7.4-2x=0.6
7.4-2x+2x-0.6=0.6-0.6+2x
2x=7.4-0.6
2x=6.8
2x÷2=6.8÷2
x=3.4
答:每千克橘子3.4元。
8.(1)见详解
(2)9、10、16、17
【分析】(1)在日历中按图中框出的四个日期是在同一行或者同一列,同一行连续的四个数从左到右依次相差1,同一列的四个数从上到下依次相差7,框出的“田”字形的四个数中,已知左上角的数,则右边的数要加1,下方的数加7,右下方的数加8,据此可得出答案。
(2)可设第三种方法框出的四个数中左上角的数为x,则右边的数为x+1,下方的数为x+7,右下角的数为x+8,四个数相加等于52,解出方程,进而得出四个数。
【详解】(1)第一个图形第一个数x,则右边的数依次为:x+1,x+2,x+3;第二个图形中第一个数是x,则下方的数依次为:x+7,x+14,x+21;第三个图形中左上角数x,则右上角数为x+1,左下角的数为x+7,右下角的数为x+8。如图:
(2)解:设长方形框中的左上角的数为x,则另外3个数分别为:x+1、x+7、x+8,可列出方程:
x+(x+1)+(x+7)+(x+8)=52
4x+16=52
4x+16-16=52-16
4x=36
4x÷4=36÷4
x=9,即另外三个数分别为:10、16、17。
答:这4个数分别是9、10、16、17。
9.(1)“”表示羽绒服的销售情况;“”表示泳衣的销售情况
(2)220;270
(3)100;80;见详解
(4)见详解
【分析】(1)从图中可知:第一季度(1、2、3月),温度低,羽绒服销量高,泳衣销量低;第三季度(7、8、9月),温度高,羽绒服销量低,泳衣销量高,据此判断即可。
(2)分别求出前三个季度羽绒服和泳衣的销量之和即可。
(3)根据第四季度(10、11、12月)天气转冷,泳衣的销售数量可能会下降,羽绒服数量可能会上升。
(4)根据数据,将统计图补充完整即可。
【详解】
(1)“”表示羽绒服的销售情况;“”表示泳衣的销售情况。
(2)140+60+20=220(件)
40+80+150=270(件)
前三个季度一共销售羽绒服220件,泳衣270件。
(3)估计该商场第四季度大约会销售羽绒服100件,泳衣80件,理由是:到第四季度已进入冬季,所以羽绒服的销售量要比第三季度有所上升,估计销售量是100件;而泳衣的销售量一定比第三季度下降,估计销售量为80件(合理即可,答案不唯一)
(4)如图:
10.见详解
【分析】观察统计图可以发现:在3个月到12个月这个范围内,两种鱼的生长都呈上升趋势,且变化幅度较小;在12个月到15个月这个范围内,两种鱼生长的上升度都较大,生长迅速;在15个月以后,A种鱼的生长速度非常缓慢,B种鱼停止生长,捕捞出售这两种鱼的最佳时间应该是这两种鱼快速生长期停止之后,这样既可以避免提前捕捞造成单尾鱼的质量过轻,又可以避免延时捕捞造成饲料的浪费,据此解答。
【详解】这个渔场在15个月~18个月时捕捞出售这两种鱼比较合适;因为此时鱼生长慢。
11.(1)折线统计图见详解
(2)4;4
(3)精英队的成绩呈逐渐上升趋势;先锋队的成绩呈先上升后下降,再上升的不稳定趋势。
(4)我预测下一场比赛精英队获胜。
【分析】(1)根据统计表中的数据,分别找到精英队和先锋队在每一场比赛中的得分,直接在统计图中找到对应的位置,标出各个数据点,用直线将同一队伍的数据点依次连接起来,就得到了折线统计图。
(2)找出第一场比赛时的成绩,用先锋队的得分减去精英队的得分;找出第五场比赛时的成绩,用精英队的得分减去先锋队的得分。
(3)根据折线统计图的变化趋势解答即可。从折线统计图可以看出,精英队的成绩整体呈现上升的趋势;先锋队的成绩呈现先上升(第一场到第二场),再下降(第二场到第四场),后上升(第四场到第五场)的变化趋势。
(4)根据折线统计图变化趋势直接解答即可。根据两队的历史成绩和变化趋势,可以预测下一场比赛精英队可能会获胜,因为他们的成绩整体呈上升趋势,表现更稳定。
【详解】(1)根据分析,画图如下:
(2)50-46=4(分),55-51=4(分)
两个篮球队第一场比赛的成绩相差4分,第五场比赛的成绩相差4分。
(3)根据分析,精英队的成绩呈逐渐上升趋势;先锋队的成绩呈先上升后下降,再上升的不稳定趋势。
(4)我预测下一场两个篮球队的比赛结果是:精英队获胜,因为他们的成绩比较稳定,且呈上升趋势。
12.6分米;6块
【分析】把一块长方形木料截成若干块相同的正方形小木板且没有剩余,说明正方形小木板的边长是长、宽的公因数,求正方形小木板的最长边长,就是求长、宽的最大公因数;用分解质因数的方法求出长、宽的最大公因数,再分别求出长、宽各可以截几个,最后相乘就是能截的块数。
【详解】18=2×3×3
12=2×2×3
18和12的最大公因数是:2×3=6
即正方形小木板边长最大是6分米。
18÷6=3(个)
12÷6=2(个)
一共:3×2=6(块)
答:所截成的正方形小木板边长最大是6分米,能截成6块这样的小木板。
13.16人;10队
【分析】找一个数的因数的方法:列乘法算式找因数,按照从小到大的顺序,一组一组的写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数;分别求出96和64的因数,再求出96和64的公因数,找出小于20的最大公因数,即就是每队的人数,再用五年级和六年级人数和除以每队人数,即可解答。
【详解】96=1×96=2×48=3×32=4×24=6×16=8×12
96的因数有:1,2,3,4,6,8,12,16,24,32,48,96。
64=1×64=2×32=4×16=8×8
64的因数有:1,2,4,8,16,32,64。
96和64的公因数有:1,2,4,8,16,32。
小于20的最大公因数是16;每队最多16人。
(96+64)÷16
=160÷16
=10(队)
答:每队最多16人,共可以分10队。
14.6月1日
【分析】根据题意,李阿姨每工作2天休息一天,即李阿姨每3天休息一天;王阿姨每工作3天休息一天,即王阿姨每4天休息一天;那么她们同时在家休息的间隔天数是3和4的公倍数;先求出3和4的最小公倍数,再加上上一次她们同时在家休息的日期,即可求出下次两人同时在家休息的日期。
【详解】2+1=3(天)
3+1=4(天)
3和4的最小公倍数是:3×4=12
即每12天两人同时在家休息。
5月20日+12天=6月1日
答:下次两人同时在家休息是6月1日。
15.(1)12人
(2)男生3排;女生2排
【分析】(1)要使每排人数相同,而且每排人数尽可能多,每排人数应是36和24的最大公因数,计算36和24的最大公因数即可解答。
(2)分别用男生的人数和女生的人数除以每排的人数,据此解答。
【详解】(1)36=2×2×3×3
24=2×2×2×3
36和24的最大公因数是2×2×3=12。
答:要使每排人数相同,每排最多排12人。
(2)男生:36÷12=3(排)
女生:24÷12=2(排)
答:按上面的排法,男生要排3排,女生要排2排。
16.25本;箱;
【分析】根据平均分用除法计算,第一问用总本数除以班数,第二问用总箱数除以班数,第三问把图书总数看作单位“1”,根据分数的意义,把1平均分成12份,每份是。
【详解】(本)
(箱)
答:每班分到25本,每班分到箱,每班分得这些图书的。
17.
【分析】根据题意,把一个分数约分后得,分母与分子多3;原来分数的分母比分子多12,说明约分时分数的分子和分母同时除以4;那么把约分后的分数的分子、分母同时乘4,即可求出原来的分数。
【详解】10-7=3
12÷3=4
=
答:这个分数是。
18.;;
李阳;过程见详解
【分析】先用每人射中次数除以射门次数,求出每人射中次数占射门次数的几分之几,据此填表;再根据分数大小比较的方法进行比较,得出谁射门最准。
分数大小的比较:
分母相同时,分子越大,分数值就越大;
分子相同时,分母越大,分数值反而越小;
分子、分母都不相同时,利用分数的基本性质化成同分母或同分子的分数进行比较。
【详解】李阳:3÷5=
刘明:4÷7=
张扬:5÷9=
填表如下:
姓名 李阳 刘明 张扬
射门次数 5 7 9
射中次数 3 4 5
射中次数占射门次数的几分之几
==
==
==
>>
即>>。
答:李阳射门最准。
19.;
【分析】分子和分母的公因数只有1的分数叫最简分数。如果一个最简分数的分母是分子的6倍,则分母是分子的倍数,但它们的公因数只有1,那么分数的分子是1,分母是6,据此写出分数;
分数的分母是分子的6倍,分子与分母相差20,根据差倍问题中“较小数=差÷(倍数-1)”,用20除以(6-1)即可求出分子,用分子乘6求出分母。
【详解】一个分数的分母是分子的6倍,这个分数写成最简分数是;
分子:20÷(6-1)
=20÷5
=4
分母:4×6=24
则这个分数是。
20.吨
【分析】用西瓜的总重量减去第一天卖出西瓜的重量,减去第二天卖出西瓜的重量,即可求出剩下的重量。
【详解】--
=--
=-
=(吨)
答:还剩吨。
21.吨
【分析】用第一周用去大米的重量-,求出第二周用去大米的重量,再把两周用去大米的重量相加,即可解答。
【详解】-+
=-+
=+
=(吨)
答:两周一共用去吨大米。
22.
【分析】把暑假出行去旅游的总人数看作单位“1”,用单位“1”分别减去去北京的占总人数的和去海南岛的占总人数的,所得差即为去黄山旅游的占总人数的几分之几。
【详解】
答:去黄山旅游的占总人数的。
23.分米
【分析】先要判断等腰三角形的腰和底的长各是多少分米,根据三角形的两边之和大于第三条边,两边之差小于第三条边求出另一条边的长度,最后求出三条边的长度之和就是这个等腰三角形的周长,据此解答。
【详解】①当分米为等腰三角形的腰时
(分米)
(分米)
因为,所以等腰三角形的三条边的长度分别是分米、分米和分米。
当分米为等腰三角形的腰时
(分米)
因为,所以分米、分米和分米不能组成三角形。
(分米)
答:这个等腰三角形的周长是分米。
24.
【分析】“天舟六号”飞船图片比“神舟十五号”飞船图片少占总数的,“神舟十五号”飞船图片占总数的分率=“天舟六号”飞船图片占总数的分率-,最后再加上“神舟十五号”飞船图片占总数的分率。
在分数的计算过程中,先同分母分数相加,然后异分母分数相加转化为同分母分数相加即可。
【详解】
=
答:他收集的“天舟六号”和“神舟十五号”飞船图片的数量占总数的。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-5单元应用题专项训练-2024-2025学年数学五年级下册苏教版
1.松树和柏树一共有750棵,柏树的棵数是松树的1.5倍,两种树各有多少棵?(用方程解答)
2.城建工人铺一条1320米长的自来水管道,铺了5天后,还剩280米没有铺。平均每天铺多少米?(用方程解答)
3.一辆客车和一辆货车分别从、甲、乙两地同时出发,相向而行,经过6小时相遇。客车每小时行75千米,货车每小时行60千米,甲、乙两地相距多少千米?(用方程解答)
4.一条高架路已经修了28.6千米,比剩下的4倍多5.8千米。这条高架路还剩多少千米没有修?
5.今年小明和爸爸的年龄加起来是53岁,爸爸的年龄比小明的3倍还大1岁。今年小明多少岁?
6.某停车场一共有260个车位,分为普通车位和充电桩车位,其中普通车位的数量是充电桩车位的5.5倍,该停车场普通车位和充电桩车位各有多少个?(方程解答)
7.小李买苹果用去7.4元,比买2千克橘子多用0.6元。每千克橘子多少元?(列方程解答)
8.用不同的长方形在月历卡上任意框4个数(如图),多框几次,找一找每次框出的数之间有什么关系。
(1)如果用x表示第一个数,那么其余3个数怎样表示?请你填在下面的方框内。
(2)如果用第三种长方形框出的4个数的和是52,那么这4个数分别是多少?
9.如图是某商场某年四个季度销售羽绒服和泳衣的情况。请看图回答下面的问题。
(1)你认为图中的“”和“”各表示什么?把图例补充完整。
(2)前三个季度一共销售羽绒服( )件,泳衣( )件。
(3)估计该商场第四季度大约会销售羽绒服( )件,泳衣( )件,理由是( )。
(4)请你根据自己估计的数据,把统计图补充完整。
10.下面是某渔场养殖两种鱼的生长情况统计图。该渔场什么时候捕捞出售这两种鱼比较合适?为什么?
11.“双减”政策实施以来,丰富多彩的社团活动受到了学生们的热烈欢迎。下面是某小学篮球社团精英队和先锋队的五场比赛得分情况统计表。
第一场 第二场 第三场 第四场 第五场
精英队得分/分 46 48 50 54 55
先锋队得分/分 50 53 48 45 51
(1)请你根据表中的数据,完成上面的折线统计图。
(2)两个篮球队第一场比赛的成绩相差( )分,第五场比赛的成绩相差( )分。
(3)两队成绩呈现什么变化趋势?
(4)你能预测下一场两个篮球队的比赛结果吗?
12.张伯伯要把下面的木料截成若干块相同的正方形小木板。要使木料没有剩余,所截成的正方形小木板边长最大是多少分米?能截成多少块这样的小木板?
13.五、六年级的同学要去爬山,五年级去了96人,六年级去了64人。要把五、六年级的同学分别分成人数相等的小队,并且每队的人数不能超过20人,每队最多有多少人?共可以分成多少队?
14.李阿姨每工作2天休息一天,王阿姨每工作3天休息一天,如果5月20日她们同时在家休息,下次两人同时在家休息是几月几日?
15.学校体操队有36名男生和24名女生。
(1)如果男、女生分别排队,要使每排人数相同,每排最多排多少人?
(2)按上面的排法,男、女生各要排成几排?
16.学校图书馆买来5箱图书,一共300本,平均分给12个班,每班分到多少本?每班分到几分之几箱?每班分得这些图书的几分之几?
17.一个分数的分母比分子多12,把它约分后得。这个分数是多少?
18.在学校组织的足球射门比赛中,五(1)班三名运动员射门情况如下表。
姓名 李阳 刘明 张扬
射门次数 5 7 9
射中次数 3 4 5
射中次数占射门次数的几分之几
19.一个分数的分母是分子的6倍,这个分数写成最简分数是多少?如果分子与分母相差20,这个分数是多少?
20.李大爷收了吨西瓜,第一天卖出吨,第二天卖出吨。还剩多少吨?
21.食堂第一周用去吨大米,比第二周多用吨。两周一共用去多少吨大米?
22.暑假学校组织老师去旅游,去北京的占总人数的,去海南岛的占总人数的,其余的去黄山。去黄山旅游的占总人数的几分之几?
23.一个等腰三角形两条边的长分别是分米和分米。这个等腰三角形的周长是多少分米?
24.小宇爱好航天,课余时间他收集了三种飞船图片。其中收集的“神舟十五号”飞船图片占总数的,“天舟六号”飞船图片比“神舟十五号”飞船图片少占总数的,剩下的是“神舟十六号”飞船图片。他收集的“天舟六号”和“神舟十五号”飞船图片的数量占总数的几分之几?
《第1-5单元应用题专项训练-2024-2025学年数学五年级下册苏教版》参考答案
1.300棵;450棵
【分析】设松树有x棵,则柏树有1.5x棵,根据松树棵数+柏树棵数=总棵数,列出方程求出x的值是松树棵数,松树棵数×1.5=柏树棵数。
【详解】解:设松树有x棵,则柏树有1.5x棵。
x+1.5x=750
2.5x=750
2.5x÷2.5=750÷2.5
x=300
300×1.5=450(棵)
答:松树有300棵,柏树有450棵。
2.208米
【分析】根据题意可得出等量关系:平均每天铺的长度×铺的天数+还剩的长度=自来水管道的全长,据此列出方程,并求解。
【详解】解:设平均每天铺米。
5+280=1320
5+280-280=1320-280
5=1040
5÷5=1040÷5
=208
答:平均每天铺208米。
3.810千米
【分析】路程和÷相遇时间=速度和,设甲、乙两地相距x千米,根据速度和-客车速度=货车速度,列出方程解答即可。
【详解】解:设甲、乙两地相距x千米。
x÷6-75=60
x÷6-75+75=60+75
x÷6=135
x÷6×6=135×6
x=810
答:甲、乙两地相距810千米。
4.5.7千米
【分析】设这条高架路还剩x千米。已经修的长度比剩下的4倍多5.8千米,即剩下的长度×4+5.8千米=已经修的长度,列方程:4x+5.8=28.6,解方程,即可解答。
【详解】解:设这条高架路还剩x千米。
4x+5.8=28.6
4x+5.8-5.8=28.6-5.8
4x=22.8
4x÷4=22.8÷4
x=5.7
答:这条高架还剩5.7千米。
5.13岁
【分析】设今年小明x岁,爸爸的年龄比小明的3倍还大1岁,则爸爸年级是(3x+1)岁;今年小明和爸爸的年龄加起来是53岁,即今年小明年龄+今年爸爸年龄=53岁,列方程:x+3x+1=53,解方程,即可解答。
【详解】解:设今年小明x岁,则今年爸爸是(3x+1)岁。
x+3x+1=53
4x+1=53
4x+1-1=53-1
4x=52
4x÷4=52÷4
x=13
答:今年小明13岁。
6.普通车位有220个;充电桩车位有40个
【分析】设该停车场充电桩车位有x个,则普通车位的数量是5.5x个,根据等量关系:“普通车位的数量+充电桩车位的数量=260个”列方程解答求出充电桩车位的个数,再乘5.5求出普通车位的个数。
【详解】解:设该停车场充电桩车位有x个。
x+5.5x=260
6.5x=260
6.5x÷6.5=260÷6.5
x=40
40×5.5=220(个)
答:该停车场普通车位有220个,充电桩车位有40个。
7.3.4元
【分析】设每千克橘子x元,2千克橘子是2x元;小李买苹果用去的钱数比买2千克橘子多用0.6元,即买苹果的钱数-买2千克橘子的钱数=0.6元,列方程:7.4-2x=0.6,解方程,即可解答。
【详解】解:设每千克橘子x元,2千克橘子是2x元。
7.4-2x=0.6
7.4-2x+2x-0.6=0.6-0.6+2x
2x=7.4-0.6
2x=6.8
2x÷2=6.8÷2
x=3.4
答:每千克橘子3.4元。
8.(1)见详解
(2)9、10、16、17
【分析】(1)在日历中按图中框出的四个日期是在同一行或者同一列,同一行连续的四个数从左到右依次相差1,同一列的四个数从上到下依次相差7,框出的“田”字形的四个数中,已知左上角的数,则右边的数要加1,下方的数加7,右下方的数加8,据此可得出答案。
(2)可设第三种方法框出的四个数中左上角的数为x,则右边的数为x+1,下方的数为x+7,右下角的数为x+8,四个数相加等于52,解出方程,进而得出四个数。
【详解】(1)第一个图形第一个数x,则右边的数依次为:x+1,x+2,x+3;第二个图形中第一个数是x,则下方的数依次为:x+7,x+14,x+21;第三个图形中左上角数x,则右上角数为x+1,左下角的数为x+7,右下角的数为x+8。如图:
(2)解:设长方形框中的左上角的数为x,则另外3个数分别为:x+1、x+7、x+8,可列出方程:
x+(x+1)+(x+7)+(x+8)=52
4x+16=52
4x+16-16=52-16
4x=36
4x÷4=36÷4
x=9,即另外三个数分别为:10、16、17。
答:这4个数分别是9、10、16、17。
9.(1)“”表示羽绒服的销售情况;“”表示泳衣的销售情况
(2)220;270
(3)100;80;见详解
(4)见详解
【分析】(1)从图中可知:第一季度(1、2、3月),温度低,羽绒服销量高,泳衣销量低;第三季度(7、8、9月),温度高,羽绒服销量低,泳衣销量高,据此判断即可。
(2)分别求出前三个季度羽绒服和泳衣的销量之和即可。
(3)根据第四季度(10、11、12月)天气转冷,泳衣的销售数量可能会下降,羽绒服数量可能会上升。
(4)根据数据,将统计图补充完整即可。
【详解】
(1)“”表示羽绒服的销售情况;“”表示泳衣的销售情况。
(2)140+60+20=220(件)
40+80+150=270(件)
前三个季度一共销售羽绒服220件,泳衣270件。
(3)估计该商场第四季度大约会销售羽绒服100件,泳衣80件,理由是:到第四季度已进入冬季,所以羽绒服的销售量要比第三季度有所上升,估计销售量是100件;而泳衣的销售量一定比第三季度下降,估计销售量为80件(合理即可,答案不唯一)
(4)如图:
10.见详解
【分析】观察统计图可以发现:在3个月到12个月这个范围内,两种鱼的生长都呈上升趋势,且变化幅度较小;在12个月到15个月这个范围内,两种鱼生长的上升度都较大,生长迅速;在15个月以后,A种鱼的生长速度非常缓慢,B种鱼停止生长,捕捞出售这两种鱼的最佳时间应该是这两种鱼快速生长期停止之后,这样既可以避免提前捕捞造成单尾鱼的质量过轻,又可以避免延时捕捞造成饲料的浪费,据此解答。
【详解】这个渔场在15个月~18个月时捕捞出售这两种鱼比较合适;因为此时鱼生长慢。
11.(1)折线统计图见详解
(2)4;4
(3)精英队的成绩呈逐渐上升趋势;先锋队的成绩呈先上升后下降,再上升的不稳定趋势。
(4)我预测下一场比赛精英队获胜。
【分析】(1)根据统计表中的数据,分别找到精英队和先锋队在每一场比赛中的得分,直接在统计图中找到对应的位置,标出各个数据点,用直线将同一队伍的数据点依次连接起来,就得到了折线统计图。
(2)找出第一场比赛时的成绩,用先锋队的得分减去精英队的得分;找出第五场比赛时的成绩,用精英队的得分减去先锋队的得分。
(3)根据折线统计图的变化趋势解答即可。从折线统计图可以看出,精英队的成绩整体呈现上升的趋势;先锋队的成绩呈现先上升(第一场到第二场),再下降(第二场到第四场),后上升(第四场到第五场)的变化趋势。
(4)根据折线统计图变化趋势直接解答即可。根据两队的历史成绩和变化趋势,可以预测下一场比赛精英队可能会获胜,因为他们的成绩整体呈上升趋势,表现更稳定。
【详解】(1)根据分析,画图如下:
(2)50-46=4(分),55-51=4(分)
两个篮球队第一场比赛的成绩相差4分,第五场比赛的成绩相差4分。
(3)根据分析,精英队的成绩呈逐渐上升趋势;先锋队的成绩呈先上升后下降,再上升的不稳定趋势。
(4)我预测下一场两个篮球队的比赛结果是:精英队获胜,因为他们的成绩比较稳定,且呈上升趋势。
12.6分米;6块
【分析】把一块长方形木料截成若干块相同的正方形小木板且没有剩余,说明正方形小木板的边长是长、宽的公因数,求正方形小木板的最长边长,就是求长、宽的最大公因数;用分解质因数的方法求出长、宽的最大公因数,再分别求出长、宽各可以截几个,最后相乘就是能截的块数。
【详解】18=2×3×3
12=2×2×3
18和12的最大公因数是:2×3=6
即正方形小木板边长最大是6分米。
18÷6=3(个)
12÷6=2(个)
一共:3×2=6(块)
答:所截成的正方形小木板边长最大是6分米,能截成6块这样的小木板。
13.16人;10队
【分析】找一个数的因数的方法:列乘法算式找因数,按照从小到大的顺序,一组一组的写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数;分别求出96和64的因数,再求出96和64的公因数,找出小于20的最大公因数,即就是每队的人数,再用五年级和六年级人数和除以每队人数,即可解答。
【详解】96=1×96=2×48=3×32=4×24=6×16=8×12
96的因数有:1,2,3,4,6,8,12,16,24,32,48,96。
64=1×64=2×32=4×16=8×8
64的因数有:1,2,4,8,16,32,64。
96和64的公因数有:1,2,4,8,16,32。
小于20的最大公因数是16;每队最多16人。
(96+64)÷16
=160÷16
=10(队)
答:每队最多16人,共可以分10队。
14.6月1日
【分析】根据题意,李阿姨每工作2天休息一天,即李阿姨每3天休息一天;王阿姨每工作3天休息一天,即王阿姨每4天休息一天;那么她们同时在家休息的间隔天数是3和4的公倍数;先求出3和4的最小公倍数,再加上上一次她们同时在家休息的日期,即可求出下次两人同时在家休息的日期。
【详解】2+1=3(天)
3+1=4(天)
3和4的最小公倍数是:3×4=12
即每12天两人同时在家休息。
5月20日+12天=6月1日
答:下次两人同时在家休息是6月1日。
15.(1)12人
(2)男生3排;女生2排
【分析】(1)要使每排人数相同,而且每排人数尽可能多,每排人数应是36和24的最大公因数,计算36和24的最大公因数即可解答。
(2)分别用男生的人数和女生的人数除以每排的人数,据此解答。
【详解】(1)36=2×2×3×3
24=2×2×2×3
36和24的最大公因数是2×2×3=12。
答:要使每排人数相同,每排最多排12人。
(2)男生:36÷12=3(排)
女生:24÷12=2(排)
答:按上面的排法,男生要排3排,女生要排2排。
16.25本;箱;
【分析】根据平均分用除法计算,第一问用总本数除以班数,第二问用总箱数除以班数,第三问把图书总数看作单位“1”,根据分数的意义,把1平均分成12份,每份是。
【详解】(本)
(箱)
答:每班分到25本,每班分到箱,每班分得这些图书的。
17.
【分析】根据题意,把一个分数约分后得,分母与分子多3;原来分数的分母比分子多12,说明约分时分数的分子和分母同时除以4;那么把约分后的分数的分子、分母同时乘4,即可求出原来的分数。
【详解】10-7=3
12÷3=4
=
答:这个分数是。
18.;;
李阳;过程见详解
【分析】先用每人射中次数除以射门次数,求出每人射中次数占射门次数的几分之几,据此填表;再根据分数大小比较的方法进行比较,得出谁射门最准。
分数大小的比较:
分母相同时,分子越大,分数值就越大;
分子相同时,分母越大,分数值反而越小;
分子、分母都不相同时,利用分数的基本性质化成同分母或同分子的分数进行比较。
【详解】李阳:3÷5=
刘明:4÷7=
张扬:5÷9=
填表如下:
姓名 李阳 刘明 张扬
射门次数 5 7 9
射中次数 3 4 5
射中次数占射门次数的几分之几
==
==
==
>>
即>>。
答:李阳射门最准。
19.;
【分析】分子和分母的公因数只有1的分数叫最简分数。如果一个最简分数的分母是分子的6倍,则分母是分子的倍数,但它们的公因数只有1,那么分数的分子是1,分母是6,据此写出分数;
分数的分母是分子的6倍,分子与分母相差20,根据差倍问题中“较小数=差÷(倍数-1)”,用20除以(6-1)即可求出分子,用分子乘6求出分母。
【详解】一个分数的分母是分子的6倍,这个分数写成最简分数是;
分子:20÷(6-1)
=20÷5
=4
分母:4×6=24
则这个分数是。
20.吨
【分析】用西瓜的总重量减去第一天卖出西瓜的重量,减去第二天卖出西瓜的重量,即可求出剩下的重量。
【详解】--
=--
=-
=(吨)
答:还剩吨。
21.吨
【分析】用第一周用去大米的重量-,求出第二周用去大米的重量,再把两周用去大米的重量相加,即可解答。
【详解】-+
=-+
=+
=(吨)
答:两周一共用去吨大米。
22.
【分析】把暑假出行去旅游的总人数看作单位“1”,用单位“1”分别减去去北京的占总人数的和去海南岛的占总人数的,所得差即为去黄山旅游的占总人数的几分之几。
【详解】
答:去黄山旅游的占总人数的。
23.分米
【分析】先要判断等腰三角形的腰和底的长各是多少分米,根据三角形的两边之和大于第三条边,两边之差小于第三条边求出另一条边的长度,最后求出三条边的长度之和就是这个等腰三角形的周长,据此解答。
【详解】①当分米为等腰三角形的腰时
(分米)
(分米)
因为,所以等腰三角形的三条边的长度分别是分米、分米和分米。
当分米为等腰三角形的腰时
(分米)
因为,所以分米、分米和分米不能组成三角形。
(分米)
答:这个等腰三角形的周长是分米。
24.
【分析】“天舟六号”飞船图片比“神舟十五号”飞船图片少占总数的,“神舟十五号”飞船图片占总数的分率=“天舟六号”飞船图片占总数的分率-,最后再加上“神舟十五号”飞船图片占总数的分率。
在分数的计算过程中,先同分母分数相加,然后异分母分数相加转化为同分母分数相加即可。
【详解】
=
答:他收集的“天舟六号”和“神舟十五号”飞船图片的数量占总数的。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
